基于集值统计的招标采购综合评标方法研究

高翠娟，孟凡奇，张　桦，张敏芳（.军械工程学院装备指挥与管理系，河北石家庄050003；.总装备部通用装备保障部，北京000）

基于集值统计的招标采购综合评标方法研究

高翠娟1，孟凡奇2，张桦1，张敏芳1
（1.军械工程学院装备指挥与管理系，河北石家庄050003；2.总装备部通用装备保障部，北京100120）

针对通装维修器材设备招标采购评标方法单一、综合评标方法主观性强的问题，借用集值统计技术方法对招标采购综合评标数据进行区间模糊处理，建立基于集值统计的综合评标模型，对专家的综合评分进行统计处理，降低专家评分的主观性，确保综合评分的科学性。最后通过对该方法在某器材招标采购过程中的应用，充分证明其适用性。

集值统计；招标采购；综合评标

招标采购因在采购活动中促进供应商展开竞争而提高采购效益，因而被广泛推广。评标是招标采购的关键环节，其中综合评标法是一种根据约定的比重加权以后得出评分结果，并以此作为定标依据进行评标的一种方法。与有限低价法相比具有更科学、更量化的优点，因而是最常用的一种评标方法。但综合评标方法也是专家作用最突出的一种方法，较为依赖专家的主观评分。鉴于综合评标方法应用较为广泛，但主观性较强的问题，本研究试借用集值统计技术对综合评标过程予以改进，建立综合评标方法模型，通过计算得到合理分值，提高综合评标可信度。

1　集值统计指标处理

由汪培庄教授提出来的集值统计方法［1］是在经典的概率统计中，通过将每次试验相空间中确定的点范围拓宽，使得每次试验所得可以是相空间的一个模糊子集，从而体现人思维的模糊处理。集值统计是经典统计和模糊统计的一种推广，应用时相当于专家对某项评价指标给出的是一个区间估计值，该统计方法为主观评价提供了一种新的定量化手段。

1.1对单因素评价值的统计处理［2-3］

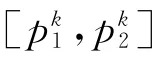
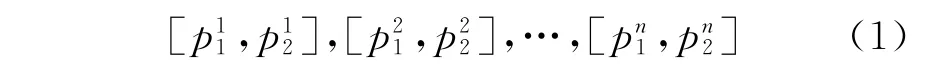
将这n个区间评分值叠加在一起即形成覆盖在评标得分数值轴上的一种评分分布，可用下式描述

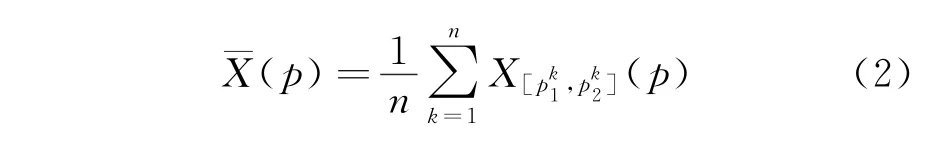
该式表示评分数值的模糊覆盖频率，也即p值的落影函数。其中：

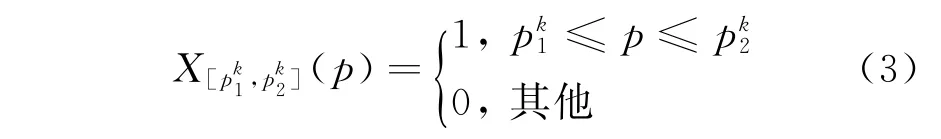
假设对某项评价指标的评分最小值为pmin，最大值为pmax，则该项评价指标的最终评分值为

则有

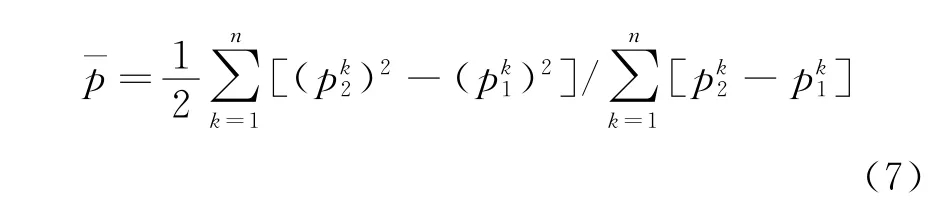
极端情况下，所有专家均认同一种观点，即对该项评价指标评分的情况下，对所有k…=c（常数），该项评价指标评分数值为¯p=c。

1.2评标结果的可信度评价

依统计原理推断，假如所有专家的评分值在数值轴上的分布比较集中，则说明各专家对该评价指标的评分比较统一，相对可信度较高。反之，如果所有专家的评分值在数值轴上的分布较为分散，则说明各专家对该评价指标的评分不统一，可信度低，需要请专家重新评价后再评分。若专家对某风险因素发生概率的估计值区间叠加后所形成的频率覆盖的落影离散程度为g，则有：

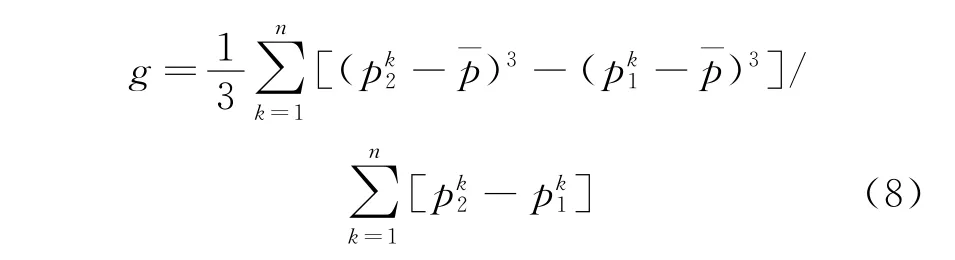
可以证明，若离散度g越小，专家评分数值的可信度越高，也即专家对该项评价指标的评分值越能反映实际情况，主观性越小。运用集值统计方法可以客观处理专家评分信息，从而减少专家打分过程中的随机误差，使评分值的结果更加科学合理。

2　基于集值统计的综合评标方法［4-8］

2.1评标标准

在评标方法中进行具体应用时，须先列出具体的评分因素层级结构，并给出每项评分因素的评分参考范围，使得专家评分在一个平台上进行，评分结果更为客观可信，本研究就一级评分因素进行讨论。

2.2单因素评价

在评标标准的基础上，请专家根据评分数值的参考范围说明对每一项评分因素给出一个大致的评分范围，进而应用集值统计方法对数据进行处理，以期得到相对客观的评分分值。以产品采用标准和贯彻标准情况（简称“采标”“贯标”）评标标准为例，评分值的参考范围如表1所示。

表1　评分数值的参考范围

2.3评标结果计算

针对每项评分因素的评分数值，直接采用上文推导公式，即首先用式（7）计算得出各专家对该项评分因素的评分结果，进而需要通过离散度g的计算，即式（8）进行可信度检验。

3　应用实例

3.1案例背景

假设须对某器材实施招标采购，经论证，拟在评标过程中采用综合评标方法，为降低专家评分过程中的主观模糊性，评分数值拟采用集值统计综合评标方法。在评标过程中，我们除了常用的有限低价法等评标方法外，还可以采用此种基于集值统计的综合评标方法进行评标。通过分析，确定该器材采购的评分因素分别为：性能指标、满足需求程度、报价合理性、售后服务、技术先进性、质保体系、企业资质等7个方面，如表2所示。

表2　评标指标

3.2专家打分［9-10］

假设该招标采购项目邀请5位专家，按照集值统计方法进行评分。经过评标，5位专家对某投标企业的7项评分因素的评分区间如表3所示。其中评分数值均为区间估计值，以最大限度反映专家评分的思维模式，表示专家最客观的评分判断，使评标分析的结果趋于真实、科学。

表3　专家评分数值表

3.3综合计算

对表3的评分数据进行集值统计计算，根据上文提出的评分值的计算方法，按式（7）计算每一个评分因素的综合评标分值，最终计算结果如表4所示。

表4　某维修器材采购评标专家评分数值

进而经过可信性检验，对每一评分因素估计数值，即每一行数据按式（8）计算离散度。经计算，该次评分结果数据的值均较小，说明在对该通用装备维修器材招标采购中，各位专家对评标的各项评分因素评价值比较集中，数据是可信的，评分结果可用。

4　结束语

招标采购能否发挥效益，关键在评标方法的科学运用，如何利用现有评标方法解决好采购问题值得我们深思。本文在综合评标方法研究过程中，根据具体情况，研究基于集值统计的综合评标方法，对专家评分进行区间化模糊处理，降低了专家赋值的主观性，提高了评分的准确度和科学性，能够更好地解决招标采购中的评标问题。

（References）

［1］汪培庄.模糊集与模糊集落影［M］.北京：北京师范大学出版社，1985：60-65.

［2］秦寿康.综合评价原理与应用［M］.北京：电力工业出版社，2003：17-19.

［3］全国人民代表大会常务委员会.中华人民共和国政府采购法［M］.北京：法律出版社，2002：4-5.

［4］国家计委，国家经贸委，建设部，铁道部，交通部，信息产业部，水利部.评标委员会和评标方法暂行规定［M］.北京：人民法院出版社，2001：1-3.

［5］财政部.政府采购货物和服务招标投标管理办法［M］.北京：人民法院出版社，2004：2-4.

［6］张冰心.现行评标方法的适应性分析［J］.商场现代化，2010（7）：69-70.

［7］全国人民代表大会常务委员会.中华人民共和国招标投标法［M］.北京：中国标准出版社，1999：2.

［8］崔建宁.采购招标评标方法的探究［J］.建筑监督检测与造价，2011（10）：66-69.

［9］徐佳.基于模糊评价的工程项目评标方法研究［J］.烟台职业学院学报，2013（1）：66-71.

［10］李鸿吉.模糊数学基础及实用算法［M］.北京：科学出版社，2005：309-351.

（编辑：田丽韫）

加

Research on Competitive Acquisition Comprehensive Bid Evaluation Method Based on Set-Value Statistics

GAO Cuijuan1，MENG Fanqi2，ZHANG Hua1，ZHANG Minfang1
（
1.Department of Equipmen Command and Admimistration，Academy of Ordnance Engineering，Shijiazhuang Hebei 050003，China；
2.General-purpose Equipment Support Department，General Armament Headquarters，Beijing 100120，China）

The method of evaluating the bids for general equipment maintenance material acquisition is single and subjective，so it is necessary to conduct interval fuzzy processing for evaluated data with set-value statistics，establish a comprehensive evaluation model based on this method，statistically process the comprehensive evaluations of the experts and reduce the subjectivity of evaluation by experts in order to ensure scientific comprehensive evaluation.In the end，the paper fully demonstrates the applicability of the method by introducing its application in an equipment project competitive acquisition.

set-value statistics；competitive acquisition；comprehensive bid evaluation

TP91

2095-3828（2015）02-0036-03

ADOI 10.3783/j.issn.2095-3828.2015.02.009

2014-01-01

高翠娟（1979-），女，讲师，硕士，主要研究方向为装备采购管理。karen_gaocj@163.com