油气管道腐蚀缺陷分类识别技术研究

朱红秀，刘 欢，李宏远，黄松岭，苏志毅

（1.中国矿业大学（北京）机电与信息工程学院，北京 100083；2.清华大学电机系电力系统国家重点实验室，北京 100084）

0 引 言

目前，漏磁检测已成为国内外最有效的油气管道缺陷检测方法之一，然而难以定量的特点阻碍了其进一步向自动化、智能化方向发展[1]。量化困难的原因在于缺陷种类繁多，而每一种缺陷的形态又对漏磁场的形态有着复杂的非线性影响，任何单一的数学模型或者统计模型都不可能绝对准确。因此，若要实现对多种缺陷的准确量化，根据缺陷的形状特征对其进行智能分类是必不可少的[2-3]。国外的Lord最早将有限元引入到漏磁数据分析中；Ameet Joshi等[4]提出一种基于小波基神经网络的缺陷三维重构算法，取得了一定效果。国内不少学者也致力于此方面研究，崔伟[5]建立了RBF神经网络作为正问题的求解模型并利用迭代法对缺陷进行定量分析；田凯等[6]提出使用贝叶斯算法BP神经网络用于缺陷的评估识别；上述技术在量化算法上不断完善，但往往忽略前期分类的重要性，对其阐述不多。即便是在缺陷分类中已有应用的神经网络，由于其自身算法的局限性，也难以保证分类的准确度和效率，在非常讲究时间的实际工程中，这是不明智的。

为改善这一现状，本文从缺陷的形状参数对漏磁信号的影响入手，特别引入工程中常见的多缺陷聚集时的影响因素，建立一种基于BP神经网络[7]的新型缺陷分类器。针对油气管道的特点，改进传统Levenberg-Marquardt（LM）算法精度低、效率差、收敛条件要求苛刻的弊端；并利用Ansoft Maxwell 3D仿真缺陷数据对网络进行测试[8]，加以验证。

1 缺陷漏磁信号特征分析

首先，利用Ansoft Maxwell 3D软件仿真缺陷漏磁场建立一个标准缺陷数据库，分析缺陷外形参数和漏磁场信号之间的关系。

1.1 缺陷长度对漏磁信号的影响

图1为宽度1T，深度0.5T，长度分别为1T，2T，…，7T的7个长方体缺陷的漏磁信号。

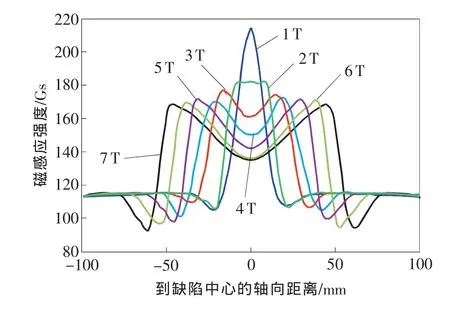
图1 缺陷长度对漏磁信号的影响

从图中可以看出，随着长度的增加，信号强度逐渐下降，但并非呈反比例关系，而是随长度增大到一定程度后渐趋稳定。同时，信号向两端靠近，中间形成凹陷。

1.2 缺陷宽度对漏磁信号的影响

图2对比了长为1T、宽为3T以及长为3T、宽为1T，深度均为0.5T的两个缺陷的漏磁信号。

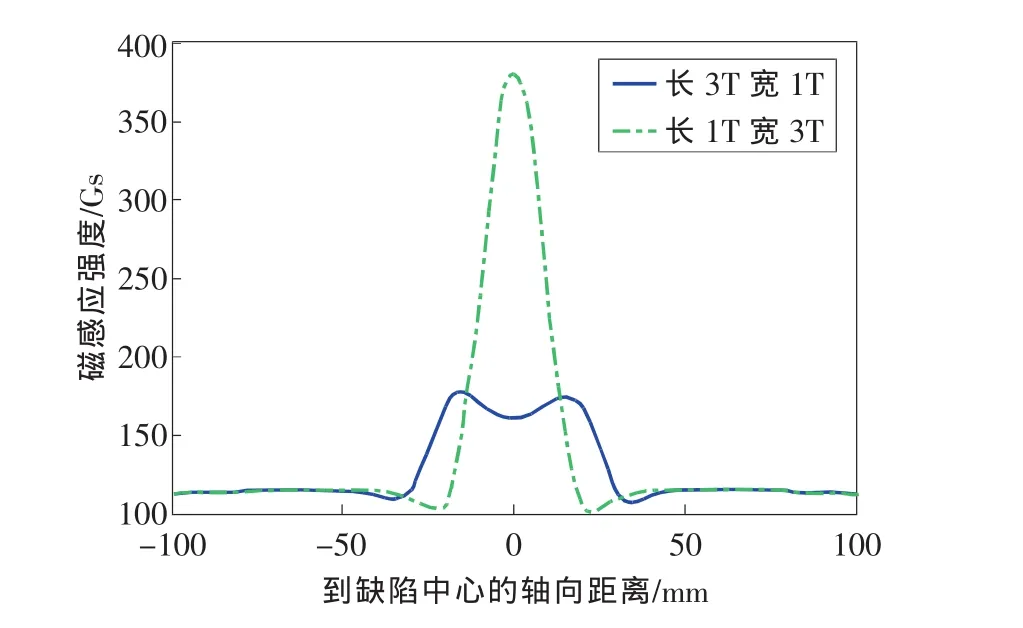
图2 宽长比分别为3∶1和1∶3的两个凹槽缺陷漏磁场对比

两者的峰谷值相差非常大，与宽长比成正相关。达到一定程度后，峰谷值渐趋稳定。据观察，宽长比在 3∶1～1∶3之间时，峰谷值变化受影响最为明显。

1.3 缺陷深度对漏磁信号的影响

图3是开口为1T×1T的正方形缺陷深度在0.2~0.7T间变化时的漏磁信号。

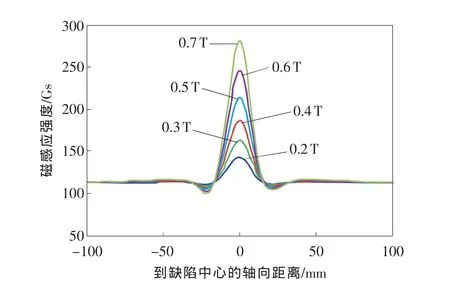
图3 长1T宽1T的缺陷漏磁场随缺陷深度变化

对于相同开口形状的缺陷，峰谷值几乎与缺陷深度成线性正相关，线性系数随开口形状而变化。

1.4 多缺陷聚集对漏磁信号的影响

在实际的油气管道腐蚀中，更为常见的其实是多个腐蚀缺陷相距较近，漏磁场相互影响的形态，有两种情况：当缺陷沿轴向并列分布且相互靠近时，会使漏磁场区域的峰谷值减小；当缺陷沿周向并列分布且相互靠近时，会使漏磁场区域的峰谷值增大。

2 漏磁信号特征提取

相似的漏磁信号可能对应两个截然不同的缺陷，本文以轴向凹槽和轴向并列针孔为例，设计基于改进BP神经网络的缺陷分类算法。该算法的输入是缺陷漏磁信号的特征量，输出是缺陷根据形状的分类结果。如图4所示，对漏磁信号提取以下特征量：

1）峰谷值 YP-P，Gs。

2）谷谷间距 XP-P，mm。

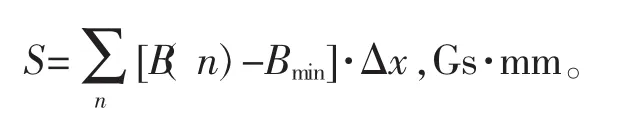
5）一次差分峰谷间距 XDP-P，mm。

6）一次差分峰谷值 YDP-P，Gs/mm。

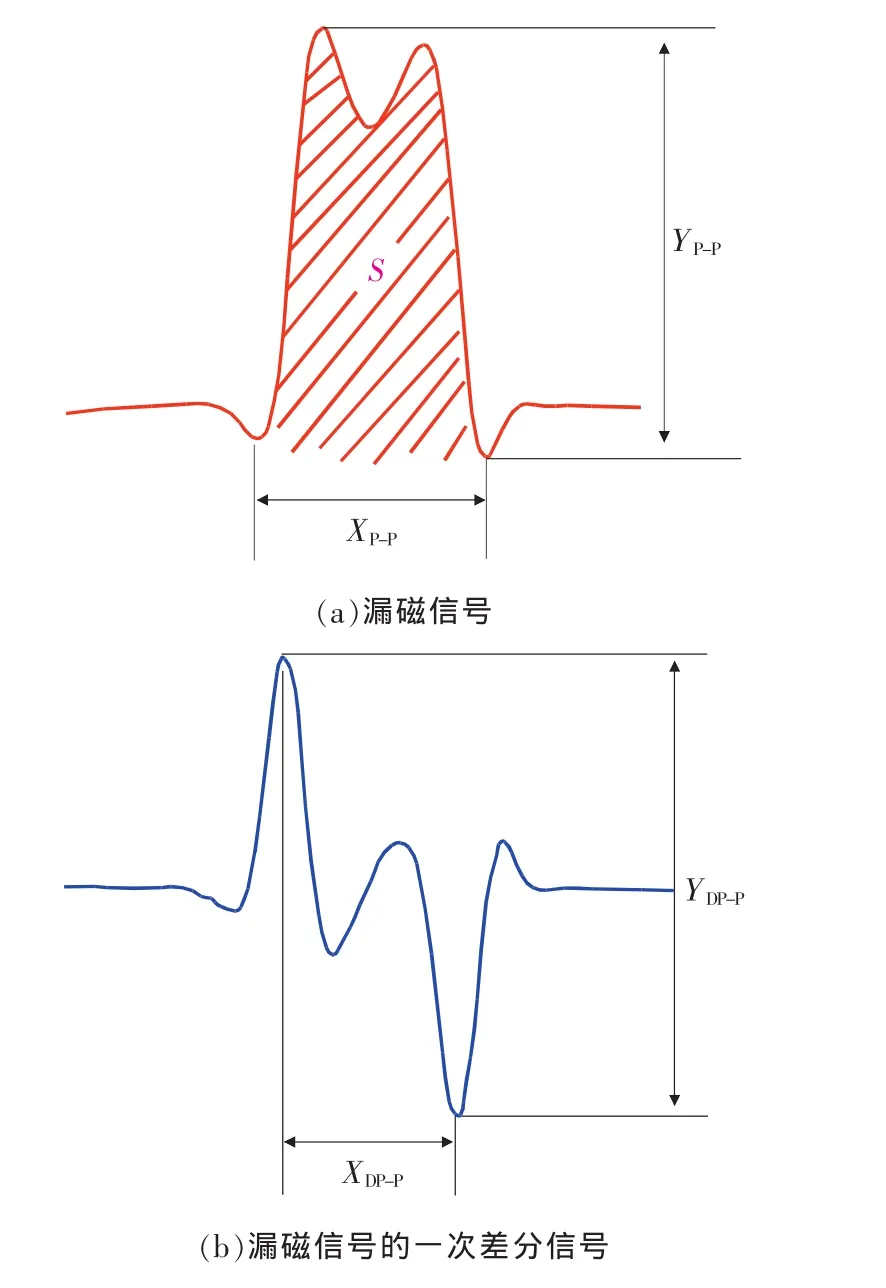
图4 漏磁场信号特征量说明

3 改进LM算法的全局收敛BP神经网络

BP神经网络是基于误差反向传播算法的多层前馈神经网络。图5为一个典型的多层前馈网络的结构模型。

输入层、隐层和输出层分别有P、M、N个节点，IW和LW分别表示输入到第一个隐层的权重矩阵和后面神经元层间的权重矩阵。针对缺陷分类设计的BP神经网络，其输入p为一个6维向量，分别表示6个特征量（归一化的）；输出为标量，不失一般性，这里使输出y=-1时表示“轴向凹槽”，输出y=1时表示“轴向并列针孔”；隐层和输出层的神经元均采用Sigmoid函数。

图5 具有一个隐层的前馈网络结构

牛顿法是一种广泛使用的求解非线性方程组的迭代算法，训练样本中网络输出和理想输出之差为

式中x为权重和阈值向量。E可以考虑为F（x）评价函数。每次迭代中要计算一个牛顿步：

式中：k——当前迭代次数；

N——牛顿法；

Fk=F（ xk）；

Jk=F′（xk）——Jacobi矩阵。

当J（x）在解处满足Lipschitz条件且矩阵非奇异时，牛顿法二次收敛。但在神经网络的训练中，无法保证Jacobi矩阵非奇异。为克服此困难，Levenberg-Marquardt（LM）算法提出另一种新算法：

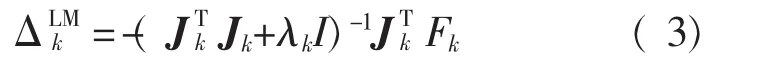
其中，LM系数λk＞0在每次迭代中更新。很显然，当Jk非奇异且λk接近于0时，式（2）变成接近式（1）的形式，高速向极小值处靠近；若Jk接近奇异，则增大λk的值，这时式（2）更接近小步长的梯度下降法。但是，LM算法的收敛性依然需要Jacobi矩阵在解处保证Lipschitz连续且非奇异，但这个条件太强，不易实现。

针对以上两种算法存在的问题，本文提出利用以下改进的算法对BP神经网络进行训练：

1）给定x1（如需要修改的对象为权重向量x=LW2，1则 x1∈RM），ε＞0，α1＞τ＞0，0＜p0＜p1＜p2＜1，使 k=1。

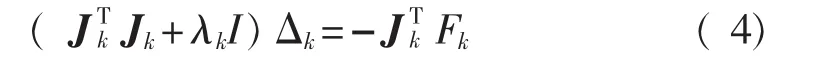
3）计算F（x）的实际下降量Aredk和估计下降量Predk以及这两者的比值，即：

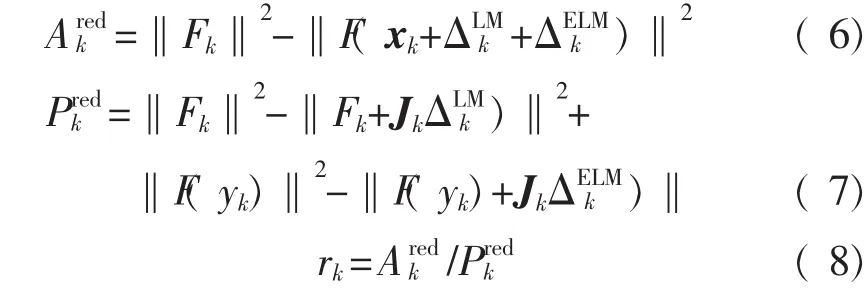
如果 rk≥p0，则 xk+1=xk+sk；否则，使 xk+1=xk。

4）按下式计算，即：

并使 k=k+1，再返回 2）。

本文提出的改进LM算法有如下3个特点：

1） 用 Jk代替了 J（ yk），只需要计算 F（ yk）就可以迅速求得估计LM步，大大减小了计算量。

2）由于使用了估计LM步，不能保证传统定义下的估计下降量（ ‖Fk‖2-‖Fk+Jksk‖2）满足非负条件，但这个性质对于算法的全局收敛性是非常必要的。因此，定义使用了新的估计下降量Predk，如式（7）所示，解决了这个问题。

3）改进LM算法在某程度上可以考虑为一种信赖域算法，而不是线搜索方法，即通过求解某个模型直接得到试探步，而不是先确定搜索方向，再计算步长。具体来说，可以通过评价函数rk确定是否接受试探步，如果评价好，就接受；如果评价不好，就不接受；从而决定在下一次迭代中是保持、增大还是减小信赖域的半径。这样既保证精度又不失灵活性，效率得到了提高。

4 分类网络训练与测试

使用Ansoft Maxwell 3D对轴向凹槽和轴向并列针孔分别仿真计算了一系列外形参数下的漏磁信号，一部分作为训练样本，一部分作为测试样本。

4.1 训练效果对比

为方便对比，使用Matlab工具箱自带的BP模型对训练样本集进行训练，属性分为“traingd”和“trainlm”，即梯度下降法和经典LM算法。

对于改进 LM 算法，可以设定参数 ε=1×10-5，τ=1×10-8，p0=0.0001，p1=0.25，p2=0.75。 对于所有网络，隐层节点数为15，训练达到准确度目标或者迭代次数超过500，则停止训练。

3种网络的对比训练过程如图6所示。对比分析图 6（ a）、图 6（ b）和图 6（ c），可以看出：

1）梯度下降算法收敛速度非常缓慢，达到上限迭代次数后准确度只有0.734，不满足要求。

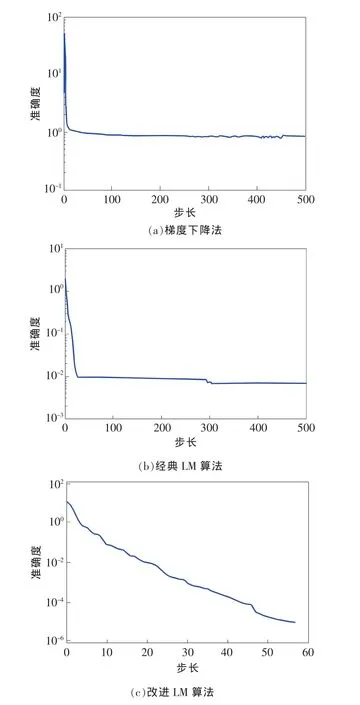
图6 3种分类神经网络对比训练过程

2）经典LM算法收敛速度比较快，但准确度到达1×10-2和1×10-3之间时开始停滞，似乎陷入了局部最小点，不满足要求。

3）改进LM算法收敛速度非常好，迭代次数也大幅度减少，仅仅经过57次迭代后就顺利达到了目标精度，不但满足要求，而且节省了大量时间。

4.2 测试效果对比

对3种网络进行测试，输出如表1、表2所示。第1行表示期望的网络输出，“-1”表示轴向凹槽，“1”表示轴向并列针孔；第2行“GD”表示该BP神经网络使用梯度下降法进行训练；第3行“LM”表示网络使用经典LM算法进行训练；第4行“MLM”表示网络使用改进LM算法进行训练。对比分析可以看出：

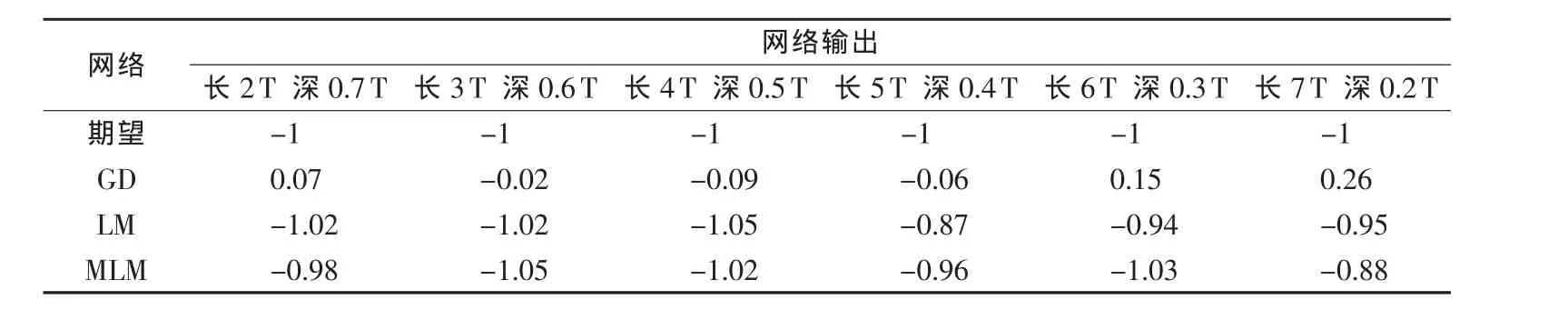
表1 轴向凹槽的分类测试结果

表2 轴向并列针孔的分类测试结果

1）梯度下降算法测试结果不理想，与期望值相差较大，不足以作为分类参考，可以忽略。

2）经典LM算法测试结果比较理想，虽然没有达到目标精度，但对于所有测试样本，最大的输出误差不超过1-0.75=0.25，也勉强可以接受。但在训练速度上，效果一般。

3）改进LM算法测试效果非常理想，顺利达到目标精度，输出误差也满足要求。特别强调的是，全局收敛的改进LM算法在训练速度上有着明显的优势，优于梯度下降法和经典LM算法。对于更加复杂的网络结构，或更大规模的训练样本集，快速收敛是非常有必要的，从某种角度讲，甚至可以作为算法是否适合工程使用的一个标准。

5 结束语

设计并建立一种基于改进BP神经网络模型，用于油气管道腐蚀缺陷分类识别，并以轴向凹槽和轴向并列针孔数据为例进行训练和测试。结果表明：本方法效果良好，训练速度明显快于普通BP神经网络，量化误差满足实际要求，并且在保证目标精度的情况下，迭代次数少，又能迅速收敛，较好地改善了当前分类算法中存在的缺点与不足。该方法已成功应用于胜利油田软件工程项目当中，是国内自主研发产品的第一次实际应用，经多次现场实验，运行平稳，不仅提高了效率，同时也节省了成本。在此基础上，如何发掘更科学有效的算法，实现对管道缺陷的准确量化，是下一步的研究目标。

[1]黄辉，何仁洋，熊昌胜，等.漏磁检测技术在管道检测中的应用及影响因素分析[J].管道技术与设备，2010（3）：17-19.

[2]吴欣怡，赵伟，黄松岭.基于漏磁检测的缺陷量化方法[J].电测与仪表，2008，45（ 5）：20-22.

[3]黄松岭，李路明，鲍晓宇，等.管道漏磁检测中的信号处理[J].无损检测，2000（ 2）：55-57.

[4]Joshi A， Udpa L， Udpa S， et al.Adaptive wavelets for characterizing magnetic flux leakage signals from pipeline inspection[J].Magnetics IEEE Transactions，2006，42（ 10）：3168-3170.

[5]崔伟，黄松岭，赵伟.基于RBF网络的漏磁检测缺陷定量分析方法[J].清华大学学报：自然科学版，2006（ 7）：1216-1218.

[6]田凯，孙永泰，高慧，等.贝叶斯算法BP神经网络缺陷量化研究[J].中国测试，2014（ 3）：93-97.

[7]吴欣怡，黄松岭，赵伟.使用改进型BP神经网络量化裂纹漏磁信号[J].无损检测，2009（ 8）：603-605.

[8]Fan J.The modified Levenberg-Marquardt method for nonlinear equations with cubic convergence[J].Mathematics of Computation，2012，81（ 277）：447-466.