环形磁钢空心杯电机空载漏磁系数的计算

2022-10-15袁永杰郑文鹏魏学鹏赵金磊李立娜

微特电机 2022年9期

袁永杰，郑文鹏，魏学鹏，赵金磊，李立娜

(1.中国电子科技集团公司第二十一研究所，上海 200233；2.西安现代控制技术研究所，西安 710065)

0 引言

空心杯电机及其组件具有体积小、效率高、响应快、无齿槽转矩、运行平稳等优点，近年来作为伺服驱动元件在自动化装备和伺服系统中有着广泛的应用。空心杯电机的工作原理与普通永磁直流伺服电动机相同，即为通电导体在永磁体形成的磁场内受力旋转。不同之处在于，空心杯电机的绕组不放置在冲片槽内，而仅仅使用漆包线绕制而成，因此空心杯电机的气隙长度远大于一般电机；另外其磁钢采用环形磁钢，其磁路结构有着特殊性，一般的磁路计算中漏磁系数通过经验选取并不合适，直接影响到磁路计算的准确性。

文献[1]介绍了漏磁系数的几种计算方法，但没有介绍解析计算方法。文献[2]分析了环形磁钢的漏磁系数，但只分析了极间漏磁和齿顶漏磁，没有分析端部漏磁。文献[3]介绍了内置式永磁体的无刷电机的漏磁系数，并给出了解析表达式，但其解析结果与有限元结果有一定差异。

本文对环形空心杯电机的磁路进行分析，并给出了磁路模型。根据模型列出了空载漏磁系数(以下简称漏磁系数)的解析表达式。并针对两款不同机座号的电机进行了计算，计算结果与磁力线法、磁矢位法两种常用的有限元方法的计算结果相吻合，验证了解析表达式的正确性，为环形磁钢空心杯电机的磁路准确计算提供参考。

1 环形磁钢空心杯电机漏磁系数解析表达式

环形铁心空心杯电机的基本电磁结构如图1所示，分为永磁体、电枢杯绕组和机壳三部分，三部分同轴，有刷空心杯电机电枢杯旋转，无刷空心杯电机永磁体旋转。机壳与永磁体之间的气隙称为总气隙，转子杯与永磁体之间的气隙称为内气隙，转子杯与机壳之间的气隙称为外气隙。

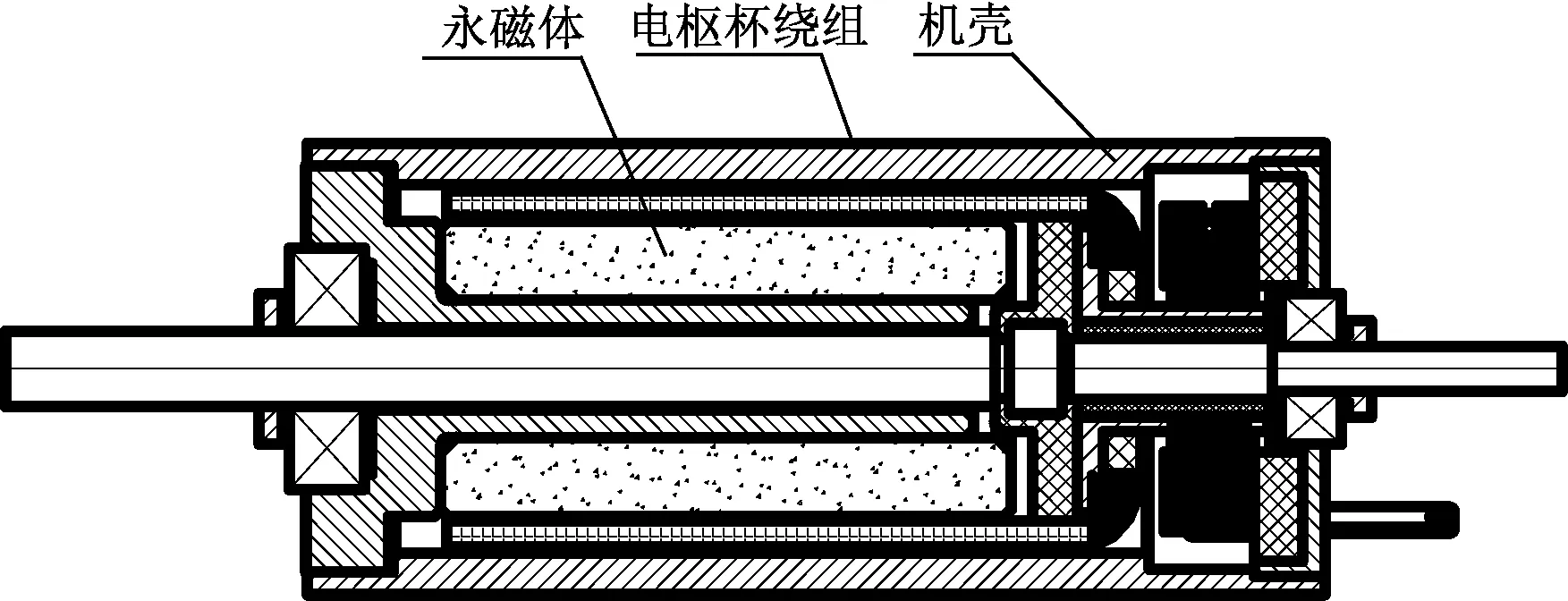
图1 环形磁钢空心杯电机磁路结构图

永磁体发出的全部磁通称为总磁通Φ0，总磁通中大部分与电枢绕组交链，称为主磁通Φm；少部分通过极间、端部等位置闭合而不与电枢绕组交链，称为漏磁通Φσ。漏磁系数σ即为总磁通与主磁通的比值：

(1)

式中：Φσ1为极间漏磁通；Φσ2为端部漏磁通。

忽略机壳磁阻，建立等效磁路图如图2所示。图2中Λm为永磁体磁导，Λδ为气隙磁导，Λσ1为极间漏磁导，Λσ2为端部漏磁导。

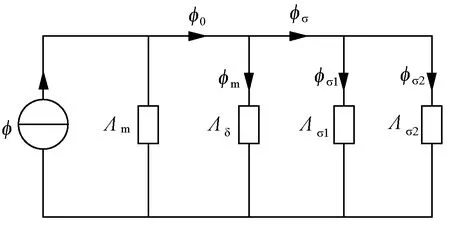
图2 空心杯电机等效磁路图

按磁导定义计算各部分磁导[4]。

气隙磁导：

(2)

式中：μ0为空气磁导率；τ为极距；Lef为计算电枢长度。

极间漏磁示意图如图3所示，虽然空心杯电机的实际气隙比普通齿槽电机大，但由于电枢绕组与磁极体间的内气隙较小，因此只要与整个电枢绕组交链的磁通均为主磁通，极间漏磁主要是在内气隙间形成磁回路，不与电枢绕组交链磁通。极间漏磁导：

(3)

式中：δ为气隙高度；LM为磁钢轴向长度；Dout为磁钢外径。

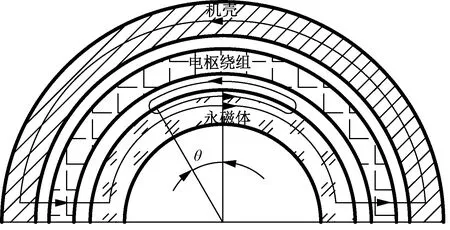
图3 空心杯电机主磁通和极间漏磁通

端部漏磁磁路主要是由半径为x的两段圆弧和一段直线组成，端部漏磁导Λσ2：

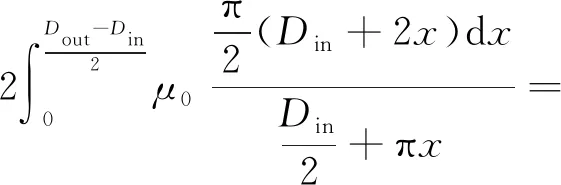
(4)

式中：Din为磁钢内径。

端部漏磁示意图如图4所示。

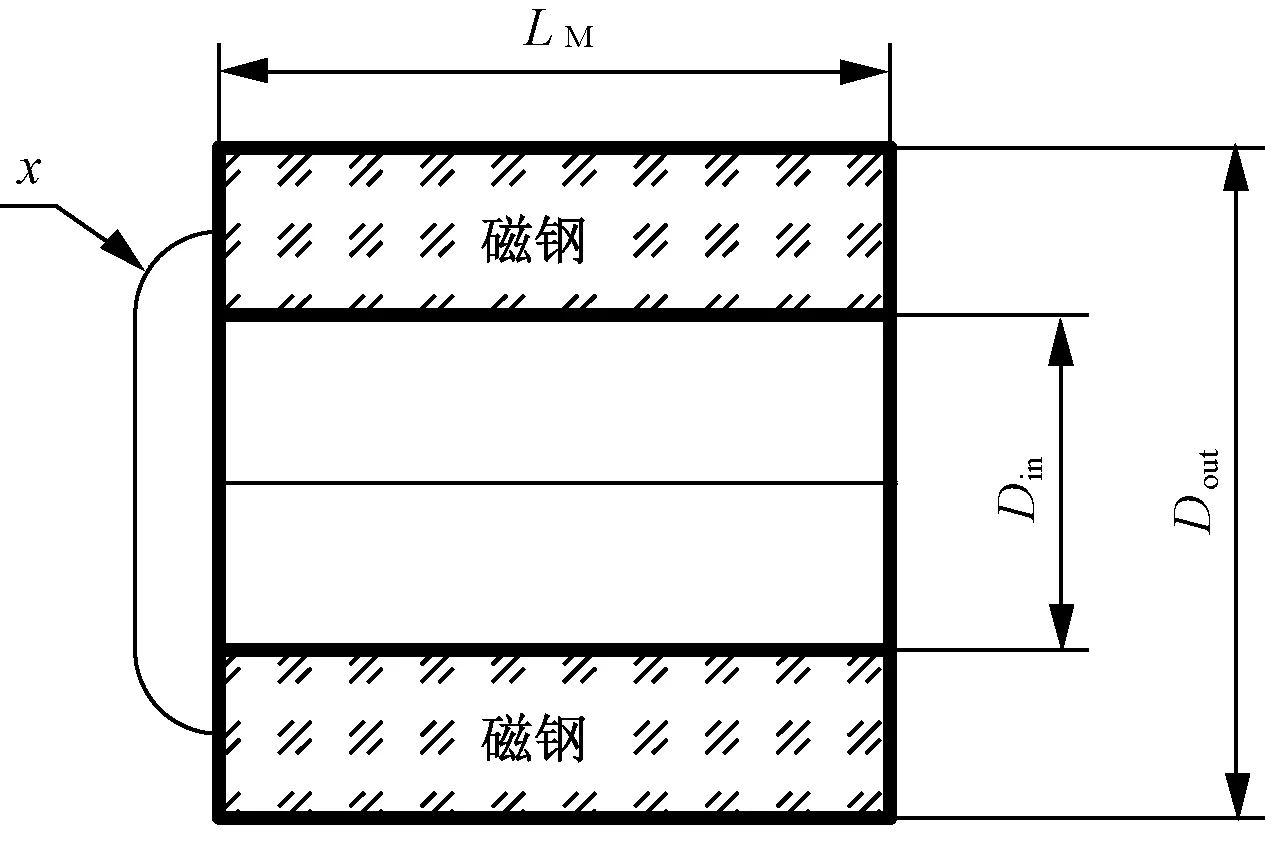
图4 端部漏磁示意图

磁通与磁导成比例，可以得出漏磁系数如下：

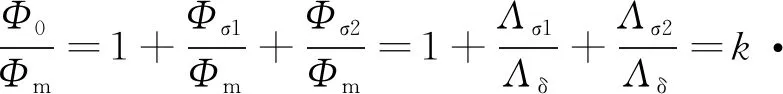
(5)

式中：k为经验校正系数。

以电机1(外径30 mm)的空心杯电机为例，极数2p=2；磁钢内径Din=9.1 mm；磁钢外径Dout=19.7 mm；磁钢轴向长度LM=35 mm；总气隙δ=2.5 mm；计算电枢长度Lef=38 mm。按照漏磁系数解析表达式计算得σ=1.128k。

下面通过磁矢位法和磁力线法计算校正系数k。

2 磁矢位法计算漏磁系数

磁矢位法求解漏磁系数同样分为极间漏磁和端部漏磁两部分[5]，极间漏磁的求解模型如图5所示。

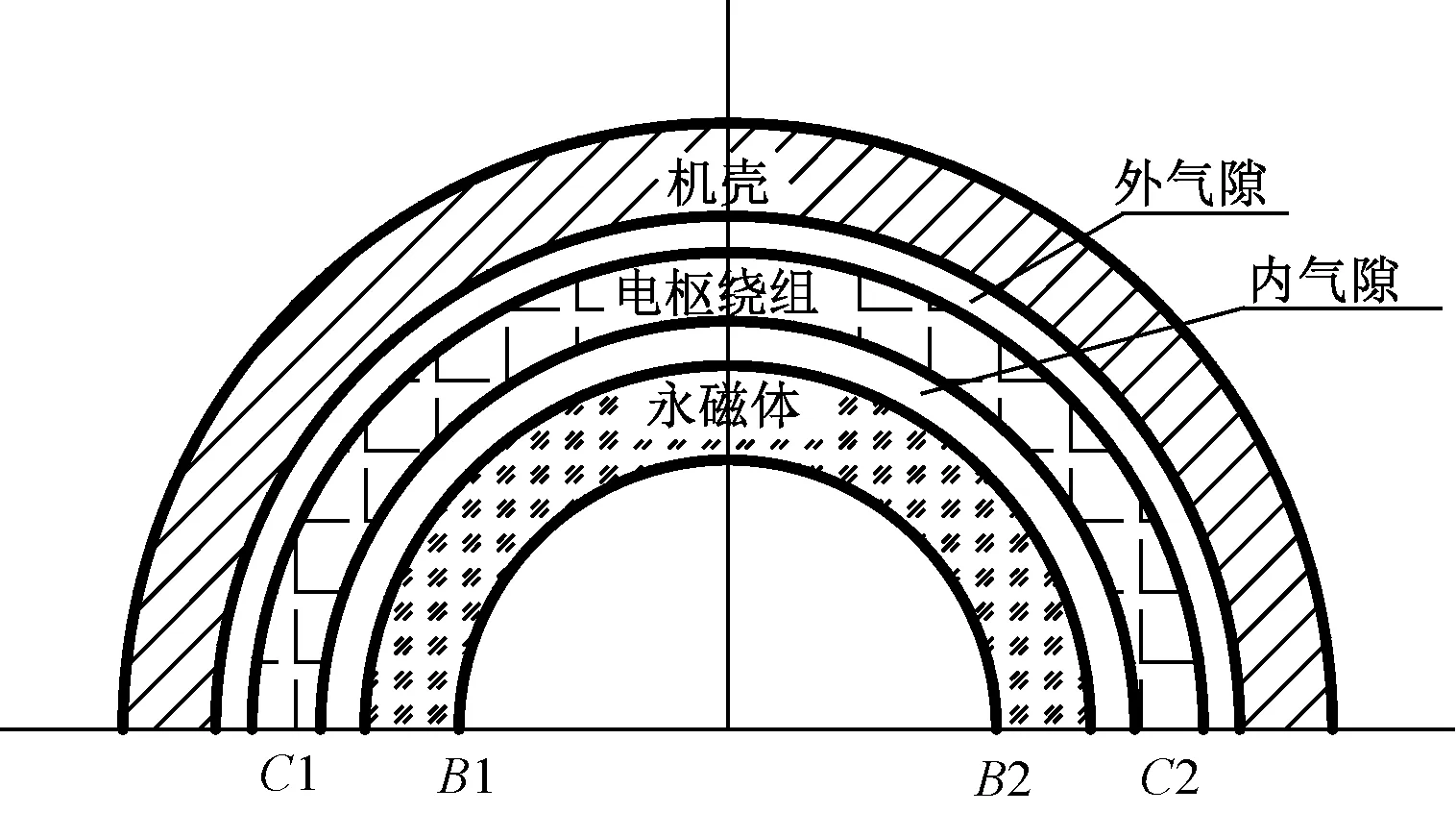
图5 磁矢位法计算极间漏磁模型

(6)

式中：Ω为求解场域；L为模拟永磁体等效面电流边界；Js为模拟永磁体的等效面电流密度，法线n从永磁体指向外部；Γ1为第一类齐次边界。

通过磁场计算，可以得到场域中各点的磁矢位，则可以计算得出极间漏磁系数：

(7)

端部漏磁模型如图6所示，端部漏磁系数采用同样的方法计算。计算模型如图7所示，计算结果如图8、图9所示。

(8)

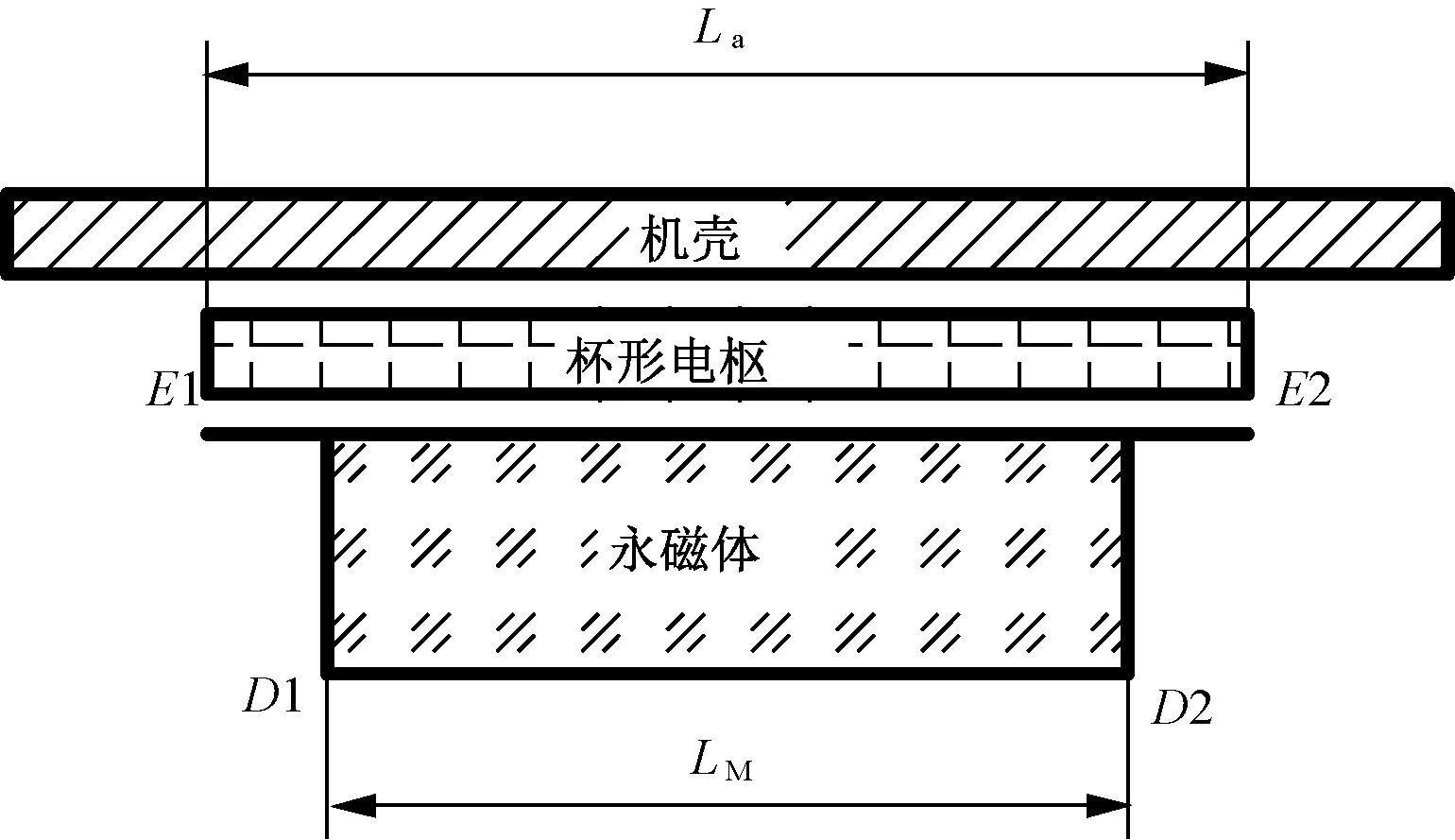
图6 磁矢位法计算端部漏磁模型

图7 磁矢位法仿真模型图

图8 D1点、D2点磁矢位

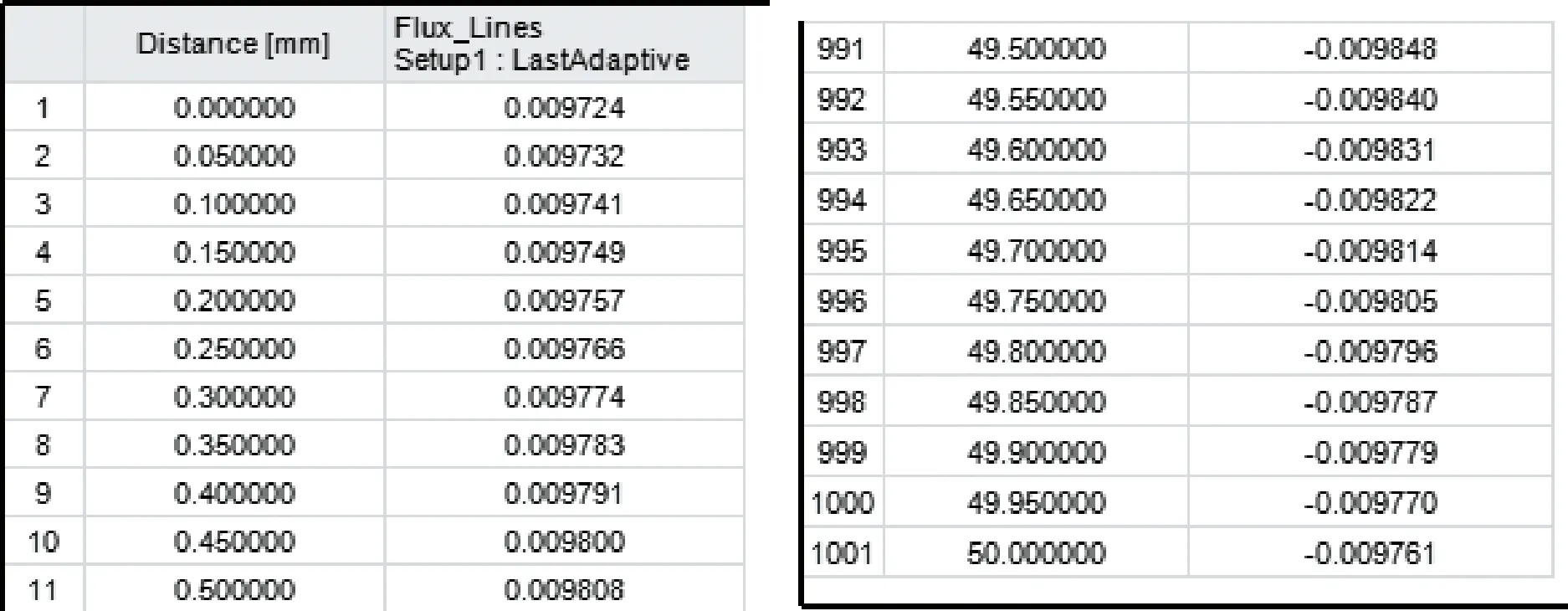
图9 E1点、E2点磁矢位

磁矢位法仿真得到D1、D2、E1、E2点磁矢位，计算得出电机1的漏磁系数：

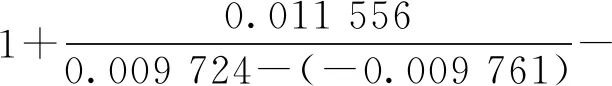
3 磁力线法计算漏磁系数

磁力线法计算漏磁系数是通过有限元仿真计算出电机的磁力线，通过数出总磁力线数量N和不与电枢绕组交链的漏磁力线数量n，计算出电机的漏磁系数[5]，其本质与磁矢位法相同。同样，该方法也需分别计算极间漏磁系数σ1和端部漏磁系数σ2。

(9)

(10)

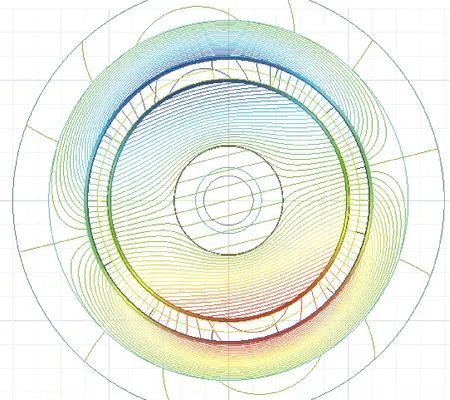
图10 极间磁力线图

极间漏磁和端部漏磁的磁力线图分别如图10和图11所示，总磁力线N为50条，极间漏磁力线n1为2条，端部漏磁力线n2为6条。漏磁系数：

(11)

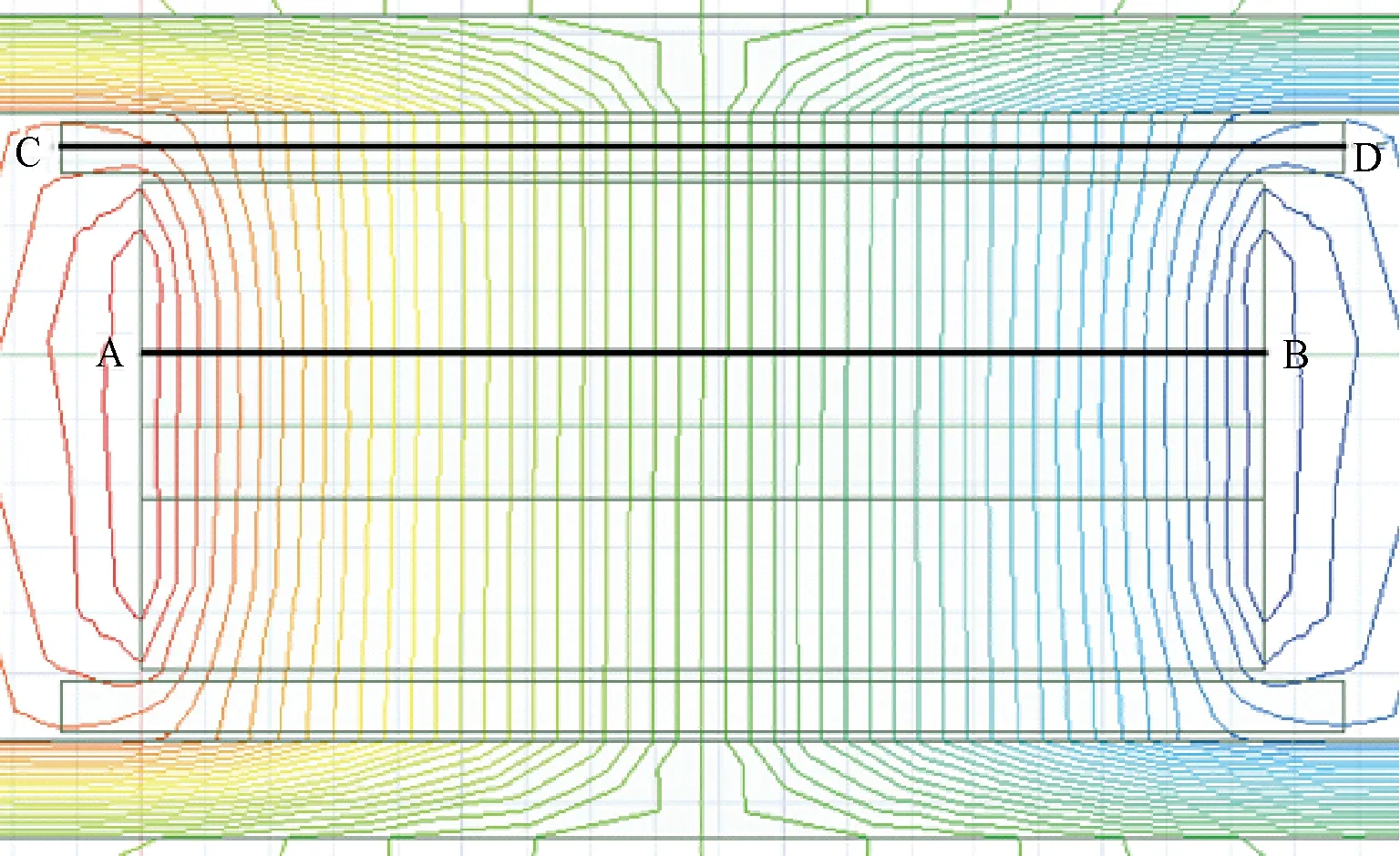
图11 端部磁力线图

磁矢位法和磁力线法得到的漏磁系数结果相同，相互印证两种计算方法的正确性。将漏磁系数的结果代入漏磁系数解析表达式，计算得出经验校正系数k=1.045。

为验证解析表达式的正确性，更换电机参数，以电机2(外径40 mm)的空心杯电机为例，极数2p=2；磁钢内径Din=11 mm；磁钢外径Dout=26.8 mm；磁钢轴向长度LM=38 mm；总气隙δ=3.4 mm；计算电枢长度Lef=45 mm。按照三种漏磁系数计算方法的结果如表1所示。从表1可以看出，更换电机参数后，解析法计算的漏磁系数与通过有限元分析的磁矢位法和磁力线法结果比较吻合，进一步验证了漏磁系数解析表达式的正确性。

表1 三种漏磁系数计算方法的计算结果对比

4 磁路饱和对漏磁系数的影响

以上计算均为在忽略空心杯电机的机壳磁阻情况下进行的。当机壳出现磁饱和时，电机的漏磁增大，漏磁系数也相应要增大，此时应修正漏磁系数解析表达式中的校正系数k。使用磁矢位法和磁力线法计算两型电机在饱和情况下的漏磁系数，如表2所示。将电机1的饱和漏磁系数代入解析表达式，得出k饱和=1.07k。使用该校正系数计算电机2在磁路饱和情况下的漏磁系数，结果与磁矢位法和磁力线法吻合。