换入换出不同向型换向装置换向流量误差分析

潘云飞，罗德章，刘桂雄

（1.广州能源检测研究院，广东 广州 510170；2.华南理工大学机械与汽车工程学院，广东 广州 510640）

0 引 言

应用于液体流量标准装置的换向装置主要有换入换出同向型与换入换出不同向型两种。换入换出同向是指换向器喷嘴在工作状态与非工作状态中相互切换时移动方向一致（如应用于日本国家计量院液体流量装置的换入换出同向型换向装置）[1]，换入换出不同向是指换向器喷嘴在工作状态与非工作状态中相互切换时移动方向相反（如应用于德国联邦物理技术研究院液体流量标准装置换入换出不同向型换向装置）[2]。目前国内外研究者主要集中研究换向装置换向运动重复性误差[3-5]，针对喷嘴摆动、分流器固定式换入换出不同向型换向装置换向过程中，喷嘴内部水流流场变化造成的换向流量误差所做研究较少，但该类换向流量误差客观存在,尤其在液体流量标准装置中不可忽视。为降低液体流量标准装置的不确定度，研究分析喷嘴摆动、分流器固定式换入换出不同向型换向装置换向过程换向流量误差具有实际意义。

1 换向流量误差原理分析

图1为应用换入换出不同向型换向器的液体流量标准装置结构示意图，图中虚线框部分为换向装置。换向装置工作原理为：1）喷嘴处于位置1，打开阀门，水流进入喷嘴，并从分流器左出口3流到回流罐，一段时间后喷嘴内水流稳定；2）启动气缸，流量表计时器启动计时，喷嘴从位置1摆动到位置2，水流由喷嘴经分流器出口4流到称重罐，换向装置完成换入过程；3）经过检定时间后，再次启动气缸，流量表计时器停止计时，喷嘴由位置2摆动到位置1，换向装置完成换出过程，至此，换向装置一个完整换向周期结束。

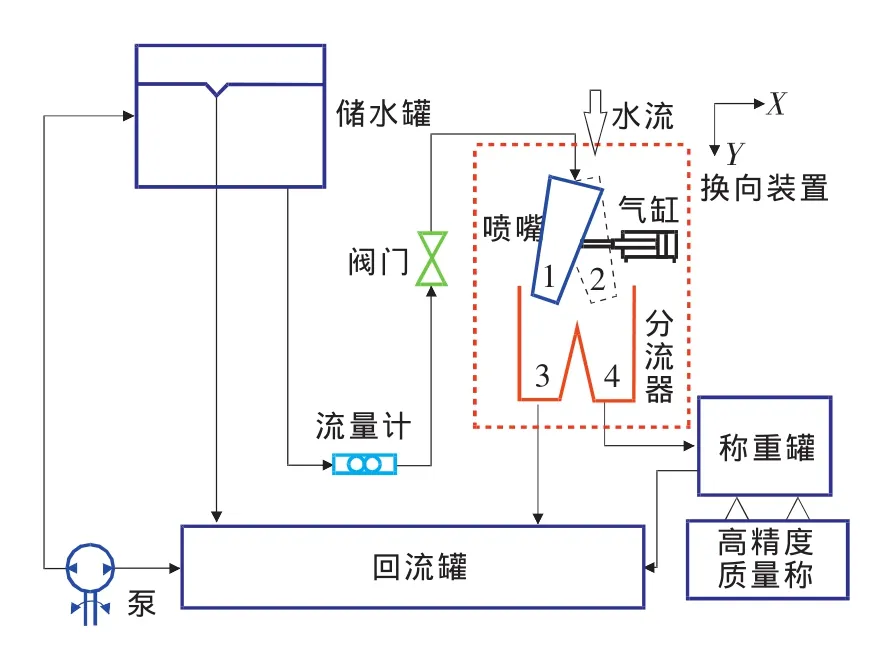
图1 液体流量标准装置结构示意图

图2为换向装置一个换向周期称重罐瞬时流量物理模型。tTIstart、tTIstop分别表示换向装置换入开始与换入结束时刻，tMstart、tMstop分别表示流量计计时器启动计时与停止计时时刻，tTOstart、tTOstop分别表示换向装置开始换出与结束换出时刻，qin表示任意时刻t称重罐瞬时流量，qconst表示换入过程结束时刻至换入过程开始时刻时间段内称重罐恒定瞬时流量。

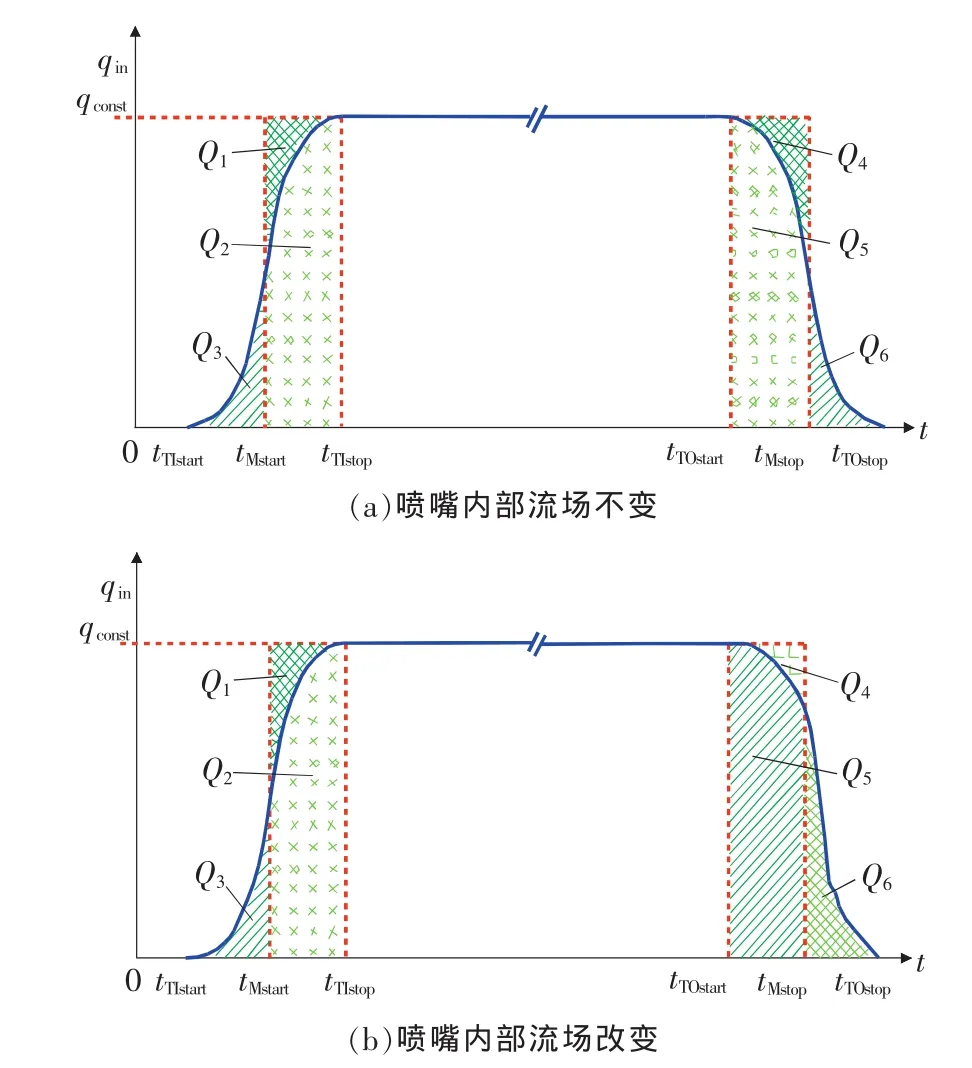
图2 换向装置一个换向周期流入称重罐的瞬时流量物理模型

由于存在计时启动延后误差Δt1=tMstart-tTIstart，Δt2=tMstop-tTOstart，流量表计时器启动计时时刻会延后于换向器启动时刻[6]，故流量计实际计时时间为Treal=tMstop-tMstart，换入时间为TTI=tTIstop-tTIstart，换出时间为TTO=tTOstop-tTOstart。

1）流量计实际流量QFreal为

2）称重罐实际流入流量QTreal为

3）换向流量绝对误差QE为

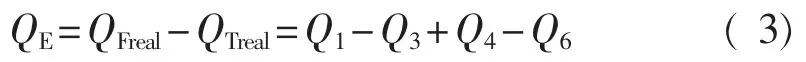
4）换入过程流入称重罐流量QTI为

5）换出过程流入称重罐流量QTO为

在喷嘴内部流场不变条件下，换向过程tTIstart～tTIstop段瞬时流量曲线与tTOstart～tTOstop段瞬时流量曲线相互对称，故只要设置流量表计时器计时启动延迟Δt1，使得Q1=Q3，在保证换向装置换向过程运动重复性一致、流量表计时器计时启动延迟一致、换入与换出时间相同条件下，则有 Δt1=Δt2，tTIstop-tTIstart=tTOstop-tTOstart，Q4=Q6，Q1+Q2=Q4+Q5，换向过程不存在换向流量误差。但由于喷嘴在摆动过程中内部流场会发生变化，故tTIstart～tTIstop段瞬时流量曲线与 tTOstart～tTOstop段瞬时流量曲线并不对称，在换向装置换入换出过程运动重复性一致、流量表计时器计时启动延迟一致、换入与换出时间相同条件下，可得Q1=Q3，Q1+Q2=Q4+Q5，但Q4≠Q6，称重罐实际流入流量QTreal=QTI+QTO+qconst（tTOstart-tTIstop），换向流量绝对误差QE=Q4-Q6=Q4+Q5-Q5-Q6=Q1+Q2-（ Q5+Q6）=QTI-QTO，故换向流量相对误差 E 为

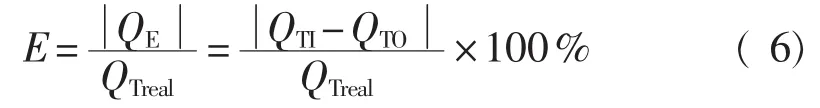
2 仿真方案

2.1 物理模型及网格划分

图3为仿真物理模型和网格划分示意图。如图所示，仿真实验将仿真对象分为1喷嘴、2过渡环境、3外部环境、4分流器左管道和5分流器右管道共5个部分，图 3（ a）组成部分 1～5 与图 3（ b）网格 1～5 相对应。

图中喷嘴入口处直径为1m，出口处直径为0.6m，喷嘴中线与竖直方向所成夹角为8°。考虑到换向装置物理模型关于X-Y平面互相对称，以X-Y纵截面为仿真对象划分网格，在满足实验要求条件下既可以高效率利用计算机资源，又可以节省仿真时间[7]。如图3（b）所示，采用块划分网格生成技术[8]对各组成部分进行四边形网格划分，然后将网格接合起来，形成仿真实验网格模型，网格质量＞0.9。

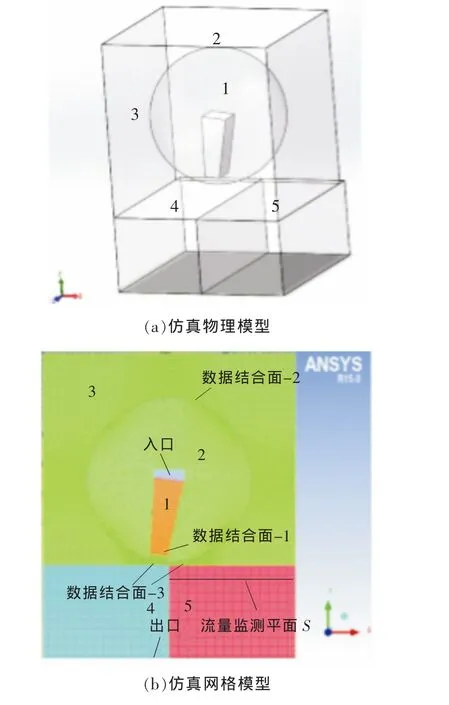
图3 仿真物理模型和网格划分

分流器右管道处设置有一水平瞬时流量监测平面S，喷嘴出口与过渡环境相接合处设置数据面-1，过渡环境与外部环境接合处设置数据接合面-2，外部环境、工作容器与旁路容器之间设置数据接合面-3，下方分流器出口处设置出口，其余各边界面均设置为wall。

2.2 仿真条件与过程

仿真计算时间步长设置为0.000 1 s。仿真模型初始化为空气单相状态，温度为25℃，喷嘴处于待换入状态，喷嘴入口处水流流速为5 m/s，水密度为998kg/m3。以竖直方向入水1s后，启动用户自定义（UDF）程序，喷嘴网格、过渡环境网格为滑移部分，以恒定角速度2rad/s逆时针绕原点旋转，实现换向装置换入过程，整个换入过程持续139.5ms。1s后，启动UDF程序，喷嘴网格和过渡环境网格以恒定角速度2rad/s顺时针绕原点旋转，实现换向装置换出过程，整个换出过程持续139.5 ms。记录换入换出过程监测面S瞬时水流量数据。

仿真采用流体体积函数（VOF）两相流模型[9]及显式体积分数模式[10]，可以最大程度地模拟实际水流流动情况。湍流模型采用RNG k-ε湍流模型[11]，该模型可达到比标准k-ε湍流模型更高的准确度。

3 仿真结果分析

t=1.0000，1.0465，1.9300，1.1395，2.0000，2.0465，2.9300，5.1395s时刻换向过程气-液相图以及喷嘴内部水流流场分布图如图4所示。可以看出，喷嘴摆动过程中内部流场处于持续变化状态。

在换向周期内，喷嘴内部水流速度场呈不对称分布，这就导致换入换出过程中喷嘴出口流速分布不对称并引起换向流量误差。

图5为换向仿真过程称重罐瞬时流量曲线图。 取 tTOstart-tTIstop=50 s，由式（ 3）～式（ 6）可得：QTI=378.596 4 kg，QTO=384.872 7 kg，QE=-6.276 3 kg，QTreal=250263.4691kg，E≈0.0025%。其物理意义是：换入换出过程称重罐瞬时流量曲线不对称，换入换出流量相对误差达0.0025%。

4 结束语

本文主要仿真分析并估计换入换出不同向型换向装置换向流量误差。结果表明即使流量计启动计时时刻设置合理，并保证装置换入换出过程运动重复性一致、计时器计时启动延迟一致、换入换出时间相同，换向过程仍会产生换向流量相对误差，达0.0025%。后续研究发现减小该类换向流量误差是降低液体流量标准装置不确定度的关键手段。

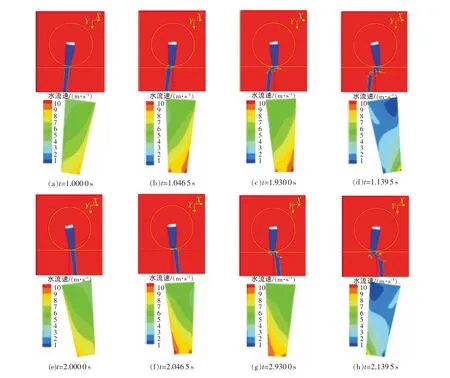
图4 换向过程气-液相图以及喷嘴内部水流流场分布图

图5 换向仿真过程称重罐瞬时流量曲线图

[1]Shimada T， Oda S， Terao Y， et al.Development of a new diverter system for liquid flow calibration facilities[J].Flow Measurement and Instrumentation，2003，14（ 3）：89-96.

[2]Rainer E，Hans-Joachim B.Improvement of liquid flow calibration by applying special measurement and control strategies[J].Flow Measurementand Instrumentation，2003，14（ 6）：225-282.

[3]Doihara R， Shimada T， Oda S， et al.Development of weighing tank system employing rotating double wing diverter[J].Flow Measurement and Instrumentation，2006，17（ 3）： 141-152.

[4]马龙博，郑建英，赵健亮.基于换入换出同向方法的开式换向器设计及不确定度评定方法研究[J].制造业自动化，2013，35（ 22）：119-122.

[5]陈晓敏，马龙博，李东升.换入-换出同向型换向器的研究[J].自动化仪表，2013，34（ 3）：62-66.

[6]Rainer E，Hans-Joachim B.Model-Based flow diverter analysis for an improved uncertainty determination in liquid flow calibration facilities[J].Measurement Science and Technology，2010，21（ 2）：1-11.

[7]潘传九，葛文娜，陆晓峰.基于CFD的搅拌流场模拟及预测研究[J].中国测试，2012，38（ 6）：13-16.

[8]许孟辉，邱志平.三角形机翼参数化有限元网格划分与调整方法[J].北京航空航天大学学报，2015，60（ 3）：1-7.

[9]Ménarda T， Tanguyb S， Berlemonta A.Coupling level set/VOF/ghost fluid methods:validation and application to 3D simulation of the primary break-up of a liquid jet[J].International Journal of Multiphase Flow，2007，33（ 5）：510-524.

[10]Nektarios K， John G B， Nicolas C M.Evaluation of reynolds stress， k-ε and RNG k-ε turbulence models in street canyon flows using variousexperimental datasets[J].Environmental Fluid Mechanics，2012，12（ 4）：379-403.

[11]于国飞.多用途汽车正面碰撞特性的数值模拟[J].中国测试，2013，39（ 6）：118-121.