底盘测量仪研制及标定分析

胡鹏浩，朱 良，赵 鹏

（合肥工业大学，安徽 合肥 230009）

0 引 言

汽车底盘上有很多基准点，这些基准点既是底盘冲压、焊接制造时的基准，也是底盘碰撞后修复的工艺基准和测量基准。通过检测底盘上基准点之间的相对位置及尺寸便可以判别产品是否合格，底盘的修复也需要进行这样的检测。大型直角三坐标测量机能胜任该测试任务，但价格昂贵，环境要求苛刻，不适宜在车间和汽车4S店内使用。柔性关节坐标测量机便于移动、测量准确度也满足要求，但测量空间相对较小。光笔测量机准确度和测量范围均能满足要求，但目前只有进口产品，价格较高。

鉴于此，研发一款面向汽车底盘测量的专用高准确度低成本仪器对于底盘检测以及碰撞修复后的质量评估具有重要意义，同时也有较好的市场前景[1]。本文在充分考虑汽车底盘结构及特点的基础上，结合双平行关节测量机[2]和柔性关节坐标测量机的优点，研制了测量设备，并开展后续相应测量误差建模、仪器标定方法等研究工作。

1 样机及测量模型

汽车底盘的尺寸较大，一般在4500mm×2000mm范围内，但在高度及垂直方向上尺寸较小，一般在300mm以内，同时对测量准确度的要求也相对较低。针对这些特点，基于关节臂测量机的相关技术，进行了结构设计和样机研制。

如图1所示，仪器主要由底座、5个关节、3段连接杆件和测头4部分组成。根据底盘在水平面内X-Y方向尺寸大，而Z方向尺寸较小的特点，仪器采用双平行关节扩大在X-Y方向的量程，关节4绕Y轴回转满足Z方向所需量程，关节3、4、5的轴线分别垂直正交，测头可绕X轴回转，测头在实际测量中有 3 个工位，它们分别与 X 轴成 0°、45°、90°，以方便测量底盘上的孔及槽。每个关节上用一对P4级NSK精密角接触球轴承、一个圆光栅传感器、一个滑环实现信号输出和关节无限回转。各关节配独立的测量电路和信号采集，用蓝牙传输至计算机。根据用户对精度要求的不同，可选配不同准确度等级的圆光栅，甚至在一台仪器上，5个关节所用圆光栅的准确度等级也可以不同，离底座越远的关节，其圆光栅准确度越低。在实际测量中，其操作方式与关节臂测量机相似，由操作者拖动测头至被测点，手动触发同步采集5个圆光栅读数值，换算出空间坐标[3]。

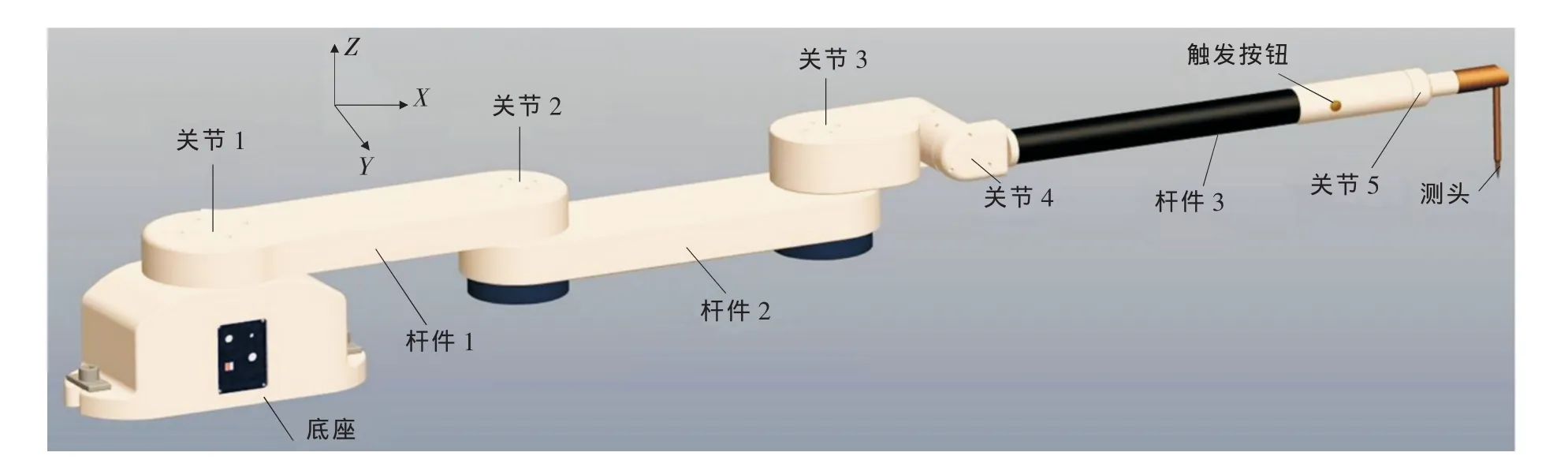
图1 底盘测量仪结构

测量仪为空间串联式开链连杆结构，与传统串联式机器人类似，依照机器人学中常用的D-H建模方法[4]，在每个关节处分别建立参考坐标系。如图2所示，其中坐标系O0X0Y0Z0为基座坐标系，O1X1Y1Z1到O5X5Y5Z5分别为在5个关节处所建立的参考坐标系。由于测量仪末关节与测头点不重合，需要一个齐次矩阵将其联系起来，在与末关节相连的测量臂末端处建立参考坐标系O6X6Y6Z6，在测头处建立参考坐标系 O7X7Y7Z7。

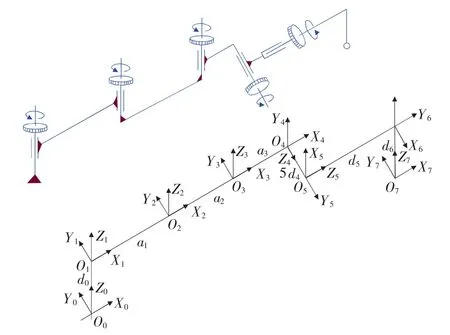
图2 测量仪运动学模型

仪器前3个关节平行，如直接采用D-H建模，得到的齐次矩阵将是病态的[4-5]，Robert P.JUDD[6]提出了平行关节轴的4参数修正模型，能很好地解决这个问题，但在运用到后面两个相邻垂直关节时，齐次矩阵又会变为奇异阵。Veitschegger[7]在此基础之上提出了5参数MDH模型，本质上是增加一绕y轴的旋转变换：Rot（yi，βi），该模型既克服了D-H模型在两平行关节处齐次矩阵病态的问题，又解决了4参数修正模型在相互垂直的两相邻关节处齐次矩阵奇异的问题。

在此采用5参数MDH模型，相邻关节变换的齐次矩阵如下：

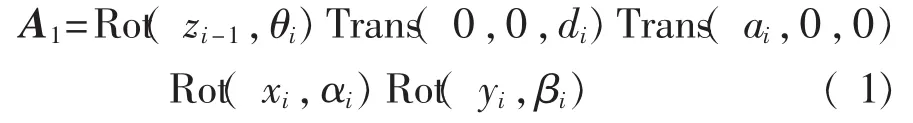
式中：θi——xi-1轴与xi轴之间的夹角；

di——相邻两杆（连杆i-1和连杆i）所连接的3条轴心线所确定的两条公法线之间的距离；

ai——zi轴和zi-1轴轴心线的公法线长度；

αi——zi轴和zi-1轴轴心线的夹角；

βi——关节轴线从yi-1轴到yi轴所转过的角度。

此处将测量仪模型中的非关节变换A0和A6也统一写成齐次矩阵A的形式，则测量仪由基坐标系到测头坐标系的齐次变换T矩阵可表示为

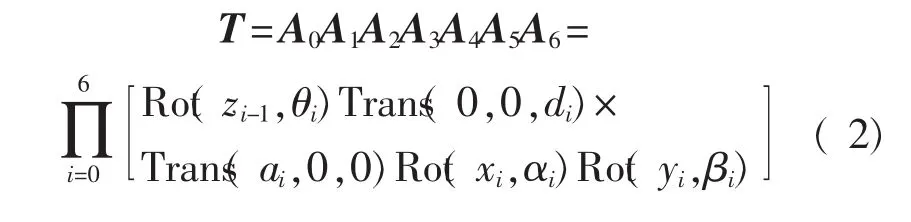
由此，可以得出测头坐标表达式：

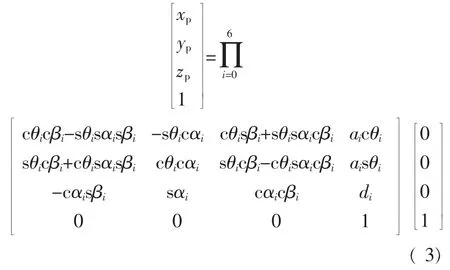
式中 s、c为 sin、cos符号的简写。

2 误差分析及建模

影响底盘测量仪精度的误差源很多，从仪器结构特点及测量模型来看，测量仪的误差来源主要有以下方面[8]：角度传感器引起的误差、结构参数误差、力变形误差、热变形误差、部件运动误差、数据采集系统误差、轴系回转误差等。在这些主要误差源中，除了数据采集系统误差，其他项误差都会以一定的形式表现或使仪器的实际结构参数发生变化，这就需要通过标定来进行修正。与关节臂测量机、并联机构、机器人相似，标定也是提高底盘测量仪精度的一项重要措施，在底盘测量仪标定中有两个关键步骤：首先是用底盘测量仪测量特定的标准件来获取误差参数信息；其次是完成参数识别，即将所获误差参数代入测量误差模型构成非线性误差方程组，并通过特定的优化算法收敛求解出结构参数，再将其替换到测量模型中[9]。

2.1 标定建模

在测量模型式（3）中包含23项结构参数误差，分别是5个关节的零位误差Δθi0，测头工位误差Δθ6，关节扭角误差 Δαi，连杆长度误差 Δai，基座高度误差 Δd0，连杆距离误差 Δd3、Δd4、Δd5，测头长度误差Δd6，以及平行关节结构所引入的误差 Δβ1、Δβ2。运用偏微分法可得到测量误差模型为

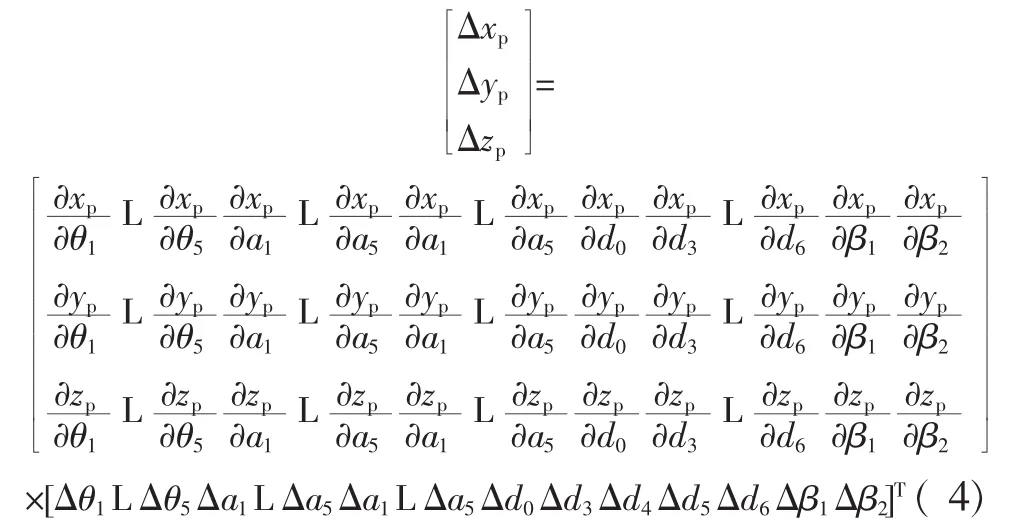
基于空间两点距离公式可以写出测量仪的距离标定模型：

式中：d——测得的空间两点间距；

Θ1，Θ2——指测量仪在测量空间第1点和第2点时的关节转角输出向量；

b——23个待辨识参数所组成的向量。

2.2 误差测量及参数辨识

在标定中，仪器通过测量专门研制的三维球列来获取测量误差信息，获取足够多组的（ Θ1，Θ2，b）测量样本后，将测量值与标准值相减，其差值F可表示为

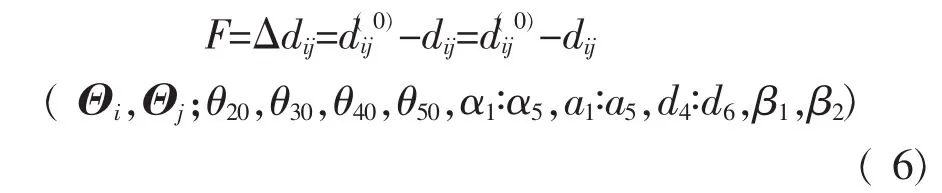
将测得的误差值代入式（4），得到一个非线性误差方程组，求解方程即可获得待辨识参数的估计值。此处采用常用的高斯-牛顿法（G-N法）求解。

对距离标定模型中的各项待辨识参数求偏导可以求得其Jacobin矩阵：

在应用高斯-牛顿法进行参数辨识时，通常会要求Jacobin矩阵列线性无关。这里考虑该矩阵中各列的线性相关性，可以得到：

此处4个偏导均为零说明相应的4个结构参数（ θ10、θ6、d0、d3）对距离标定结果没有影响，应将 Jacobin矩阵中的对应列予以剔除。剔除后，将19项线性无关的参数重新编号，并依然记它们为 b1，b2，…，b19，则相应的Jacobin矩阵即改写为如下形式：

同时参数向量b也变成19维的列向量，将b中各参数的理论值作为初始值进行G-N迭代至满足收敛条件时得到的向量b*中的各元素的数值即为相应待辨识参数的估计值，亦即标定结果。

3 标定实验

3.1 三维球列设计

柔性关节坐标测量机的标定方法较多，如单点锥窝法、大尺寸量块法、直角三坐标法、激光跟踪仪法等[10-12]。考虑到底盘测量仪的结构特点，期望选择一种标定实物，其结构能保证在进行标定测量实验时，仪器的标定测量状态能和它将来的实际工作状态相似，这样便于保证仪器的工作精度。为此，选择了三维球列，三维球列法在直角坐标测量机标定及并联机构标定中应用比较多，在欧洲和日本应用广泛[13-14]。

在确定三维球列尺寸时采用以下策略：汽车底盘总体具有一定的对称性，将其均分为4个象限，选取2个象限，将该部分从整个底盘上切割下来以方便测量。在其内X，Y方向上分别按照间距100mm取点，用底盘测试仪获得各点相对高度数据，结合实验条件对这些样本数据进行分析、综合、取整，最终选取了12个数据点作为三维球列的Z坐标，如表1所示。

表1 标定杆高度

所制三维球列如图3所示，各标定杆的间距为200mm，各杆顶端留有锥窝嵌入钢球，钢球选自轴承的滚珠，圆度误差及尺寸误差均在1 μm以下，这样的结构及尺寸基本模拟了底盘轮廓的尺寸特征，球列上各球之间的中心距用三坐标测量机预先测得，并视为标准尺寸用于标定。

3.2 标定测量

图3 使用三维球列进行标定实验

如图3所示，在实际标定中，拉开三维球列与测量仪的距离，并分别将三维球列放置在仪器的前后左右，尽量模仿仪器测量底盘时的工作状态。测量仪在每个钢球上各采5个点，用于计算球心坐标，并同步记录各个关节编码器的角度值。完成数据采集后，通过球心间距与球列间距标准值组成的目标函数进行G-N迭代，直到获得满足精度要求的参数修正值。数据处理程序用Matlab软件编写，修正值如表2、表3所示。

将表2、表3中参数的修正值代入测量模型后，获得新的测量模型，使用修正模型重新测量三维球列球间距，部分新测量误差如表4所示。

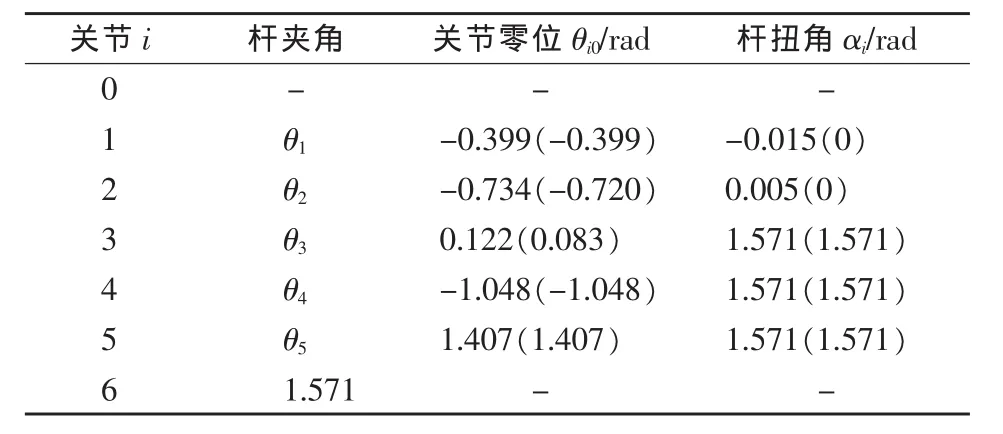
表2 结构参数初始及标定值1）

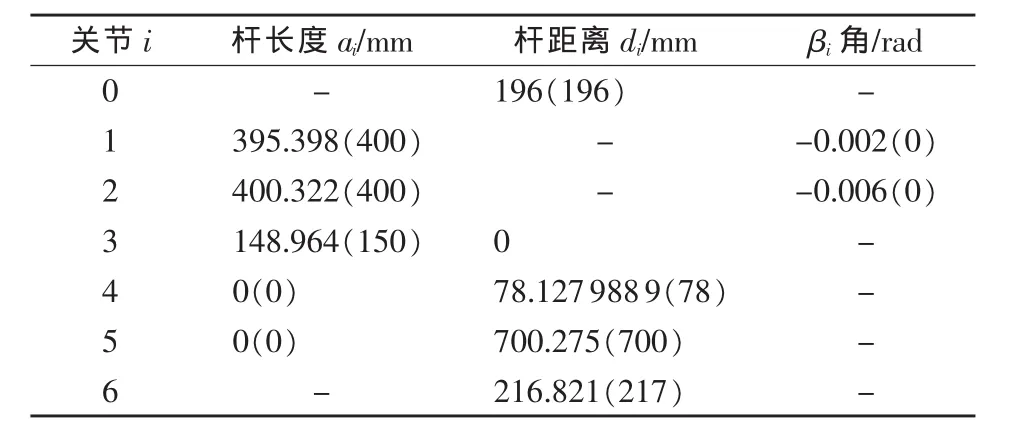
表3 结构参数初始及标定值

表4 标定后的仪器测量误差

通过数据分析可知，标定前，测量仪的测距准确度一般在mm级，标定后该测量仪的测距误差均在±0.5mm以内，总体上测量值偏小，说明样机内还有系统误差没有消除，但测量准确度同标定之前相比有明显提高。

4 结束语

1）运用5参数MDH法建立了汽车底盘测量仪的测量模型、测量误差模型，给出了基于三维球列法的参数标定模型。

2）依据汽车底盘的结构特点，设计和研制了三维球列标定实物，以贴近仪器工作状态的方式进行标定测量。

3）运用高斯-牛顿法实现仪器结构参数的辨识，标定后仪器准确度在4 m范围内可达0.5 mm，仪器准确度明显提高。

[1]程本付.车身电子测量系统在碰撞修复中的重要作用[J].汽车维修与保养，2008（ 8）：62-64.

[2]Lotze W.Scanmax-a novel 3D coordinate measuring machine for the shopfloor environemt[J].Measurement，1996，18（ 1）：17-25.

[3]胡鹏浩，胡毅，于连栋，等.一种关节式电子车身测量机：中国，ZL 2012 2 0466868.7[P].2012-09-13.

[4]殷际英，何广平.关节型机器人[M].北京：化学工业出版社，2003：20-30.

[5]杨睿嫦，尚平，王鑫.平行双关节坐标测量机的测量模型及误差分析[J].工具技术，2010，44（ 8）：86-90.

[6]Judd R P， Knasinski A B.A technique to calibrate industrial robots with experimental verification[J].Robotics and Automation IEEE Transactions，1990，6（ 1）：20-30.

[7]Veitschegger W，Wu C H.A method for calibrating and compensating robot kinematic errors[C]∥Robotics and Automation Proceedings1987 IEEE International Conference on IEEE，1987（ 4）：39-44.

[8]林铿.关节臂式坐标测量机的误差分析与补偿研究[D].杭州：浙江大学，2010.

[9]高贯斌.关节臂式坐标测量机自标定方法与误差补偿研究[D].杭州：浙江大学，2010.

[10]汪平平.柔性坐标测量机准确度理论及应用技术研究[D].合肥：合肥工业大学，2006.

[11]程文涛.关节式柔性坐标测量机关键技术研究[D].合肥:合肥工业大学，2008.

[12]Wang X Y，Liu S G，Zhang G X，et al.Calibration technology of the articulated arm flexible CMM[J].Key Engineering Materials，2008（ 381-382）：161-164.

[13]张国雄.三坐标测量机的发展趋势[J].中国机械工程，2000，11（ 1-2）：222-226.

[14]Furutani R， Shimojima K， Takamasu K.Parameter calibration for non-cartesian CMM[J].VDI Berichte，2004（ 1860）：317-326.