血吸虫病在多个染病者群体传播的S-DI模型的稳定性分析

甘莉娟，薛 梦，Sakhone Sysavathdy，齐龙兴

（安徽大学数学科学学院，安徽合肥230601）

血吸虫病在多个染病者群体传播的S-DI模型的稳定性分析

甘莉娟，薛 梦，Sakhone Sysavathdy，齐龙兴

（安徽大学数学科学学院，安徽合肥230601）

主要介绍血吸虫病在多个染病者群体传播的S-DI模型,对于两种不同的发生率产生不同的模型,分别求出其平衡点及疾病爆发的阈值,并且分别判断出无病平衡点和地方病平衡点的局部稳定性,并进行了数值模拟。

血吸虫病；S-DI模型；双线性发生率；标准发生率；稳定性

血吸虫病是一种严重危害人类健康的寄生虫病,据世界卫生组织于1995年估计,全球有75个国家和地区有血吸虫病的流行,受威胁人口约6.25亿,感染血吸虫病者1.93亿。我国也是全球血吸虫病危害最严重的国家之一。

目前,在实际防病,治病及科研等方面还存在着一系列的问题。当然,在研究血吸虫病传播的模型中,许多人已经做了很多的努力[1-6]。我们已经考虑了很多因素对血吸虫病传播的影响，例如宿主的潜伏期及血吸虫配对结构等等[1]。

影响血吸虫病流行的因素中水源是非常重要的因素之一,血吸虫生活史中的许多阶段都是在有水的条件下完成的,人们接触含有血吸虫的水源的程度不同，其受感染的程度也不同。本文就这一因素用数学的方法来探讨,希望为今后血吸虫病的控制和预防有很好的引导作用。

本文主要介绍了血吸虫病在多个染病者群体传播的S-DI模型,引入判断该模型稳定性的方法[2]。主要针对两种不同的发生率来介绍S-DI模型,并由此判断血吸虫病未来局部传播趋势。

1 模型的建立

由血吸虫病的传播机理可知，由于易感者接触含有血吸虫的水源的程度不同，使其受感染的程度也不同,因此我们可将其分为轻度感染者和重度感染者两类,分别用I1和I2表示,每一子群体中的病人均可与易感者S接触但有不同的有效接触率和移出率。假定输入率为常数K=μS0,且均为易感者,有效接触率系数为β,自然死亡率系数为μ,移出率系数为γ。

若采用双线性发生率,则相应的S-DI模型为[3]

若采用标准发生率,则相应的S-DI模型为

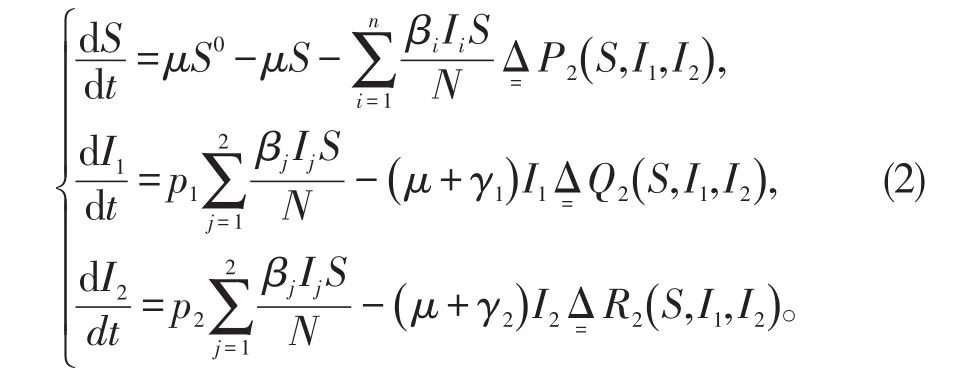
其中pi为染病者进入Ii群体的比例系数,;γi是Ii类病人的移出率系数;βi是Ii类病人的有效接触率系数。

2 平衡点的稳定性

对于上述两种模型的稳定性,主要思路：(1)有正平衡点的情况下求出正平衡点;(2)对该方程系统进行线性化,得到相应的线性系统;(3)应用常微分方程理论求出相应的特征方程和特征根,判断根的实部是否是负的;有负实部,则该系统的平衡点局部渐近稳定,否则不稳定。

2.1 双线性发生率模型

为求系统(1)的平衡点,令其右端为0,从而求得可能存在的两组解分别为,

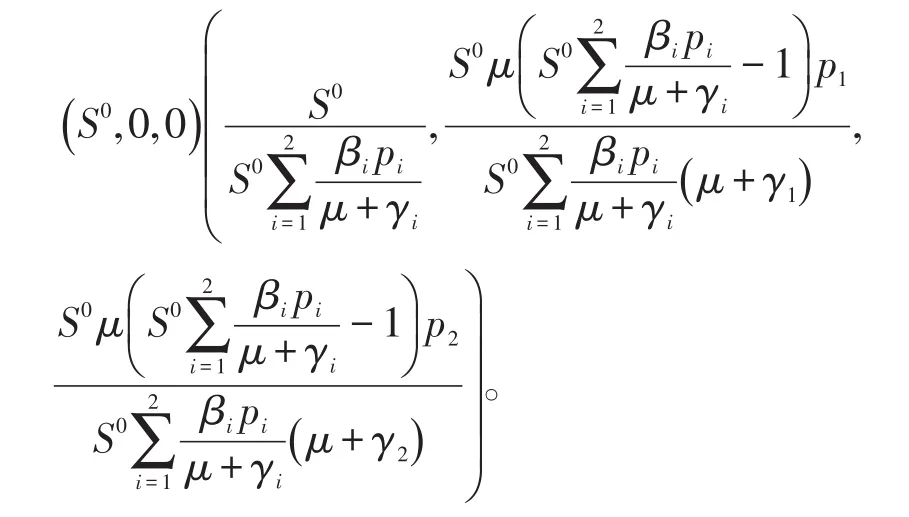
下面分两种情形讨论平衡点的存在性及稳定性。令

在上式中pi是染病后成为Ii类型病人的概率,是Ii类病人的平均患病期。从而,便是当人群全是易感者（流行初期）S0时，一个病人在其平均患病期内所传染的人数,所以上式所定义的阈值R0便是基本再生数。

当R0＜1时,系统(1)仅有唯一平衡点E0(S0,0,0),从而由其特征根的符号判断E0(S0,0,0)的稳定性[4]。系统(1)在E0(S0,0,0)点的Jacobian矩阵是

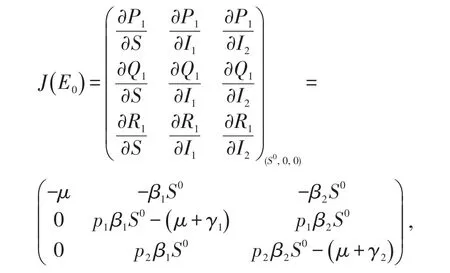
其特征方程为

其特征根

当R0＞1时,系统(1)除了无病平衡点E0(S0,0,0)外,还有一地方病平衡点E1=(S+,I1+,I2+),其中

此时,由于R0＞1,容易验证无病平衡点E0(S0,0,0)不稳定,下面证明当R0＞1时,地方病平衡点E1局部渐近稳定。

系统(1)在地方病平衡点E1的特征方程为

当R0＞1时,容易验证

因此由Hurwitz判别定理[5]知,特征方程的根全都具有负实部,即当R0＞1时,地方病平衡点E1局部渐近稳定。

2.2 标准发生率模型

为求系统(2)的平衡点,令其右端为0,从而求得可能存在的两组解分别为,

下面分两种情形讨论平衡点的存在性及稳定性。令

上式R0与易感者S0无关。由系统(2)可以看出是Ii类病人的平均患病期,故R0便是一个病人平均患病期内有效接触的个体数,即有效接触数。

当R0＜1时,系统(2)仅有唯一平衡点E0(S0,0,0),从而由其特征根的符号判断E0(S0,0,0)的稳定性[4]。系统(2)在E0(S0,0,0)点的特征根分别为

故点E0(S0,0,0)是局部渐近稳定的。此时E0为无病平衡点。

当R0＞1时,系统(2)除了无病平衡点E0(S0,0,0)外,还有一地方病平衡点E2=(S∗,I1∗,I2∗),其中

此时,由于R0＞1,容易验证E0(S0,0,0)不稳定,下面证明当R0＞1时,地方病平衡点E2局部渐近稳定。

系统(2)在地方病平衡点E2的特征方程为

容易验证d2＞0,d2d1-d0＞0。因此,由Hurwitz判别定理[5]知,特征方程的根全都具有负实部,即当R0＞1时,地方病平衡点E2(S∗,I1∗,I2∗)局部渐近稳定。

3 数值模拟

3.1 双线性发生率

选取S0=1,μ=0.01,β1=0.05,β2=0.1,p1=0.4,p2=0.6,γ1=0.3,γ2=0.2 作为系统(1)的一组参数值,计算可得R0=0.2074。由于R0＜1时,系统(1)的无病平衡点是局部渐近稳定的(如图1)。

又选取S0=1,μ=0.01,β1=0.05,β2=0.1,p1=0.4,p2=0.6,γ1=0.03,γ2=0.02 作为系统(1)的另一组参数值。计算可得R0=1.5000。由于R0＞1时,系统(1)的地方病平衡点也是局部渐近稳定的(如图2)。

图1 系统（1）的无病平衡点是局部渐近稳定

图2 系统（1）的地方病平衡点也是局部渐近稳定

3.2 标准发生率

选取同3.1相同的参数值,分别算得R0=0.2074和R0=1.5000。当R0＜1时,系统(2)的无病平衡点是局部渐近稳定的(如图3)。当R0＞1时,系统(2)的地方病平衡点也是局部渐近稳定的(如图4）。

图3 系统（2）的无病平衡点是局部渐近稳定

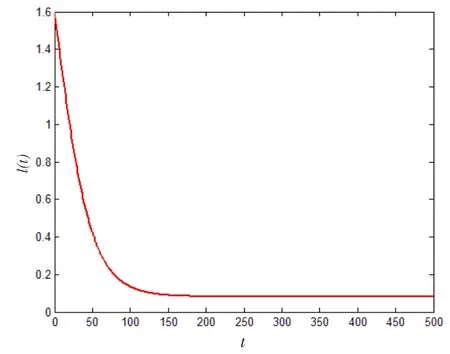
图4 系统（2）的地方病平衡点也是局部渐近稳定

4 讨论

讨论了血吸虫病在多个染病者群体传播的SDI模型,应用Hurwitz判别定理对两种不同发生率的模型稳定性的分析,证明了无病平衡点和地方病平衡点的局部稳定性。

对于双线性发生率模型,我们发现其基本发生率与S0有关,说明疾病流行与否与最初人口基数有关,那么在控制疾病时,我们可尝试采取分散人口或隔离等方式,这样将有助于控制疾病的传播。

我们还发现当R0＜1时,两个模型都仅有无病平衡点,它是局部渐近稳定的,说明血吸虫病将不会流行;当R0＞1,两个模型除无病平衡点外还有一地方病平衡点。此时无病平衡点不稳定,而地方病平衡点局部渐近稳定,说明血吸虫病流行而导致地方病产生。

从这两个模型我们可以看出,虽然发生率不同,但是数学结论类似。这也说明改变发生率对这类模型的主要结论影响不大,由于考虑到双线性发生率形式简单便于研究,在今后的研究中我们将以双线性发生率来考虑,为今后有关血吸虫病的研究做更多的努力。

[1]L X Qi,J A Cui,Y Gao,et al.Modeling the schistosomiasis on the islets in Nanjing[J].Int J Biomath，2012(5)：12500371-12500377.

[2]J Hyman,J Li.An intuitive formulation for the reproductive number for the spread of diseases in heterogencous populations[J].Math Biosci,2000(167)：65-86.

[3]马知恩.传染病动力学的数学建模与研究[M].北京：科学出版社,2004.

[4]马知恩,周义仓.常微分方程的定性与稳定性方法[M].北京：科学出版社,2001.

[5]王高雄.常微分方程[M].北京：高等教育出版社,2006.

[6]王爱丽.具有多种传播方式的介水传染病模型的稳定性[J].安徽大学学报，2015，39（2）：17-23.

The Stability Analysis of S-DI Model of Schistosomiasis Spread in the Multiple Infected Population

GAN Li-juan,XUE Meng,Sakhone Sysavathdy,QI Long-xing
(School of Mathematical Sciences,Anhui University,Hefei Anhui,230601)

This article mainly introduces the S-DI model of schistosomiasis spread in the multiple infected population.For two kinds of different incidence of different models,we find out the equilibria and threshold of disease outbreaks.The local stability of the disease-free equilibrium and the endemic equilibrium are determined in theory and by numerical simulations respectively.

schistosomiasis;S-DI model;bilinear incidence;standard incidence;stability

O151.26

A

1674-0874(2015)04-0005-04

2015-05-12

国家自然科学基金项目[11401002]；安徽省自然科学基金项目[1208085QA15]

甘莉娟（1992-），女，安徽合肥人，在读硕士，研究方向：应用数学。

〔责任编辑 高海〕