时间模上多-点边值问题两个正解的存在性
2015-11-08乔世东
乔世东
(山西大同大学数学与计算机科学学院,山西大同 037009)
时间模上多-点边值问题两个正解的存在性
乔世东
(山西大同大学数学与计算机科学学院,山西大同 037009)
运用锥上的不动点定理Avery和Henderson,讨论时间模T上的二阶非线性动力学方程多-点边值问题至少有两个正解的存在性。
正解;时间模;边值问题;不动点定理;锥
在2004年,何志民[1]研究了m-点边值问题

至少有两个正解,其中T是一个时间模,ξi∈(0,T)T,
在2014年,我们的前期工作[2]运用Krasnoelskii锥上的不动点定理,讨论时间模上的二阶非线性动力学方程多-点边值问题。

至少有一个正解的存在性。
运用锥上的Avery-Henderson不动点定理,讨论时间模上的二阶非线性动力学方程多-点边值问题(2)至少有两个正解的存在性。其中T是一个时间模,a<ξ<η<b。另外,我们还假设以下的条件成立:
(A1)α,β,γ,δ≥ 0,μ1,μ2> 0 ;
(A2)f:[0,∞]→[0,∞)是连续的且f(u)>0;
(A3)q∈Crd([a,b],[0,∞))且存在t0∈[a,b],使得q(t0)>0。
记



引理1设条件Λ≠0,∇≠0,则u(t)是方程(2)的唯一解,当且仅当

引理2 设条件Λ≠0,∇≠0,则

因此,引理2成立。
下面假设
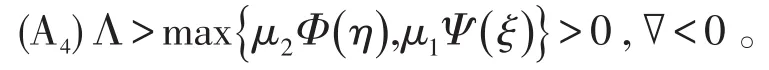
引理3 设条件(A1)、(A2)成立,则方程(2)的解u(t)满足u(t)≥0,t∈[a,b]⊂T。
令E=Crd[a,b]是一个巴拿赫空间,其上泛数定义 为,定义一个锥P⊂E,且

引理4设u∈P,则

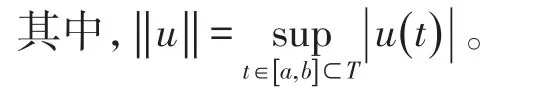
证明 由引理1和引理2,有

由引理2和(7)

证毕。
边值问题(2)有解u=u(t)当且仅当u是下列算子方程的解。

定理1[3]设P是实巴拿赫空间E的一个锥,集合

如果ν,Φ是定义在P上的增加的,非负的连续函数,让θ是一个定义在P上非负的连续函数且有θ(0)=0满足对一些正的常数r,M及所有的Φ(u)≤θ(u)≤ν(u),‖u‖≤MΦ(u)。又假设存在常数0<p<q<r满足下列条件,θ(λu)≤λθ(u),0≤λ≤1,u∈∂P(θ,q) 。假设是P上的一个全连续算子满足下列条件:
(1)Φ(Au)>r对所有的u∈∂P(Φ,r);
(2)θ(Au)<q对所有的u∈∂P(θ,q);
(3)P(ν,p) ≠φ,和ν(Au)>p对所有的u∈∂P(ν,p),则A至少有两个不动点u1,u2,满足p<ν(u1),θ(u1)<q和q<θ(u2),Φ(u2)<r。
定义非负连续增函数Φ,θ,ν满足

对每一个u∈P,有Φ(u)=θ(u)≤ν(u)。另外,对每一个u∈P,由引理3知Φ(u)=u(η)≥Λ1‖u‖。
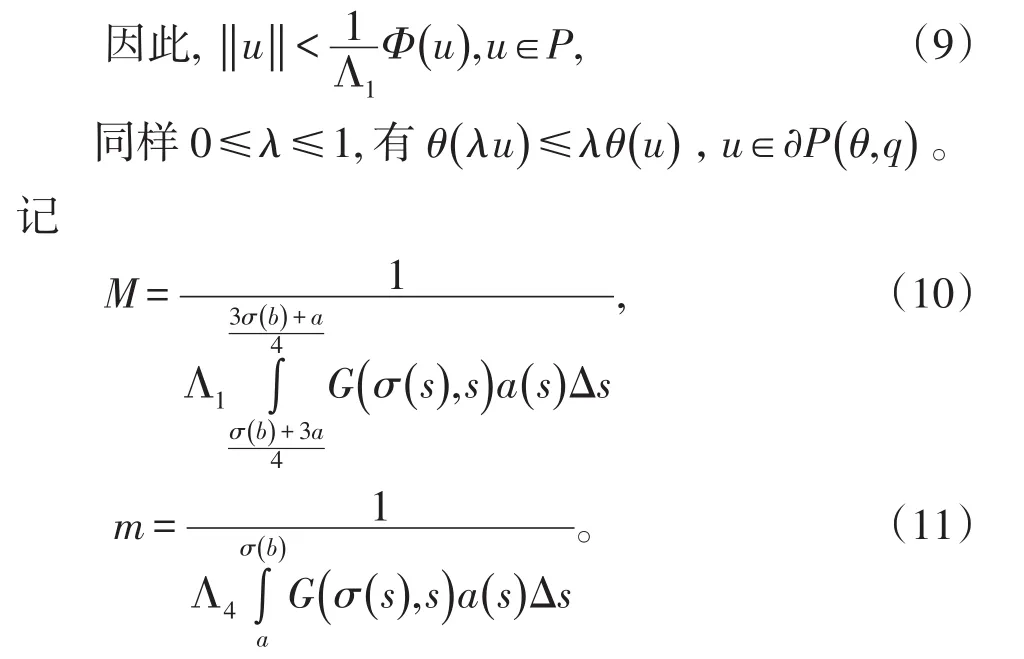
定理2设条件(A1)~(A4)成立,又设存在常数0<p<q<∞ 满足:

则边值问题(2)至少有两个正解u1,u2,满足ν(u1) >p,θ(u1) <q,和q<θ(u2),Φ(u2)<r。
证明验证定理1的所有条件都满足。
定义一个全连续积分算子A:P→P满足:

对于u∈P,t∈[a,b]⊂T.,易知 (Au)(t)满足方程(3)。

从而定理1的条件(1)满足。
设u∈∂P(θ,q),则

又因为u∈P,有,t∈[a,b]⊂T。
由假设条件(c2)知,得到

从而定理1的条件(2)满足。

由假设条件(c3)得到

从而定理1的条件(3)满足。
由于定理1的所有条件都被满足,则边值问题(3)至少有两个正解u1,u2,满足ν(u1) >p,θ(u1)<q,和q<θ(u2),Φ(u2)<r。
[1]Zhimin He.Existence of two Solutions of m-point Boundary Value Problems for Second order Dynamic Equations on Ttime Scales[J].J Math Anal Appl,2004,296(1):97-109.
[2]张英,时间模上四-点边值问题的正解的存在性[J].山西大同大学学报:自然科学版,2014,30(3):1-4.
[3]R I Avery,J Henderson.Two positive Fixed Points of Nonlinear Operators on Ordered Banach spaces[J].Comm Appl Nonlinear Anal,2001,8:27-36.
Existence of Two Positive Solutions to a Four-point Boundary Value Problems on Time Scales
QIAO Shi-dong
(School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi,037009)
In this paper,by using fixed point theorems in cones of Avery and Henderson,we study the existence of at least two positive solutions of a nonlinear second-order four-point boundary value problem for dynamic equations on time scales.
positive solution;boundary value problem;fixed point theorem;time scales;cone
O175.14
A
1674-0874(2015)04-0001-04
2015-01-20
乔世东(1963-),男,山西左云人,硕士,教授,研究方向:代数与方程。
〔责任编辑 高海〕
