改进BP神经网络预测模型实证分析

杨鲁景，武 进，石鹏飞

（成都理工大学管理科学学院，四川成都 610059）

改进BP神经网络预测模型实证分析

杨鲁景，武 进，石鹏飞

（成都理工大学管理科学学院，四川成都 610059）

对BP神经网络进行了简单分析，并针对传统BP网络的缺陷，提出了一些改进的BP神经网络。最后建立基于神经网络的人口预测的模型，用传统BP网络和LMBP网络进行预测对比，结果显示LMBP网络有非常好的预测效果，与传统的BP网络相比有更高的预测精度。

BP神经网络;L-M算法;人口预测

1 BP神经网络

BP(Back Propagation)神经网络，即误差反向传播算法的学习过程，由信息的正向传播和误差的反向传播两个过程组成。当实际输出与期望输出不符时，进入误差的反向传播阶段。误差通过输出层，按误差梯度下降的方式修正各层权值，向隐层、输入层逐层反传。它是在Widrow-Hoff学习算法和ADALINE(ADApive Linear Neuron)网络的基础上针对其单层网络结构只能解决线性可分问题的局限性而提出的。BP神经网络可以用来训练多层网络结构，通过自我学习来调节网络参数从而能够解决复杂的非线性关系的数据分析预测和性能优化问题。

BP算法使用均方误差作为性能指数，并使用最速下降法作为学习规则。算法的输入是一个网络正确行为的样本集合：{p1,t1},{p2,t2},…,{pQ,tQ}。其中pq是网络的输入，tq是对应的目标输出。每输入一个样本，便将网络输出与目标输出相比较。算法将调整网络参数以使均方误差最小化，其均方误差函数F(x)为：

其中，x是网络权值和偏置值的向量。算法通过使用第k次迭代时的均方误差代替均方误差的期望值来近似均方误差的计算，近似均方误差的最速下降算法为：

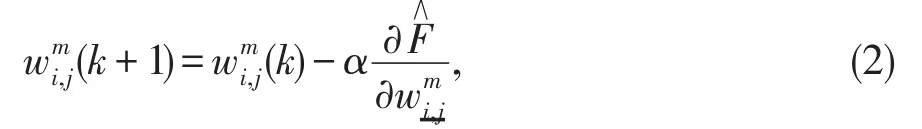
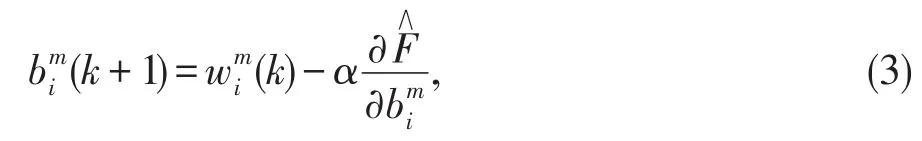
其中,α表示学习速度，m表示神经网络的第m层。

由于均方误差函数F(x)只是网络最后一层权值和偏置值得显式函数，所以为了计算其对网络任意层的权值和偏置值的偏导数，我们引入敏感度的概念。神经元敏感度定义为：

它表示均方误差函数对网络第m层中第i个神经元净输入变化的敏感性。则现在可以将近似最速下降法表示为：

式(5)和(6)给出了使用最速下降法计算权值矩阵wm(k+1)和偏置值矩阵bm(k+1)的表达式，唯一未知的就是敏感度向量sm。假设最后一层为第M层，则可以先求出网络最后一层即第M层的敏感度sM，其矩阵形式为：

然后再用最后一层的敏感度逐一求出前面所有层的敏感度。即敏感度反向传递。敏感度间的递推关系式为：

虽然BP网络得到了广泛的应用，但由于其反向传播算法为最速下降法，自身也存在一些缺陷和不足。主要问题有两个：

首先，由于网络误差曲面在参数空间中的变化很大，在一些区域曲面非常平坦时，我们需要一个大的学习速率，而在区域曲率很高时，需要一个小的学习速率，但算法设定的学习速率是固定的，因此很难为其选择一个合适的学习速率。且BP网络采用的是目标函数的一阶导数信息导致其只具有线性收敛速度，网络的收敛速度较慢，需要较长的训练时间;其次，BP网络使用的是最速下降算法，而最速下降算法是一种局部优化算法，但多层网络结构的目标函数曲面通常比较复杂。BP网络可以使权值收敛到某个值，但这个值可能只是一个局部最小值，不一定是误差平面的全局最小值。

2 改进BP神经网络

由于传统BP算法使用的是最速下降算法，故称其为SDBP(Steepest Descent Back Propagation)算法，其收敛速度比较慢。针对这个问题在实际应用中产生了相应的改进算法。改进的BP算法通常分为两类：启发式方法和标准的数值优化方法。启发式方法主要有：动量方法(MOBP)和改变学习速度方法(VLBP)。MOBP易于实现，并可以用批处理或增量处理模式，但他需要选择动量系统，且r的取值范围限制于[0,1]内，并且算法对它的选择并不敏感。VLBP方法比MOBP快，但只能用批处理方式。所以它需要更多的存储空间。标准的数值优化方法主要有：共轭梯度法(CGBP)和Levenberg-Marquardt方法(LMBP)。CGBP也是一种批处理方法，在每次迭代时要进行线性搜索，速度通常要快于VLBP。LMBP效果最为显著，速度比前面三种改进BP算法都要快。它需要选择两个参数，但算法对参数的选择关系并不敏感。本文采用的即是LMBP算法。

Levenberg-Marquardt算法是牛顿法的变形，用以最小化那些作为其他非线性函数平方和的函数。假设列向量。使用牛顿法作为网络的学习规则，则：

其中，为Hessian矩阵的逆矩阵，gk为梯度。

设误差函数为e(x)，性能函数为误差平方和函数F(x)，则：

其中J(x)为Jacobian矩阵。

Hessian矩阵可以近似表示为

如果假设S(x)很小，可以将Hessian矩阵近似表示为

由此可以得到变形的高斯-牛顿法：

Levenberg-Marquardt算法中的关键一步就是求Jacobian矩阵：假设误差向量为：

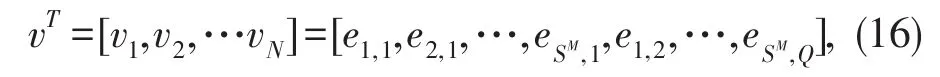
参数向量为：

Jacobian矩阵中的元素可以由BP算法的简单改进计算，由于误差函数只是网络最后一层权值和偏置值的显式函数，我们仍需要引入敏感度概念。由于LMBP算法是将所有输入数据作为一个整体进行处理，故它的敏感度相当于BP算法的敏感度的矩阵增广。最终得到的敏感度增广矩阵间的递推关系表达式为：

LMBP算法不像BP算法那样从输入样本集中一次选择一个输入进行迭代训练，它使用一种批量处理的方式，将数据样本集作为一个整体，当整个训练集都参与计算后网络参数才会更新，这些样本的梯度被平均在一起以或得更精确的梯度估计，从而减少局部收敛的情况。而且LMBP算法采用的是牛顿法的变形，由于引入了Jacobian矩阵，在对网络参数求偏导时使用误差的导数来代替均方误差的导数，使其与BP算法相比具有更快的收敛速度。

3 实证分析

本文选取了中国统计局公布的1993～2013年人口数据。其中1993～2012年这20年的数据作为预测模型的原始数列进行网络训练，用2013年人口数据进行检验。首先，分别用传统的BP算法和LMBP算法建立网络，1993～2012年的数据进行网络训练，网络训练完成后，再用两个训练好的网络分别预测2013年人口数量（见表1与图1）。

表1 BP算法与LMBP算法预测结果

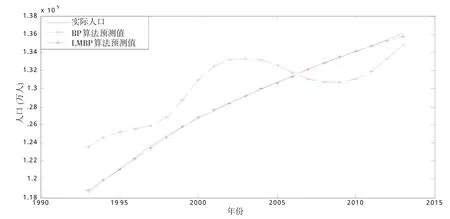
图1 BP算法与LMBP算法预测效果图

从表1可以看出，LMBP网络与原始BP网络相比，有更高的预测精度。从图1可以看出虽然传统的BP网络预测结果反应了预测数据的一定发展趋势，但其预测波动较大，显现出较大的误差，而LMBP网络很好的模拟了预测数据，预测结果很平稳，预测精度也很高。

4 结论

本文通过人口预测的实证分析反应出了传统的BP神经网络预测虽然能体现出人口发展呈增长的趋势，但对于预测人口数量，其误差太大。而LMBP神经网络很好弥补了传统BP神经网络的缺点，其预测的结果非常精确，网络也更稳定。但LMBP神经网络需要存储Jacobian矩阵，所以其存储需求大，同时对于求JTJ矩阵的逆，因该矩阵是n×n的(n是网络中权值和偏置值的总数),如果神经网络中的参数过多，计算将会变得很复杂甚至是难以实现，这些问题都需要进一步的改进和完善。

[1]Martin T，Hagan,Howard B.et al.Neural Network Design[M].北京：机械工业出版社，2002.

[2]闻新，周露，王丹力，等.Matlab神经网络应用设计[M].北京：科技出版社，2000.

[3]李文学,李慧,贺琳.BP神经网络在非线性时间序列预测中的应用[J].长春工业大学学报：自然科学版,2003,24(3)：39-40.

[4]罗东坤,徐平.基于改进BP神经网络的天然气需求预测[J].油气田地面工程,2008,27(7)：20-21.

[5]陶阳威,孙梅,王小芳.基于改进的BP神经网络的中国能源需求预测研究[J].山西财经大学学报,2010,32(2)：3-5.

Empirical Analysis of Improved BP Neural Network Prediction Model

YANG Lu-jing,WU Jin,SHI Peng-fei
(School of Management Science,Chengdu University of Technology,Chengdu Sichuan,610059)

In this paper,the BP neural networks are briefly analyzed,and aiming at the shortage of the conventional BP networks,some improved BP neural network is proposed.Finally,a population prediction model base on neural network is established.The forecast results are compared between the traditional BP network and LMBP network.The results show that LMBP network has very good forecast effect,and compared with the tradition BP algorithm,it has higher forecast accuracy.

BP neural networks;L-M algorithm;population prediction

175.14

A

1674-0874(2015)04-0014-03

2015-04-18

杨鲁景(1991-)，男，苗族，贵州铜仁人，在读硕士,研究方向：基础数学与概率论。

〔责任编辑 高海〕