蜂窝复合材料超声辅助切割工具设计

吴　欣　胡小平　于保华　纪华伟　陆志平　夏晓晴

杭州电子科技大学,杭州,310018

蜂窝复合材料超声辅助切割工具设计

吴欣胡小平于保华纪华伟陆志平夏晓晴

杭州电子科技大学,杭州,310018

在蜂窝复合材料超声辅助切割系统设计中，针对大变幅系数超声变幅杆的设计及其与加工工具配合的问题，基于“代替法”，结合有限元评估技术，建立了超声变幅杆和加工刀具的连接结构设计方法。首先，基于超声辅助加工原理，设计了具有大变幅能力的阶梯-悬链型复合变幅杆。然后，基于“代替法”，研究变幅杆长度减小对变幅杆声学性能的影响规律。进而，基于有限元仿真技术，研究装配后声学系统的声学性能。最后，采用设计的超声辅助切割系统对蜂窝材料进行切割加工实验研究，发现切割面无毛刺，加工过程无粉尘产生，从而验证了设计的超声辅助切割声学系统的有效性。

超声辅助;蜂窝材料;变幅杆;代替法

0　引言

蜂窝复合材料由于具有良好的比强度、比刚度、抗疲劳性能，在航空领域得到了广泛应用。但在蜂窝材料的切割加工过程中,存在加工粉尘大，加工零件表面质量差、尺寸精度低的问题。超声辅助加工工艺是指在蜂窝切割过程中给切割刀具施加耦合超声振动，使刀具与工件材料之间发生间断性冲击与分离，最终使材料发生分离。超声辅助切割工艺可以有效地避免加工粉尘的产生，并且获取高质量的加工表面。

在复合材料超声辅助加工方面，欧洲和美国的各大飞机制造厂和航空复合材料的研发生产企业已将超声切割设备应用于生产。但是，由于国外公司的技术垄断，故针对蜂窝材料的超声辅助切割系统的相关资料极少公开。在国内,虽然对CFRP复合材料[1]、SiCp/Al复合材料等的超声辅助加工工艺进行了一定的研究,但是关于蜂窝复合材料的超声辅助加工的研究较为少见。

蜂窝复合材料切割系统不同于一般的超声辅助加工系统,它需要具备较大的变幅能力，以实现蜂窝复合材料冲击分离的目的。蜂窝复合材料超声辅助切割时，为保证零件加工的质量和效率，工具端部的振幅需要达到20～30 μm,而一般的超声换能器输出振幅为2～3 μm,因此,需要采用具有较大变幅能力的变幅杆以获取满足工程需要的工具振幅。蜂窝复合材料的切割刀具为非规则形状，其结构尺寸和质量相对于变幅杆而言较大,不能简单地简化为一个质量点进行处理，因而，不能简单地以等效质量方法进行变幅杆的设计。切割刀具和变幅杆耦合在一起实现超声系统的机械振动模式和振幅的放大。常规的基于一维波动方程的变幅杆设计方法不能为三维放大结构的设计提供有力的技术支撑。本文结合理论设计方法和有限元分析技术,对大变幅系数超声变幅杆及其与工具的连接部分的设计问题进行了研究。

变幅杆的研究主要集中在常规的变幅杆如高斯型、悬链型和阶梯型变幅杆,其中阶梯型变幅杆具有加工方便、变幅能力强的特点，但同时截面变化部位的应力集中现象也比较明显[2]。此外,随着仿真技术和优化技术的发展,学者们也提出了一些新型的变幅杆。Wang等[3]基于遗传算法,设计了Bazier曲线形状的变幅杆,在实现较大变幅的同时也改善了变幅杆内部的应力分布状况。Roopa等[4]在塑料连接工艺中研究了该变幅杆，得到了较好的结果。另外一种实现较大放大系数的变幅杆是复合变幅杆[5]。

变幅杆和工具耦合在一起时,传统的设计方法往往基于等效质量法,如高斯变幅杆设计时,端部可以采用规则的圆柱进行替代[2]。但是该方法主要是针对工具的质量和尺度都比较小的情况，当工具的尺度比较大时，往往会产生较大的误差。而有限元方法适应性广，具有很强的灵活性，在超声系统性能评估和设计方面应用广泛[6-8]。

因此,本文基于“代替法”，结合有限元评估技术，研究了超声变幅杆和加工刀具的连接结构设计方法及其关键技术。

1　阶梯-悬链复合变幅杆设计

纵波在杆件中传播的波动方程为

(1)

式中,w为圆频率；E为弹性模量;ρ为密度;A为面积;ξ为质点位移。

本文设计的变幅杆分为两段,上半段为λ/4的阶梯型变幅杆,下半段为λ/4的悬链型变幅杆,λ为波长，如图1所示。

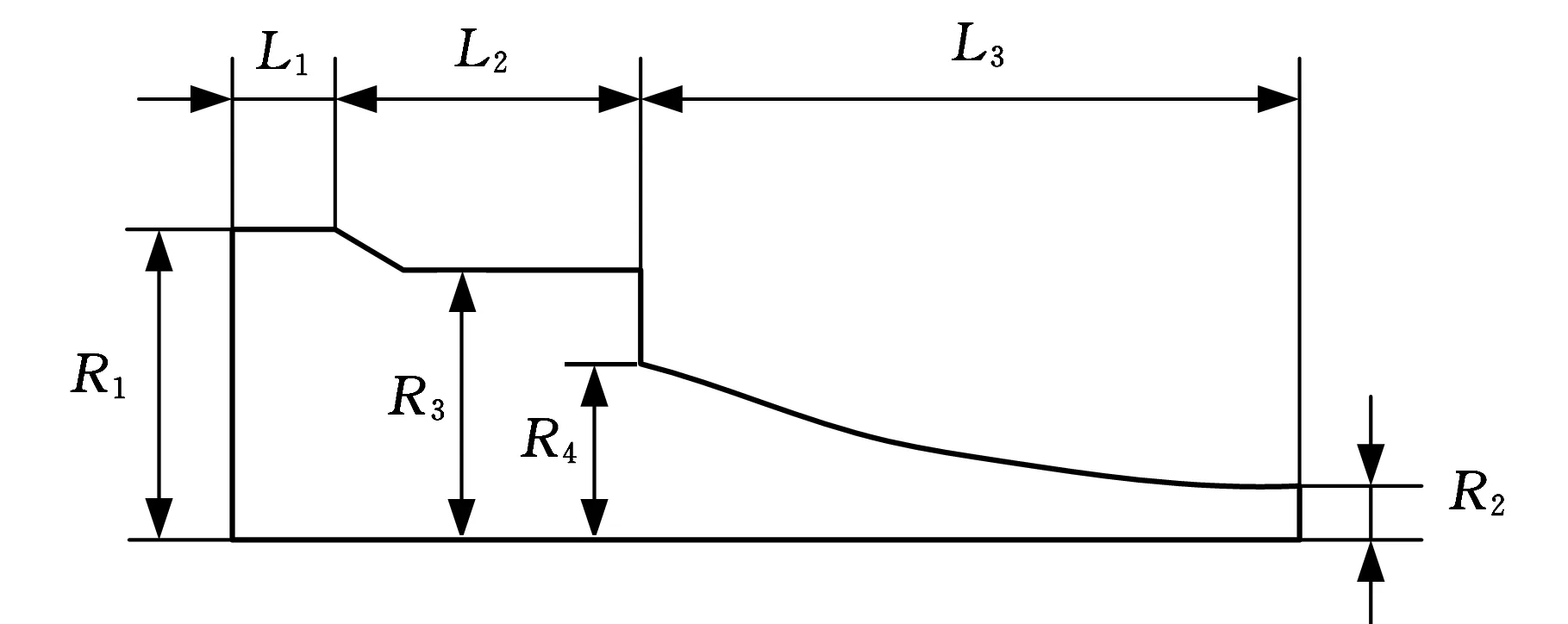
图1　阶梯-悬链复合变幅杆

节点在窄端的四分之一波长的阶梯型变幅杆的频率公式为

cot(kL1)cot(kL2)=S1/S2

(2)

式中,L1、L2分别为四分之一波长变幅杆的大端和小端的长度;S1、S2分别为大端和小端的面积。

根据式(2),选用L1为15 mm,L2为43.6 mm,大端半径为43.5 mm,小端半径为38 mm。

两端自由的四分之一波长悬链型变幅杆长度为

(3)

根据式(3),设置悬链的大端半径为25.5 mm,小端半径为8 mm,计算悬链型变幅杆的长度为94.8 mm。

阶梯-悬链复合变幅杆的相关参数如表1所示。为了与常规变幅杆的性能进行对比,设计了单一悬链型变幅杆，相关参数如表1所示。

表1　阶梯-悬链复合变幅杆结构参数

2　基于“代替法”的变幅杆与加工工具耦合设计

蜂窝材料切割刀具为一个非规则结构的刀片,如图2所示。当超声变幅杆耦合了切割刀具后,整个系统的纵振频率、节点和放大系数会发生变化。因此,本文采用“代替法”设计变幅杆与工具的连接，即在变幅杆的端部截去一部分，取而代之的是加工工具，如图3所示。由于切割刀具形状复杂，采用理论分析较为困难，因此，结合有限元分析技术,动态调整分析模型的几何尺寸,系统分析耦合后的声学系统的性能。

图2　加工刀具图3　代替法示意图

2.1超声辅助切割系统加工工具设计

超声辅助切割系统加工工具由刀具和支座构成。刀具座具有支撑刀具和与变幅杆连接两个功能，因此材料采用与变幅杆性能相差不大的钢材。刀具选用硬质合金，硬质合金刀具的弹性模量和密度都比较大,在振动的过程中相当于一个质量块，因此对刀具座与变幅杆的连接具有较高的要求。如果采用刚度和硬度都比较小的钛合金,可能出现刀片横向摆动,从而导致切割时刀具不锋利的现象出现。

2.2变幅杆截去后的性能分析

首先分析变幅杆尺寸调整后的性能数据，即研究长度缩短后变幅杆的振动特性。采用FEMAP前处理软件中的模型特征编辑命令可以方便地修改变幅杆的长度。通过NXNASTRAN分析，得到随变幅杆的长度减小,变幅杆放大系数和纵振频率的变化规律。

从图4中可以看到,随着四分之一波长的悬链变幅杆的长度减小,复合变幅杆的纵振频率线性增加。从图5中可以看出,变幅杆的放大系数随其长度的减小而逐渐减小。在研究的范围内，超声变幅杆的声学性能基本呈线性变化。

图4　纵振频率随长度的变化规律

图5　放大系数随长度的变化规律

2.3整体声学系统性能评估

刀具和变幅杆耦合在一起后，结构的性能将会发生显著变化,因此,采用有限元技术虚拟评估耦合在一起的切割工具的振动特性。首先，将工具耦合到分析模型中，分析整体系统的动力学性能。然后通过调整变幅杆的长度得到整体的声学系统性能。基于有限元分析结果，设计复合变幅杆中的悬链部分的杆件长度由94.84 mm减小为79.84 mm。

有限元分析结果表明，整体声学系统的放大系数为9.765,比原先的复合变幅杆的放大系数9.66稍大。分析其原因,认为刀具为薄片状,导致整体声学系统的长度为180.6 mm,要大于初始设计的变幅杆的长度153.6 mm,所以刀尖的振幅有所增大。

基于有限元方法计算得到整体声学系统的纵振频率为19.74 kHz。超声电源的工作频率设计为20 kHz,模型的纵振频率与设计频率的相对误差为1.3%,满足设计要求。

图6所示为超声声学系统19.74 kHz下的纵振模式。图7给出了超声声学系统在19.74 kHz纵振模态下沿变幅杆轴线方向节点的相对位移。该节点位移不是变幅杆在激振下的真实振幅。但是根据模态计算原理，该位移为系统在谐振状态下结构各点振幅相对于基准点变换后的相对位移,因此,该曲线可以认为是在19.74 kHz激振频率下,结构沿变幅杆轴线方向振幅的相对变化规律。

图6　超声声学系统19.74 kHz下的纵振模式

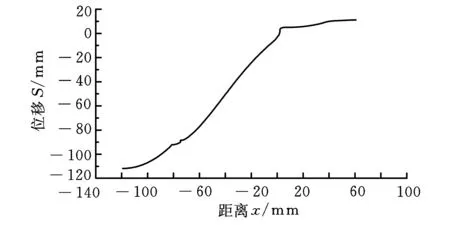
图7　19.74 kHz纵振模式下沿变幅杆轴向上节点的位移曲线

变幅杆节点处的振幅为零。从图7中可以看到：当x=1.5 mm时,计算得到的位移为0，该处即为仿真得到的节点。曲线中的横坐标为变幅杆轴向方向，坐标为零(x=0)处是切割刀具结构设计的节点，该处计算得到的位移为-3 mm,该位移相对于端部120 mm的位移而言非常小。可见，设计的节点位置和计算得到的节点位置相差不超过1.5 mm。

此外，一般变幅杆的节点处需要加上一个支撑法兰，该支撑法兰厚度在理论上认为越薄越好，但是在工程应用中,一般为1～3 mm,以保证支撑法兰的刚度，而设计的节点位置和仿真得到的节点位置偏差仅为1.5 mm,所以,可以认为设计的变幅杆节点位置与计算得到的节点位置基本吻合。

3　加工刀具几何结构和材料参数对声学系统稳健性的影响

超声声学系统的设计中可控因素为产品的几何结构，不可控因素是材料的性能参数如材料的弹性模量和密度。因此，本文主要研究刀具的弹性模量发生的微小变动对结构的纵振的频率、模式和放大系数的影响规律，即结构性能对材料弹性模量的敏感程度。

3.1变幅杆加工对称性对超声声学系统性能的影响

当变幅杆加工精度较低时,如变幅杆结构的对称性较差,结构振动时,薄片状结构切割刀具会因弯曲刚度不足而发生摆动。该摆动现象会导致刀片切割材料时发生过度摩擦现象,严重时发生刀片断裂现象。

为了表现变幅杆关于刀片中面的非对称性,对变幅杆一侧细分网格,另一半划分粗糙网格。当模型网格对称时(图8a),刀具具有较好的纵振模式。而当变幅杆的对称性较差时(图8b),刀片具有明显的弯曲模式。因此，加工变幅杆时需要注意其对称性，以保证刀具的寿命。

(a)对称性较好(b)对称性较差图8　变幅杆对称性对纵振模态的影响

3.2刀具材料性质波动对超声声学系统的影响

硬质合金多为钴(Co)镍(Ni)合金,不同的牌号材料性质相差较大。表2给出了刀具材料密度为14.81×103kg/m3,取不同的弹性模量值时，计算得到的变幅杆纵振频率和放大系数。由表2可以发现当刀具的弹性模量发生变化时，声学系统的纵振频率基本不发生变化，而放大系数会有一定的变化。在研究的弹性模量取值范围内，当弹性模量有10%的变化时，放大系数仅有1%的变化。所以,在弹性模量的取值范围内,可以认为刀具弹性模量的变化对声学系统的影响较小。

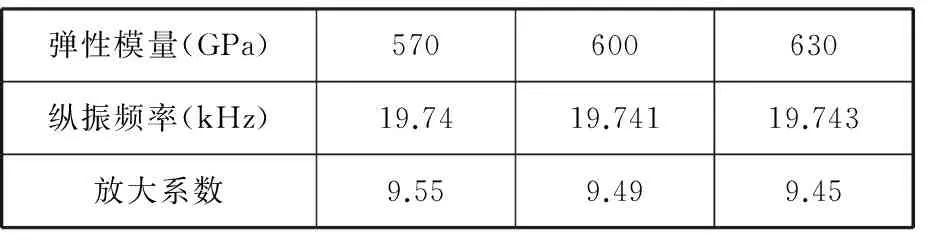
表2　刀具不同弹性模量时的声学系统纵振频率

4　超声辅助切割过程实验研究

4.1超声辅助切割系统纵振频率测试

为了使变幅杆能够固定在工作台架上,在变幅杆节点处增加了支撑结构，进而采用数控加工的方式，加工出设计的蜂窝复合材料切割系统,如图9所示。

图9　超声辅助切割声学系统

对加工的超声辅助切割系统进行相关数据的采集。利用型号为TH2818的同惠元件分析仪测试变幅杆和装配好的切割工具的声学系统的纵振频率，测试结果如图10所示。

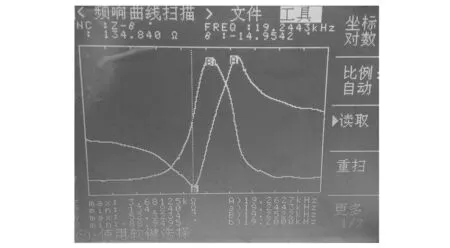
(a)变幅杆纵振频率

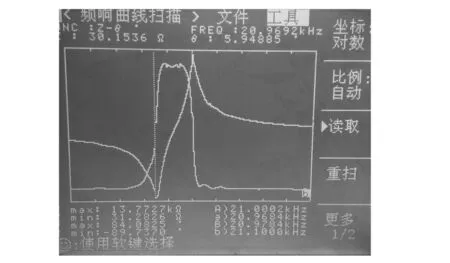
(b)声学系统纵振频率图10　变幅杆和整个声学系统纵振频率测试

变幅杆的纵振频率和耦合加工刀具之后的纵振频率分别为20.97 kHz和19.24 kHz,而采用有限元设计计算的频率分别为21.4 kHz和19.74 kHz,两者相对于实验测试数据的相对误差分别为1.9%和2.6%。误差产生的原因为：一方面可能是加工变幅杆的曲线形状具有一定偏差，另一方面取用的材料参数可能有所偏差。

4.2蜂窝复合材料切割实验

采用设计的超声辅助切割平台对蜂窝复合材料进行切割实验。

超声辅助加工过程中,换能器输入功率为0.12kW,工作频率为19.2kHz。刀尖部位的振幅难以测量，因此，对变幅杆端部的振幅进行了测量，变幅杆端部振幅为17 μm。切割时，将蜂窝材料粘到工作台上，工作台采用伺服驱动进给,实验装置如图11a所示。

切割后的蜂窝复合材料表面如图11b所示。蜂窝材料的切割过程是一个粗加工过程，对加工零件的表面加工精度没有细致要求,仅要求加工表面没有明显毛刺。而从图11b中可见,蜂窝复合材料的切割平面光滑,没有明显毛刺产生,满足蜂窝复合零件加工要求。

(a)加工过程(b)加工表面图11　切割蜂窝复合材料实验

此外,当不耦合超声振动进行切割时，由于需要的切割力较大，材料较为难以切割，并且切割过程中会有粉尘产生。因此，设计的超声辅助切割系统不仅可以有效地减少加工过程产生的粉尘,而且可以大幅减小加工过程中的材料切割力。

在材料切割过程中存在变幅杆温升较高的现象,这意味着变幅杆和切割刀具之间存在着一定的阻抗匹配问题，这也是下一步研究的重点问题。

5　结论

本文针对蜂窝复合材料的加工过程，基于超声辅助加工原理，设计了超声辅助加工声学系统。针对大变幅系数超声变幅杆与加工工具配合的问题，基于“代替法”，结合有限元评估技术，建立了超声变幅杆和加工刀具的连接结构设计方法。采用设计的超声辅助切割系统对于蜂窝材料进行切割加工实验研究，研究过程表明：

(1)阶梯-悬链复合变幅杆具有10倍振幅放大能力，而同样截面尺寸的悬链变幅杆的放大系数为4.9。

(2)提出了基于代替法和有限元评估技术的变幅杆和工具耦合设计方法，设计了满足要求的超声辅助切割系统。

(3)蜂窝复合材料切割实验研究表明,超声辅助切割工艺可以实现快速高质量的蜂窝复合材料切割，并且加工过程无粉尘产生。

(4)在蜂窝复合材料切割实验中发现超声变幅杆部位存在较大温升现象，该问题是下一步研究重点。

[1]马付建. 超声辅助加工系统研发及其在复合材料加工中的应用[D]. 大连: 大连理工大学, 2013.

[2]林仲茂.超声变幅杆的原理和设计[M]. 北京: 科学出版社, 1987.

[3]Wang D A,Nguyen H D.A Planar Bezier Profiled Horn for Reducing Penetration Force in Ultrasonic Cutting [J]. Ultrasonics, 2014, 54(1): 375-384.

[4]Roopa Rani M, Rudramoorthy R. Computational Modeling and Experimental Studies of the Dynamic Performance of Ultrasonic Horn Profiles Used in Palstic Welding[J]. Ultrasonic,2013,53(3):763-772.

[5]张可昕. 基于有限元的超声复合变幅杆的动力学分析及优化设计[D]. 北京：北方工业大学, 2012.

[6]Lucas M,MacBeath A,McCulloch E,et al.A Finite Elment Model for Ultrsonic Cutting[J].Ultrasoincs, 2006, 44: 503-509.

[7]Kuo K L. Ultrasonic Vibrating System Design and Tool Analysis[J]. Transactions of Nonferrous Metals Society of China, 2009,19(S1): 225-231.

[8]冯冬菊,赵福令,徐占国.使用Inventor软件的超声变幅杆模态分析[J].应用声学,2010,29(1):69-73.

Feng Dongju,Zhao Fuling,Xu Zhanguo.Modal Analysis of Ultrasonic Horn Using theInventor Software[J].Applied Acoustics,2010,29(1):69-73.

(编辑袁兴玲)

Design of Ultrasonic Cutting Tool for an Ultrasonic Assisted Cutting Process of Nomex Honey-comb Materials Based on Substitution Method

Wu XinHu XiaopingYu BaohuaJi HuaweiLu ZhipingXia Xiaoqing

Hangzhou Dianzi University,Hangzhou,310018

A substitution method under help of the finite element method was proposed to solve the problem of the coupled design of a composite horn and the cutting tool of an ultrasonic acoustic system for the noomex honeycomb material cutting process.First,a stepped-catenoidal composite horn with high displacement amplification factor was designed by using the theory of elastic wave propagation and finite element analysis technique.Then,the influences of the horn length on the vibration characteristics were studied based on substitution method using finite element method.The performance of the ultrasonic vibration system was studied by using finite element method.Finally,the ultrasonic acoustic system was fabricated and the ultrasonic assisted cutting experiments were performed,and the nomex honeycomb materials were cut effectively by using the designed system.The machined surface shows high surface quality which is smooth without burrs.Thus,the effectiveness of the designed cutting tools was demonstrated.

ultrasonic;nomex;horn;substitution method

2014-03-17

国家自然科学基金资助项目(KYZ013710037);中国博士后科学基金资助项目(2013M541769)；国防科工局重大专项(A3920133001)；浙江省自然科学基金资助项目(LY14E050025)

TH136DOI：10.3969/j.issn.1004-132X.2015.06.019

吴欣，男，1979年生。杭州电子科技大学机械工程学院讲师、博士。主要研究方向为材料成形过程仿真技术。发表论文10余篇。胡小平，女，1971年生。杭州电子科技大学机械工程学院教授。于保华，男，1978年生。杭州电子科技大学机械工程学院工程师、博士。纪华伟，男，1976年生。杭州电子科技大学机械工程学院副教授、博士。陆志平，男，1974年生。杭州电子科技大学机械工程学院高级工程师。夏晓晴，女，1989年生。杭州电子科技大学机械工程学院硕士研究生。