光刻旋涂中的膜厚分析与数值模拟

刘学平　郑　钢,2

1.清华大学深圳研究生院,深圳,518055　　2.清华大学,北京,100084

光刻旋涂中的膜厚分析与数值模拟

刘学平1郑钢1,2

1.清华大学深圳研究生院,深圳,5180552.清华大学,北京,100084

旋涂法是光刻工艺中涂胶的重要方法,在旋涂经典EBP方程和考虑挥发与转速关系的溶剂挥发模型基础上，通过数值模拟对溶剂挥发模型提出的过渡点增加了动态参数因子补偿，得出更合理的膜厚拟合方程。通过自制的旋涂验证装置进行光刻涂胶实验并采集相关实验数据来验证拟合方程的正确性。利用该优化的拟合方法来指导实践,可制定更为合理的实际工艺参数。

旋涂；动态补偿因子；溶剂挥发；膜厚

0　引言

典型的旋涂过程主要分为滴胶、旋转匀胶和溶剂挥发三个步骤。首先，将旋涂液滴滴到基片表面上,然后通过高速旋转将液滴铺展开来，形成均匀薄膜，再干燥蒸发掉剩余的溶剂,最后便得到性能稳定的薄膜。旋涂法是重要的工业技术,它具有工艺简单、成本低廉、操作简单等优点，因而在工业很多领域都有应用。在硅片晶圆上采用旋涂工艺涂覆光刻胶是制作集成电路芯片的重要环节。随着信息技术智能化的发展,芯片的制造愈发重要,研究旋涂工艺具有重要的意义。

对于旋涂工艺，Emile等[1]研究了牛顿流体在旋转圆盘上的运动,范椿[2]和陈春芳[3]研究了黏塑性流体在旋转圆盘上的运动。旋涂过程比较复杂,涉及许多物理化学过程,如润湿、扩散、流体流动、挥发等[4]。在对旋涂工艺的研究中，Meyerhofer[5]第一次考虑了挥发因素，并推导出初略估计最终膜厚的方程。近年来CD-R/DVD-R作为记录信息的载体得到大力发展，所涉及的染料旋涂过程时间非常短，膜厚大概为几十纳米,对转速的要求也非常高,一般不小于5000 r/min，文献[6]在考虑挥发的基础上对挥发因子进行了修正,但其修正系数为常数，与转速无关。通常的旋涂光刻胶工艺膜厚约为几百纳米到几微米,时间周期40 s左右,旋转速率无需染料旋涂那么高，但其膜厚数值分析原理仍具有一定的借鉴意义。本文采用补偿与转速相关的动态挥发因子,来修正膜厚拟合求值公式并进行实验验证。

1　EBP方程及Meyerhofer分析模型

对于旋涂模型,Emile等[1]总结出了牛顿流体的分析模型(称作EBP方程),它假定旋转盘无限大，流体在其表面的流动径向对称,重力和科氏力忽略不计，同时也忽略溶剂挥发和自由表面的剪切力,也假定流体仅在其径向存在剪切阻力。最终得出牛顿流体厚度方程为

(1)

式中，h代表与径向位置r相关的液体随时间变化的高度;h0为t=0时与径向位置r相关的液体高度;ω为转盘旋转角速度;υ为流体运动黏度；t为时间。

由式(1)可推出高度变化率为

(2)

α=ω2/(3υ)

式(2)是不考虑挥发情况下的牛顿流体的高度随时间的变化,Meyerhofer首次提出在旋涂分析过程中增加挥发因素[5],设由挥发引起的高度变化率(简称为挥发率)为e，则式(2)变为

(3)

假定溶液的溶质浓度a是均一稳定的,总溶液的体积等于溶剂和溶质的体积之和,现定义S和L是单位体积内的溶质和溶剂的高度,则对于单位面积内的溶质和溶剂的体积亦为S和L，则溶质浓度为

a(t)=S/(S+L)

(4)

单位面积内的溶液总高度h应为溶质和溶剂的高度之和,即

h=S+L

(5)

由式(2)～式(5)可得溶质的扩散方程为

(6)

(7)

在一定实验环境下,溶剂挥发与转速[7-8]有如下关系式：

(8)

其中,c为特定环境下转速参数,所以式(7)化为

(9)

式(1)～式(9)没有解析解,Meyerhofer则进一步假设,把旋涂过程分为三个过程:第一个是低速下料阶段,溶液滴在低速旋转的旋转盘上,此时离心力占主导地位,溶液在离心力的作用下快速往外铺开;第二个是忽略挥发的中速扩散阶段，液体径向外流，逐步形成均匀的薄层；第三个是高速挥发阶段，这个阶段，液体层已经变得很薄，向外径向流体基本忽略不计，主要是溶剂的挥发占主导。设从第二阶段到第三阶段的过渡点为T点，在T点之前忽略挥发,过渡点之后考虑挥发的效应，在过渡点处则满足挥发率e等于径向流动效应造成的溶剂高度变化率H,即在过渡点T处有

e=H

(10)

从这点之后径向流动可以忽略不计,设T点处的膜厚为hT,最终膜厚hf为

(11)

式中,a0为初始溶液的溶质浓度；υ0为流体初始运动黏度。

染料旋涂的理论分析中对式(10)已进行了补偿,其补偿的条件是所有转速下溶剂挥发率e是固定不变的，但是实际溶剂挥发率e与角速度ω满足关系式(8)。即挥发率不是固定的，是与转速相关的，在过渡点T处挥发率与径向流动效应造成的溶剂高度变化率的关系并不是直接相等，需要增加动态补偿因子,设补偿因子为α1(ω),则

e=α1(ω)H

(12)

(13)

2　修正挥发因子

2.1通过数值仿真确定修正系数α1(ω)

根据之前理论分析，将式(6)、式(9)进行数值仿真，首先将其离散化，得到离散化的方程：

旋涂工艺中,设定初始参数为:h0=30 μm,a0=0.05,υ=(10-6+a4)m2/s,e0=1×10-7m/s,c0=6.91×10-9m/s,ω=209.33 rad/s(n=2000 r/min),代入上面两个离散化方程。取Δt=0.01,步数为4000步，分别取转速n为3000 r/min、2500 r/min、1500 r/min，用两离散方程得出溶质和溶剂的厚度变化曲线，如图1～图3所示。

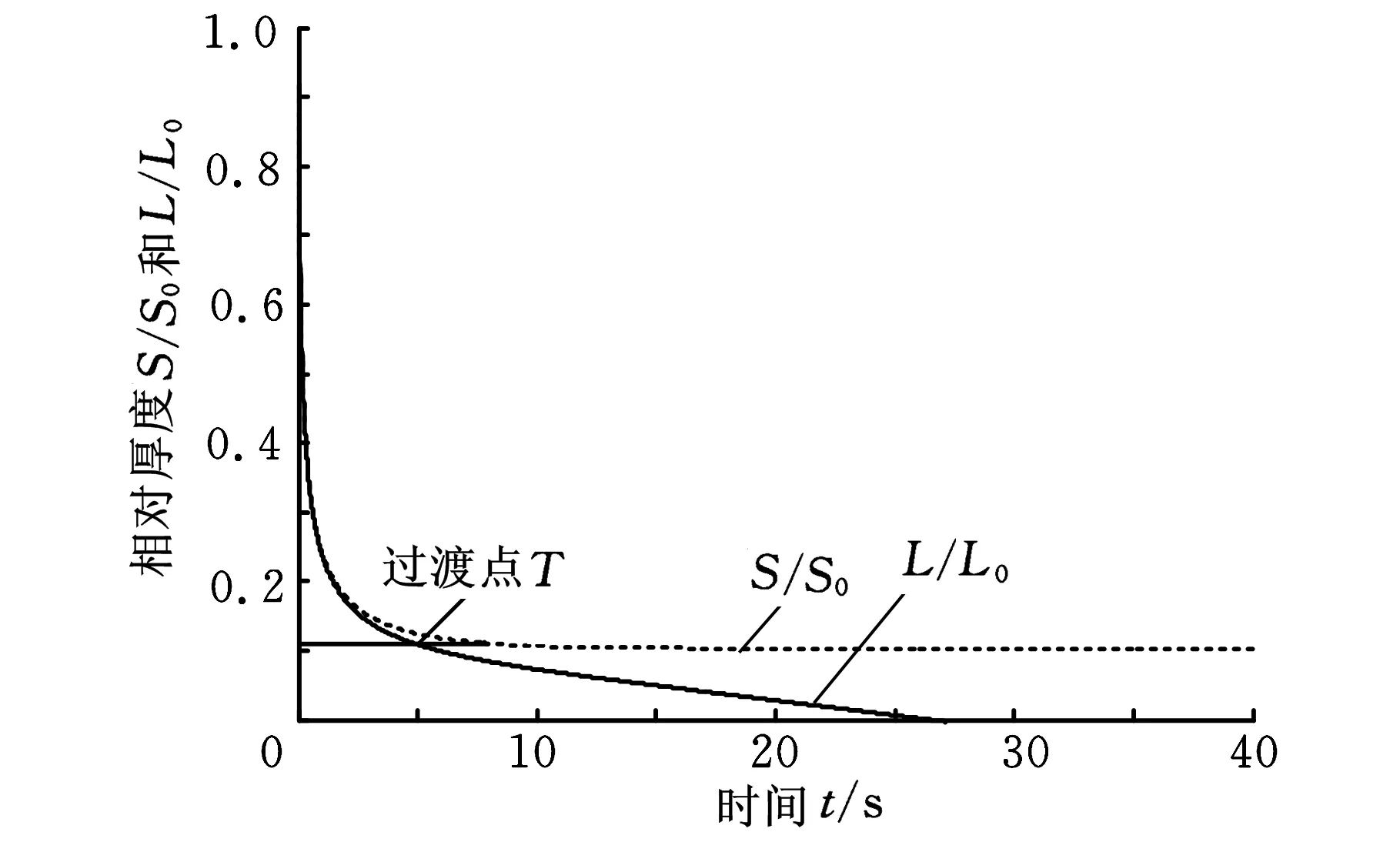
图1　转速n=3000 r/min时溶质和溶剂相对膜厚随时间变化

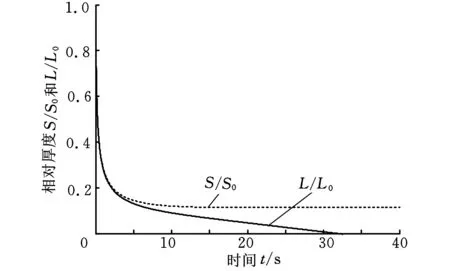
图2　转速n=2500 r/min时溶质和溶剂相对膜厚随时间变化

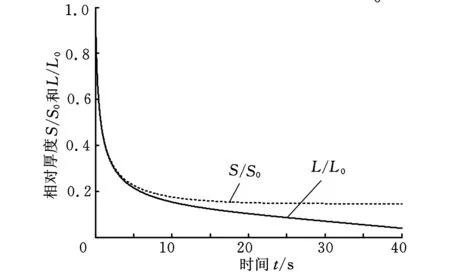
图3　转速n=1500 r/min时溶质和溶剂相对膜厚随时间变化

S/S0表示溶质的相对厚度,L/L0表示溶剂的相对厚度。由仿真曲线图1～图3可知旋涂过程可分为3个阶段：第一阶段离心力占主导作用，流体逐步外流，铺满整个晶圆，形成厚度为h0的薄膜；第二阶段液体紧贴边界的极薄层与固体边界之间没有相对运动，即液体与固体间无摩擦力,所以液体的摩擦力主要表现为液体内部层与层之间的摩擦力,称为牛顿内摩擦力，正是因为牛顿内摩擦力的存在，越远离固体边界层的液体流速就越快(图4)，此阶段液体外层逐步往外扩散流动开,最终黏滞力与离心力达到平衡，晶圆表面形成均匀膜厚，此过程中带有一定的挥发;第三阶段没有径向流动,只是剩余溶剂的大量挥发，最后表面剩下均匀干燥的薄膜。

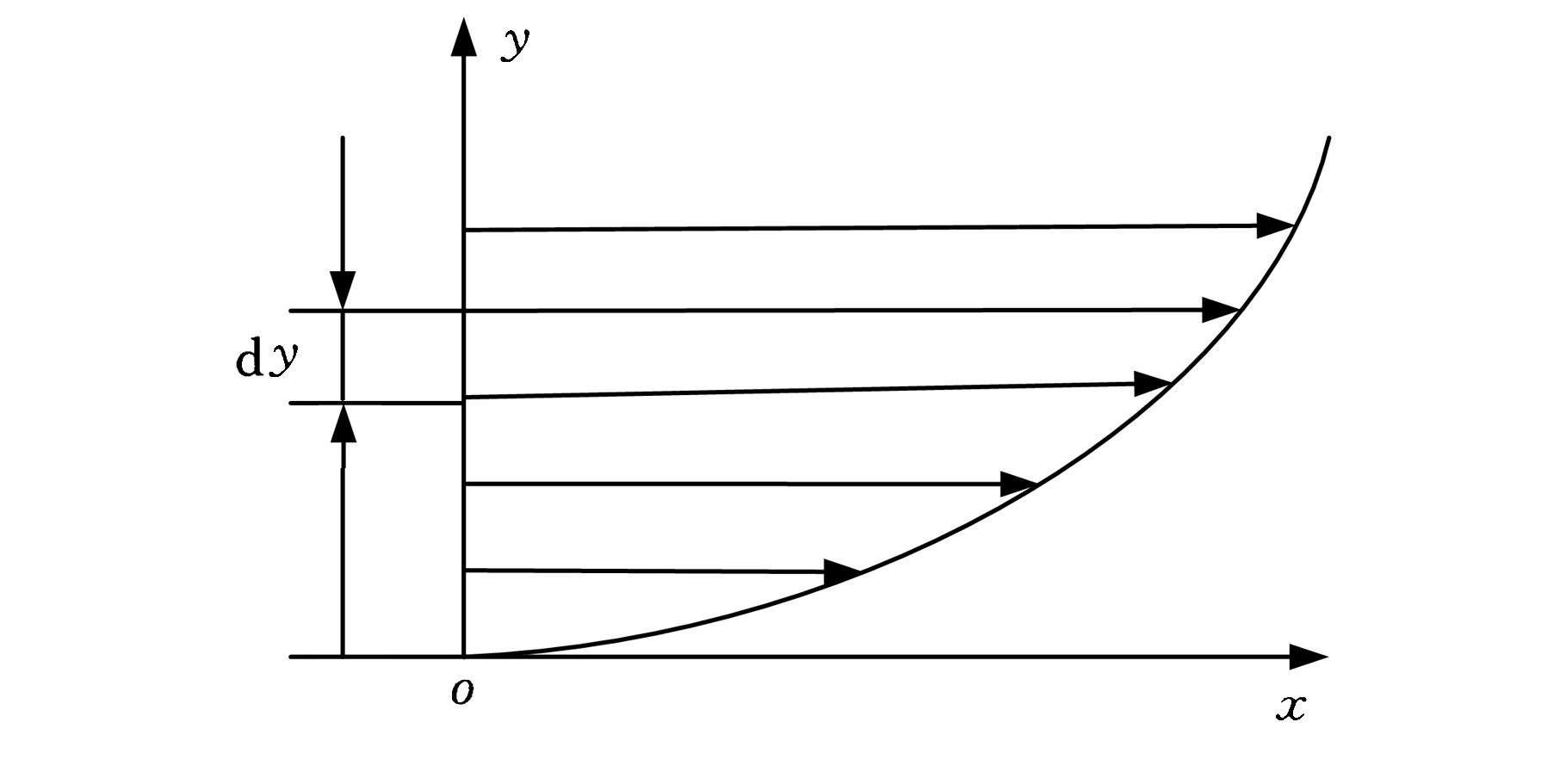
图4　流体速度梯度

通过MATLAB将4000个点的坐标值输出得到数据表1(只显示部分数据)。对图1和表1数据进行分析，S/S0从第1000个点开始溶质的膜厚基本不变了,可取S/S0曲线的第1000到1500点进行数据计算,根据Meyerhofer假设,过度点T之前径向外流过程无挥发,那么此时溶剂相对膜厚与溶质相对膜厚相等，即L/L0=S/S0,当S/S0曲线斜率基本不变时,此时溶剂相对厚度L/L0曲线纵坐标上与S/S0相等的点即为转折点T,由图1找出转折点T大致位于第550到650个点之间,由于此区间内斜率变化不大,故可由第550点和650点两点确定T处斜率。再从表1上找到两点对应的数值，由图1和表1对应的数值可得过渡点实际溶剂斜率为

挥发率为

e=kL

过渡点实际溶质斜率为

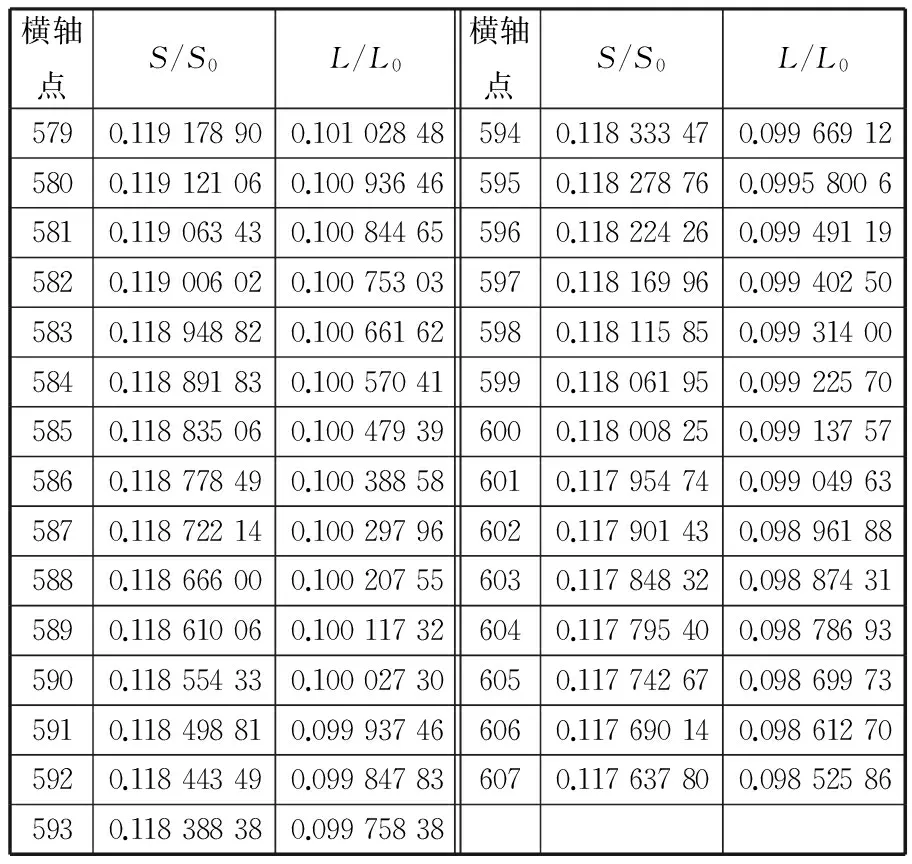
表1　转速n=3000 r/min时溶质和溶剂相对膜厚变化分布点(部分)

忽略挥发时,由式(6)、式(7)得溶剂斜率与溶质斜率比例系数:

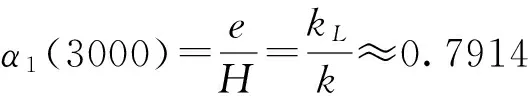
e=α1(3000)Hα1(3000)=0.7914

采用同样的方法得出n=2500 r/min时的修正系数α1(2500)=0.7372。故过渡点T处的挥发率近似修正为:e=α1(2500)H。n=1500 r/min时的修正系数α1(1500)=0.537。故过渡点T处的挥发率近似修正为:e=α1(1500)H。

2.2实验验证

为了得到实验数据，我们搭建了运动旋涂实验装置，装置如图5所示。实验中用的光刻胶为AZ4999,它的主要溶剂成分为丙二醇甲醚醋酸酯和丙酮，丙酮含量大于85%(体积分数)，丙二醇甲醚醋酸酯含量约5%。实验中采用直径为1.5 mm的滴管来滴取光刻胶。使直径为304.8 mm(12英寸)的晶圆在不同转速下旋涂AZ4999光刻胶,测量出最后的膜厚数据来验证补偿法的可行性。膜厚的测量仪器是NanoCalc光学薄膜厚度测量系统,它是利用薄膜反射干涉的原理对薄膜进行厚度测量以及分析，其测量范围可以达到10 nm～250 μm,可以同时完成多达3层膜厚的测试。

图5　旋涂实验装置

数据采集是从晶圆边沿到晶圆中心等距离的取出6个点,然后在距离中心的某点环绕一周测量6个点来记录数据,其中a点是靠边沿处，f点是晶圆中心及附近(图6)。表2和表3是通过膜厚仪在不同转速下测量出来的膜厚数据。

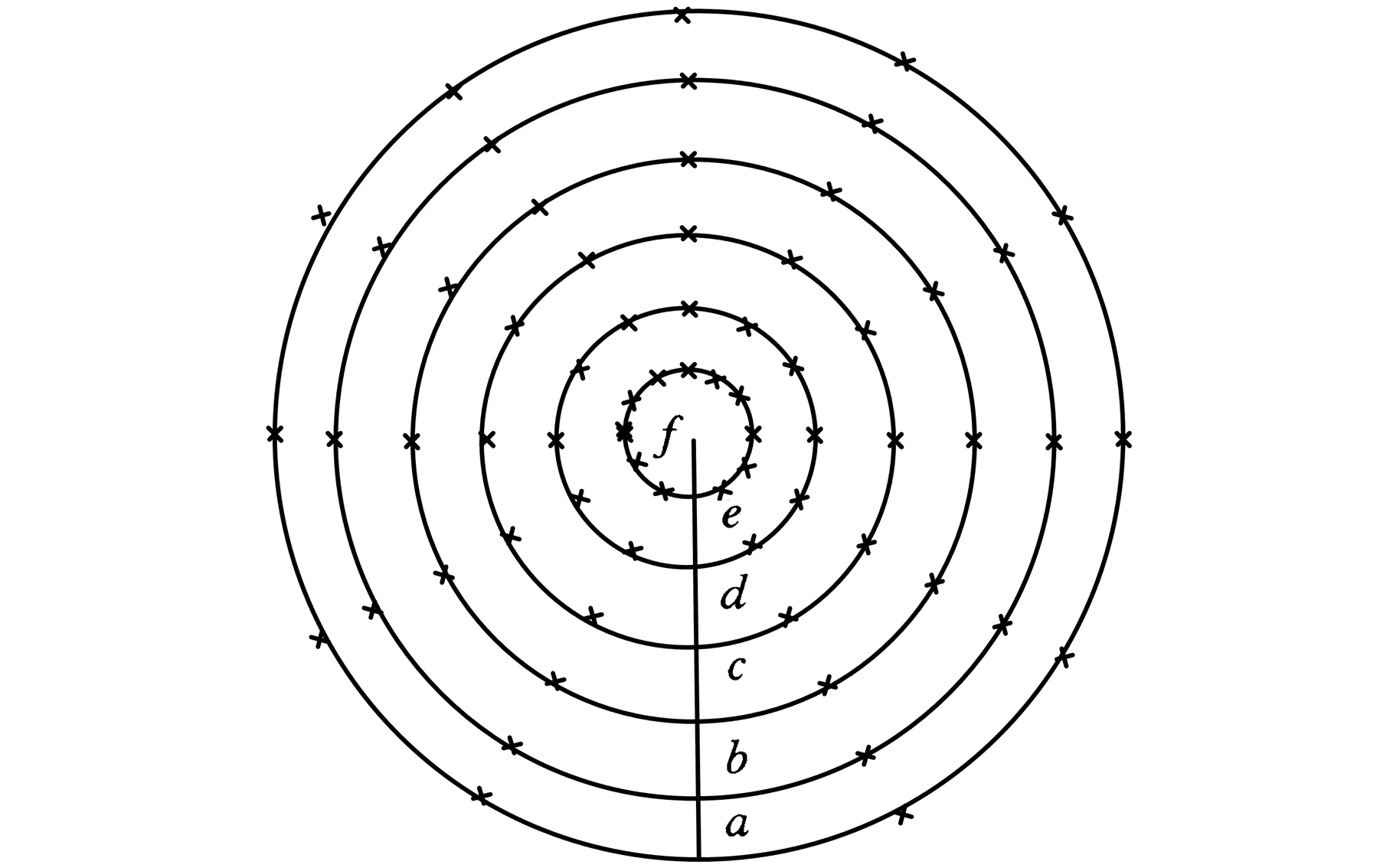
图6　数据采集示意图

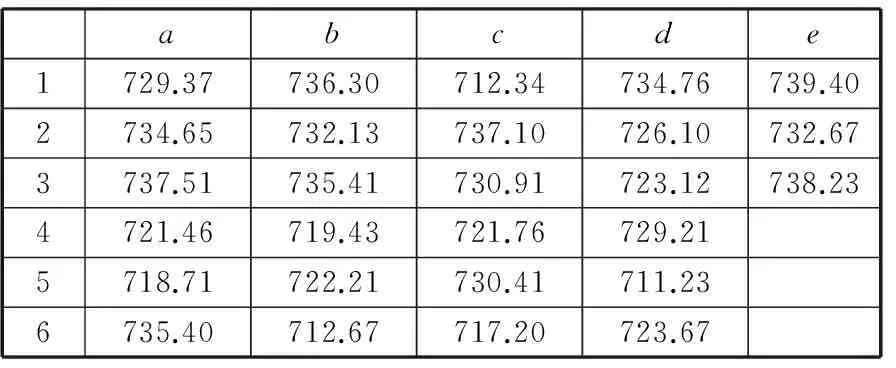
表2　转速为1500 r/min时采集的数据　nm

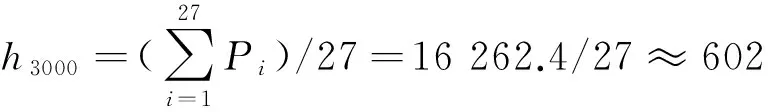
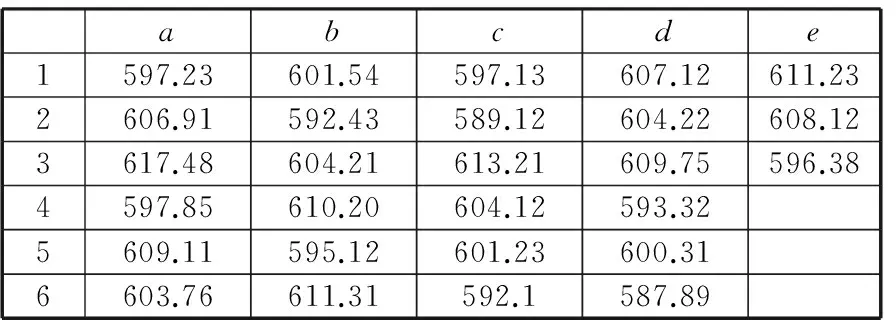
表3　转速为3000 r/min时采集的数据　nm

依据之前的修正值,n=3000 r/min时e=α1(3000)H,α1(3000)=0.7914;n=2500 r/min时e=α1(2500)H,α1(2500)=0.7372;n=1500 r/min时e=α1(1500)H,α1(1500)=0.537。由于膜厚拟合方程中一些参数是设定的，不方便直接求出最终膜厚，故将转速为1500 r/min得到的平均膜厚作为基准来对比。

根据式(11),未修正数据前，最终膜厚比值为

根据式(8)和式(13)将修正参数代入,则有最终膜厚比值：

而实际膜厚比值为

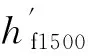
由上述数据可知公式e=α1(ω)H中,补偿α1不是一个固定值,而是与旋转角速度ω相关。

3　结论

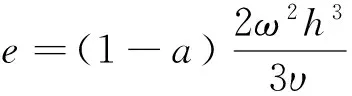
[1]Emslie A G,Bonner F T,Peck L G.Flow of a Viscous Liquid on a Rotating Disk[J].J. Appl. Phys.,1958,29(5):858-862.

[2]范椿.粘塑性流体在旋转圆盘上的流动[J].应用数学和力学,1994,15(5):421-427.

Fan Chun.The Flow of Viscoplastic Fluid on a Rotating Disk[J].Applied Mathematicsand Mechanics,1994,15(5):421-427.

[3]陈春芳.非牛顿流体的一些本构方程[J].力学学报,1983,15(1):16-26.

Chen Chunfang.Some Constitutive Equation of Non-Newtonian Fluid[J].Chinese Journal of Theoretical and Applied Mechanics,1983,15(1):16-26.

[4]王东，刘红缨,贺军辉,等.旋涂法制备功能薄膜的研究进展[J].影像科学与光化学,2012,30(2):91-101.Wang Dong,Liu Hongying,He Junhui,et al.The Progress of Research on Functional Thin Films Manufactured by Spin Coating Method[J].Imaging Science and Photochemistry,2012,30(2):91-101.

[5]Meyerhofer D.Characteristics of Resist Films Produced by Spinning [J].J. Appl. Phys.,1978,49:3993-3997.

[6]岳宏达,潘龙法,徐端颐.染料旋涂工艺的挥发和流动[J].清华大学学报(自然科学版),2004,44(2):174-177.

Yue Hongda,Pan Longfa,Xu Duanyi.The Evaporation and Flow of Dye Coating Process[J].J. Tsinghua Univ. (Sci. & Tech.),44(2):174-177.

[7]Jamal M S.流体流动手册[M].北京:中国石化出版社,2004.

[8]Kreith F,Taylor J H,Chong J P.Heat and Mass Transfer From a Rotating Disk[J].Journal of Heat Transfer May,1959,81:95.

(编辑袁兴玲)

Analysis and Numerical Simulation of Film Thickness of Photoresist Spin Coating

Liu Xueping1Zheng Gang1,2

1.Graduate School of Tsinghua University at Shenzhen,Shenzhen,Guangdong,518055 2.Tsinghua University,Beijing,100084

The spin coating method was an important method for photoresist coating in the photolithography process.Based on the mode of the classical EBP equation and solvent evaporation mode which considered the relationship between the solvent evaporation and spin speed,and the dynamic parameter compensation was added through the numerical simulation of the transition point to get a further modified equation. The validity of the modified equation was verified by the experimental data collected by the lab made spin coating device. More reasonable process parameters can be obtained with this optimized fitting method.

spin coating;dynamic compensation factor;solvent evaporation;film thickness

2014-02-04

国家科技重大专项(2012ZX02102)

TQ630.6DOI：10.3969/j.issn.1004-132X.2015.06.005

刘学平,男,1965年生。清华大学深圳研究生院先进制造学部副研究员。主要研究方向为机电控制、绿色设计与绿色制造。获省部级科技进步一等奖1项,发表论文30余篇。郑钢,男,1989年生。清华大学精密仪器与机械学系硕士研究生。