基于参数识别的截割头纵向随机振动响应优化
2015-10-29李晓豁沙永东
李晓豁 何 洋 焦 丽 沙永东 李 婷
辽宁工程技术大学,阜新,123000
基于参数识别的截割头纵向随机振动响应优化
李晓豁何洋焦丽沙永东李婷
辽宁工程技术大学,阜新,123000
为减小纵轴式掘进机截割头的振动,利用Lagrange方法并结合虚拟激励法推导了该型掘进机的纵向运动微分方程,根据Daubechies小波函数多尺度逼近方法和最小二乘法原理,将掘进机在随机激励作用下系统的时变阻尼和时变刚度用多尺度函数的线性组合表示,从而将时变参数识别问题转化为时不变问题。将识别出的刚度和阻尼值作为初始条件,借助鱼群算法以截割头纵向振动的位移响应为目标函数对参数进行了优化。结果表明:参数优化后截割头纵向振动的位移响应的均值下降了18.3%。为验证优化结果的可靠性,利用ADAMS建立了整机的多刚体动力学模型。仿真结果表明,截割头的位移响应变化与理论计算的结果较接近,从而验证了优化结果的有效性。
截割头;虚拟激励法;小波;最小二乘法;鱼群算法
0 引言
截割头是纵轴式掘进机的工作机构,其作业环境恶劣,受煤岩赋存条件复杂、工作空间不断变化、工作载荷多变等因素影响,截割头在截割煤岩过程中会产生较大的振动,导致整机振动,这不仅容易损坏机器零部件、液压及电气元件,而且会降低机器工作可靠性和生产率。
通过现场调研和实验统计发现,纵轴式掘进机的振动形式有横向(机身宽度方向)、纵向(机身高度方向)和轴向(机身长度方向)三种,其中横向和纵向的振动较大,尤其是纵向振动最明显。
目前,掘进机振动特性的研究主要有试验法、频域分析法、载荷能量频率识别法、求解振动方程等方法。文献[1-3]均采用试验分析方法在井下实测了整机振动情况,得到了整机工作时的振动频率特征。童敏明等[4]使用远程监控系统,检测掘进机振动特性,并进行故障诊断和远程控制。张建广[5]通过建立人工岩壁和试验测试系统,并按照实际工况及不同工作参数对掘进机的振动数据从时域和频域进行了分析。本文第一作者等[6]采用小波包分析技术计算了重构后的功率谱,检测出振动较大的频率范围。
由于传统方法计算随机振动需求解复杂的频响函数,计算量大、耗时多、精度低,加之随机外载荷的反复作用导致系统的刚度和阻尼具有时变性,所以关于掘进机系统的参数识别及随机振动的研究目前还鲜见报道。本文利用Lagrange方法并结合虚拟激励法,建立纵轴式掘进机的纵向运动微分方程,将平稳随机响应转化为简谐响应进行计算,采用小波包函数多尺度逼近的方法,将系统的时变刚度和时变阻尼用小波尺度函数的线性组合近似,将时变参数的识别问题转化为由已知的正交尺度函数和系统的输入输出来估计线性组合中的时不变系数问题。
由于截割头纵向振动较大,故将识别出的结果作为参数优化的初始条件,采用鱼群算法,以截割头纵向振动的位移响应为目标函数对系统的参数进行优化。
1 小波参数识别原理
1.1多尺度小波包分析
设{Vj}j∈Z为尺度空间L2(R)的一个多分辨率分析[7],相应尺度函数为φ,小波函数为ψ,且满足尺度方程:
对于任意j∈Z,分解得
Vj-1=Vj⊕Wj
则尺度空间Vj与小波空间Wj的关系为
Vj-1=Vj+1⊕Wj+1⊕Wj=Vj+2⊕Wj+2Wj=…
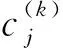
(1)
x(t)离散形式为
(2)
1.2时变参数识别方法
单自由度时变结构系统的运动方程[8]为

(3)
式中,m为质量;c(t)、k(t)分别为时变阻尼和时变刚度。
式(3)的离散形式为

(4)
将时变阻尼和时变刚度看作离散时间序列信号,设J层小波分解的小波系数和尺度系数已知,根据式(2)将其展开,对于慢变信号,能量大部分集中在低频部分,展开时可忽略第2项细节信号,仅由第1项概貌信号来近似表示:
(5)
将式(5)代入式(4)得
将离散时刻n=1,2,…,N的响应代入上式,有
g×q=r
g=[g(c)g(k)]T
q=[q(c)q(k)]T


由最小二乘法求出尺度系数和小波展开系数:
q=(gTg)-1gTr
将上式求出的结果代入式(5),可求出系统的时变刚度k(n)=q(k)和时变阻尼c(n)=q(c)。
2 掘进机动力学模型
2.1基本假设
纵轴式掘进机是结构复杂的大型工矿设备,为求解方便,将其进行适当的简化和假设[9]:根据组成将其简化为三自由度的动力学模型,截割头、悬臂和机体(包括行走机构)的质量分别为m1、m2、m3,煤壁单轴压缩强度恒定,各部分通过无质量的弹性元件连接,截割头与悬臂、悬臂与机体、机体与底板间的时变刚度和时变阻尼分别为k1(t)、k2(t)、k3(t)和c1(t)、c2(t)、c3(t),系统的刚度和阻尼不发生突变,随时间缓慢变化。由此建立纵轴式掘进机的纵向(垂直底板,y向)动力学模型,如图1所示。

图1 掘进机三自由纵向动力学模型
Lagrange方程为
(6)
式中,qj为系统广义坐标;Qj为广义坐标对应的广义力。
系统的势能V、动能T和耗散函数D为
(7)
将式(7)代入式(6),则掘进机纵向运动微分方程为
(8)
2.2随机激励作用下系统的运动微分方程
线性系统受到自功率谱密度为Sxx的平稳随机激励x(t)作用时,其响应的自功率谱Syy=|H|2Sxx。常规算法求系统响应需要大量时间求解频响函数矩阵H,计算较繁琐。
由虚拟激励法原理可知[10-11],当随机激励被简谐激励ei ω t代替时,相应的简谐响应y=Hei ω t,若在激励前乘以(Sx x)1/2,显然,响应谱为
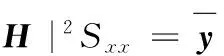
(9)
设线性系统受到随机平稳激励x(t)的作用,其运动方程为
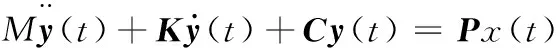
(10)
式中,x(t)为功率谱Sxx的平稳随机过程;P为给定常数向量;M为质量矩阵;K、C分别为刚度矩阵和阻尼矩阵。
统计分析表明[12],截割头载荷可视为平稳随机过程,截齿受力可按照瑞利分布的随机过程来考虑,截割头载荷是各截齿受力的叠加,其纵向随机激励自功率谱密度序列为
式中,Ry(n)为截断随机信号的自相关函数;ω=2πk/N。

(11)
P=[100]T
将刚度和阻尼作为未知量,把相同刚度和阻尼的系数移到同一边,则式(11)可改写为
(12)
根据上述的识别方法,将式(12)展开成矩阵形式:
G×H=R
(13)
对式(12)中待求的时变刚度k(t)、时变阻尼c(t),利用式(13)展开有
G=[G(c)G(k)]H=[H(c)H(k)]T
G(c)和G(k)矩阵关系式见表1。

表1 关系式系数
注:i=1,2,3;离散时刻n=1,2,…,N。
根据最小二乘法原理H=(GTG)-1R,识别出系统的时变阻尼和时变刚度分别为H(c)、H(k)。
2.3识别结果
以国产某型纵轴式掘进机为研究对象,其截割头、悬臂和机体的质量分别为m1=1051 kg,m2=2415 kg,m3=56 534 kg;采样频率fS=512 Hz,假设随机外载荷谱为服从瑞利分布的高斯白噪声谱。
当信号中存在噪声时,识别方程将发生病态,这里采用吉洪诺夫正则化方法来减小识别方程的不适定性对识别结果的影响,提高识别精度。
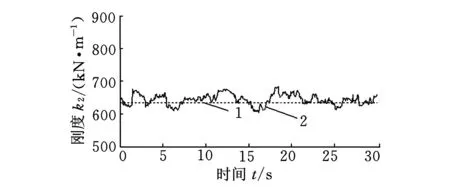
将变刚度和变阻尼分别用db4小波在尺度3上的正交尺度函数的线性组合表示,用最小二乘法识别的刚度和阻尼值如图2和图3所示。
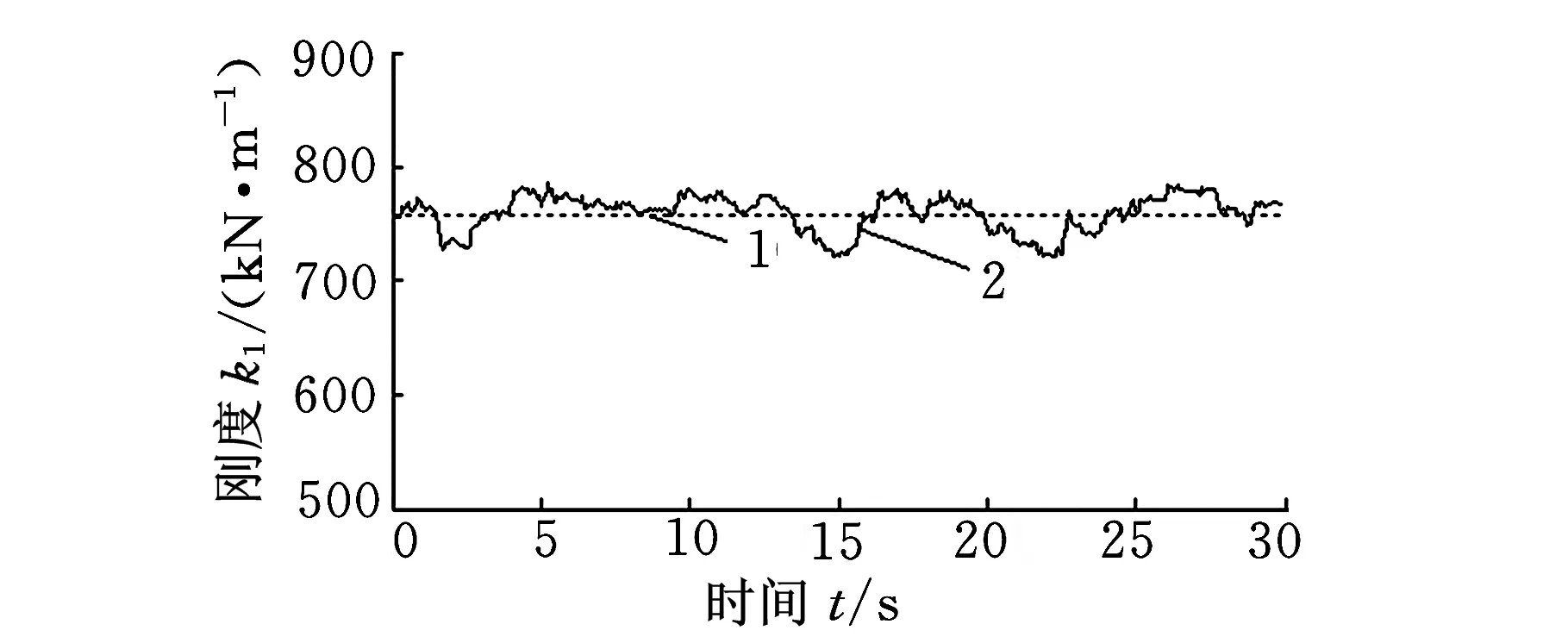
(a)截割头刚度k1
(b)悬臂刚度k2
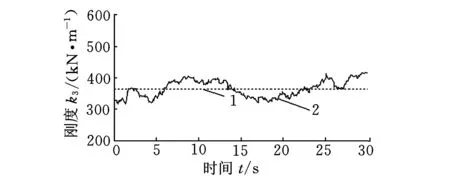
(c)机体刚度k31.理论值 2.5%噪声图2 刚度识别结果
由图2和图3可见,与理论值相比,在噪声的影响下,系统的刚度和阻尼的识别结果具有一定的波动性,由于系统的随机外载荷谱采用了假设条件,因此对计算精度会有一定影响,但其曲线始终在理论值的周围波动,且保持了较好的跟踪效果。在噪声影响下,相对于刚度识别结果,阻尼识别值与理论值之间的波动相对较大,刚度识别的效果好于阻尼,这是由于刚度值比阻尼值大很多,同时计算得出的相对误差阻尼要更大一些,可见,与刚度的识别结果相比,阻尼的识别对噪声较敏感,误差较大。

(a)截割头阻尼c1

(b)悬臂阻尼c2
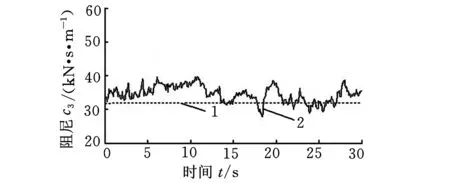
(c)机体阻尼c31.理论值 2.5%噪声图3 阻尼的识别结果
3 响应优化
3.1目标函数
以截割头纵向振动位移响应的均方值为目标函数,利用鱼群算法对系统的刚度和阻尼进行优化,以减小截割头的振动。令
(14)
将式(14)代入式(11),解得
利用系数矩阵的对称性,求得截割头、悬臂和机体的纵向位移响应:
式中,Λ*为Λ的伴随矩阵。
进而得到截割头(Syy1)、悬臂(Syy2)和机体(Syy3)的纵向位移响应功率谱矩阵:
Syy1=B1B1
Syy2=B2B2
Syy3=B3B3
当截割头受到纵向随机力Qy的作用时,其响应可由Duhamel积分表示为

式中,h(t)为脉冲函数。
其响应的相关函数为
Ryy(t1,t2)=E[y(t1)y(t2)]=
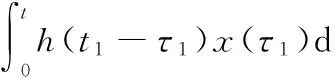

(15)
由维纳-辛钦定理有

(16)
h(t)与频率响应函数H(ω)构成傅里叶变换对:
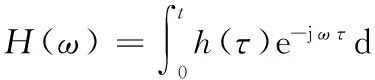
(17)
将式(16)、式(17)代入式(13),则响应的均方值为

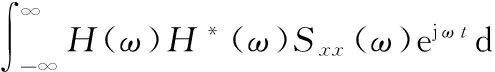
(18)
将式(9)代入式(18),截割头的纵向振动位移响应响应均方值可表示为

即目标函数为
(19)
3.2约束条件
将k1、k2、k3、c1、c2、c3作为优化变量,其取值范围如表2所示。

表2 优化变量取值范围
悬臂的最大挠度Ymax不应超过材料许用值[Y],即
Ymax=ql4/(8EI)≤[Y]
式中,q为集中载荷,N;E为材料的弹性模量,Pa;I为惯性矩,kg·m2;l为悬臂长度,m。
悬臂承受的最大剪应力τmax不应超过材料的极限应力[τ],即
τmax=T/Wn≤[τ]
式中,T为扭矩,N·m;Wn为抗扭截面系数。
3.3优化计算
借助MATLAB汇编语言编制鱼群算法程序,以式(19)为目标函数对参数进行优化。相关参数为:截割头转速nJ=46 r/min,截齿数z=48,煤岩崩落角Φ=45°,煤岩抗截强度A=378 N/mm,煤岩脆性度B=2.5,l=1.9 m,转矩Tm=580 N·m。取人工鱼群数50,感知距离1,最大迭代次数50,拥挤度因子0.618,移动步长0.1,觅食最大试探次数100。经优化,得到系统的刚度和阻尼参数值,见表3。优化前后的截割头位移响应如图4所示。

表3 优化结果
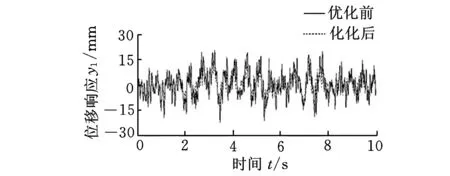
图4 截割头位移响应
由表3可见,k3和c3的变化量最大,这表明机体与底板间刚度和阻尼的增加可有效减小截割头的振动。通过对截割头位移响应的计算(图4)知,优化前后截割头的位移响应的均值分别为9.3 mm、7.6 mm,均值减小了18.3%。
4 结论的验证
4.1功率谱分析
由识别出的参数,计算得到在平稳随机激励作用下该机截割头、悬臂和机体的纵向位移功率谱密度仿真曲线,如图5所示。图5中的4个峰值集中在低频2~5 Hz,对应机体(2.8 Hz)、悬臂(3.4 Hz)以及截割头(4.2 Hz)的固有频率,这与文献[12-13]的结论及实验结果基本吻合,从而验证了识别结果的可靠性。

图5 位移功率谱密度
4.2模型仿真
根据多刚体动力学原理,利用Pro/E建立纵轴式掘进机三维模型,将掘进机整机模型映射到多体动力学软件ADAMS中,定义材料属性、载荷以及构件间的接触力、摩擦力和阻尼参数等,并对模型进行适当的简化,完成的整机模型如图6所示。

图6 掘进机多刚体动力学模型
根据建立的掘进机多刚体动力学模型,取步频300 Hz、仿真时间10 s,对识别参数值与优化后参数值分别进行仿真,求得截割头的纵向振动特征如图7所示。
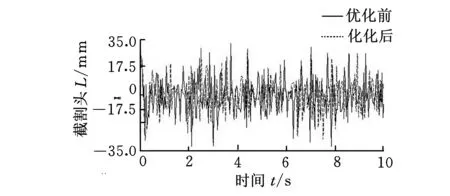
图7 模型仿真的截割头位移响应
统计表明,优化前后截割头的纵向位移响应均值分别为11.3 mm、9.8 mm,优化后均值减小了13.2%,模型仿真结果与理论计算结果相比,均值优化量仅相差5.1%,满足精度要求。
5 结论
(1)利用Lagrange方法并结合虚拟激励法,建立了纵轴式掘进机随机激励下的运动微分方程。
(2)根据Daubechies小波和最小二乘法原理,对系统的时变刚度和时变阻尼进行了识别,并以识别值为初始条件对参数进行了优化,优化后截割头振动的位移响应均值降低了18.3%,有效减小了截割头的振动。
(3)根据多刚体动力学原理,利用ADAMS建立掘进机的多刚体动力学模型,模型仿真结果与理论计算值较接近,验证了优化结果的可靠性。
[1]Kröger G,Brzchta P.Neue Meβund Diagnose System für Fördererund Fobelanlagen[J].Glückauf,1991,127(17/18):778-785.
[2]黄民,吴淼,安伟,等.横切割头掘进机械振动特性研究[J].机械工程学报,2002,38(8):89-93.
Huang Min,Wu Miao,An Wei,et al.Research on Vibration Characteristics of Horizontal Axis Tunneller[J].Chinese Journal of Mechanical Engineering,2002,38(8):89-93.
[3]Tao Alvarez J,Menendez M.Rodriguez Diez R,et al.Experimental Results of a Low-power Roadheader Driving a Gallery with Different Types of Rock at the Face[J].Tunnelling and Underground Space Technology,2003,18(4):395-404.
[4]童敏明,吴轲.基于振动传感器的掘进机故障监测系统[J].煤矿机械,2010,31(5):241-243.
Tong Minming,Wu Ke.Based on Vibration Sensor Tunnel Boring Machine Fault Monitoring System[J].Coal Mine Machinery,2010,31(5):241-243.
[5]张建广.纵轴式掘进机截割人工岩壁的振动试验研究[J].煤炭科学技术,2011,39(8):76-78.
Zhang Jianguang.Study on Vibration Experiment of Artificial Rock Wall Cutting with Longitudinal Shaft Type Mine Roadheader[J].Coal Science and Technology,2011,39(8):76-78.
[6]李晓豁,韩宇飞.掘进机截割载荷极值能量的频率识别[J].煤炭学报,2008,33(4):459-461.
Li Xiaohuo,Han Yufei.Frequency Recognition of Cutting Loads Extreme Energy for Roadheader[J]. Journal of China Coal Society, 2008,33(4):459-461.
[7]潘学萍,袁姗姗,鞠萍,等.负荷随机扰动下的电力系统小波模态参数识别[J].电力自动化设备,2012, 32(4):6-10.
Pan Xueping, Yuan Shanshan, Ju Ping, et al. Wavelet Based Electromechanical Mode Shape Identification From Ambiet Data of Random Load Excitayion[J]. Electric Power Automation Equipment,2012,32(4):6-10.
[8]潘学萍,扈卫卫,尚霏.多信号模态参数识别的小波方法[J].电力自动化设备,2013,33(5):31-36.
Pan Xueping,Hu Weiwei,Shang Fei.Criterion of Current Differential Protection Based on Amplitude and Phase Difference of Fault Current[J].Electric Power Automation Equipment,2013,33(5):31-36.
[9]居乃鵕.装甲车辆动力学分析与仿真[M].北京:国防工业出版社,2002.
[10]李杰,秦玉英,赵旗.汽车行驶平顺性建模与仿真的新方法[J]. 中国机械工程,2009,20(13):1264-1269.
Li Jie,Qin Yuying,Zhao Qi.A New Mathematical Modelling and Simulation Method for Vehicle Ride Comfort[J].China Mechanical Engineering,2009,20(13):1264-1269.
[11]李晓豁.掘进机截割头随机载荷的模拟研究[J].煤炭学报,2000,25(5):73-76.
Li Xiaohuo.Simulation Study of Random Loads on a Cutting Head of Roadheader[J].Journal of China Coal Society,2000,25(5):73-76.
[12]李晓豁.掘进机截割头的关键技术研究[M].北京:机械工业出版社,2008.
[13]李晓豁,韩宇飞.纵轴式掘进机截割的功率谱分析[J].中国工程机械学报,2007,5(2):134-137.
Li Xiaohuo,Han Yufei.Spectral Analysis of Cutting Power for Longitudinal Excavators[J].Chinese Journal of Construction Machinery,2007,5(2):134-137.
(编辑袁兴玲)
Vertical Random Vibration Response and Optimization of Cutting Head Based on Parameter Identification
Li XiaohuoHe YangJiao LiSha YongdongLi Ting
Liaoning Technical University,Fuxin,Liaoning,123000
In order to reduce the vibration of a longitudinal roadheader’s cutting head,differential equations of motion of the roadheader were derived by using Lagrange equation and pseudo-excitation method.By expanding the time-varying stiffness and damping of the system into linear combination of a series scaling functions based on Daubechies wavelet’s compactness and regularization and least-square method,the time-varying parameter identification problem was turned into the problem of identifying invariant parameters.Taking the identifying parameters as the initial conditions,choosing displacement response of the cutting head as an optimal objective and parameters were optimized by means of fish-swarm algorithm.The results show that the displacement response of the cutting head is decreased by 18.3% after optimized.A multi-body dynamic model of the roadheader was simulated in ADAMS for the sake of identifying the conclusion,the model simulation results and the theoretical value are relatively close,which implies validity of the optimized conclusion.
cutting head;pseudo-excitation method;wavelet;least-square method;fish-swarm algorithm
2013-07-30
2014-12-09
国家自然科学基金资助项目(59774033);中国煤炭工业协会科学技术研究指导性计划资助项目(MTKJ2011-325);辽宁省大型工矿装备重点实验室资助项目(2008403010)
TD421.5DOI:10.3969/j.issn.1004-132X.2015.06.021
李晓豁,男,1953年生。辽宁工程技术大学机械工程学院教授、博士研究生导师。主要研究方向为现代机械设计理论与方法、机电液系统仿真与应用。出版专著3部,发表论文396篇。何洋,男,1982年生。辽宁工程技术大学机械工程学院博士研究生。焦丽,女,1979年生。辽宁工程技术大学机械工程学院讲师、博士。沙永东,男,1980年生。辽宁工程技术大学机械工程学院讲师、博士。李婷,女,1984年生。辽宁工程技术大学机械工程学院博士研究生。
