基于主断面刚度优化分配的车身正向概念设计

刘子建　周小龙　田海豹　吕　程

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

基于主断面刚度优化分配的车身正向概念设计

刘子建周小龙田海豹吕程

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

提出了基于刚度优化分配的车身正向概念设计流程。根据车身结构拓扑与刚度分布紧密关联和相互影响的特点，提出了车身刚度链设计方法。建立了基于梁单元的车身简化模型，确定了18个主断面位置,建立了以主断面为节点的车身刚度链数学模型。针对车身刚度分布问题，研究了基于车身刚度链的整体刚度优化分布方法，建立了车身弯曲刚度优化分布问题的数学模型，利用遗传算法进行了求解，确定了各主断面的材料分布。与已有近似标杆车CAE模型的刚度仿真结果进行对比,验证了该刚度优化分布方案的合理性以及车身刚度链方法的有效性。

车身概念设计;简化模型;车身刚度链;刚度优化分配

0　引言

概念设计是车身结构设计的前期阶段，任务是为详细设计提供可行方案。概念设计占据了车身开发周期约70%的时间,车身的基本结构及主要性能都取决于概念设计的结果。车身概念设计的特点一方面是既要适于外观造型和整车布置等设计创新,又要满足安全、NVH、轻量化和工艺等性能的需求,一旦留下设计缺陷,在后续的流程中将难以弥补;另一方面,由于概念设计的信息不确定程度高,导致设计修改频繁、效率低、周期长。因此研究易于修改和计算的车身概念设计模型和设计方法至关重要[1]。

轿车车身大多数采用全承载式结构，衡量其承载能力的基本指标是车身刚度。车身刚度设计是概念设计阶段必须重点关注和解决的关键技术问题，国内外整车企业都非常重视。福特和沃尔沃公司研究人员讨论了轿车刚度设计与NVH、拓扑优化的关系[2-3]；迟瑞丰等[4]建立了概念设计阶段车身结构的几何模型及有限元模型,进行了静刚度分析;邢子敬等[5]研究了概念设计中梁截面对车身刚度的影响。

本文提出车身刚度链设计方法，以车身主断面刚度优化分配为目标，建立易于修改和快速计算的车身概念设计模型，探讨实现车身正向概念设计、提高设计质量、缩短研发周期的新设计方法。

1　轿车车身正向概念设计流程

目前普遍采用的基于标杆车型的车身逆向概念设计流程如图1所示。车身逆向概念设计的大部分数据来源于标杆车，原车型的束缚会限制车身造型和布置等创新的空间，将对标测试验证后的刚度计算模型用于新车型，不仅依赖于设计者CAE的经验，较多的补充实验和验证也是必不可少的。正向设计的方法更适合车身概念设计，从产品的规划与定义开始设计，由需求确定性能,再由性能确定结构,最后对结构进行分析、验证。正向设计的优点是使车身概念设计能够充分满足车型创新设计的需求,设计过程更为严谨和高效。鉴于此，本文提出了基于刚度优化分配的车身正向概念设计流程,如图2所示。

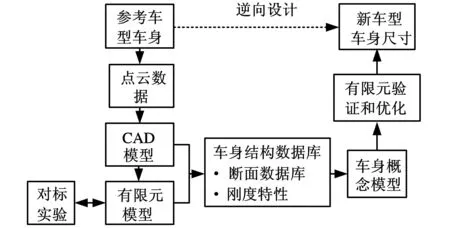
图1　车身逆向概念设计

图2　车身正向概念设计

2　车身简化几何模型建模

车身正向概念设计有两个重要背景:一是设计对象复杂而数据不完备，除了整车性能参数指标可作为确定的输入条件外，其他信息的不确定程度都很高；二是概念设计阶段常常需要分析多个有较大差异的技术方案，直接采用结构详细的车身模型难以快速进行方案修改[6]。从车身简化几何模型出发讨论刚度分配方法，可以抓住主要矛盾，更好地适应概念设计的需求。为此提出如下假设:①先考虑车身主要承载梁结构，暂不考虑地板、顶盖等覆盖件;②梁之间为刚性接头，暂时不考虑焊点特性;③曲梁用多段直梁近似逼近。

本文建立车身简化几何模型的原始依据是造型设计确定的某轿车车身的A级曲面，如图3所示。

图3　某车型的车身A面　图4　初始框架结构

首先以车身A面为载体,考虑承载构件,得到车身的初始框架结构,如图4所示。

然后基于初始框架结构,遵循特征点采集原则[7],采集得到车身上的特征点,如图5所示。采集车身特征点时,不可避免地会出现误差较大的点，即噪声点,故不能将这些点直接用于构建车身简化几何模型，需对点云数据进行预处理，校正噪声点并减少冗余数据，保留有效信息。对采集的特征点进行预处理的方法如下[8]：①在全局坐标系中记录每个特征点的坐标数据；②依据车身形状有序采集数据、特征点的拓扑关系;③为方便后期数据处理，将某些数据进行坐标变换；④剔除异常点,对数据进行除噪、滤波和精简,增强数据的有效性和合理性;⑤提取控制几何形状特征点，用于后续建模区域划分。

图5　车身特征点

按照上述方法构造出每根梁结构的曲线段,拼接成车身线框模型，进一步检查曲线段的连接关系是否正确和足够光顺等，整理后的车身简化线框模型如图6所示。在图6的基础上确定主断面的位置,得到二分之一车身的18个主断面位置，如图7所示,主断面编号及具体位置见表1。

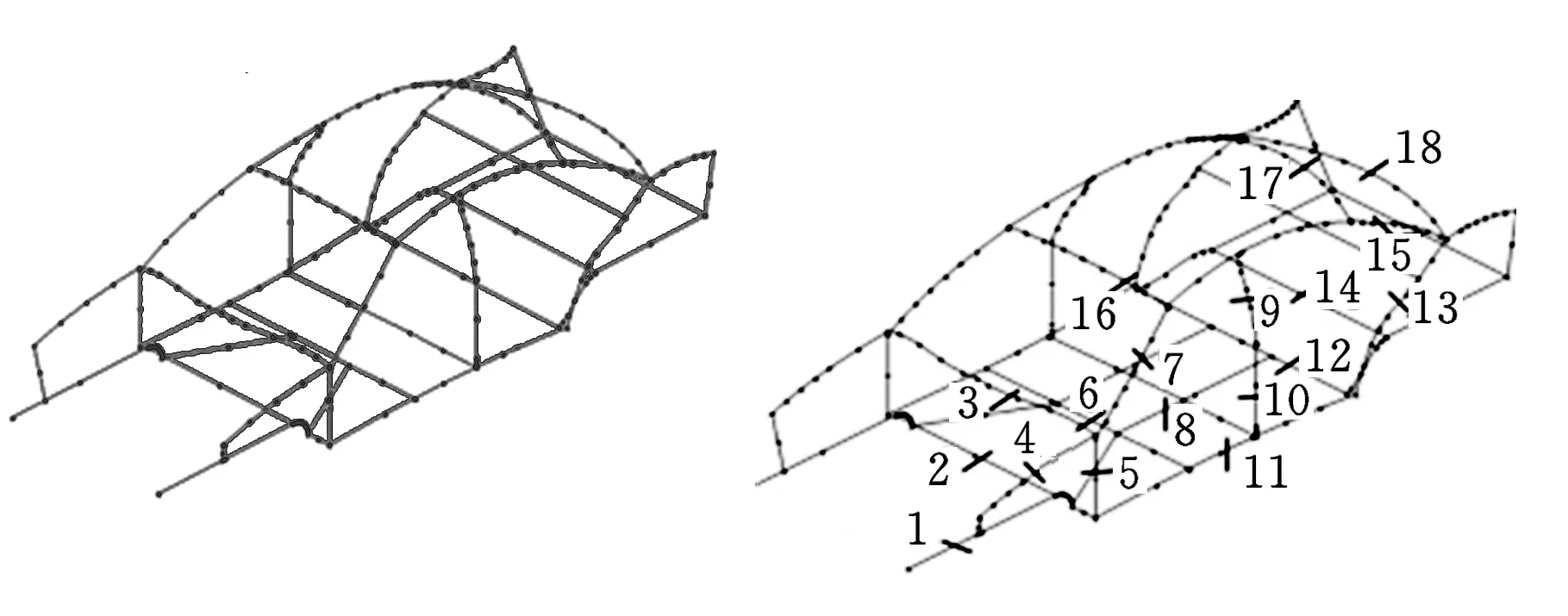
图6　车身简化线框模型　图7　车身主断面的分布

3　基于车身刚度链的刚度优化分配

本文提出的车身刚度链是以车身简化几何模型表示车身结构拓扑关系，以结构力学、梁单元法和传递矩阵法建立车身整体刚度与局部刚度之间关系，适用于车身正向概念设计的一种车身结构分析和计算模型。由于刚度链可以用解析法求解，因而可以快速完成车身刚度的分析和优化分配，并由刚度的优化分布结果确定车身材料的优化分布方案,进而结合工艺等需求完成车身主断面的设计，因而基于刚度链的车身刚度优化分配设计也是一种能够充分满足车身创新设计需求,适用于概念设计阶段频繁修改需求的新型设计方法,其流程如图8所示。

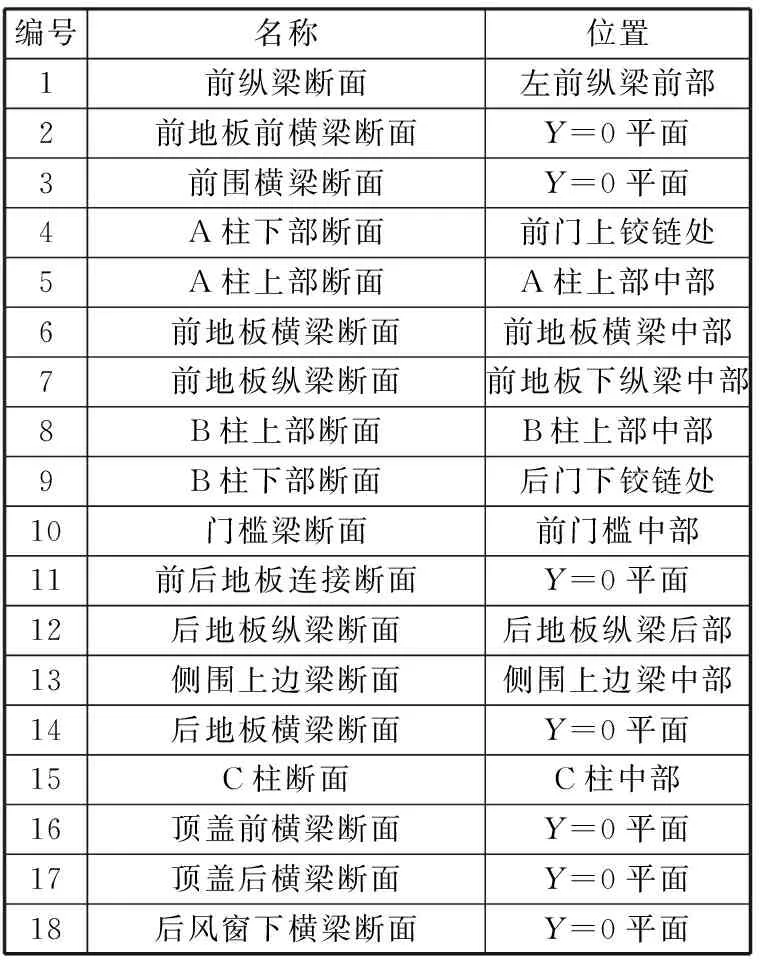
表1　车身主断面位置描述

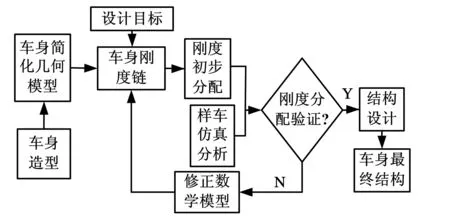
图8　基于刚度链的车身刚度优化分配流程

3.1基于传递矩阵法的车身刚度链建模

传递矩阵法[9-11]的基本思想是把一个整体结构的力学分析问题转化为若干单元或子系统的“对接”与“传递”的力学分析问题。本文将传递矩阵法的理论和方法应用到车身结构分析中，推导出车身刚度链数学模型。用传递矩阵法推导刚度链需进行以下假定:①构件符合小变形、小应变假定；②材料为各向同性的线弹性材料;③载荷作用在刚度链的节点上。

基于以上描述,车身刚度链以主断面、接头、搭界面、主焊点为节点,以载荷和变形在相关梁单元之间的传递路径为链,描述结构与材料、载荷与变形以及节点与节点之间的相互作用关系。车身刚度链可视为由多个子刚度链耦合而成，按照化繁为简的原则从整体到局部逐级分解，得到若干个形式相对简单的子刚度链,然后分别建立每个子刚度链的计算模型,再向上逐层组合迭加,最终建立车身的完整刚度链模型，如图9所示。

图9　整体刚度链的构成关系

轿车车身弯曲刚度是评价车身性能的一个重要指标。车身弯曲工况如图10所示,车身后悬位置处约束X、Y、Z方向的平动自由度，车身前悬架位置处约束Y、Z方向的平动自由度,在座椅安装点左右对称施加垂直向下的力F,F=1 kN,车身整体的弯曲刚度可由车身底架处最大垂直挠度来评价。

图10　车身弯曲工况

根据对称性将车身分解为左侧围系统、右侧围系统和9个横梁,如图11所示。左右侧围系统可再分解成A柱上部、A柱下部、B柱上部、B柱下部、C柱、侧围上边梁、前纵梁、门槛梁和后地板纵梁共9种形式的梁。下面以车身侧围为例讨论车身刚度链建模方法。

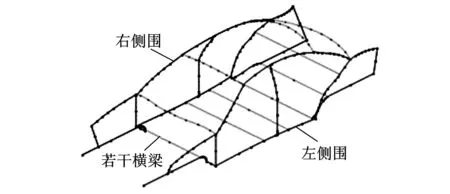
图11　车身刚度链的分解

图12所示为车身左侧围的受力及单元划分情况,图中数字为节点编号，带圈数字为单元编号。根据简化几何结构的拓扑关系、主断面分布、载荷位置等将车身侧围梁结构划分成17个单元、15个节点。如单元①为前纵梁,对应截面编号1;单元②、③、④组成门槛梁,对应截面编号10;单元⑤、⑥、⑦组成后地板纵梁,对应截面编号12;单元⑧为A柱下部,对应截面编号4;单元⑨为A柱上部,对应截面编号5;单元⑩、、、、组成侧围上边梁,对应截面编号13;单元为C柱,对应截面编号15;单元为B柱上部,对应截面编号8;单元为B柱下部,对应截面编号9。进一步将上述17个单元分成9个截面属性集合,记为{C}(i),其中{C}(i)={A,Iy,Iz},i为截面编号,取值为1、4、5、8、9、10、12、13、15，且与表1截面编号一致,A为主断面面积,Iy、Iz为主断面惯性矩。

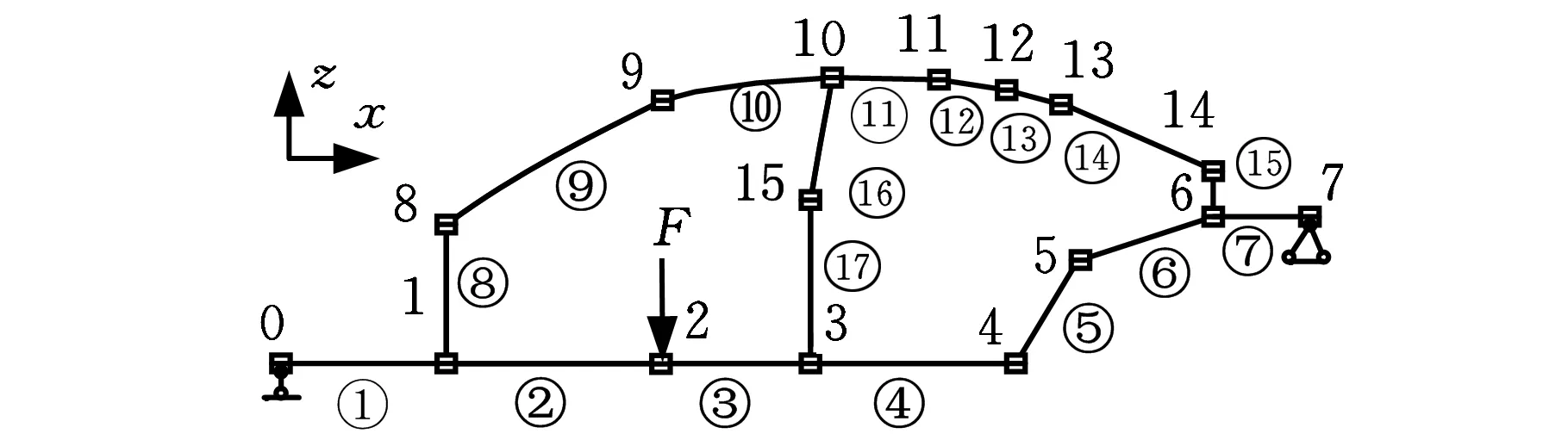
图12　车身侧围力学模型及单元划分

按照拓扑关系,车身侧围刚度链在耦合点1、3、6、10处被拆分为3个子刚度链,分别为0-1-2-3-4-5-6-7,1-8-9-10-11-12-13-14和3-15-10,记为子刚度链1、子刚度链2、子刚度链3，如图13所示。

(a)子刚度链1

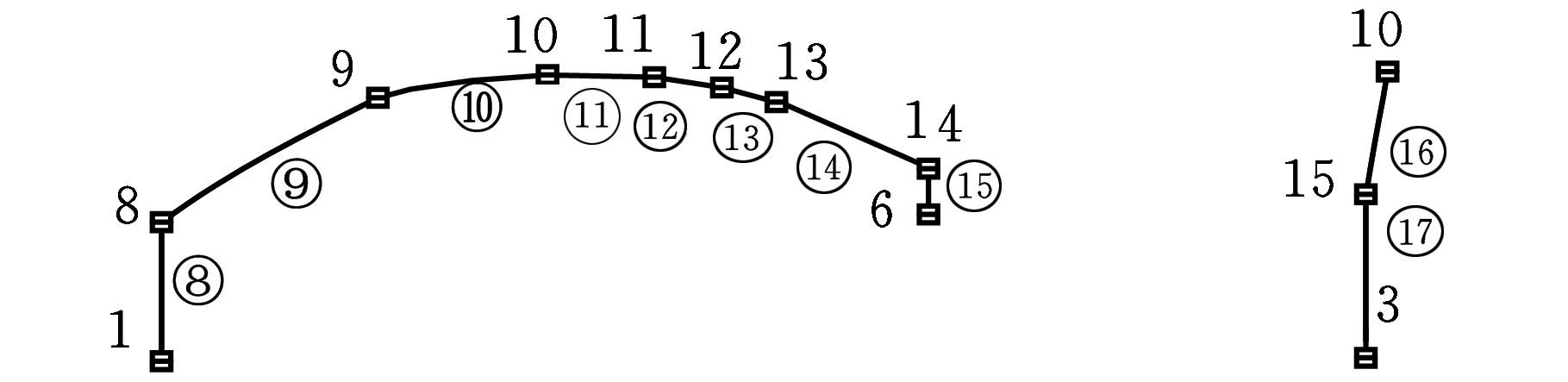
(b)子刚度链2(c)子刚度链3图13　车身侧围刚度链的拆解

下面以子刚度链1为例讨论建模方法。如图13a所示,节点0和节点7处为铰接约束,在节点2处有垂直向下集中载荷F。节点1、节点6为耦合点,引入耦合点未知状态向量。故可列出节点1和节点7的状态向量:

(1)

(2)

节点1～节点6的载荷向量为

(3)

(4)

(5)

(6)

(7)

式中,Sl(i)、Sr(i)分别为单元i左右端节点状态向量;Ql、Qr分别为铰支承处的径向约束反力;φl、φr分别为节点1和节点7处平面内转角;R(i)为节点i处的载荷向量;qx(i)、qz(i)、My(i)分别为节点i处轴向集中力、径向集中力和集中力偶。

根据传递矩阵法推导公式，可列出子刚度链1的传递方程

(8)

其中，T(i)为单元i的场矩阵,除单元5和单元6外,其他单元的局部坐标系方向均与全局坐标系相同,场矩阵的表达式为

i≠5,6

(9)

式中,l(i)为单元i的长度;A(i)为单元i的截面面积;I(i)为单元i的截面惯性矩；E为弹性模量；G为剪切模量；μ为泊松比。

由于单元5、单元6的局部坐标系与全局坐标系有夹角,需进行坐标变换来求出场矩阵。由节点坐标变换可知,单元k的场矩阵从局部坐标系变换到全局坐标系的变换公式为

(10)

单元5的场矩阵为

(11)

(12)

其中,α(5)为单元5的局部坐标系与全局坐标系的夹角,同理可得到T(6)。

车身弯曲刚度用加载点处的力和位移表征,故需建立节点2与刚度链的关系，设节点2竖直向下的变形量Δz为基本未知向量,由式(8)可以得出链0-1-2-3-4-5-6-7的刚度链数学表达式，记为

f1({C}(1),{C}(10),{C}(12),Δz)=0

(13)

同理可得出子刚度链2和子刚度链3的链数学模型。

子刚度链1与子刚度链2在节点1和节点6处耦合,耦合点状态向量集合记为{Q}(1,2),建立两者的耦合方程：

(14)

同理,子刚度链1与子刚度链3在节点3处耦合,耦合点状态向量集合记为{Q}(1,3);子刚度链2与子刚度链3在节点10处耦合，耦合点状态向量集合记为{Q}(2,3)。将上述三个子刚度链数学模型记为f1、f2、f3,耦合方程记为g(1,2)(f1,f2,{Q}(1,2)),g(1,3)(f1,f3,{Q}(1,3)),g(2,3)(f2,f3,{Q}(2,3)),联立方程组有

(15)

式(15)为车身侧围刚度链,可简单记为F1。同理可得出另一个车身侧围和9个横梁的刚度链,分别记为F2,F3,…,F11。把这些子系统按照耦合点和拓扑关系组合起来,子系统刚度链i与子系统刚度链j的耦合方程记为G(i,j),则车身整体刚度链模型为

(16)

根据式(15)可以求得节点2竖直向下的变形量Δz与各主断面{C}(i)的函数关系式：

Δz=f({C}(1),{C}(2),…,{C}(18))

(17)

3.2侧围刚度优化分配

在概念设计阶段如果直接参考标杆车如图14所示的主断面结构确定材料的分布，从而完成刚度的分配，将遇到主断面形状复杂、参数多、计算耗时的困难。本文先采用如图15所示简化了形状的薄壁矩形截面求解各主断面材料分布规律，再考虑工艺等需求确定主断面最后形状，实现车身刚度分布的快速计算和优化。

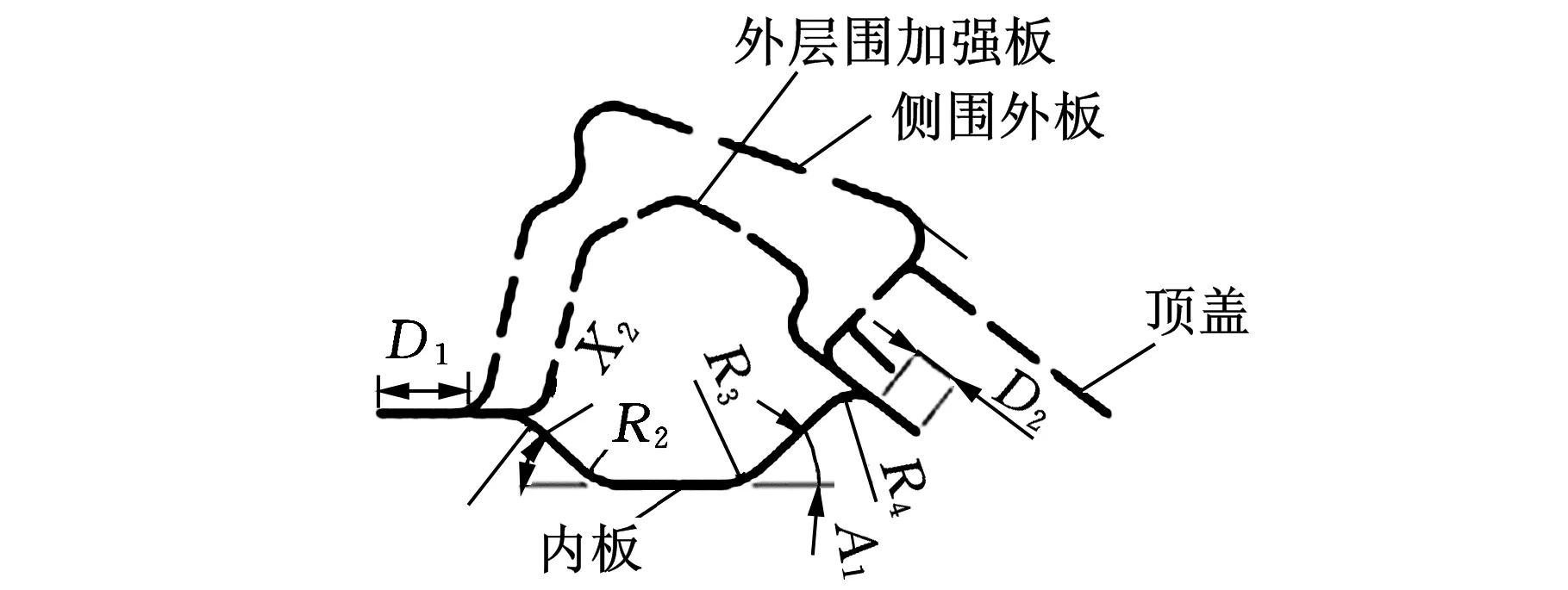
图14　标杆车主断面结构

图15　薄壁矩形截面

基于车身刚度链的刚度优化分布方法是以车身刚度链为载体，以车身载荷传递与材料分布最佳匹配为目标，通过遗传算法，将车身材料合理地分布到刚度链节点上的方法。为了定量表示主断面刚度分布情况，定义截面面积S与车身整体刚度EI的比值为该主断面的当量刚度，用EIe表示(量纲一),公式为

(18)

3.2.1刚度优化分布数学模型

现选取设计变量为侧围9个主断面简化截面的结构参数：

X=(X1,X4,…,X15)

(19)

Xi=(hi,wi,ti)

(20)

其中,hi、wi、ti分别为第i个主断面简化截面结构参数。为了减少设计变量,取板厚ti=0.8 mm,所以共有18个优化设计变量。考虑到概念设计阶段设计自由度大,因此截面初始尺寸及变化范围设定如下。门槛梁：h=w=300 mm[250,350],t=0.8 mm。其余梁:h=w=100 mm[20,200],t=0.8 mm。

考虑如图10所示的车身弯曲刚度工况,约束条件为加载点的位移Δz小于1 mm,表达式如下：

加载点位移即刚度约束为

Δz=f({C}(1),{C}(4),…,{C}(15))≤1 mm

(21)

车身整体刚度表达式为

(22)

综合考虑性能指标和经济指标,在满足车身弯曲刚度的条件下应使车身质量最小,因此将车身质量作为目标函数,表达如下：

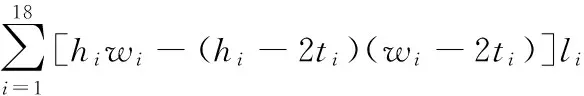
(23)

式中,li为第i个梁结构的长度,li为已知量,可根据车身简化几何模型得到;ρ为已知的材料密度。

3.2.2优化求解及结果分析

图16　目标函数收敛情况

选用遗传算法[13]能有效地求解出模型全局最优解或近似最优解。在MATLAB中进行优化计算,目标函数的收敛情况如图16所示。在满足弯曲刚度工况下,车身最小质量为0.1326 t。

优化后得到的主断面截面参数如表2所示,主断面编号与表1中的编号相同。

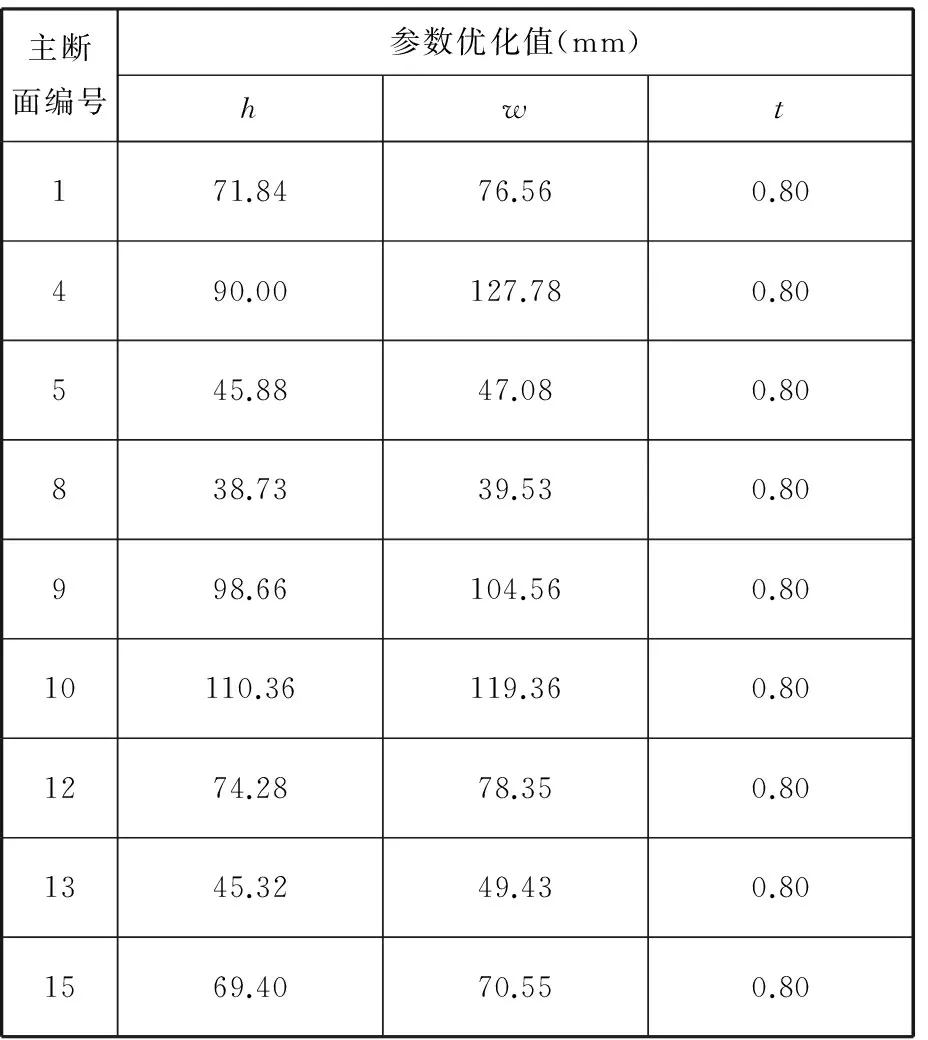
表2　优化后的侧围主断面截面参数

将上述优化结果代入计算式(21)、式(22),计算结果为

Δz=f({C}(1)，({C}(2)，…,{C}(15))=0.4683 mm

(24)

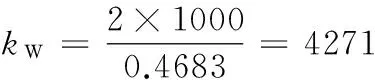
(25)

利用主断面截面参数就可计算出其面积S,惯性矩Iy、Iz以及当量刚度。得出的当量刚度如图17所示(侧围仅涉及编号为1、4、5、8、9、10、12、13、15的主断面)。

图17　车身侧围弯曲刚度在主断面上的分布情况

从图17中可以清楚看到,编号为1、4、9、10的主断面分布的当量刚度较大,其中以门槛梁断面的影响程度最大,结果与文献[13-14]研究的结论相同。

为验证上述车身弯曲刚度优化分布结果的正确性,本文分析了标杆车的弯曲刚度分布情况，再与前者进行对比。将标杆车在HyperWorks软件中进行有限元分析，在保证充分反映实际结构力学性能的前提下对车身部件作了必要简化,本文建立的有限元模型包括461 942个单元、465 722个节点、17 925个焊点,如图18所示。

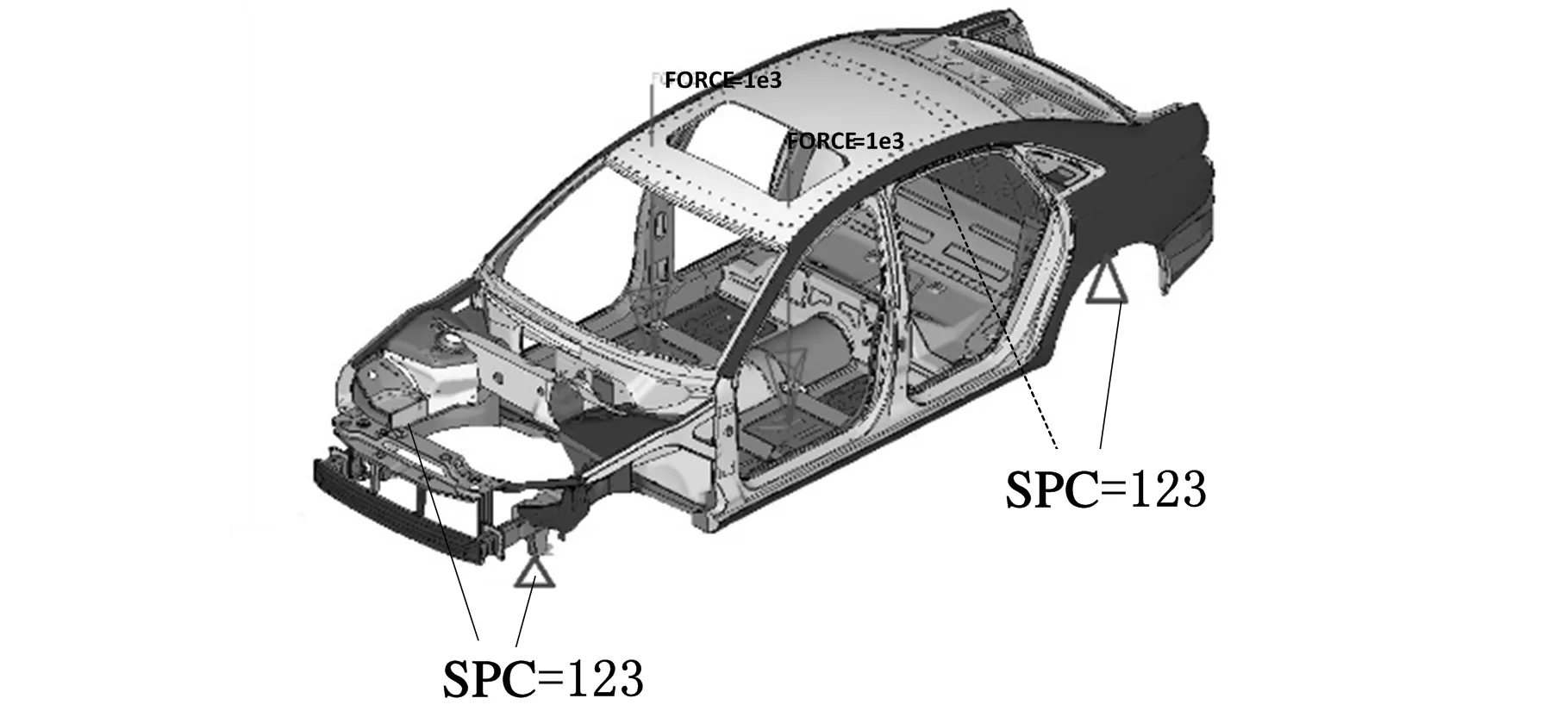
图18　计算车身弯曲刚度的有限元模型

经过计算,结果可在HyperView中查看。左右加载点位移分别为0.614 mm和0.613 mm。代入弯曲刚度计算式(22),得到的结果为

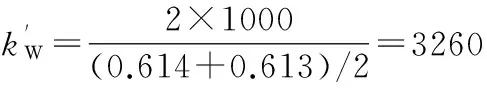
(26)

将基于车身刚度链的刚度优化结果与标杆车的刚度优化结果进行对比分析,结果如图19所示。

图19　刚度链计算结果与标杆车对应数据对比

从图19中可以看出,标杆车主断面当量刚度的变化幅度比较大,如最大当量刚度值与次大当量刚度值相差0.106,而刚度链优化结果差别为0.019,约为前者的1/5,这说明本文优化的刚度分布比较均匀、合理,整体刚度(4271 N/mm)也比标杆车(3620 N/mm)大。因为基于车身刚度链的刚度优化分布不仅考虑了整体刚度与局部刚度之间的关系，还考虑了局部刚度与局部刚度之间的关系，从而保证了整体刚度能够最优地分布到各个刚度链节点上。所以基于车身刚度链的刚度优化分布方案通过对整体刚度进行正向设计，保证了整体刚度性能最优且车身质量最小。与基于标杆车和CAE技术的车身概念设计方法相比，车身刚度链概念设计方法采用解析方法求解，计算效率大幅提高。

4　结论

(1)针对现有车身逆向概念设计存在设计效率低、准确度不高等问题，提出了基于刚度优化分配的车身正向概念设计流程，此流程更适用于车身自主开发。

(2)根据车身结构拓扑与刚度分布紧密关联和相互影响的特点，提出了车身刚度链设计方法，以某款车身的A级曲面为出发点，建立了基于线框的车身简化模型，确定了18个主断面位置,建立了以主断面为节点的车身刚度链。

(3)针对车身刚度分布问题，研究了基于车身刚度链的整体刚度优化分布方法，建立了车身侧围弯曲刚度优化分布问题的数学模型，用遗传算法进行了求解，并通过对比已有近似标杆车刚度参数，验证了刚度优化分布方案的合理性以及本文研究方法的可行性，而计算效率大为提高。

(4)本文对车身概念设计几何模型进行了一些简化，并对侧围的弯曲刚度优化分布进行了研究。应进一步考虑弯曲刚度、扭转刚度，在满足所有工况下进行车身刚度优化，最终确定整车刚度优化分布，即获得最佳的材料分布。最后综合考虑车身NVH、安全、疲劳、工艺等多学科问题，完成车身主断面的结构设计,是值得深入研究的问题。

[1]Lan Fengchong,Chen Jiqing,Lin Jianguo.Research on Parameterized Modeling and Application for Car[J].Computer Integrated Manufacturing System,2005,2(11):19-20．

[2]Ford Motor Company.Guidelines for Modeling an Automobile Body for NVH Analysis-Simplified Models[R].California:The University of California,1995.

[3]Torstenfelt B,Klurbring A.Conceptual Optimal Design of Modular Car Product Families Using Simultaneous Size and Topology Optimization[J].Finite Elements in Analysis and Design,2007,43:1050-1061.

[4]迟瑞丰,胡平,侯文彬,等.概念设计阶段的车身结构分析[J].汽车工程,2010,32(3):209-212．

Chi Ruifeng,Hu Ping,Hou Wenbin,et al.Body Structure Analysis of the Conceptual Design Stage[J].Automotive Engineering,2010,32(3):209-212.

[5]邢子敬,侯文彬,刘斌,等.概念设计中梁截面对车身刚度影响的研究[J].汽车技术,2009(10):21-24.

Xing Zijing,Hou Wenbin,Liu Bin,et al.Conceptual Stiffness Design of the Beam Cross-section of the Body Research[J].Automotive Technology,2009(10):21-24.

[6]任建英.概念设计阶段轿车白车身结构定性仿真模型的建立研究[D].上海:上海交通大学,2009.

[7]张志亮.逆向工程开发技术及其在福田重卡车身开发中应用[D].大连:大连理工大学,2003.

[8]张欣宇.基于逆向工程的汽车外形设计方法的应用研究[D].武汉:武汉理工大学,2008.

[9]刘庆潭,倪国荣.结构分析中的传递矩阵法[M].北京:中国铁道出版社,1997.

[10]李青宁.变截面杆元传递矩阵法[J].西安建筑科技大学学报(自然科学版),2001,23(1):18-23.

Li Qingning.Variable Cross Bar Element Transfer Matrix Method[J].Xi’an University of Architecture & Technology(Natural Science),2001,23(1):18-23.

[11]王世忠.结构力学与有限元法[M].哈尔滨:哈尔滨工业大学出版社,2003.

[12]王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002.

[13]张平.车身结构主断面对车身静刚度影响的研究[D].上海:同济大学,2006.

[14]姚乾华,陈昌明.基于车身主断面力学特性的灵敏度分析[J].车辆与动力技术,2007(4):36-38,42.

Yao Qianhua,Chen Changming.Main Body Section Based on the Sensitivity Analysis of the Mechanical Properties of the Vehicle and Power Technology,2007(4):36-38,42.

(编辑袁兴玲)

Forward Conceptual Design of Car Body Using Stiffness Optimal Allocation of Main Sections

Liu ZijianZhou XiaolongTian HaibaoLü Cheng

Hunan University, State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Changsha,410082

A top-down conceptual design process was proposed based on the stiffness optimum distribution in car-body conceptual design phase.According to the features that the car-body structural topology was closely related to and mutually influences with stiffness distribution,a method of car-body stiffness chain was proposed.A simplified car-body wireframe model was established，18 main sections were defined and the mathematic model of car-body stiffness chain with main sections as nodes was built.Stiffness optimum distribution was studied based on car-body stiffness chain and the mathematic model of car-bodybending stiffness optimum distribution was built and then solved by genetic algorithm to obtain the material distribution in each main section.The rationality of stiffness optimum distribution and the availability of car-body stiffness chain were verified by comparing with the CAE analyses of approximate benchmarking car.

conceptual design of car body;simplified model;car-body stiffness chain;stiffness optimum distribution

2013-08-20

2014-12-04

国家重点基础研究发展计划(973计划)资助项目(2010CB328002);国家自然科学基金资助项目(51475152)

U463.82DOI：10.3969/j.issn.1004-132X.2015.06.025

刘子建,男,1953年生。湖南大学机械与运载工程学院博士研究生导师。主要研究方向为机械设计及理论。出版专著1部,发表论文10余篇。周小龙,男,1989年生。湖南大学机械与运载工程学院硕士研究生。田海豹,男,1988年生。湖南大学机械与运载工程学院硕士研究生。吕程,女,1988年生。湖南大学机械与运载工程学院博士研究生。