基于公理设计的机械系统稳健性分析及应用

程贤福　李　骏　徐尤南　朱启航

华东交通大学,南昌,330013

基于公理设计的机械系统稳健性分析及应用

程贤福李骏徐尤南朱启航

华东交通大学,南昌,330013

以用户需求为切入点，对产品的功能语义和功能需求进行元模型描述,将用户需求转化为功能要求。以公理设计为指导框架，基于独立公理和Z字形映射方式,寻找并确定设计参数，明确功能要求之间及其与设计参数的相互关系，建立完整设计矩阵。将公理设计矩阵转换为设计结构矩阵并对其进行重构，生成几个相互之间具有较小依赖度的聚类耦合模块，得到系统稳健关联矩阵。然后将各个模块之间的关联参数作为可控因素，通过试验设计分析其对目标影响的重要程度并实施针对性的控制与调整，从而提升机械产品系统的稳健性。基于所提出的稳健性分析方法进行了起重机小车的设计，说明了该方法的应用过程,证明该方法是可行性的。

稳健性分析；试验设计；公理设计；机械系统

0　引言

在产品设计的早期阶段,设计效率的提高对缩短开发时间、降低成本至关重要;提高产品系统设计的稳健性,可以减少整个产品生命周期中的失误,从而大大地提高设计质量[1]。系统设计阶段的设计决策对整个产品开发过程有着非常重要的影响，为使产品设计具有可适应性以满足用户的多样化需求，应提前对相关设计活动和组织计划进行合理规划。此外,设计者希望尽早地了解和分析产品设计因素之间的相互作用关系，以尽量减少产品设计后期的变更,提高产品设计的稳健性。

Taguchi稳健设计方法将设计过程划分为系统设计、参数设计、容差设计三个阶段，因此，又称三次设计[2]。该方法在产品设计阶段就考虑了其生命周期中存在的许多不确定性因素,并尽量减小它们对产品质量的影响,能够以低成本的方式保证产品质量,而不是寄希望于去消除或控制不确定性因素。Taguchi稳健设计方法自提出以来就得到了不断的发展和完善，但仍然存在其方法本身蕴含的局限性。目前稳健设计方法的应用研究大多只针对产品的参数设计阶段和容差设计阶段,以试验设计为基础,因而难以应用到产品系统设计中。Andersson[3]指出,系统设计阶段实际上已经决定了后续设计阶段产品的稳健性程度，参数设计和详细设计阶段难以纠正设计方案的缺点。此外,不考虑产品系统设计的稳健设计方法只从不确定参数的角度来探析系统达到稳健性的条件,而没有从理论的高度揭示影响系统稳健性的具体内在关系[4],因此,当产品因用户需求发生变化时系统原有的稳健特性将难以得到有效的保证。为了提高产品设计的稳健性，必须在系统设计阶段就开始考虑产品的稳健设计。

Zakarian等[5]提出了一种稳健系统开发框架,通过规定各子系统结构以使它们之间的作用最小化以及使系统对噪声因素不敏感来实现系统稳健。Lu等[6]提出了基于摄动敏感矩阵的稳健设计方法。张健等[4]提出了非线性条件下系统功能需求与结构特征参数、设计参数以及不可控因素之间的关系模型,建立了系统的稳健灵敏性矩阵,该方法主要还是面向参数设计阶段。在产品的系统设计阶段，大部分设计信息是不确定的，而是随着设计过程的深入而逐渐确定的，很难用传统的基于统计学的稳健模型来描述[7]。本文在已有研究成果的基础上,对机械系统设计的稳健性进行了较深入的分析和研究,以用户需求为切入点,定义并描述功能需求,以公理设计为指导框架，提出机械系统稳健性分析方法。

1　功能需求分析

机械系统稳健性分析的首要环节是对产品功能需求信息的准确获取与表达,产品功能需求建模是基于用户需求分析与企业自身能力考虑的。Kano[8]从用户的角度将需求划分为三种类型：基本型、期望型和兴奋型。用户需求特性无法直接转换成产品结构信息,需先转化为功能需求信息。在产品开发阶段只有充分地理解产品功能需求信息,将这些功能需求信息经分析、准确描述与表达并转化为产品结构信息，才有可能使所建立的产品概念模型有效地支持后续的产品设计。产品设计一旦完成后，就应具备一定的功能要求，用户对某一产品的需求归根结底是对其功能的需求。

借鉴Kano用户满意度模型，将产品功能要求(functional requirements,FRs)分为基本功能要求、期望功能要求和附加功能要求。

Yoshikawa[9]从知识处理和操作的角度出发,提出了一种设计过程规律的概念描述模型——通用设计理论(general design theory,GDT)。GDT将设计视为从功能空间到属性空间的映射过程，以元模型和元模型空间来表示逐步转化的过程。元模型用一组有限的属性来描述设计对象在设计过程特定阶段的状态、设计对象的组成实体以及实体间相互关联与依赖的关系，可较好地描述设计功能结构概念。文献[10]提出了一种关于产品方案设计的QUINT元模型,本文在此基础上对一些概念和术语进行了重新定义。

定义1对设计对象功能本质的抽象描述称为功能概念,记为FC。所有功能概念组成的集合称为功能空间,记为FCS。

定义2对设计对象结构本质的抽象描述称为结构概念,记为SC。所有结构概念组成的集合称为结构空间,记为SCS。

定义3满足设计环境、实现基本功能要求的功能概念称为基本功能概念,记为BFC。所有基本功能概念组成的集合称为基本功能空间,记为BFCS,且BFCS⊆FCS。

定义4满足期望功能要求的功能概念称为期望功能概念,记为EFC。所有期望功能概念组成的集合称为期望功能空间，记为EFCS，且EFCS⊆FCS。

定义5满足令用户意想不到的产品特征或功能的功能概念称为附加功能概念,记为AFC。所有附加功能概念组成的集合称为附加功能空间，记为AFCS，且AFCS⊆FCS。

定义6实现基本功能要求且满足约束条件的结构概念称为基本结构概念，记为BSC。所有基本结构概念组成的集合称为基本结构概念空间，记为BSCS，且BSCS⊆SCS。

三类功能空间的元素不是一成不变的,它们会随时间和技术的发展、价值观和消费理念等的变化而发生改变。现在的期望功能或许会转化为以后的基本功能,附加功能可能转化成期望功能。如起重机的超载限制、手机的上网功能,现已由期望功能逐渐变成基本功能了。

定义并描述以上概念的目的是为了更好地分析产品系统稳健性,任一产品或系统的基本功能要求首先必须得到很好的满足，然后才考虑期望功能要求和附加功能要求的实现,基本功能要求应只受基本结构概念影响,而不会因其他结构概念的变化而改变,且基本结构概念必须对期望功能要求和附加功能要求的变化不敏感，即有

(1)

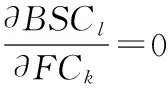
(2)

2　机械系统稳健性分析过程

以元模型为核心的GDT理论虽然可表示设计从功能空间到属性空间的逐步转化过程,但在映射过程中难以确定较为抽象的结构概念，对于较复杂的产品设计来说，其层次性和关联性都不够清晰[11]。公理设计通过Z字形逐步展开并在各个域中曲折映射，构建设计矩阵，可缩短设计中的迭代过程，减弱设计的耦合度，进而提高设计稳健性[12]。

按照公理设计方法,首先将实现产品的功能映射到产品结构上，确立产品概念结构，即设计参数(design parameters,DPs),结合设计者的经验知识，判断功能要求的分解和设计参数的选择是否满足设计要求，以及能否得到满意的结果。然后分析概念结构之间的关联关系，构建设计结构矩阵，确定耦合模块。上述设计过程模型如图1所示,其设计过程详细步骤如下。

图1　系统设计过程模型

(2)根据前一步确定的功能概念和技术要求，从知识库和设计者大脑里存储的有关结构的知识中，选择实现相应功能的结构，并形成结构概念空间SCS。由FCS到SCS的映射过程遵循公理设计方法的Z字形层级展开,充分考虑两者之间的匹配关系,尽可能满足独立公理要求。因耦合在许多实际设计过程中难以避免,此时可保留该部分的耦合性,或应用系统创新思维(systematic inventive thinking,SIT)或TRIZ进行初步的解耦。如果耦合性较强，也可将对应设计参数组合成一个耦合模块，然后再考虑该模块与其他模块之间的关联关系。

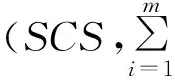
(4)根据功能-结构映射结构,建立产品设计矩阵。重排设计矩阵使之尽可能成为对角阵或下三角阵,然后借鉴文献[13]的方法将设计矩阵转换为设计结构矩阵(design structure matrix,DSM)。DSM的每一行表示系统其他设计参数对该行设计参数的物质、能量、结构、作用力等信息的输入关系，每一列表示该列的设计参数对其他各行设计参数的信息输出关系。将矩阵先分成两大块，一块是基本结构空间内的设计参数，另一块是其余设计参数，如图2所示。

图2　设计结构矩阵

(5)对设计结构矩阵进行重构。以BSCS中的设计参数为核心，应用聚类算法进行聚类，生成聚类模块。这些模块可以是耦合集,也可以是几个独立参数的组合体。这样，系统结构就被划分成几个相互之间具有较小依赖度的耦合模块，从而使系统结构具有较强的稳健性。根据公理设计理论，遵循两条公理的设计更易实现设计的稳健性，耦合弱的设计是更稳健的设计[14]。由此得到的矩阵称为系统稳健关联矩阵，如图3所示。

图3　系统稳健关联矩阵

3　稳健性分析的试验设计

系统稳健关联矩阵每个聚类模块可视为一个子系统或子结构,聚类模块之外的元素意味着子结构间有关联,使得各模块相互之间不能完全独立,即存在耦合性,从而影响系统的稳健性。如图3中的DP(6，2)、DP(10，6)和DP(11,4),分别表示模块1与模块2之间通过设计参数DP6和DP2、模块2与模块3之间通过DP10和DP6及模块1和模块3之间通过DP11和DP4进行关联。其中DP(6,2)表示模块1对模块2的影响，更具体地说，是模块1中的DP2对模块2中 的DP6施加影响，如果DP2因某种原因发生改变,则DP6也会产生相应的变化。DP(i,j)表示DPj对DPi的信息输入,即DPi所在的模块对DPj所在的模块的信息依赖。

由系统稳健关联矩阵可以确定模块间的所有关联参数，在产品系统稳健性分析中，这些关联参数可作为参数设计中的可控因素，以判断关联参数的变化对功能要求的影响程度。对于大多数实际工程问题，一般没有明确的公式来反映关联参数与系统响应及约束之间的关系，不能用显式函数的形式来表达，而是用试验或数值模拟来计算的。由于数值仿真或工程试验都较费时，因此在稳健设计中一般通过采集适当的样本、少量的试验或模拟、拟合系统响应方程来建立代理模型, 然后再进行稳健性分析。

正交试验设计[15]对因素的数量和水平没有严格的限制，因素之间有无交互作用均适用，在使用时按规范的表格可方便安排试验，一个三因素三水平的试验，按全因试验要求，须进行27 种组合的试验，且尚未考虑每一组合的重复数。若按L9(34)正交表安排试验，只需进行9次试验，显然大大减少了试验工作量。虽然正交试验中的最好点不一定是全因试验的最好点，但往往也是很好的点，尤其当只有一两个因素起主要作用时，它可保证主要因素的各种可能都不会遗漏，这点在试验初期筛选因素时非常重要。

对于图3所示的系统稳健关联矩阵，模块间的关联参数为DP2、DP4和DP6,即有3个可控因素。考虑这3个关联参数对设计目标的影响,以正交试验为例，安排可控因素的水平和试验次数，由于需观察各因素的影响关系，每个因素可取三水平，选正交表L9(34),如表1所示。图中的“0”、“-1”和“1”分别表示可控因素变动范围的中心值、下限值和上限值。

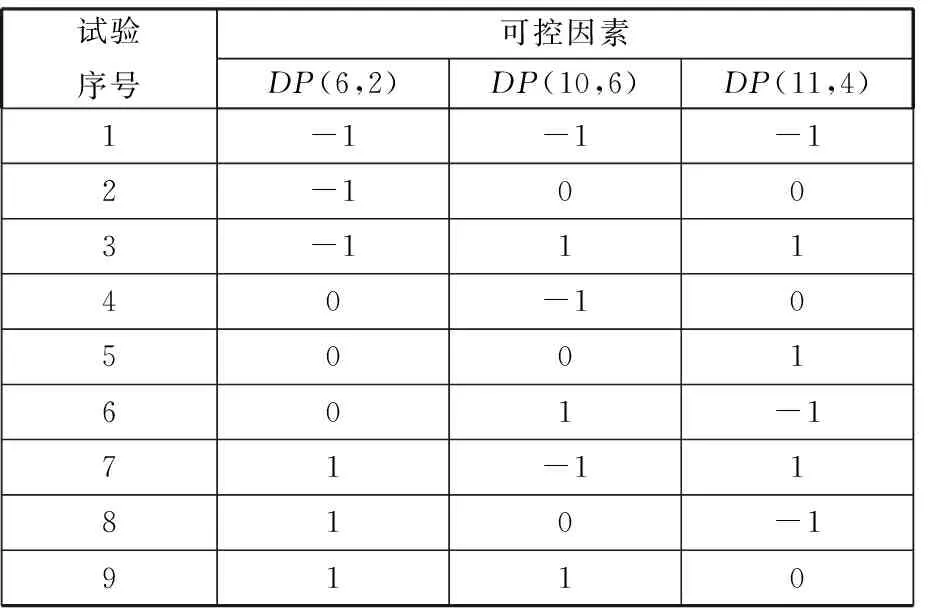
表1　正交试验安排

对于一些比较简单的问题，可以通过对试验结果的直观分析或利用方差分析技术，了解每个关联参数对设计目标影响的重要程度，确定最小耦合方案。对目标影响较大的关联参数，应对其进行控制与调整，从而提升机械产品系统的稳健性。对于需要较精确分析响应与参数关系的问题，一般情况下可采用能够准确洞察设计参数和响应之间关系的代理模型，如响应面模型,其因构造简单、计算量少、对样本数据需求较少等优点而得到了广泛应用, 但是对高度非线性问题拟合效果较差。而对于多维、非线性程度较高的问题,可采用Kriging模型，在有限区域内可对区域化变量求最优、线性、无偏内插估计值，具有平滑效应及估计方差最小的统计特征，可获得更高的精度。

4　实例分析

传统的起重机设计一般都是单件小批量设计模式,而且过多依赖设计人员的经验,不能很好地以低成本快速地响应用户个性化需求。目前起重机的模块化设计思想已引起许多企业的重视,即通过不同模块的组合,或调节一些设计参数,形成不同规格和系列的起重机，从而降低制造成本，提高通用化程度,以满足用户的多样化需求。为了使所设计的起重机具有更好地适应性，在其初期设计时就要考虑系统的稳健性。本文以通用双梁桥式起重机的起重小车为例,分析其稳健设计过程。

(1)设计要求描述为：该起重机用于电力部门厂房内，不太经常使用，有时起吊较大载荷，一般起吊中等载荷；要求有两台小车协调工作，其中主小车起重能力为32 t、货种规格为件杂货，要求运行平稳、工作可靠、有保护装置等；跨度31.5 m，起升高度22 m。设计计算任务是：根据用户要求和目的、使用环境、工作条件及现有设计规范，建立用户需求；确定起重机和机构工作级别，合理选择起重小车结构形式，确定小车机构的传动方案；通过计算，选择并确定驱动、传动、制动装置，使之满足起重机主要工作性能的要求，安全可靠地工作；同时要求结构简单、自重轻、维修保养方便等。起重小车的主要用户需求如表2所示。

表2　起重小车用户需求

(2)通过对用户需求的分析,由设计人员产生所有的功能概念。起重机械的主要任务是起重，再者就是扩大工作范围，提升速度和效率，保证安全操作。在形成功能概念空间FCS的同时，利用公理设计方法进行映射，得到如图4所示的功能分解图，其中左半部分表示的是功能要求FRs的层次结构，右半部分表示的是相对应的设计参数DPs的层次结构。由于针对系统设计,故对具体的参数在功能分解过程中没有具体阐述，如电动机、制动器、减速器等都未给出规格型号。

(3)根据起重小车各层级功能的要求和设计参数之间的关系，建立设计矩阵，经重新排列后的设计矩阵如图5所示。其中，在功能要求列中标记“b”为基本功能要求，标记“e”为期望功能要求，标记“a”为附加功能要求，即(FR111, FR112, FR113, FR121, FR122, FR123, FR124, FR211, FR212, FR213, FR221, FR222, FR31, FR33)∈BFCS,(FR114, FR115, FR214, FR215, FR32, FR41, FR42, FR43, FR44,FR45)∈EFCS,(FR223,FR46,FR47,FR48)∈AFCS。

(4)将起重小车的设计矩阵转化为设计结构矩阵，考虑各设计参数的物理结构关联关系，重构设计结构矩阵，再进行聚类，得到如图6所示的系统稳健关联矩阵。

图4　起重小车功能分解图

图5　重排后的起重小车设计矩阵

图6　起重小车的系统稳健关联矩阵

(5)关联参数的影响分析。从图6的系统稳健关联矩阵可以看出,DP(111,122)、DP(113,124)、DP(114,124)、DP(31,124)和DP(215,31)是游离于各模块外的元素,其数值的改变会引起相关模块内设计参数的变化，因此它们是影响系统稳健性的主要因素。特别是卷筒组中参数DP124,影响多个模块,其直径大小(DP(113,124)、DP(114,124))会影响扭矩和传动比，长度(DP(31,124))影响台车架的宽度，后者引起小车轨距变更，进而影响小车运行机构补偿轴的长度。卷筒的直径和长度不是相互独立的，两者有关联，由直径可推出长度。此外，小车车轮组在计算中也受起升机构各零部件的影响，但单独零部件的变化对其影响较小。鉴于此，主要对以上这些各模块间的关联参数进行稳健性分析，判断其对聚类模块影响的重要程度。这样总共有三个关联参数DP122、DP124和DP31，分别标记为A、B和C。因为卷筒直径根据钢丝绳直径和绳径比来确定,取值有一定的规范性，针对该起重机的工作条件，每个因素可取三水平,因关联参数与响应之间的关系为近似线性，且水平值较严格,故选用正交试验设计，如表3所示。

表3　起重小车关联参数水平表

(6)试验设计的目标是保证满足技术要求的前提下使得小车的结构紧凑、重量轻。结构紧凑体现为小车架的尺寸、整体高度及轨距。轨距的增大主要会引起桥架端梁重量增加；整体高度对大型起重机影响较大，因本文实例为中小型起重机的起重小车，暂可以不考虑整体高度的影响；小车架的尺寸直接影响到小车重量，它可以归到小车自重目标中。所以本文选择小车自重和轨距为目标，以考察关联参数的变化对目标的影响程度，其数值越小越好。进行正交试验,选正交表L9(34)，试验结果如表4所示。

(7)因关联参数较少且与响应之间的关系为近似线性,故可以通过对试验结果的直观分析来了解每个关联参数对设计目标影响的重要程度。试验结果直观分析如表4的下部分所示。画出各因素与试验结果的关系图，以每个因素的水平值为横坐标,该因素的水平均值为纵坐标,即可以看出各因素水平值对试验结果的影响趋势,如图7和图8所示。极差越大说明该因素对试验结果y值影响越大，该因素越重要。从图可看出卷筒直径对两个目标的影响都是最大的,台车架的横向尺寸影响次之,吊钩滑轮组只对小车重量有轻微影响。进一步计算分析：对于目标yⅠ,卷筒的极差与均值的比值可达16.67%,这说明其数值变化会导致yⅠ的显著变化;对于目标yⅡ,三个因素的极差与均值的比值分别为1.14%、2.65%和1.99%,整体影响都不算大,这是因为小车的重量与小车上所有设计参数都有关，三个关联参数的变化影响不突出，但对成本影响较大。因为卷筒直径变大，虽然使其长度缩短，从而引起轨距和端梁尺寸减小,但造成减速器等零部件的增大，这个成本会更高。卷筒直径的变化对两个指标的影响是不一致的，综合考虑，卷筒直径取450mm，另外两个关联参数就可以作为调节参数以满足用户需求，从而使起重小车系统具有更强的稳健性。

表4　试验结果及直观分析

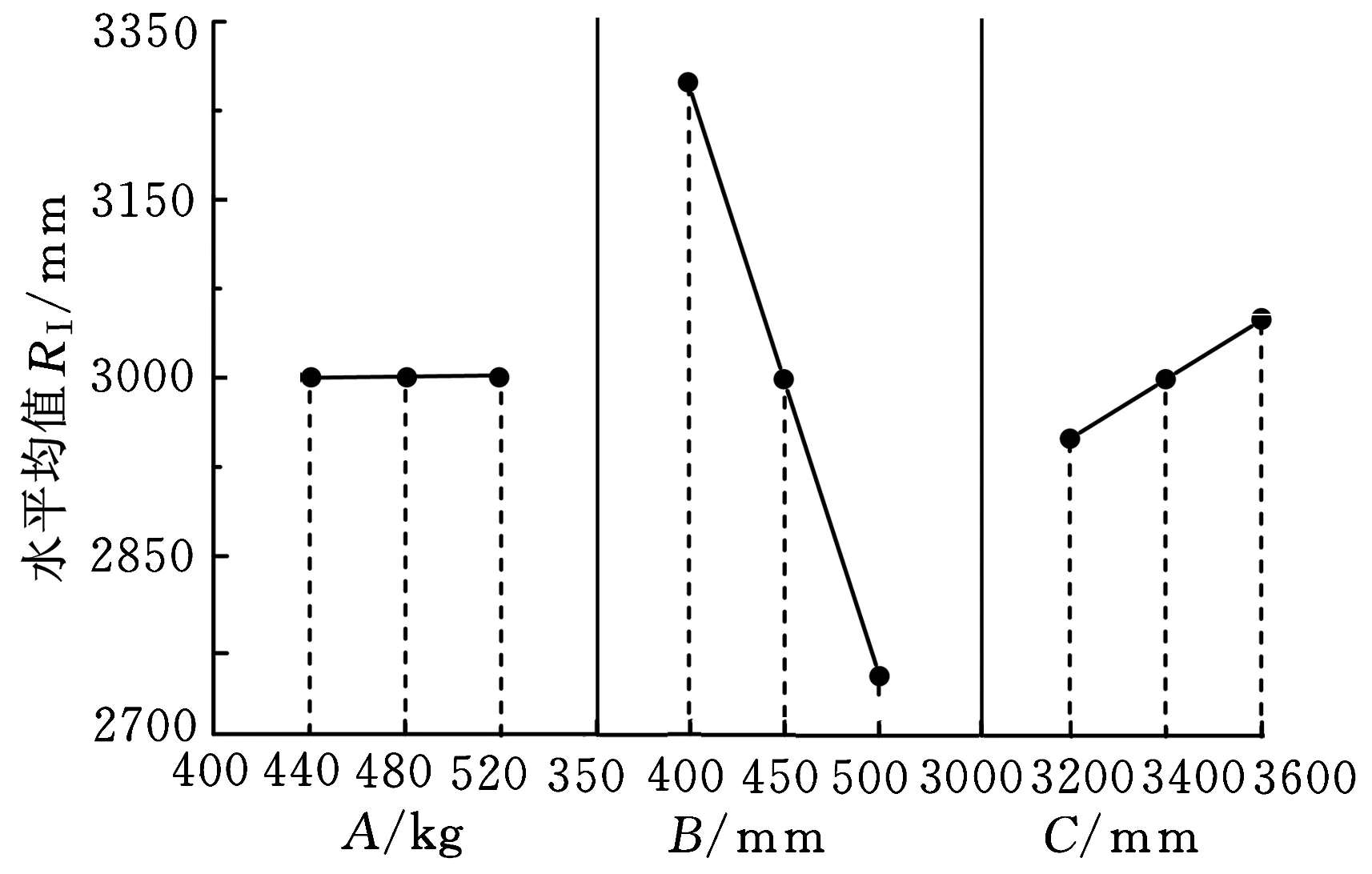
图7　因素水平变化对指标yⅠ的影响趋势图

图8　因素水平变化对指标yⅡ的影响趋势图

5　结束语

立足于用户需求，分析了产品功能需求,基于GDT元模型描述了设计功能-结构概念。以公理设计理论为指导框架，通过功能-结构的Z字形映射,并将实现基本功能要求的设计参数单独划分出来,然后将设计矩阵转换为设计结构矩阵并对其进行重构。以BSCS中的设计参数为核心，划分成几个相互之间具有较小依赖度的聚类耦合模块,再应用正交试验分析其对目标影响的重要程度,确定最小耦合方案,从而使系统结构具有较强的稳健性。应用所提出的系统稳健性分析方法进行了桥式起重机小车的设计，结果表明了该方法的可行性和有效性，可为设计者、产品工程师及研究者提供一种参考。

本文所提出的方法的实效性主要取决于各聚类块的耦合性，与技术人员的经验知识也有紧密关联。如果产品系统较复杂且耦合性很强，则可能会面临系统建模和数据分析计算量较大的问题。本文只是针对机械产品系统稳健性进行初步探讨，还不够全面，下一步将深入研究考虑噪声因素的影响以及选择合适的试验设计与代理模型，以使产品系统具有更高的稳健性。

[1]余俊,现代设计方法及应用[M].北京:中国标准出版社,2002.

[2]陈立周.稳健设计[M].北京:机械工业出版社,2000.[3]Andersson P.On Robust Design in the Conceptual Design Phase:A Qualitative Approach[J].Journal of Engineering Design,1997,8(1):75-89.

[4]张健,顾佩华,包能胜,等.非线性机械系统分析性稳健设计[J].机械工程学报,2009,45(10):207-215.Zhang Jian,Gu Paihua,Bao Nengsheng,et al.Analytical Robust Design of Non-linear Mechanical Systems[J].Journal of Mechanical Engineer,2009,45(10):207-215.

[5]Zakarian A, Knight J W, Baghdasaryan L. Modelling and Analysis of System Robustness [J]. Journal of Engineering Design, 2007,18(3):243-263.

[6]Lu X J, Li H X. Perturbation Theory Based Robust Design under Model Uncertainty [J]. Journal of Mechanical Design,2009,131(12):1-9.

[7]李涛,熊光楞,徐文胜,等.并行工程环境下的鲁棒设计[J]. 计算机集成制造系统,2001,7(4):30-35.

Li Tao,Xiong Guangleng, Xu Wensheng, et al. Robust Design within Concurrent Engineering Environment [J]. Computer Integrated Manufacturing Systems, 2001, 7(4): 30-35.

[8]Kano N. Attractive Quality Creation under Globalization[J]. China Quality, 2002(9):32-34.

[9]Yoshikawa H.General Design Theory and a CAD System[C]//The IFIP Working Group Working Conference on Man-machine Communication in CAD/CAM.Kyoto,1980:35-53.

[10]肖人彬，陶振武，刘勇. 智能设计原理与技术[M]. 北京：科学出版社，2006.

[11]张立彬, 史伟民, 鲍官军,等.基于公理设计的通用设计过程模型[J]. 机械工程学报,2010,46(23):166-173.

Zhang Libin,Shi Weiming,Bao Guanjun,et al.General Design Process Model Based on Axiomatic Design[J].Journal of Mechanical Engineer,2010,46(23):166-173.

[12]Suh N P.Axiomatic Design:Advances and Applications[M].New York:Oxford University Press,2001.

[13]肖人彬,程贤福,陈诚,等.基于公理设计和设计关联矩阵的产品平台设计新方法[J].机械工程学报,2012,48(11):93-103.

Xiao Renbin,Cheng Xianfu,Chen Cheng,et al.New Approach to Product Platform Design Based on Axiomatic Design and Design Relationship Matrix[J].Journal of Mechanical Engineer,2012,48(11):93-103.

[14]Xiao R B,Cheng X F.An Analytic Approach to the Relationship of Axiomatic Design and Robust Design[J].International Journal of Materials and Product Technology,2008,31(2/4):241-258.

[15]程贤福,袁竣萍,吴志强,等.基于双响应面法和BBD的车辆悬架系统稳健设计.华东交通大学学报,2012,29(5):1-6.

Cheng Xianfu,Yuan Junpin,Wu Zhiqiang,et al.Robust Design of the Vehicle Suspension System Based on Dual Response Surface Methodology and BBD[J].Journal of East China Jiaotong University,2012,29(5):1-6.

(编辑袁兴玲)

Axiomatic Design-based Analysis of Mechanical System Robustness and Its Applications

Cheng XianfuLi JunXu YounanZhu Qihang

East China Jiaotong University,Nanchang,330013

In the process of system modeling,the customer needs were transformed into functional requirements,which were expressed with metamodel.Based on independent axiom and zigzag mapping mode of axiomatic design,the functional requirements were mapped to design parameters,and the design matrix was created,which was then converted into design structure matrix by identifying the relation among functional requirements and the sensitivity of functional requirements to design parameters.Clustering algorithm was utilized to cluster the design parameters and to group the system components into modules in design structure matrix, and the interface among modules could be identified and system robustness interaction matrix was developed.Then the interaction parameters were considered as controllable factors, and experimental design techniques were utilized to analyze the fluency of interaction parameters on the design goal,if any,that mought result in a robust system.The applications of the approach were illustrated with crane example of the design of a crab system,which proves its effectiveness and feasibility.

robustness analysis;design of experiment;axiomatic design;mechanical system

2013-12-20

国家自然科学基金资助项目(51165007,71462007);江西省自然科学基金资助项目(20132BAB206025)

TH122DOI：10.3969/j.issn.1004-132X.2015.06.003

程贤福,男,1975年生。华东交通大学机电工程学院博士、副教授。主要研究方向为稳健设计与产品族规划。发表论文60多篇。李骏,男,1969年生。华东交通大学机电工程学院博士、教授。徐尤南,男,1965年生。华东交通大学机电工程学院博士、教授。朱启航,男,1990年生。华东交通大学机电工程学院硕士研究生。