基于加速度反馈的单输入时不变线性离散系统极点配置

梁　青　王　珍　潘金文　彭　程

中国科学技术大学，合肥，230026

基于加速度反馈的单输入时不变线性离散系统极点配置

梁青王珍潘金文彭程

中国科学技术大学，合肥，230026

讨论了单输入时不变线性离散系统用加速度信号进行极点配置的可行性。首先, 给出了用状态差分反馈进行极点配置的定理和算法; 其次, 用3个仿真实例验证了该算法的有效性；最后, 在隔振器实验平台上验证了用加速度信号进行反馈控制的可行性。

线性离散系统; 加速度反馈; 状态微分反馈; 状态差分反馈; 极点配置

0　引言

极点配置是线性系统设计最重要的工具之一[1-4]。用状态反馈实现极点配置是用状态空间描述的线性系统(连续或离散)控制器设计的有效手段,学者们对此已经做了大量研究工作[1-2,4-7]，在这些研究中,假设系统的全部状态可测,即全状态反馈。对于状态不能直接可测的系统,通过构建全维或降维渐近状态观测器得到系统状态的观测值,并用观测状态实现状态反馈,增加系统的阶次。对于线性连续系统,一种特殊的状态反馈——状态微分反馈近年来受到学者们的广泛关注,其实质是利用加速度信号实现反馈,这方面已有较多的研究成果[8-15]。文献[12-13]分别讨论了单输入和多输入线性系统极点配置问题的求解算法。文献[14]给出了用状态微分反馈以及输出微分反馈设计LQR(linear quadratic regulator)的方法。而对于线性离散系统,利用加速信号实现状态反馈的研究还未见报道。

在经典控制理论中,微分可以增加系统阻尼,为实现预期控制目标，微分反馈有时是必不可少的[8],而研究状态微分反馈的另一个动机来源于减振机械系统[9-11],其主要的传感器是加速度计。由加速度可以很容易地在可接受的误差范围内获得速度信号,但由于加速度计的测量误差及测量噪声干扰,由加速度获得位移信号会存在较大的误差，因而可用于反馈的信号只有加速度和速度信号,它们分别对应于机械系统速度和位移的微分,即状态微分。在离散系统框架下,加速度和速度对应于状态的差分。

本文主要研究单输入时不变线性离散系统的加速度反馈极点配置问题。首先对问题进行数学描述，使用线性变换将一般线性离散系统变换为具有能控标准型的系统；其次讨论了能控标准型系统状态差分反馈极点配置问题以及一般线性离散系统状态差分反馈极点配置问题的解,给出了状态差分反馈极点配置定理。再次,给出了减振器系统、球杆系统以及双积分系统的状态差分反馈控制仿真结果,验证了所提算法的正确性和有效性。最后,在实际隔振器实验平台上验证了用加速度信号进行反馈控制的可行性。

1　加速度反馈极点配置问题的描述与能控标准型系统

1.1问题描述

考虑能控的单输入时不变线性离散系统为

x(k+1)=Gx(k)+hu(k)x(0)=x0

(1)

其中，x(k)是状态变量,x(k)∈Rn×1;u(k)是控制量,u(k)∈R1×1;G是系统矩阵,G∈Rn×n;h是控制增益向量,h∈Rn×1。用加速度的采样值实现反馈控制，即

u(k)=-ksa(k)

(2)

其中，ks是加速度反馈增益向量,ks∈R1×n;a(k)为加速度的采样值以及计算得到的速度采样值,a(k)∈Rn×1。为研究其极点配置问题,有

u(k)=-ks(x(k+1)-x(k))/Ts=

-k(x(k+1)-x(k))

(3)

其中,Ts是采样周期;k是差分反馈增益,k=(k0,k1,…,kn-1),并有ks=kTs。则极点配置问题变成状态差分增益向量k的求解问题。系统矩阵G的特征多项式为

det(zI-G)=zn+g0+g1z+g2z2+…+gn-1zn-1

(4)

其中,z为变换算子，I为单位矩阵,I∈Rn×n。定义g(g∈R1×n)为系统矩阵G的特征多项式系数，g=[g0g1…gn-1]。设计的目标是通过式(3)的状态差分反馈将闭环系统的极点配置到期望的位置上，以稳定系统并使系统具有期望的动态特性。此时,闭环系统为

x(k+1)=Gx(k)-hk(x(k+1)-x(k))

(5)

通过选择k使矩阵I+hk满秩,则闭环系统可以写成

x(k+1)=(I+hk)-1(G+hk)x(k)

(6)

闭环系统的特征多项式为

det(zI-Gc)=det(zI-(I+hk)-1(G+hk))

(7)

Gc=(I+hk)-1(G+hk)

其中,Gc是闭环系统的系统矩阵。设计的问题就是通过寻找状态差分反馈增益向量k，使得闭环系统(式(6))的极点在期望的位置上。

1.2能控标准型系统

采用文献[12]的算法,对原系统(式(1))进行非奇异状态变换:

(8)

其中,z(k)是变换后的状态向量,z(k)∈Rn×1;Q-1是变换矩阵,Q-1∈Rn×n,设变换后的系统矩阵为Gf,控制增益向量为hf,则有

(9)

变换矩阵的选取如下:

Q-1=[qq Gq G2…q Gn-1]T

(10)

(11)

(12)

其中,向量q∈R1×n；en是单位向量；Mc是原系统(式(1))的能控性矩阵。

变换后的系统是下友型能控标准型系统：

z(k+1)=Gfz(k)+hfu(k)

(13)

该下友型能控标准型系统能够简化基于状态差分反馈控制的极点配置问题的求解过程。

2　极点配置问题的解

2.1下友型能控标准型系统问题的解

系统(式(13))的状态差分反馈为

u(k)=-l(z(k+1)-z(k))

(14)

l=[l0l1…ln]

式中，l为状态差分反馈向量；li为第i个状态差分反馈系数，i=0,1,…,n。

其中,重写控制律(式(14))为

u(k)=-l0(z1(k+1)-z1(k))-l1(z2(k+1)-

z2(k))-…-ln-1(zn(k+1)-zn(k))

(15)

由式(13)易得

(16)

将式(15)代入式(16)的最后一式并利用状态之间的关系,可得

zn(k+1)=-g0z1(k)-g1z2(k)-…-gn-1zn(k)+

l0z1(k)-(l0-l1)z2(k)-(l1-l2)z3(k)-

…-ln-1zn(k+1)=-(g0-l0)z1(k)-

(g1+l0-l1)z2(k)-(g2+l1-l2)z3(k)-

…-(gn-1+ln-2-ln-1)zn(k)-ln-1zn(k+1)

(17)

若1+ln-1≠0,则式(17)可以写成标准状态方程：

zn(k+1)=-(1+ln-1)-1[(g0-l0)z1(k)+

(g1+l0-l1)z2(k)+…+(gn-1+ln-2-ln-1)zn(k)]

(18)

则下友型标准型的状态差分反馈闭环系统为

z(k+1)=Gcfz(k)

(19)

Gcf=

由闭环系统(式(6))和状态变换方程(式(8)),可以得到下友型能控标准型的闭环系统矩阵与原闭环系统矩阵的关系：

(20)

下友型能控标准型状态差分反馈闭环系统(式(19))的特征多项式为

det(zI-Gcf)=(1+ln-1)-1[g0-l0+(g1+l0-l1)z+

…+(gn-1+ln-2-ln-1)zn-1]+zn

(21)

期望极点可以由特征方程的根给出,也可以由特征多项式系数给出,即

d(z)=(z-λ1)(z-λ2)…(z-λn)=

zn+d0+d1z+d2z2+…+dn-1zn-1

(22)

其中,特征值λi∈C1×1，i=1,2,…,n,若有复根,则必须以共轭形式成对出现。期望特征多项式的系数d∈R1×n且d=[d0d1…dn-1]。由式(21)和式(22)关于z的多项式对应项系数相等可以得到

(23)

因为1+ln-1≠0,整理可得

(24)

写成矩阵形式如下：

DlT=gT-dT

(25)

其中,系数矩阵D为

矩阵D的行列式为

(26)

其中,e∈Rn×1且e=[111…1]T。

式(25)的解分以下两种情况讨论:

(1)det D≠0。即矩阵D是非奇异的,由式(25)可得下友型能控标准型极点配置问题的解：

l=(g-d)D-T

(27)

事实上,不需要矩阵求逆,也可直接得到式(24)的解。将式(24)各式的左边依次相加,右边依次相加可得

(1+de)ln-1=(g-d)e

(28)

解得

ln-1=(g-d)e/(1+de)

(29)

求得ln-1后再倒序求解式(24),即求解顺序为l0,l1,…,ln-2,可得

(30)

γ=1+ln-1

(2)det D=0。即矩阵D是奇异的,为使式(28)有解,必须满足

ge=de

(31)

这就表明,ge+1=0和de+1=0必须同时成立。由式(28)可知,此时ln-1是自由的,只需选择ln-1≠-1即可。此时式(24)的解为

(32)

若1+ge≠0且1+de≠0,则

(33)

式(33)表明，原系统的所有特征根均不为1,这意味着对于任意的输入原系统都有一个平衡点xeq。在式(1)中令x(k+1)=x(k)=xeq，解得

xeq=(I-G)-1hu

(34)

对于期望的闭环系统,也有相同的结论。这表明,状态差分反馈无需考虑系统有无平衡点。

2.2一般系统的解

上文针对具有下友型能控标准型的单输入时不变线性离散系统,求得了基于状态差分反馈的问题的解,下面求一般单输入时不变线性离散系统的解。

将式(8)代入式(14)可得

u(k)=-l(z(k+1)-z(k))=

-l Q-1(x(k+1)-x(k))

(35)

对比式(3)和式(35)可得原系统(式(1))的状态差分反馈控制问题的解：

k=l Q-1

(36)

推导状态差分反馈增益向量k的具体表达式。有

l=(g-γd)Mr

(37)

其中，Mr为上三角矩阵。得到状态差分反馈增益向量：

k=(g-γd)MrQ-1

(38)

加速度反馈增益向量为

ks=Ts(g-γd)MrQ-1

(39)

由上述讨论得出以下定理。

定理1若系统(式(1))能控且不含极点z=1, 则可通过状态差分反馈(式(3))在z平面任意配置极点到期望的位置上。

定理2若系统(式(1))能控且含极点z=1,则可通过状态差分反馈(式(3))在z平面任意配置极点到至少含有以z=1为其中一个极点的期望位置上。

3　仿真实例

例1考虑减振机械系统,其动态方程为

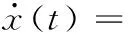
其中，各参数的具体意义见文献[12]。易知原系统是一个开环渐近稳定的系统, 但系统达到平衡状态的时间较长。设计状态差分反馈使闭环系统稳定且零输入响应的暂态过程时间缩短。取采样周期Ts=0.5 ms,离散化后的系统矩阵和控制量增益分别为

h=[00-5×10-65×10-5]T

闭环系统期望极点

λ1,2=exp(Ts(-5±65i))

初始状态取

x0=[0.050.050.20.2]T

解得加速度反馈增益

ks=[260.3388294.1277-1.2023-0.2872]

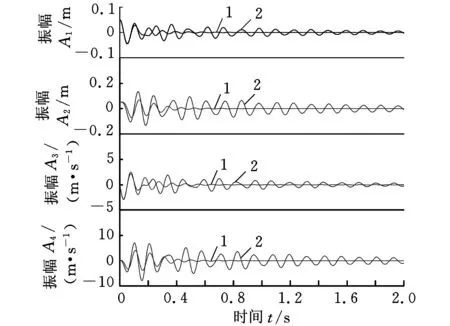
由图1可以看出,闭环系统的瞬态响应明显优于开环系统;由图2可以看出,加速度信号(a3(t),a4(t))的瞬态值较大,而速度信号(a1(t),a2(t))的瞬态值不至于过大;图3所示为控制信号的变化曲线。

1.闭环系统　2.原系统图1　原系统和闭环系统零输入响应(例1)

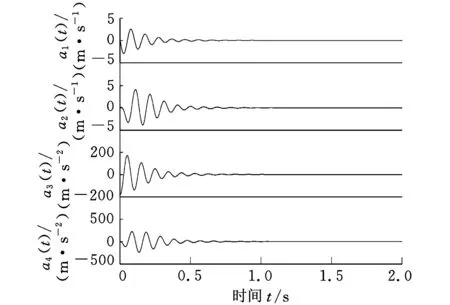
图2　状态差分的理论值(例1)

图3　控制信号(例1)

例2考虑球杆系统,动态方程为

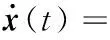
其中，各u(t)参数的具体意义见文献[12]。易知原系统是一个开环不稳定的系统,设计状态差分反馈使得闭环系统渐近稳定且暂态过程尽可能短。取采样周期Ts=5 ms,离散化后的系统矩阵和控制量增益分别为

h=[00.004 9500]T

闭环系统期望极点为

λ1,2=exp(Ts(-3±i))

λ3=-2Tsλ4=-5Ts

解得加速度反馈增益

ks=[-0.1064-1.010512.85176.1787]

初始状态为

x0=[0.1 0.1 0.01 0.01]T

由图4可以看出,闭环系统渐近稳定且能较快到达平衡状态;图5所示为状态差分的理论值;图6所示为控制信号的变化曲线。仿真结果表明,对于开环不稳定的系统,本文方法也是有效的。

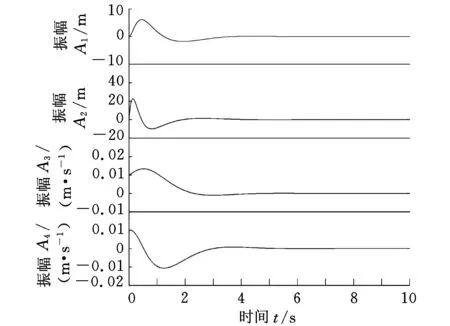
图4　闭环系统零输入响应(例2)

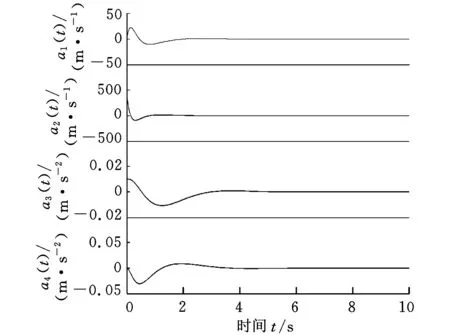
图5　状态差分的理论值(例2)

图6　控制信号(例2)

例3考虑双积分系统,动态方程为

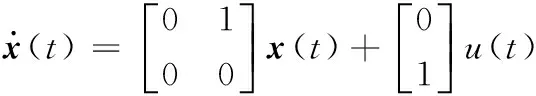
取采样周期Ts=5 ms,离散化后的系统矩阵和控制量增益分别为

图7～图9的意义与例2相同,从图7可以看出,闭环系统仍然具有一阶积分特性,即状态差分反馈不能完全去除原系统在z=1处的极点,从而验证了定理2。

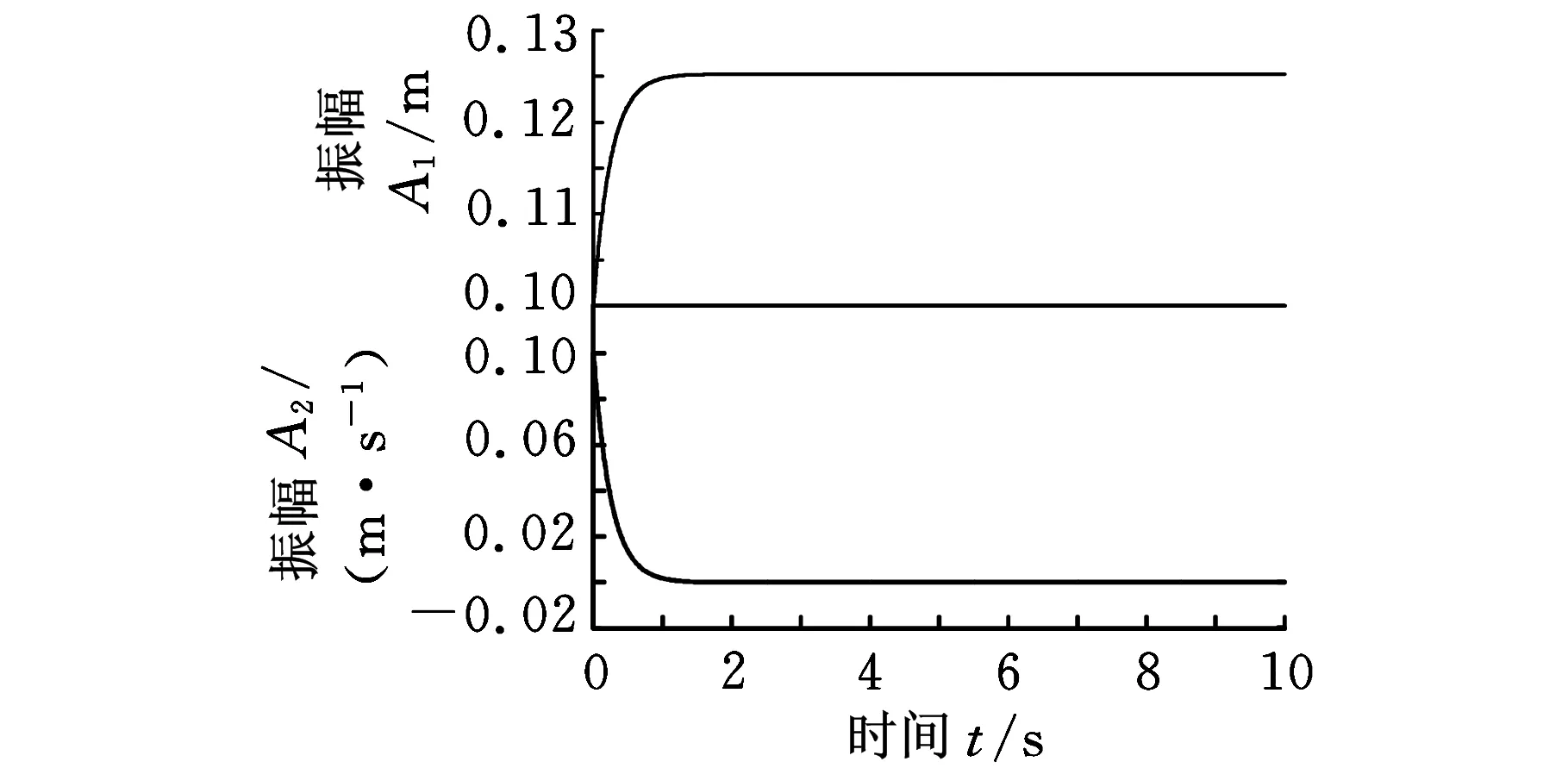
图7　闭环系统零输入响应(例3)

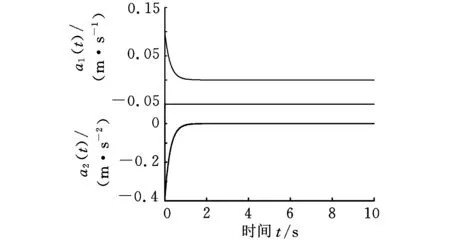
图8　状态差分的理论值(例3)

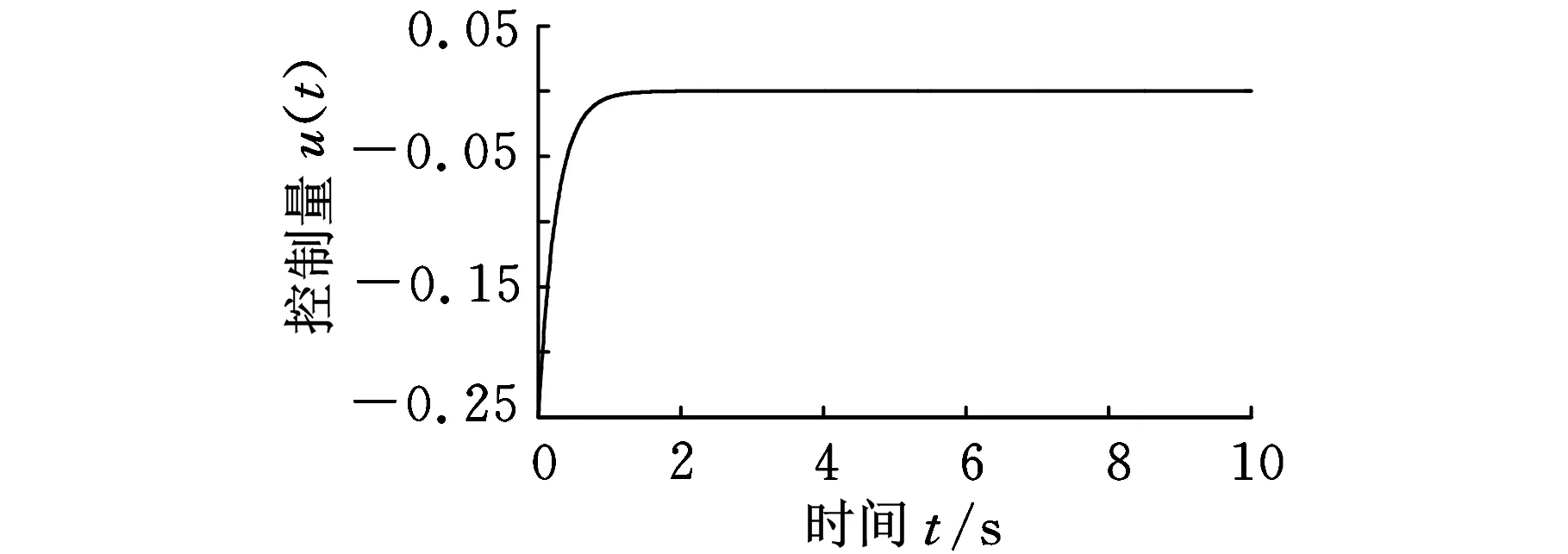
图9　控制信号(例3)

4　实验结果

本课题组一直致力于隔振器方面的研究。图10所示是本课题组自主研发的磁悬浮隔振系统[16]。

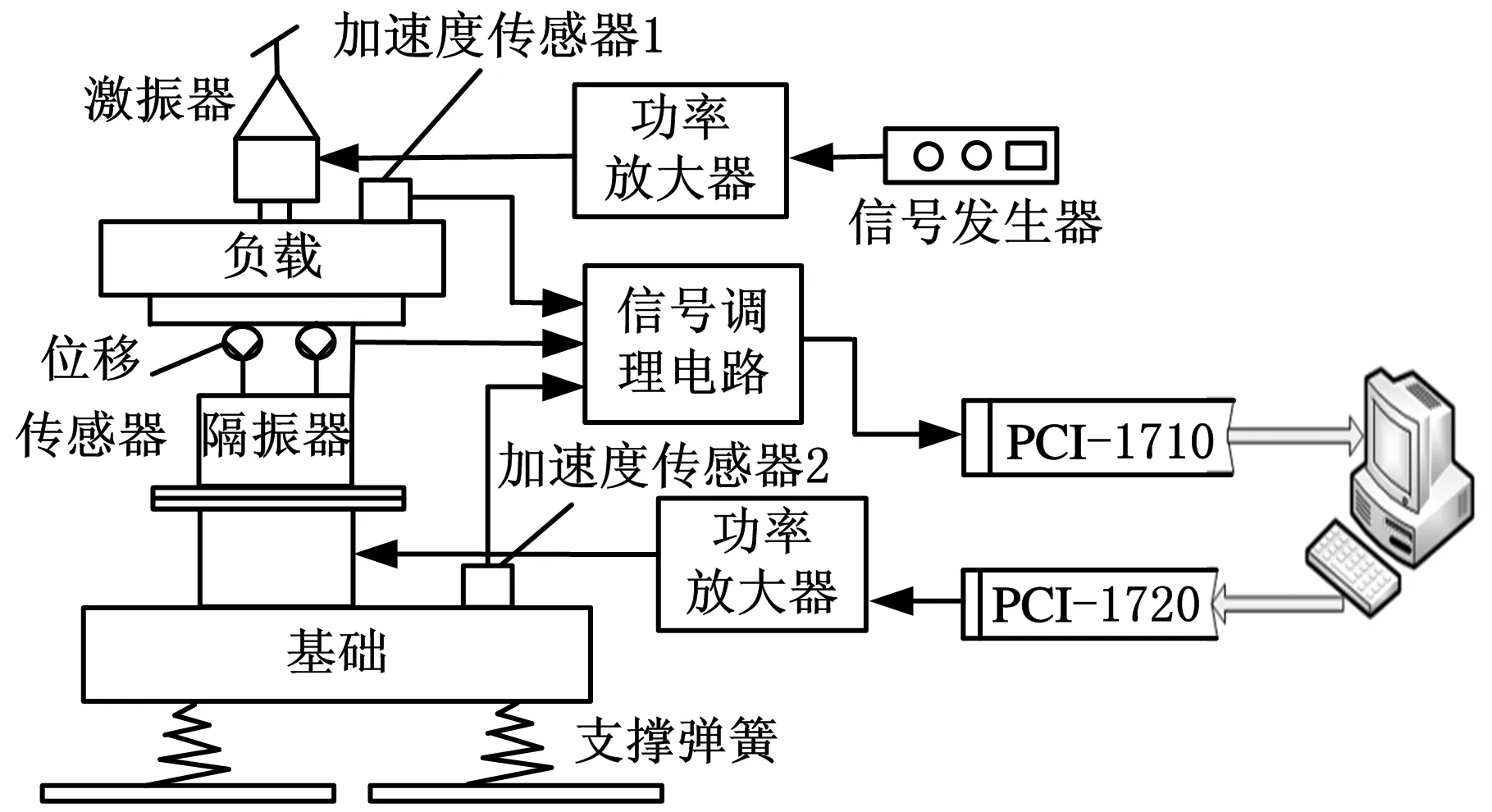
图10　磁悬浮隔振器实验平台原理图

由图10可以看出,负载与基础的加速度可以分别由加速度传感器1和2直接测量获得,可以直接用于反馈控制。为验证加速度反馈的可行性,振动主动控制的目标是当负载或基础偏离自身平衡位置时,电磁作动器按照一定的规律产生电磁力，从而使负载和基础分别回到自身的平衡位置。在对电磁作动器输出的电磁力与基础及速度的关系进行建模时,选择负载位移、负载速度、基础位移、基础速度作为状态,则由负载加速度得到的负载速度信号、负载加速度，由基础加速度得到的基础速度信号以及基础加速度信号就对应于状态的微分,即可直接利用加速度信号实现反馈控制而无需构建状态观测器。上述系统可以用图11所示模型来描述。

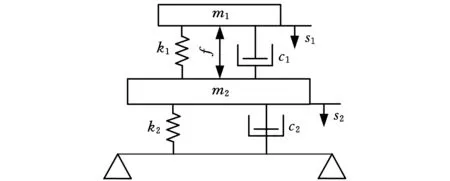
图11　电磁作动器作用下磁悬浮隔振系统原理图

系统的状态空间表达式为

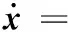
其中,u为电磁力,s1为负载位移,s2为基础位移。磁悬浮隔振器中各元件的标称值见表1。

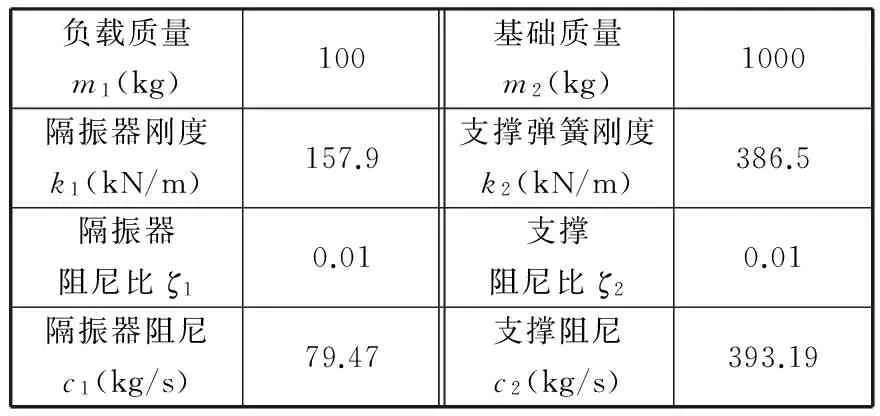
表1　磁悬浮隔振器元件标称值

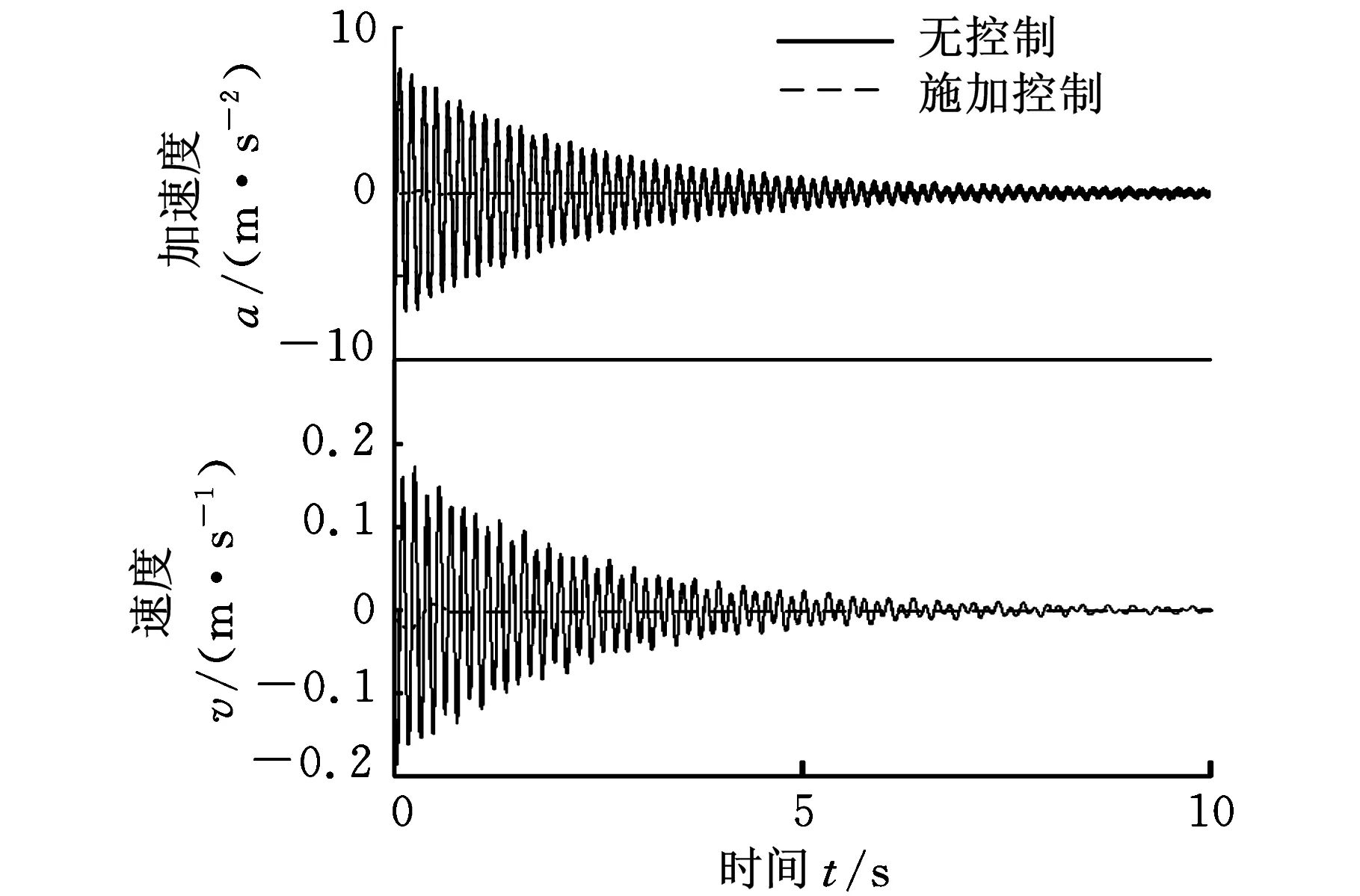
(a)负载的加速度测量值与速度重构值

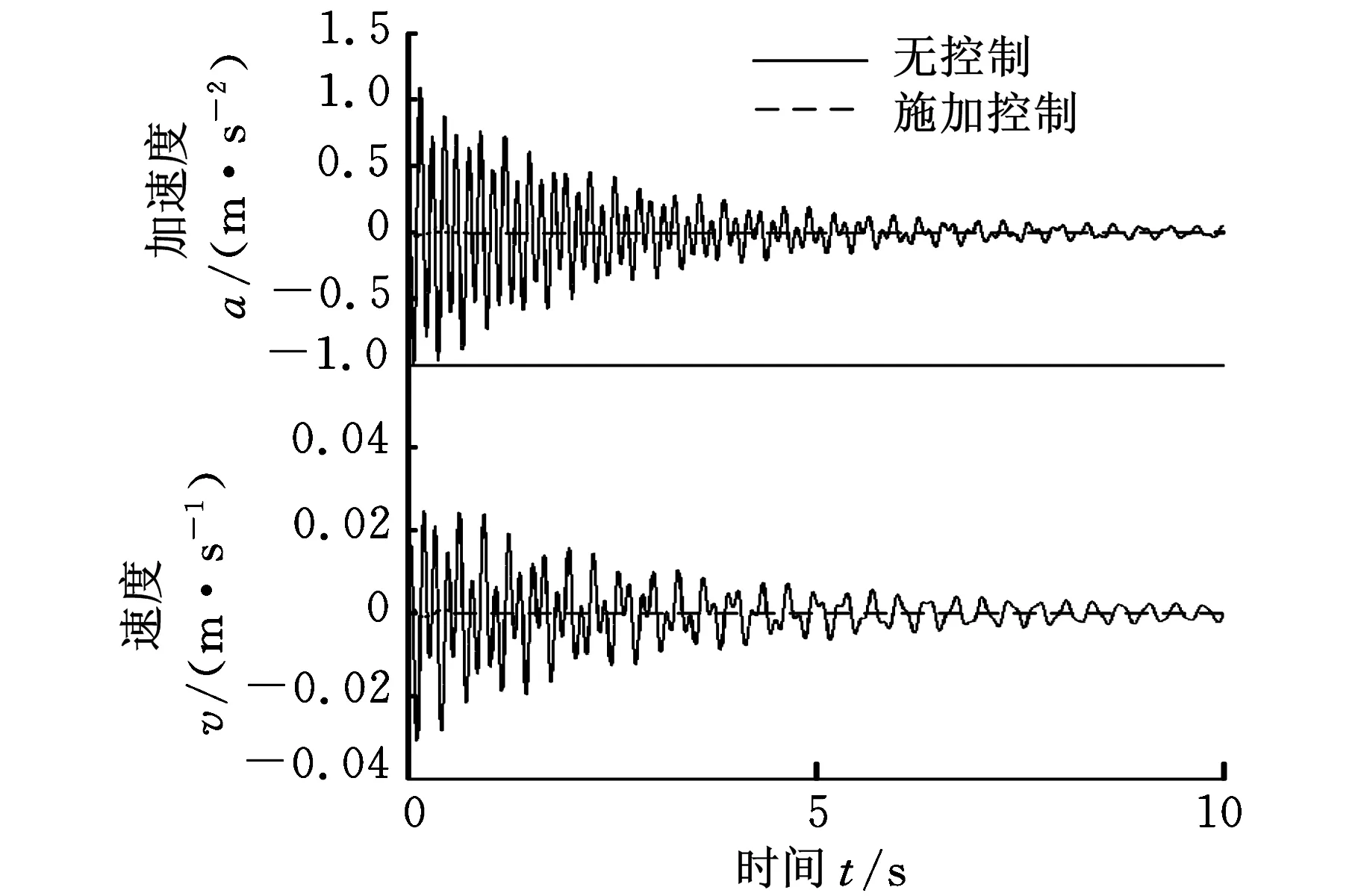
(b)基础的加速度测量值与速度重构值图12　系统无控制与施加控制时负载与基础的加速度测量值与速度重构值

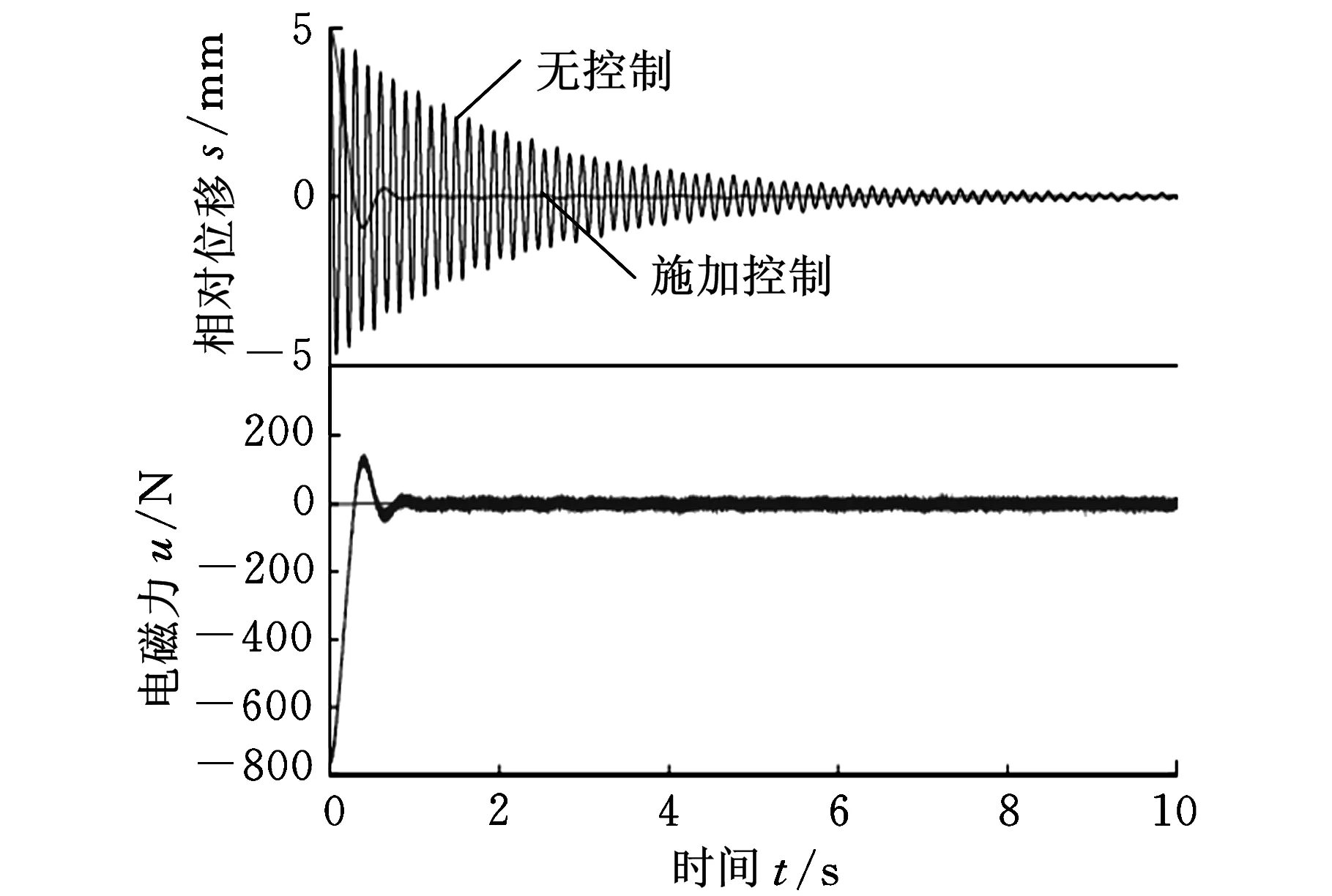
图13　负载与基础的相对位移和电磁力变化曲线

初始时,手动使负载稍微偏离自身平衡位置,施加控制与不施加控制的变量对比见图12和图13。控制方法采用本文所提方法,采样周期取Ts=0.2 ms,闭环系统极点取λ1,2=exp(Ts(-5±15i)),λ3,4=exp(Ts(-7±10i))。由图12可知,若不施加控制,负载和基础都需要较长时间才能回到平衡位置；而使用加速度信号作为反馈的控制,可以使系统尽快回到平衡位置,该结果验证了加速度反馈的有效性。

5　结语

本文从单输入时不变线性系统的离散形式出发,阐述了用加速度反馈配置系统极点的实际意义,通过转化将其归结为用状态的差分作反馈的增益求取问题。详细给出了下友型能控标准型系统基于状态差分反馈极点配置问题的解的求取过程,并通过状态变换得到一般时不变线性离散系统基于状态差分反馈极点配置问题的解。由求解过程的讨论得到基于状态差分反馈的极点配置定理和算法。所举的3个典型实例和隔振器实验都验证了本文方法的可行性和有效性。

[1]DorfRC,BishopRH.ModernControlSystems[M].London:PrenticeHall,2011.

[2]李嗣福.计算机控制基础[M].合肥:中国科学技术大学出版社, 2006.

[3]WonhamW.OnPoleAssignmentinMulti-inputControllableLinearSystems[J].IEEETransactionsonAutomaticControl, 1967,12(6): 660-665.

[4]周兆敏.用极点配置方法设计滑模控制器[J].信息与控制,1988,17(4): 47-49.

ZhouZhaomin.SlidingModeControllerDesignbyUsingPolePlacementmethod[J].InformationandControl,1988,17(4): 47-49.

[5]段学超,袁俊,满曰刚.两轮自平衡机器人的动力学建模与模糊进化极点配置控制[J].信息与控制, 2013, 42(2):189-195.

DuanXuechao,YuanJun,ManYuegang.DynamicalModelingandFuzzyEvolutionaryPolePlacementControlforaTwo-wheeledSelfbalancingRobot[J].InformationandControl, 2013, 42(2):189-195.

[6]KautskyJ,NicholsNK,VanDP.RobustPoleAssignmentinLinearStateFeedback[J].InternationalJournalofControl, 1985,41(5):1129-1155.

[7]GaoZunhai,YeXichen.Pole-placementforMulti-inputLinearSystemsbyStateFeedbackorState-derivativeFeedback[J].AdvancedMaterialsResearch, 2013,605/607:1765-1768.

[8]LewisF,SyrmosV.AGeometricTheoryforDerivativeFeedback[J].IEEETransactionsonAutomaticControl, 1991, 36(9):1111-1116.

[9]OlgacN,ElmaliH,HosekM,etal.ActiveVibrationControlofDistributedSystemsUsingDelayedResonatorwithAccelerationFeedback[J].JournalofDynamicSystems,MeasurementandControl, 1997, 119(3): 380-389.

[10]KwakSK,WashingtonG,YedavalliRK.AccelerationFeedback-basedActiveandPassiveVibrationControlofLandingGearComponents[J].JournalofAerospaceEngineering, 2002,15(1): 1-9.

[11]ChattwejeeS.VibrationControlbyRecursiveTime-delayedAccelerationFeedback[J].JournalofSoundandVibration, 2008,317(1): 67-90.

[12]AbdelazizTHS,ValaekM.Pole-placementforSISOLinearSystemsbyState-derivativeFeedback[J].IEEProceedings:ControlTheoryandApplications, 2004, 151(4): 377-385.

[13]AbdelazizTHS,ValaekM.DirectAlgorithmforPolePlacementbyState-derivativeFeedbackforMulti-inputLinearSystems-NonsingularCase[J].Kybernetika, 2005, 41(5): 637-660.

[14]AbdelazizTHS,ValaekM.StateDerivativeFeedbackbyLQRforLinearTime-invariantSystems[C]//Proceedingsofthe16thTriennialWorldCongressofInternationalFederationofAutomaticControl.Prague, 2005:1-6.

[15]AmriI,SoudaniD,BenrejebM.RobustState-derivativeFeedbackLMI-basedDesignsforTime-varyingDelaySystem[C]//Proceedingsofthe2011InternationalConferenceonCommunications,ComputingandControlApplications.Hammamet, 2011.

[16]孟令雷.磁悬浮隔振器的建模与控制[D].合肥：中国科学技术大学,2009.

(编辑陈勇)

Pole Placement for Single Input Linear Time-invariant Discrete Systems by Acceleration Feedback

Liang QingWang ZhenPan JinwenPeng Cheng

University of Science and Technology of China,Hefei,230026

The feasibility of pole placement by acceleration signal for single input time-invariant linear discrete systems was discussed. Firstly, the theorems and algorithms of pole placement by state-difference were provided. Secondly, the effectiveness of the proposed method was validated by three simulation examples. Finally, an experimental platform was setup to validate the feasibility of the proposed method.

linear discrete system; acceleration feedback; state-derivative feedback; state-difference feedback; pole placement

2013-09-16

国家自然科学基金资助项目(61004017)；中国科学技术大学青年创新基金资助项目(WK2100100016)

TP273< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.08.020

梁青，男，1961年生。中国科学技术大学信息科学技术学院副教授。主要研究方向为飞行器制导与控制、系统仿真、智能信息处理等。王珍，女，1989年生。中国科学技术大学信息科学技术学院硕士研究生。潘金文，男，1989年生。中国科学技术大学信息科学技术学院博士研究生。彭程，男，1978年生。中国科学技术大学信息科学技术学院副教授。