考虑车内振动的动力总成悬置系统多目标优化

陈　剑　史韦意　蒋丰鑫　曾维俊　沈忠亮　汪一峰

合肥工业大学,合肥,230009

考虑车内振动的动力总成悬置系统多目标优化

陈剑史韦意蒋丰鑫曾维俊沈忠亮汪一峰

合肥工业大学,合肥,230009

以实际工况下的测试数据为基础，建立了简化的车内振动传递路径分析模型。在此基础上，以发动机悬置刚度为设计变量，综合考虑悬置系统能量解耦和车内振动，建立了基于灰色粒子群优化算法的多目标优化模型。并以某型卡车为例，进行了多目标优化求解。实验和优化结果表明,在得到较好能量解耦的同时,降低了车内振动,实现了能量解耦和车内低振动的优化匹配。

动力总成悬置系统;传递路径分析;灰色粒群算法;蒙特卡罗法

0　引言

动力总成悬置系统是汽车振动噪声研究的一个重要对象,它不仅起到支撑动力总成部件的作用,还扮演着隔离振动的角色。悬置系统设计的好坏直接影响着整车的NVH性能[1],合理的悬置系统对于汽车整车的减振降噪具有重要的作用。因此,对动力总成悬置系统的优化设计显得尤为重要。

动力总成悬置的设计与开发中，广泛将能量解耦或部分解耦作为主要的优化目标，但该方法自身存在不足。因为解耦率指标由悬置的各个方向刚度的比例关系确定，相同的解耦率指标对应着相同比例的悬置刚度[2],但每一组刚度可能不同,这样悬置系统产生的车内振动情况不一致。车辆NVH性能的衡量应重点关注车辆驾乘人员的环境-驾驶室的振动噪声情况,因此单纯保证系统具有较好的解耦率指标是不完善的。

本文综合考虑悬置系统能量解耦与车内振动,结合整车传递路径分析方法,建立了基于灰色粒子群优化算法的动力总成悬置系统多目标优化模型。以某型卡车为例，进行了悬置系统参数的优化求解，对优化后的悬置参数应用蒙特卡罗法进行了稳健性分析，并从发动机刚体模态和车内振动优化效果两方面对优化模型进行了实验验证。结果表明，该方法在较好地实现能量解耦的同时，降低了车内振动水平，较好地实现了能量解耦和车内低振动的匹配。

1　动力总成悬置系统模型及能量解耦

1.1悬置系统动力学建模

将动力总成和车架视为刚体,动力总成悬置系统可简化为具有六自由度的振动系统。四点悬置的动力总成悬置系统的动力学模型如图1所示。假设动力总成置于相互正交的OXYZ坐标系中,原点O为静止时动力总成的质心。刚体的运动具有6个自由度，即沿3个坐标轴的平动以及绕3个坐标轴的转动，其广义坐标为

q=[xyzθxθyθz]T

(1)

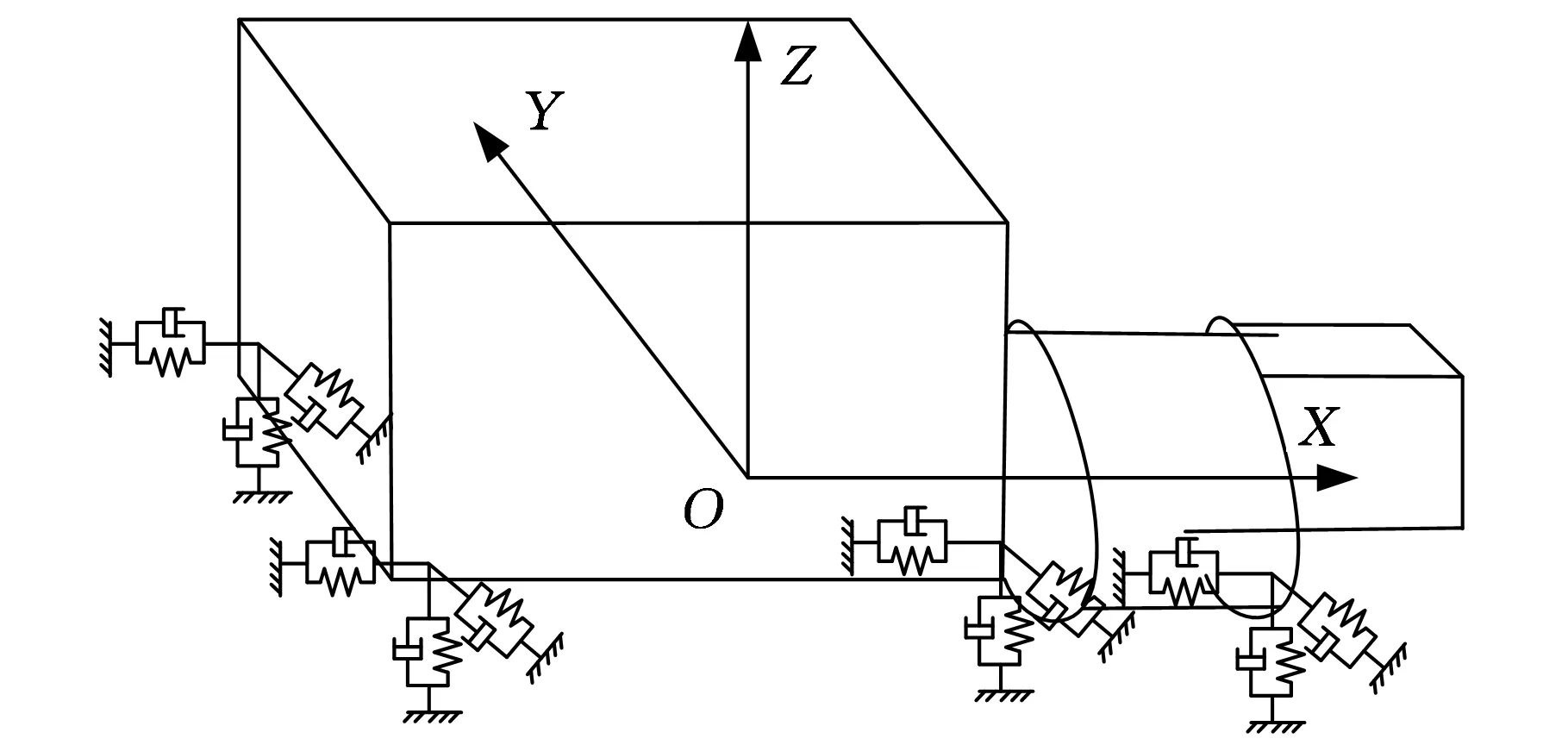
图1　动力总成悬置系统动力学模型

考虑到悬置的阻尼较小且对系统的动态特性和固有频率影响很小,故悬置的阻尼可以忽略不计。因此,对系统进行固有频率和固有振型的计算时,只需考虑无阻尼自由振动情况[3]。根据系统动力学知识,悬置系统的微分方程可以简化为无阻尼系统微分方程：

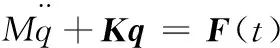
(2)

式中,M为系统的质量矩阵;K为系统的刚度矩阵;F(t)为系统所受的激振力。

1.2能量解耦法

多自由度振动系统中,耦合振动一直是限制悬置系统减振和隔振的最大障碍之一。能量解耦法可从能量角度实现各自由度的解耦,从而避免耦合振动。当系统以第i阶模态振动时,定义能量分布矩阵的第l行第j列分量为

(3)

l,j,i=1,2,…,6

式中,φl i、φj i分别为第i阶振型的第l个和第j个元素;Ml i为系统质量矩阵的第l行、第j列元素;ωi为第i阶固有频率。

第l个广义坐标分配的能量占系统总能量的百分比为

(4)

Pi l=100%时,系统作第i阶模态振动时的能量全部集中在第l个广义坐标上,此时,该阶模态完全解耦。

2　车内振动传递路径分析

2.1简化的传递路径分析模型

传递路径的分析技术在许多文献中均有介绍,这里不再详细阐述,在进行传递路径分析时,一般假设系统是线性非时变系统。动力总成作为单独的激励源，在其激励作用下振动沿悬置形成多条传递路径，并沿每条传递路径将振动能量传递至车内。车内目标位置的响应则是所有路径上产生的贡献量的线性叠加[4-6]:

(5)

式中,yk(ω)为目标点k的总贡献量;ω为频率;n、p分别为振动和声学传递路径的数量;Fi(ω)、Qj(ω)分别为作用在耦合被动端的结构载荷和声学载荷;Hk i(ω)、Hk j(ω)分别为耦合被动端与响应点之间的结构和声学频率响应函数。

在室内定置匀加速工况(800～2750 r/min)下,实测某型卡车动力总成悬置系统耦合主被动端以及车内目标点的振动响应。本试验选择5个考察目标：转向盘12点钟位置、主副驾驶员座椅导轨、仪表板中控台以及车辆顶棚，每个目标考察3个方向，共15个振动响应。同时计算各个路径的传递函数，建立动力总成到车内的振动传递路径分析模型。由于实验中激励源仅为动力总成，因此可将分析模型分为动力总成悬置子系统和车身结构子系统[7-8]。振动传递路径如图2所示。

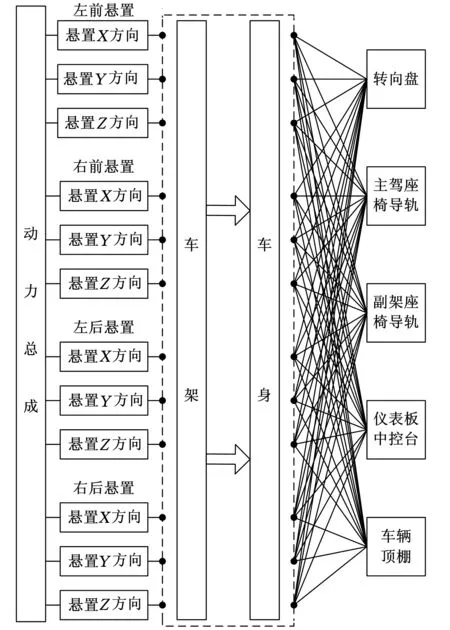
图2　振动传递路径示意图

将车内结构振动传递函数由动力总成悬置传递函数、车身加速度阻抗和车身结构传递函数来表示：

(6)

式中,k=1，2，3，4分别代表悬置1～4;Hmk为动力总成悬置传递函数;Zk为车身加速度阻抗;Hbk为车身结构传递函数;ae k为悬置耦合主动端振动加速度;abk为耦合被动端振动加速度;Fb k为力锤作用在耦合被动端测试点上的力;aok为目标点的振动加速度。

这样,车内结构振动传递函数即可简化为悬置子系统结构传递函数和车身结构子系统传递函数的乘积。该简化变换省去了拆卸动力总成并用力锤激励来测量车身响应这一繁琐过程,同时将每条传递路径用2个子系统传递函数表示[8]。

将利用此模型得到的车内目标点的加权振动作为振动目标函数，这样车内振动能够很好地得到描述。基于对上述两种方法的研究，认为将两者进行综合考虑可取得较好的效果。

2.2模型验证

在整车定置匀加速工况下，连续采集6组数据,然后拆除发动机，用力锤激励耦合被动端，测量车内目标点振动加速度，获取试验频响函数,现场测试情况如图3所示。对获取的工况数据和频响数据进行传递路径分析(transfer path analysis,TPA)处理,得到各路径每个工况下的贡献量数据以及各路径合成数据。

图3　TPA现场测试图

根据上述理论,在MATLAB环境下编写传递路径分析程序,读入6组试验数据,计算各路径的传递函数以及贡献量，进而建立整车振动传递路径分析模型。将转向盘12点钟位置垂向振动的实测数据与上述传递路径分析模型得到的合成振动数据对比,如图4所示。由图4可知,传递路径模型得到的合成振动幅值比实测值要小，这主要是因为传递路径分析模型未考虑实际整车与动力总成相连接的一些零部件对车内振动的贡献，但从整体上来说，合成振动趋势与实测情况相一致，验证了简化的传递路径分析模型的正确性和可靠性。

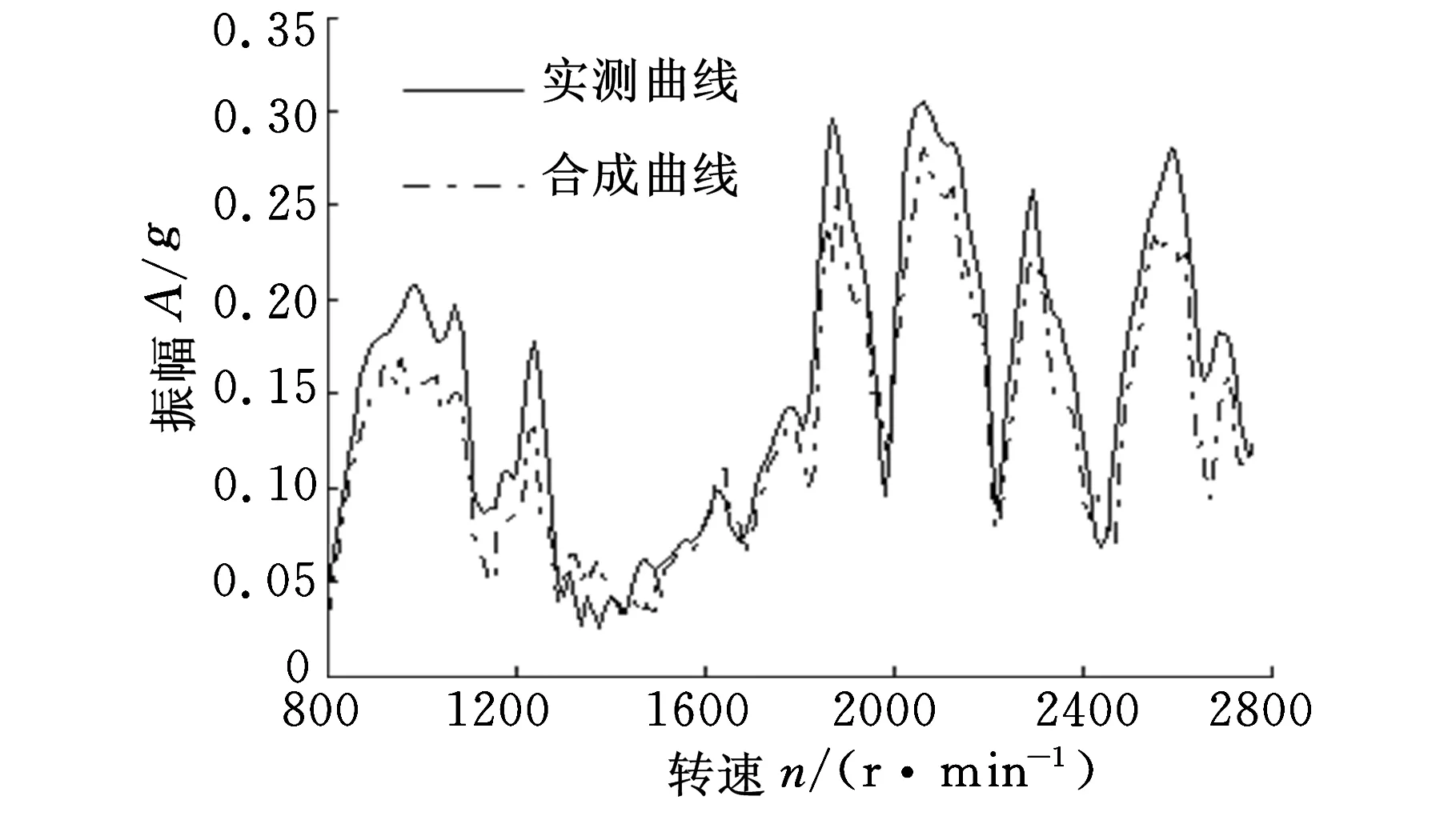
图4　转向盘垂向实测振动与合成振动对比

3　基于灰色粒子群算法的优化模型

3.1粒子群优化算法

粒子群优化(particle swarm optimization,PSO)算法和遗传算法相似,是进化算法的一种。PSO算法首先在解空间内随机初始化鸟群。鸟群中的每一只鸟称为“粒子”，这些“粒子”在解空间内以某种规律移动，经过若干次迭代后找到最优解[9]。迭代过程中,粒子通过跟踪2个极值不断调整自己的位置。一个极值是粒子本身所找到的最优解,被称为个体极值;另一个极值是整个种群目前所找到的最优解,称为全局极值。实际操作过程中,通过目标函数为每个粒子确定一个适应值来评价粒子的优劣程度。每个粒子都通过上述2个极值不断更新自己,从而产生新一代群体。

如果粒子的群体规模为m,则第i个粒子的位置Xi=[xi1xi2…xin],其速度Vi=[vi1vi2…vin],它的个体极值Pi=[pi1pi2…pi],种群的全局极值Pg=[xg1xg2…xg n]。粒子根据如下的公式来更新自己的速度和位置:

vid(t+1)=wvid(t)+c1r(pid(t)-

xid(t))+c2r(pg d(t)-xid(t))

(7)

xid(t+1)=xid(t)+vid(t+1)

(8)

d=1，2,…,n;i=1,2,…,m

式中,w为惯性权重因子;vi d为粒子的速度;pi d为局部最优解;pg d为全局最优解;r为0～1之间的随机数;c1、c2为学习因子,通常取c1=c2=2。

式(7)由三部分组成。第一部分表示粒子当前的状态,是粒子惯性的表现,体现了平衡全局和局部搜索的能力。搜索初期,较大的w有利于跳出局部极小点;搜索后期,较小的w有利于算法收敛。第二部分是个体认知部分,这部分使粒子具有较强的全局搜索能力,避免陷入局部极小。第三部分是社会认知部分,这部分使粒子从其他优秀粒子中汲取经验,提升粒子全局搜索能力[10]。

3.2灰色粒子群优化算法

多目标优化问题和单目标优化问题有着本质的区别,前者一般是一组或几组连续解的集合,后者是单个解或一组连续解的集合[11]。粒子群算法不能直接应用于多目标问题求解过程中,但将灰色关联度引入粒子群算法中对最优解进行评估可以实现多目标问题的优化。

设基准矢量序列Y0={y0(j)}(j=1,2,…,p),目标矢量序列Yi={yi(j)}(i=1,2,…,m);m为目标矢量个数。则Yi对于Y0在j点的灰色关联系数为

ε0i(j)=

(9)

灰色关联度为

(10)

式中,ζ为分辨系数,取值在0～1之间,通常取ζ=0.5。

3.3优化设计

3.3.1设计变量

由于实际限制,一般动力总成本身物理参数如质量、惯量等通常难以改变,支承位置和安装角度受到其他器件和空间的限制,也很难改变。所以只以4个悬置元件的u向、v向、w向的刚度k=(kiu,kiv,kiw)(其中i=1，2，3，4)为设计变量,故共有12个设计变量。

3.3.2目标函数

(1)能量解耦。根据式(4)可知,系统在作某阶固有频率振动时,振动占优方向所占的振动能量百分比Pi l其值越大,系统解耦程度越高[12]。因此系统的能量解耦目标函数可确定为

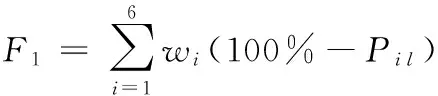
(11)

式中,wi为第i阶频率的加权因子。

考虑到发动机的激励主要集中在垂直方向和绕曲轴旋转方向上,因此优化过程中将这两个方向的加权因子都取为5,其余取1。

(2)车内振动。根据优化前车内目标点振动情况，将工况下整个转速范围分为3个部分,每部分给予不同的加权因子，将车内所有目标点各方向振动平均水平综合在一起考虑，确定目标函数为

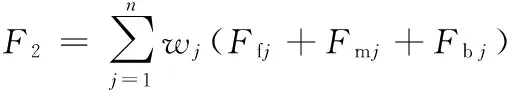
(12)

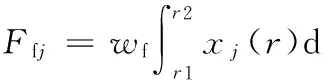
式中,r1、r2、r3、r4为车辆定置升速过程中所对应的转速,r1=800 r/min,r2=1400 r/min，r3=1950 r/min，r4=2750 r/min;wj为对应于车内第j个目标点的加权因子。

考虑到车内驾乘人员对转向盘和座椅导轨振动主观感受明显,优化过程中将车内转向盘、主副驾座椅导轨这3个考察目标点的加权因子取为5,其余目标点取为2。结合优化前实测目标点振动情况，将转速范围的前一段加权因子wf取为3,中间一段加权因子wm取为2,后一段加权因子wb取为4。

3.3.3约束条件

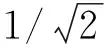
3.4算法运行参数

具体优化过程中取种群大小10,粒子大小12,目标函数个数2,最大迭代次数nmax=60,学习因子c1=c2=2,最大粒子速度vmax=5。惯性权重因子w的最大值wmax=0.9,最小值wmin=0.4,迭代计算过程中w(t)=wmax-(wmax-wmin)t/nmax。

3.5算法流程

将灰色关联度引入粒子群算法中,具体优化流程图如图5所示。

(1)初始化粒子种群:给定种群规模m、学习因子c1、c2、惯性权重因子w、目标函数的个数和最大迭代次数。

(2)根据约束条件随机产生10个粒子的位置和速度。

(3)利用粒子群算法分别求出两个子目标函数的最优解,然后组成基准矢量序列。

(4)将粒子群位置代入目标函数,计算出目标函数值,将目标函数值组成目标矢量序列。

(5)利用式(9)、式(10)求出每个粒子形成的目标矢量的关联度,比较关联度的大小,将种群中关联度最大的作为全局极值,粒子飞行中最大关联度的作为个体极值。

(6)利用式(7)、式(8)更新粒子位置。

(7)返回第(4)步进行循环迭代计算60次。

(8)记录全局极值粒子对应的最优变量和最优值。

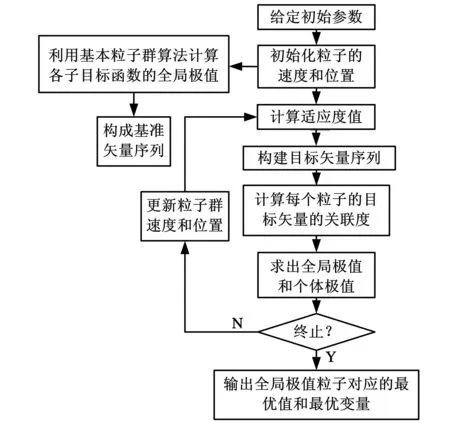
图5　优化流程图

4　实例与优化

某型卡车的发动机为四缸四冲程发动机,发动机悬置方式为四点斜置(前悬置倾斜角度为48°,后悬置倾斜角度为18°,4个悬置元件左右对称布置,左前悬置坐标(单位mm,下同)为(62.7,-291.0,-194.0),右前悬置坐标为(62.7,291.0,-194.0),左后悬置坐标为(1196.0,-306.0,-326.0),右后悬置坐标为(1196.0,306.0,-326.0),发动机总质量为565.6 kg,质心坐标为(549.6,-2.3,-115.7)。表1所示为发动机动力总成的质量和惯量参数,表2所示为悬置系统的刚度参数。

表1　发动机总成惯量参数　kg·m2

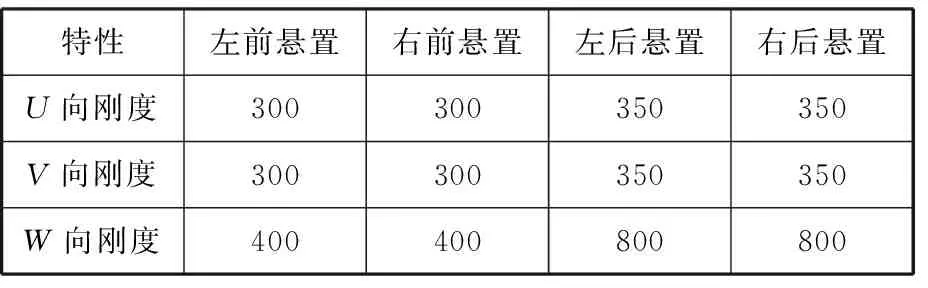
表2　悬置系统刚度参数　N/mm

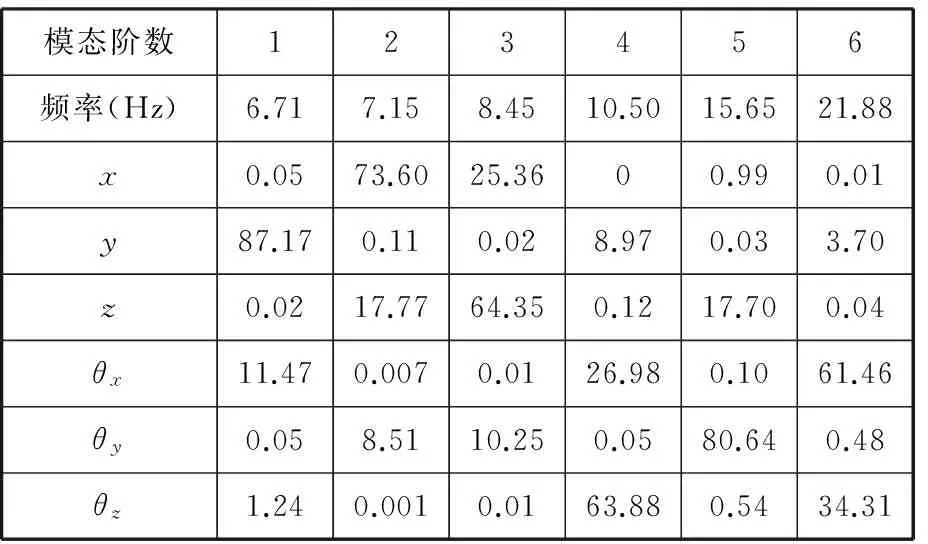
表3　系统振动耦合的能量分布百分比　%

从表3可以看出,悬置系统的前6阶固有频率满足频率分布要求,但最高固有频率为21.88 Hz,大于18.86 Hz,不满足频率分布要求,隔振效果不理想,同时悬置系统除了Y向和绕Y轴的两个自由度上的能量分布大于75%外,其他自由度上的能量分布均小于75%,尤其是重要指标方向——Z向自由度和绕X轴的自由度(θX)上的能量分布分别只有64.35%和61.46%,明显低于解耦率指标要求,耦合情况严重,需要改进。

利用灰色粒子群多目标优化策略,在MATLAB环境下编写优化程序,最终优化获得针对悬置12个主轴刚度变量的优化结果(表4)，此时，系统振动解耦情况如表5所示。

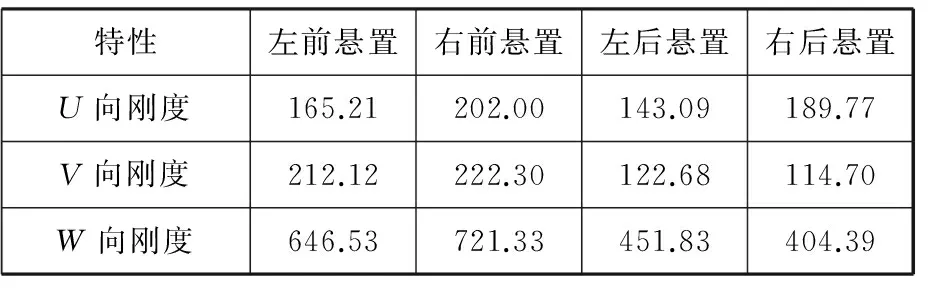
表4　优化后各悬置刚度参数　N/mm

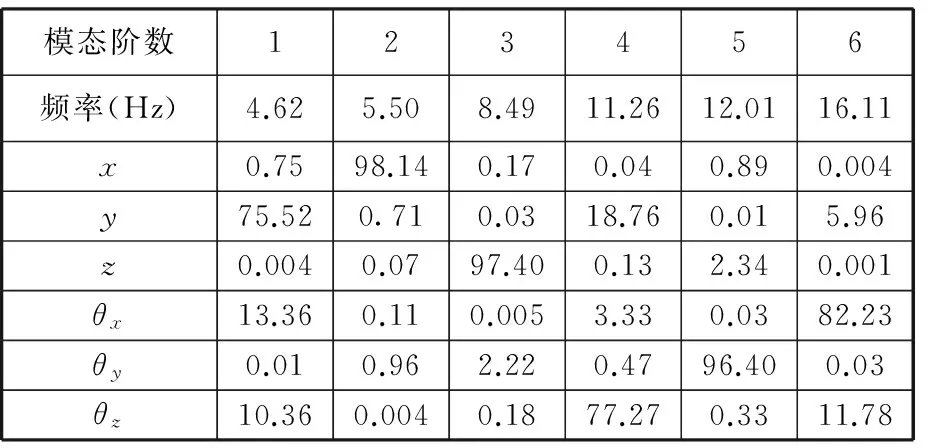
表5　优化后系统振动耦合的能量分布百分比　%

对比表3与表5可以看出,优化后的频率分布在4.62～16.11 Hz之间,满足频率分布要求,且各频率间的间隔也大于0.5 Hz,满足实际要求。最大固有频率比优化前有大幅度降低,共振频率带宽减了小30%,频率配置更加合理。除了Y向自由度上的能量分布比优化前有所降低,其他自由度上的能量百分比都有大幅提高,主要的Z向自由度上的能量百分比由64.35%提高到97.40%,绕X轴的自由度上的能量百分比由61.46%提高到82.23%。优化后,整个悬置系统的振动耦合得到降低。

对于上述优化后的悬置系统,用蒙特卡洛法进行分析,以确定悬置刚度对振动耦合能量分布的影响。设置各个刚度变量的数目为1000,并假定悬置的刚度值在±15%的范围内变化,且满足正态分布。图6、图7所示分别为Z向和绕X轴的解耦度的蒙特卡洛法分析结果。

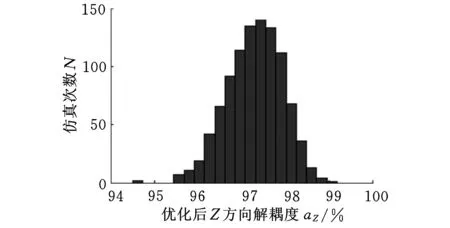
图6　优化后Z向解耦度分布概率

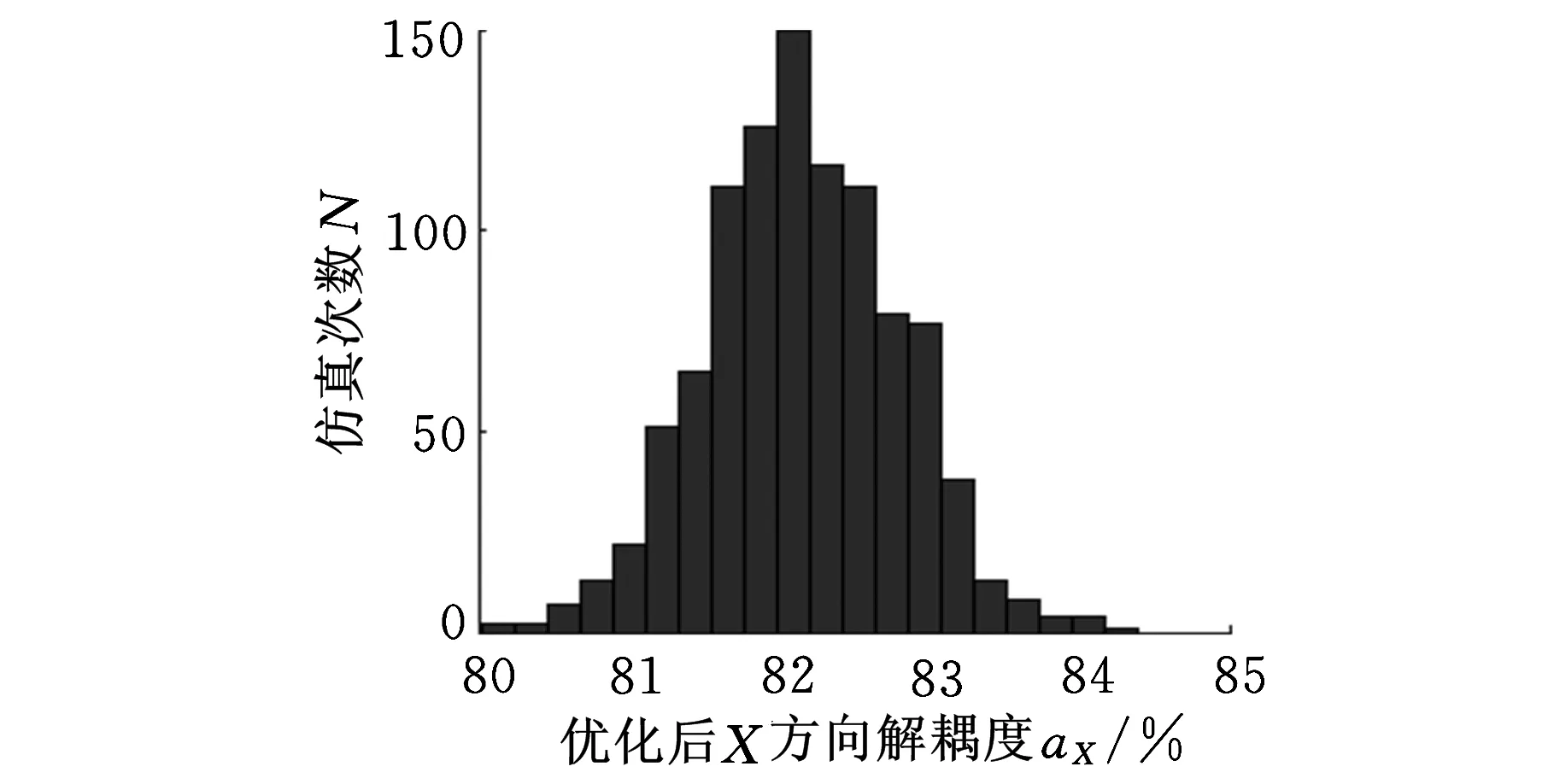
图7　优化后绕X向解耦度分布概率

从图6、图7可知,优化后的Z向和绕X向的解耦度分布情况都较为合理,最高与最低差值只有4%,优化结果具有较高的稳健性。

5　实验验证

5.1模态频率验证

利用锤击模态测试法对优化后的动力总成悬置系统进行刚体模态测试,获得6阶模态参数。现场测试场景如图8所示。主要的Z向平动和绕X轴转动的振型,如图9、图10所示。将实测得刚体模态频率与优化得到的频率进行比较,见表6。

图8　刚体模态测试图

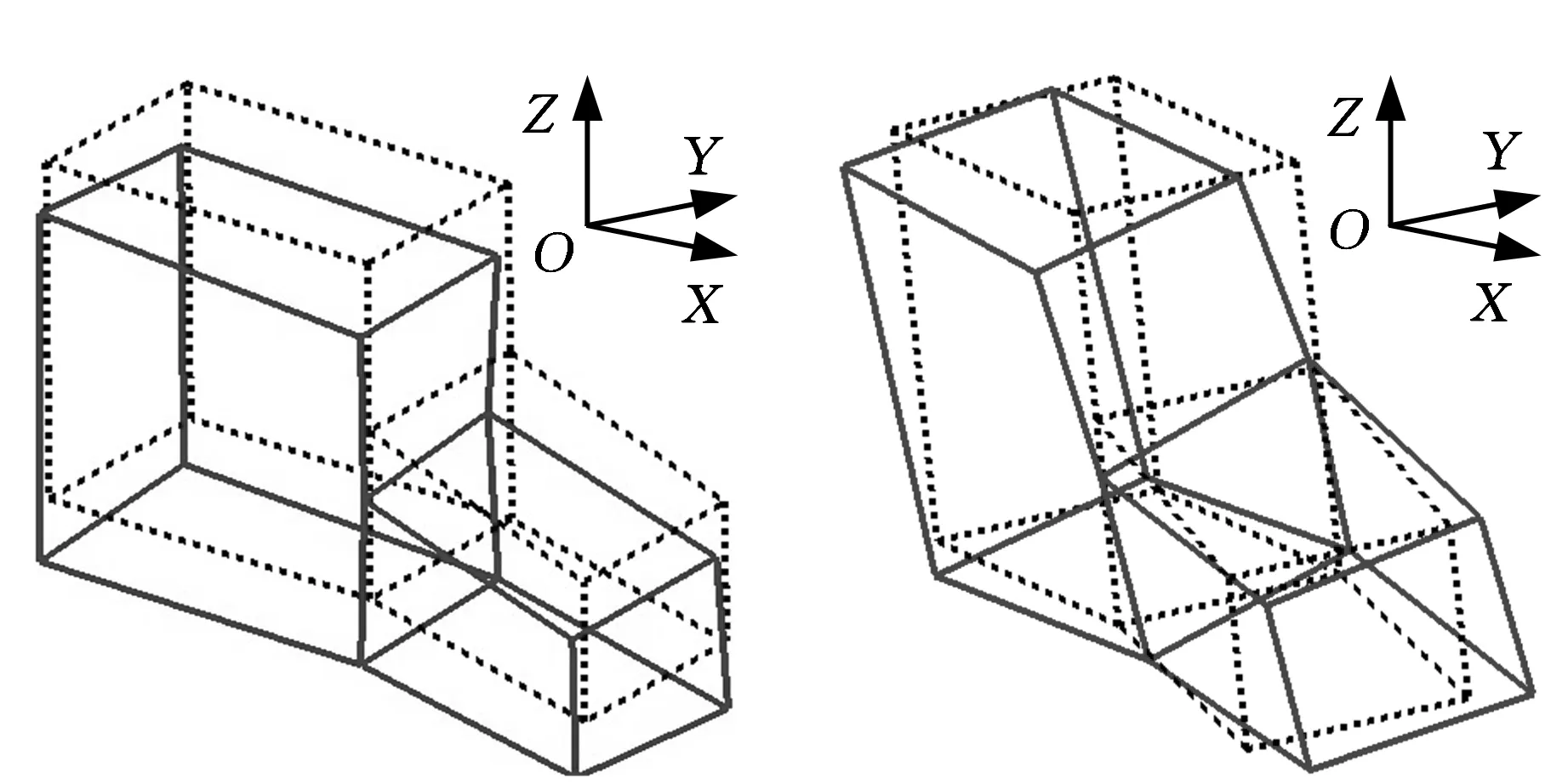
图9　沿Z向平动振型图10　绕X轴转动振型

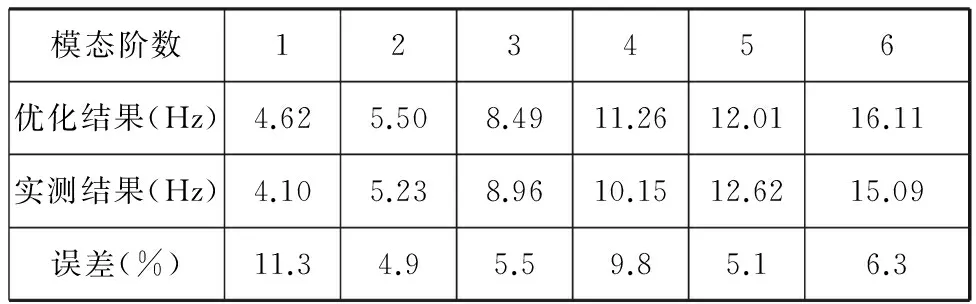
模态阶数123456优化结果(Hz)4.625.508.4911.2612.0116.11实测结果(Hz)4.105.238.9610.1512.6215.09误差(%)11.34.95.59.85.16.3

由表6可以看出,实测得到的模态频率分布合理,也满足隔振要求,并且与优化结果最大误差只有11.3%。造成这些误差的原因主要有两个:一方面是实测环境复杂,存在外部干扰因素;另一方面悬置刚度在实际生产中会存在一定波动。总体上来说,实测得到的刚体模态与优化得到的模态频率基本一致,验证了优化方法的正确性。

5.2车内振动验证

对优化后的整车进行车内振动测试，将测试结果与优化前的车内振动进行对比，如图11～图13所示。

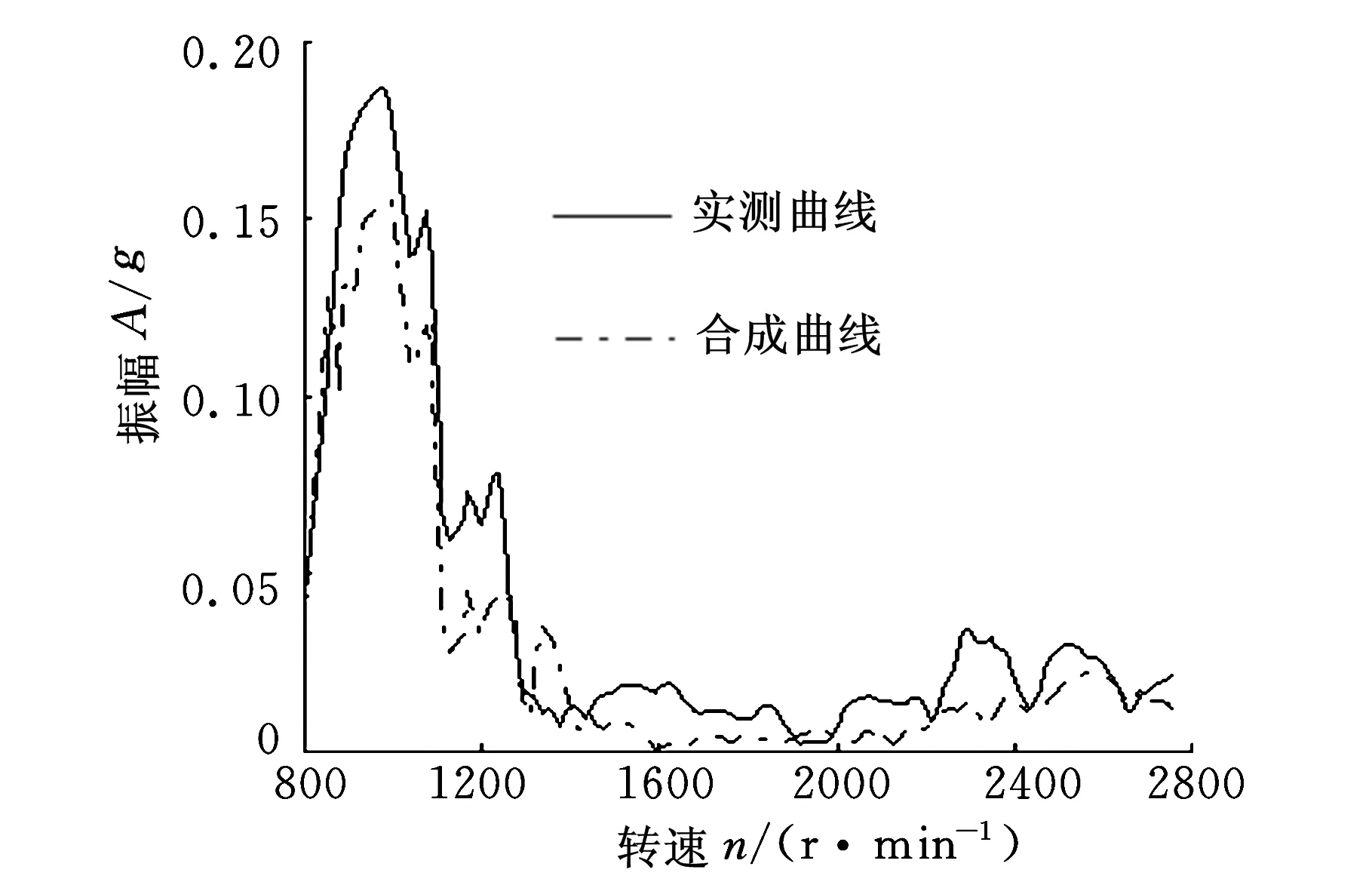
图11　转向盘X向振动

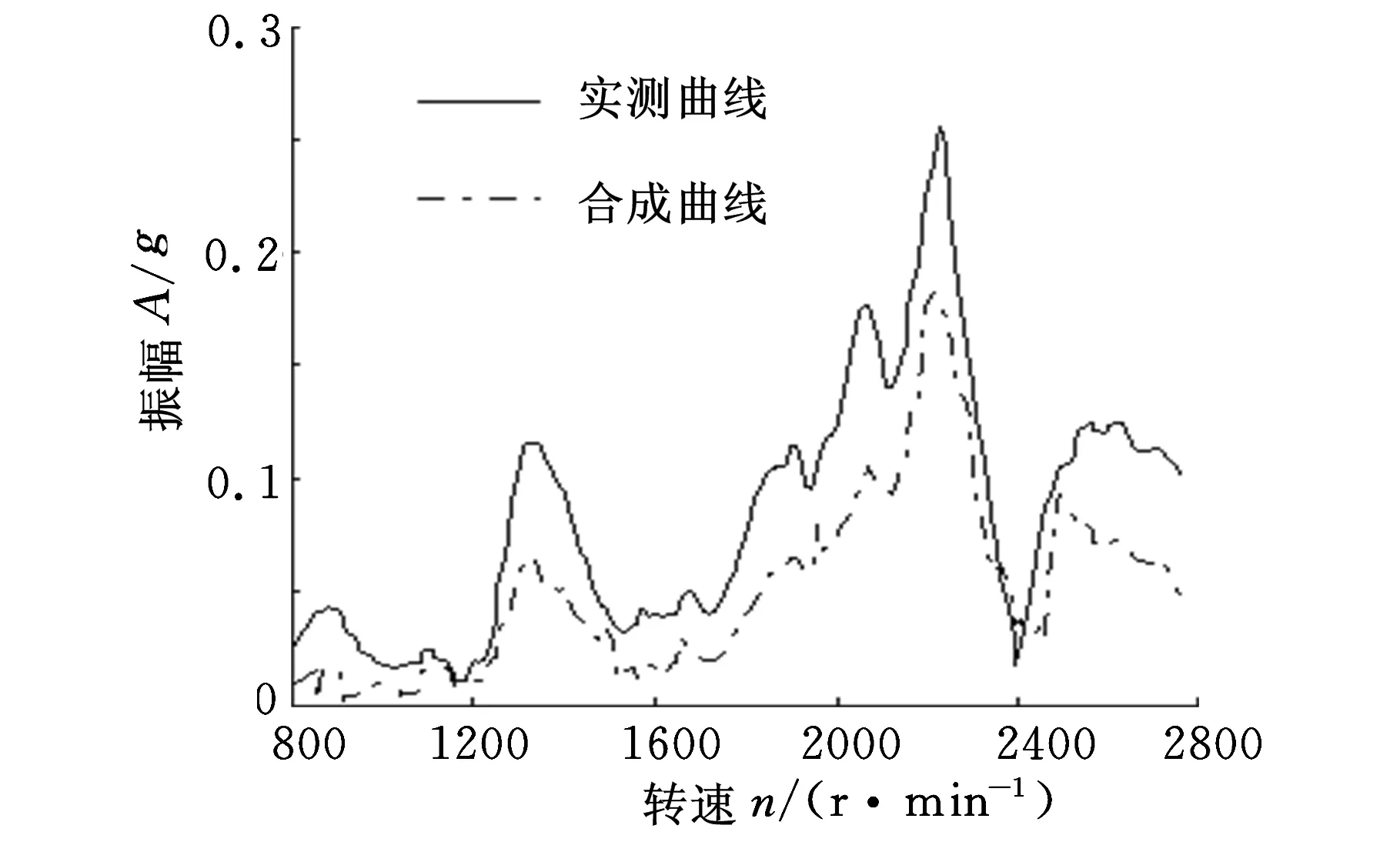
图12　主驾座椅导轨Z向振动

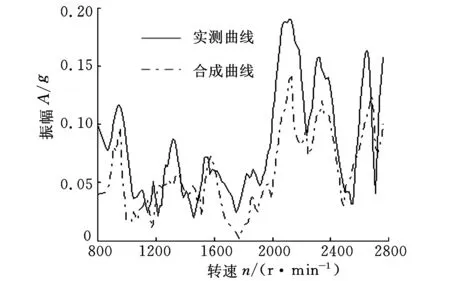
图13　副驾座椅导轨Y向振动

从图11～图13可以看出,虽然优化后个别频率下的振动比优化前稍大,但车内所有考察目标点的整体振动水平较优化前都有大幅降低,验证了本文优化模型的有效性。

6　结论

(1)为了有效描述车内振动，建立了基于实验数据的简化传递路径分析模型。将整车传递路径系统简化为动力总成悬置子系统和车身结构子系统,并进行了实验验证。

(2)综合考虑能量解耦和车内振动，建立了基于灰色粒子群优化算法的多目标优化模型。优化结果表明，该方法不仅较好地实现了悬置系统能量解耦，而且降低了车内振动，避免了动力总成悬置系统优化设计目标的单一性和局限性，为动力总成悬置系统的优化设计提供了新的思路和有价值的参考。

[1]TamboliJA,JoshiSG.OptimumDesignofaPassiveSuspensionSystemofaVehicleSubjectedtoActualRandomRoadExcitations[J].JournalofSoundandVibration,1999,219(2):193-205.

[2]吴飞,胡朝辉,成艾国,等.综合考虑解耦率和隔振率的发动机悬置系统多目标优化[J].汽车工程,2013,35(1):18-22.

WuFei,HuChaohui,ChengAiguo,etal.TheMulti-objectiveOptimizationofEngineMountSystemConcurrentlyConsideringEnergyDecouplingRateandVibrationIsolationRate[J].AutomotiveEngineering,2013,35(1):18-22.

[3]张武,陈剑,夏海.基于灵敏度分析的发动机悬置系统稳健优化设计[J].汽车工程,2009,31(8):728-732.

ZhangWu,ChenJian,XiaHai.RobustOptimalDesignofanEngineMountingSystemBasedonSensitivityAnalysis[J].AutomotiveEngineering,2009,31(8):728-732.

[4]LiWei,WangDengfeng,ChenShuming,etal.TransferPathAnalysisofPowertrainVibrationonDriver’sNoise[C]//2011SeventhInternationalConferenceonNaturalComputation.Shanghai,2011:2353-2357.

[5]JanssensK,GajdatsyP,GielenL,etal.OPAX:ANewTransferPathAnalysisMethodBasedonParametricLoadModels[J].MechanicalSystemsandSignalProcessing,2011,25(4):1321-1338.

[6]李未,李庆华.动力总成振动对车内噪声的传递路径影响[J].智能系统学报,2012,7(2):183-187.

LiWei,LiQinghua.TransferPathAnalysisofPowerTrainVibrationonAutomotiveInteriorNoise[J].CAAITransactionsonIntelligentSystems,2012,7(2):183-187.

[7]龙岩,史文库,蒋凌山,等.动力总成悬置系统优化方法的对比研究[J].汽车工程,2011,33(10):875-879.

LongYan,ShiWenku,JiangLingshan,etal.AComparativeStudyontheOptimizationMethodsforPowertrainMountingSystem[J].AutomotiveEngineering,2011,33(10):875-879.

[8]龙岩,史文库,梁天也,等.基于改进传递路径分析法的动力总成悬置系统优化及评价[J].汽车工程,2009,31(10):957-962.

LongYan,ShiWenku,LiangTianye,etal.OptimizationandEvaluationofPowertrainMountingSystemBasedonImprovedTransferPathAnalysisTechnique[J].AutomotiveEngineering,2009,31(10):957-962.

[9]PoliR,KennedyJ,BlackwellT.ParticleSwarmOptimization[J].SwarmIntelligence,2007,1(1):33-57.

[10]张武,陈剑,高煜.基于粒子群算法的发动机悬置系统稳健优化设计[J].农业机械学报,2010,41(5):30-35.

ZhangWu,ChenJian,GaoYu.RobustOptimalDesignofanEngineMountingSystemBasedonParticleSwarmOptimization[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2010,41(5):30-35.

[11]于繁华,刘仁云.计算智能技术及其工程应用[M].北京:科学出版社,2010.

[12]时培成,陈无畏,高立新.基于蒙特卡罗法的动力总成悬置系统稳健性设计[J].汽车工程,2010,32(8):707-711.

ShiPeicheng,ChenWuwei,GaoLixin.RobustnessDesignofPowertrainMountSystemBasedonMonteCarloMethod[J].AutomotiveEngineering,2010,32(8):707-711.

(编辑张洋)

Multi-objective Optimization of Powertrain Mount System Concurrently Considering Energy Decoupling and Vehicle Vibration

Chen JianShi WeiyiJiang FengxinZeng WeijunShen ZhongliangWang Yifeng

Hefei University of Technology,Hefei,230009

Simplified vehicle vibration TPA model was established based on the actual transfer path test datum.On the basis of that,multi-objective optimization model of powertrain mount system was established based on GPSO algorithm with considering energy decoupling and vehicle vibration,mounting stiffness parameters were taken as design variables.Taking a truck for example, a multi-objective optimization solution was conducted.The test and optimization results show that the optimization method can get better energy decoupling and lower vehicle vibration,while achieving the optimal matching of energy decoupling and cars and low vibration.

powertrain mounting system;transfer path analysis(TPA);grey particle swarm optimization(GPSO);Monte Carlo method

2014-04-16

U463.33DOI：10.3969/j.issn.1004-132X.2015.08.024

陈剑,男,1962年生。合肥工业大学噪声振动工程研究所教授、博士研究生导师。主要研究方向为汽车NVH与CAE、机器低噪声设计、声质量设计。发表论文50余篇。史韦意,男,1989年生。合肥工业大学噪声振动工程研究所硕士研究生。蒋丰鑫,男,1987年生。合肥工业大学噪声振动工程研究所硕士研究生。曾维俊,男,1989年生。合肥工业大学噪声振动工程研究所硕士研究生。沈忠亮,男,1989年生。合肥工业大学噪声振动工程研究所硕士研究生。汪一峰,男,1990年生。合肥工业大学噪声振动工程研究所硕士研究生。