基于改进豪斯多夫距离的非参数轮廓变点识别
2015-10-28孙会东杜文超
聂 斌 孙会东 李 佩 杜文超
天津大学,天津,300072
基于改进豪斯多夫距离的非参数轮廓变点识别
聂斌孙会东李佩杜文超
天津大学,天津,300072
轮廓监控中的变点识别问题是统计过程控制的重要研究内容。以非参数轮廓数据为研究对象,运用图像特征识别的豪斯多夫距离测量了样本轮廓之间的特征差异,设计了改进方法,提出了基于二维空间的改进豪斯多夫距离算法,以识别非参数轮廓变点。大量的仿真与论证表明,改进方法在识别变点位置和稳定性方面具有优异的性能。
非参数轮廓;变点识别;豪斯多夫距离;T2统计量
0 引言
在工业生产中,质量控制是统计质量管理的重要工具。统计过程控制(statistical process control,SPC)即应用统计方法对生产过程进行监控,可以通过分析工具直观地观察到过程中发生的异常波动。随着科学技术的发展,产品的质量特征从单一性逐渐过渡到多样性,质量监控也发展为需测量一系列产品特征参数,以便对产品质量进行更出色的监控。近年来,轮廓监控已成为学者们研究的热点。
所谓“轮廓”即为描述产品质量特性的函数关系,其响应参数对应一个或多个产品解释变量。轮廓监控方法是将控制图理论与其他数据分析技术相结合,对以质量特性为轮廓的产品进行质量监控的方法,如锻件锻压力、半导体制造中晶体腔体和发动机叶片等轮廓监控问题。Hawkins等[1]提出,轮廓监控包含两个阶段:在阶段一(Phase Ⅰ),通过对历史样本数据的分析,判断失控样本点并移除,从而确立受控的轮廓参数;在阶段二(Phase Ⅱ),通过Phase I确定的受控状态的产品轮廓参数,时时动态检验未来数据受控与否。
在现阶段的研究中,简单线性轮廓的监测问题已经相对成熟[2-4]。然而,在工程应用和理论研究方面,往往面对的是非线性轮廓的问题,如Ding等[5]提到的锻压力监控问题。与线性轮廓相比,非线性轮廓很难采用回归分析理论,非参数轮廓模型回归时则更加困难。在非线性轮廓回归分析中,一些学者提出了自己的分析理论,如Williams等[6]和Zou等[7]分别提出了基于参数和非参数的非线性回归模型,Jensen等[8]提出了基于T2的非线性固定轮廓,Qiu等[9]提出了基于指数加权滑动平均(EWMA)的非参数固定效应模型分析方法,Chicken等[10]提出了半参数化的小波分析方法,邹长亮[11]提出了基于惩罚函数的多元统计监控问题,更加详细的描述请参考文献[12]。
近年来,通过非线性回归方法评估参数的做法已经具有相当程度的局限性,这使得避开回归分析采用其他轮廓监控技术进行分析得到愈加广泛的重视。以Ding等[5]为代表的众多学者提出通过主成分分析(principal component analysis,PCA)的方法对高维轮廓降维并提取轮廓样本数据之间的变异。Zhang等[13]提出了基于度量误差和在工件轮廓解释变量位置非固定的情况下,度量在容许公差值范围内的轮廓偏移值的方法。Shiau等[14]推荐采用HotellingT2控制图来监控非线性轮廓主成分得分。Williams等[15]引用了更为一般的非参数方法,即比较各轮廓与基准轮廓之间的差异性。Vaghefi等[16]提出了一种基于测量样本轮廓与假定受控轮廓之间的面积偏移绝对值的新方法。Zhang等[17]提出了通过构建χ2统计量来确定轮廓偏移标准的方法。
豪斯多夫距离算法是通过计算两组样本点之间的距离来度量样本间相似度的算法。作为一种有效而实用的算法,豪斯多夫距离算法近年来被众多学者广泛应用于图像识别与目标跟踪等模式识别领域。然而,豪斯多夫距离对噪声点、孤立点等特殊点的敏感性也增加了豪斯多夫距离在识别样本差异之间的偶然性。鉴于此,Dubuisson等[18]提出了样本维度间距离均值的修正豪斯多夫距离的算法。
针对非参数轮廓变点识别问题,本文提出一种基于二维空间的修正豪斯多夫算法(two dimensional modified Hausdorff distance,TD-MHD),并测定样本轮廓与基准轮廓之间的局部偏移,通过T2变点识别方法监控非参数轮廓的局部变异变点。
1 模型提出与假设
对于非线性轮廓,假设产品特征Y=(y1,y2,…,yp)为某些固定位置的独立变量X=(x1,x2,…,xp)的函数,即任意时刻的产品质量特性表现为Y与X的函数关系(轮廓),其中X代表测量范围内的取值点,Y代表其对应的质量特征值,则当处于统计受控状态时,存在以下关系:
yi j=f(xi j,βi j)+εi ji=1,2,…,m;j=1,2,…,p
(1)
其中,β为轮廓系数,误差项ε假定为独立同分布(i. id.)正态随机变量,服从N(μ,σ2)正态分布,m为轮廓的个数,p为每个轮廓取值点的个数。在本文中,为了便于研究,假设每次测量位置不变,即独立变量X对于任意样本均相同。那么对于每个观测的样本而言,研究对象为响应因子Y。对于m个样本(y11,y22,…,y1p),…,(ym1,ym2,…,ym p),每个样本均为p维二元矢量。
在本文中,假设原始样本数据识别为单变点识别。假设变点位置为τ,非线性轮廓模型式(1)表示为
(2)
1.1传统豪斯多夫距离(HD)
对于同一个空间内任意两个点集之间的相似程度,豪斯多夫距离在不需要点集之间一一对应关系情况下可以有效处理很多特征点的情况。对于历史样本集中任意两个独立样本yi=(yi1,yi2,…,yjp)和yj=(yj1,yj2,…,yjp),其中i,j=1,2,…,m且i≠j,则其豪斯多夫距离为
H(yi,yj)=max(h(yi,yj),h(yj,yi))
(3)
(4)
豪斯多夫距离可以在保留样本间差异的情况下将样本数据直接降到一维,大大减小了样本数据的复杂度。样本数据Y通过豪斯多夫距离降维得到:
DH=(H(y1,y2),H(y2,y3),…,H(ym-1,ym))
(5)
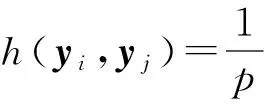
1.2基于二维空间的改进豪斯多夫距离
在传统的豪斯多夫距离概念中,求解任何两数组之间的距离首先需计算其中一组数组中任一数据到另一数组中所有数据的距离。然而,在轮廓等二维数据中,在计算上述距离时首先应考虑该轮廓数据各观察值的位置参数。因此,有必要将轮廓中各观察值的位置参数引入距离测定,且大量仿真实验亦表明了其必要性。在轮廓二维空间中,任意两个轮廓观测值(即两个轮廓yi,yj)之间的距离d为
d(yi,yj)=
(6)
依次设d(yi,yj)=(di1,di2,…,dip)T=(dj1,dj2,…,djp),则dik(djk)表示第i个(第j个)轮廓的第k个观测值与第j个(第i个)轮廓中第1,2,…,p个观测值距离的矢量。
样本轮廓yi j中存在随机误差项,在应用传统豪斯多夫距离情况下,误差项的波动直接导致轮廓点之间距离的随机波动放大,使得选取的最小点距离(式(4))随随机误差而振荡。为了消除随机误差产生的影响,本文采用求取两样本之间点距离中位数的平均值的方法来计算两个样本间的TD-MHD,计算公式如下:
(7)
(8)
则DT=(H′(y1,y2),H′(y2,y3),…,H′(ym-1,ym))即为求得样本轮廓间的豪斯多夫距离。
1.3χ2统计量方法
针对高维复杂轮廓的变异识别问题,Zhang等[17]提出基于χ2统计量的控制方法。在轮廓控制Phase I,针对一组样本轮廓数据,由于其参数的未知性,往往在构建统计量时需要采用一定的方法寻求均值和方差参数估计值。所提χ2统计量如下:
(9)
其中,μs、Σs分别表示样本轮廓的均值和协方差。由于在样本数据中可能已经存在变异点,因此,在如何评估均值和方差方面,本文提出基于中位数的均值和方差估计的方法。
(1)样本均值计算方法如下:
(10)
(11)
(2)样本协方差计算方法如下:
①在轮廓各维度固定情况下,依次计算两两对应样本(m(m-1)/2)中相同维度的数值差:
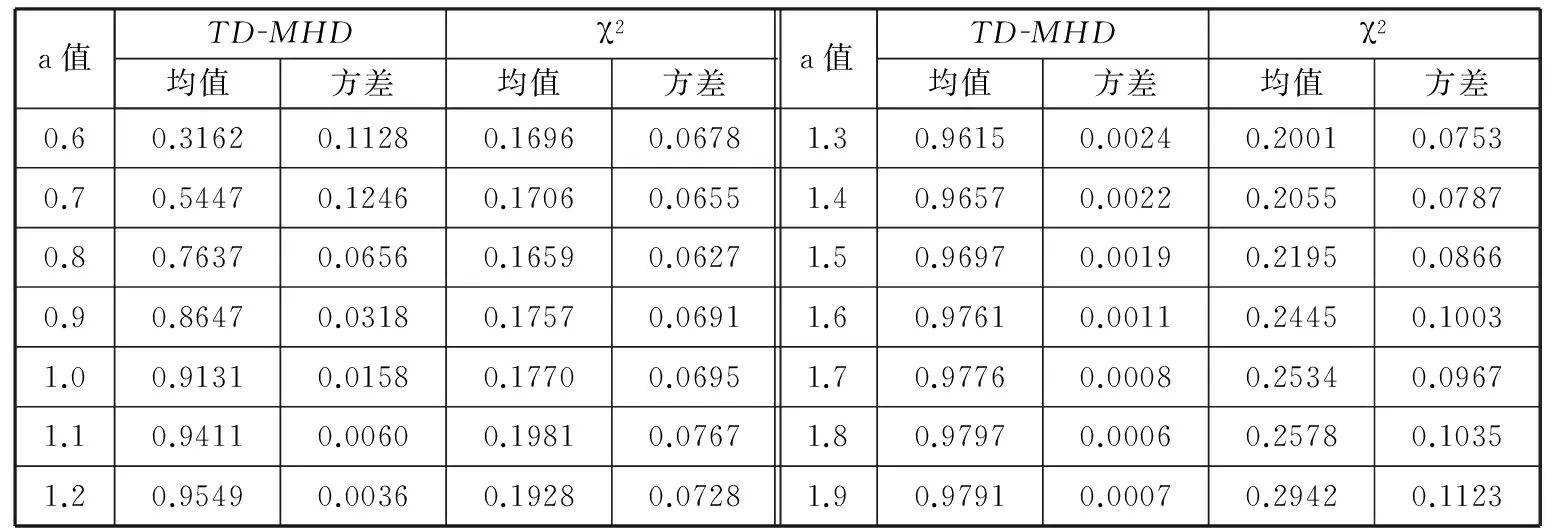
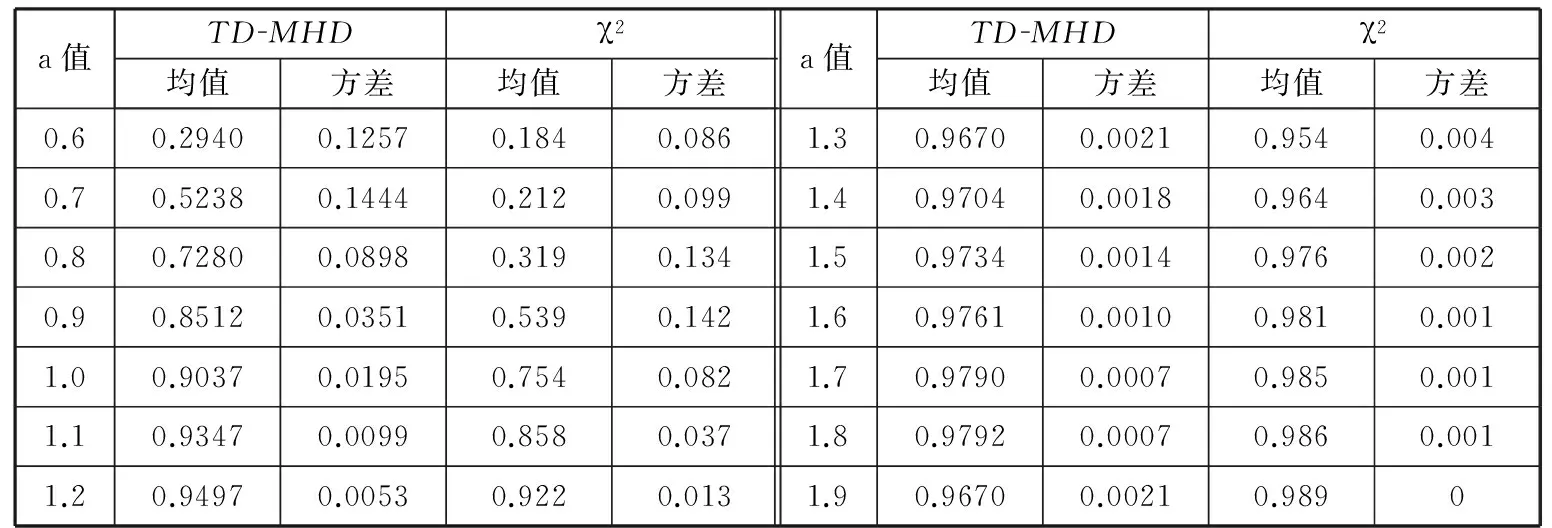
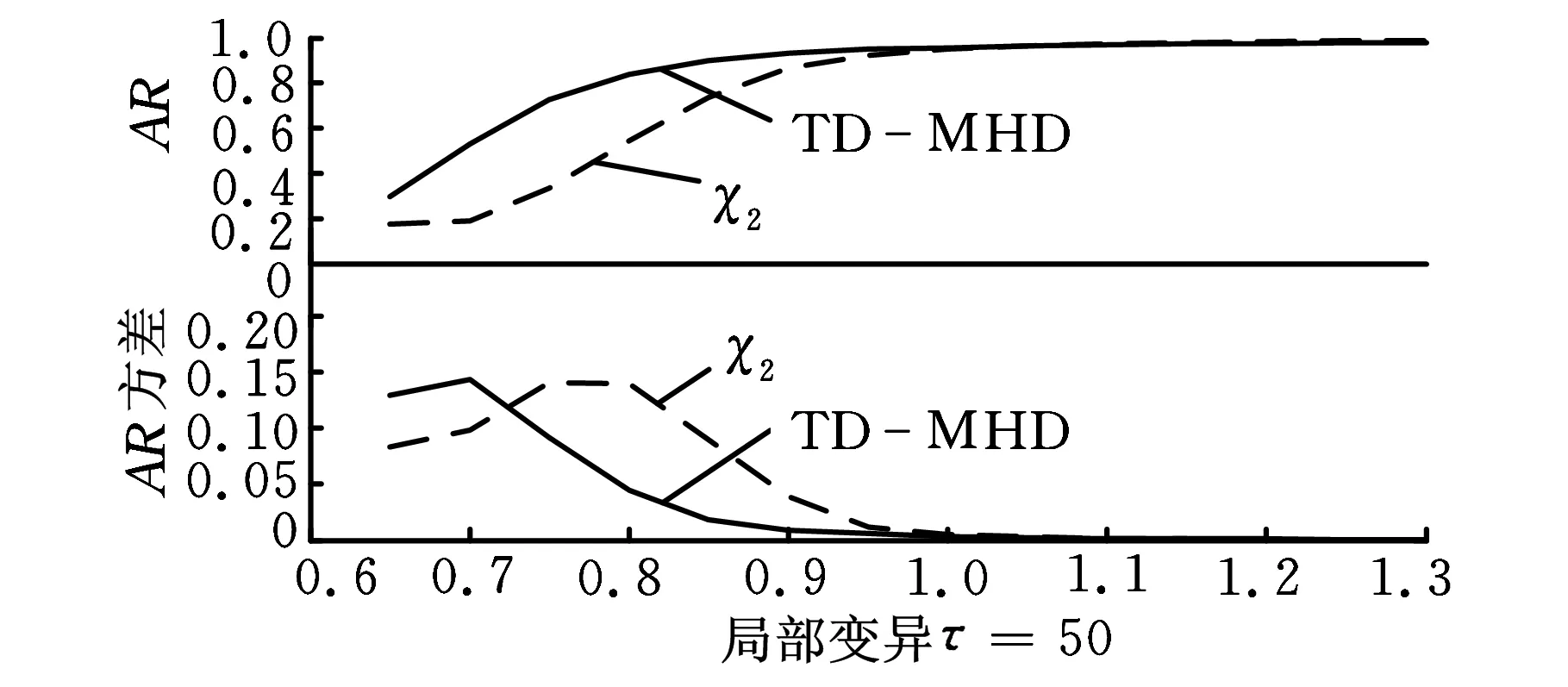
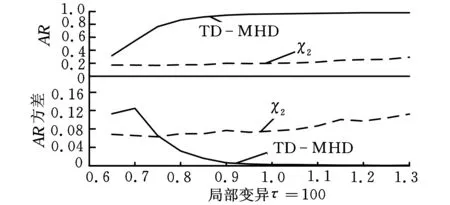
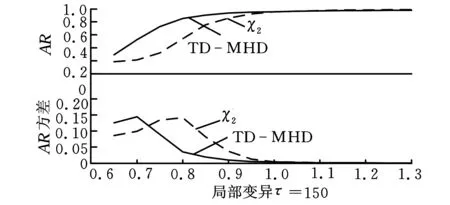
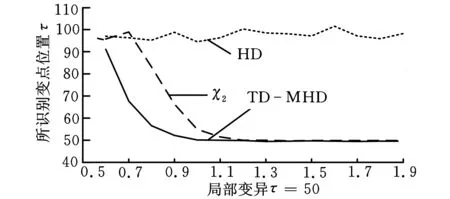
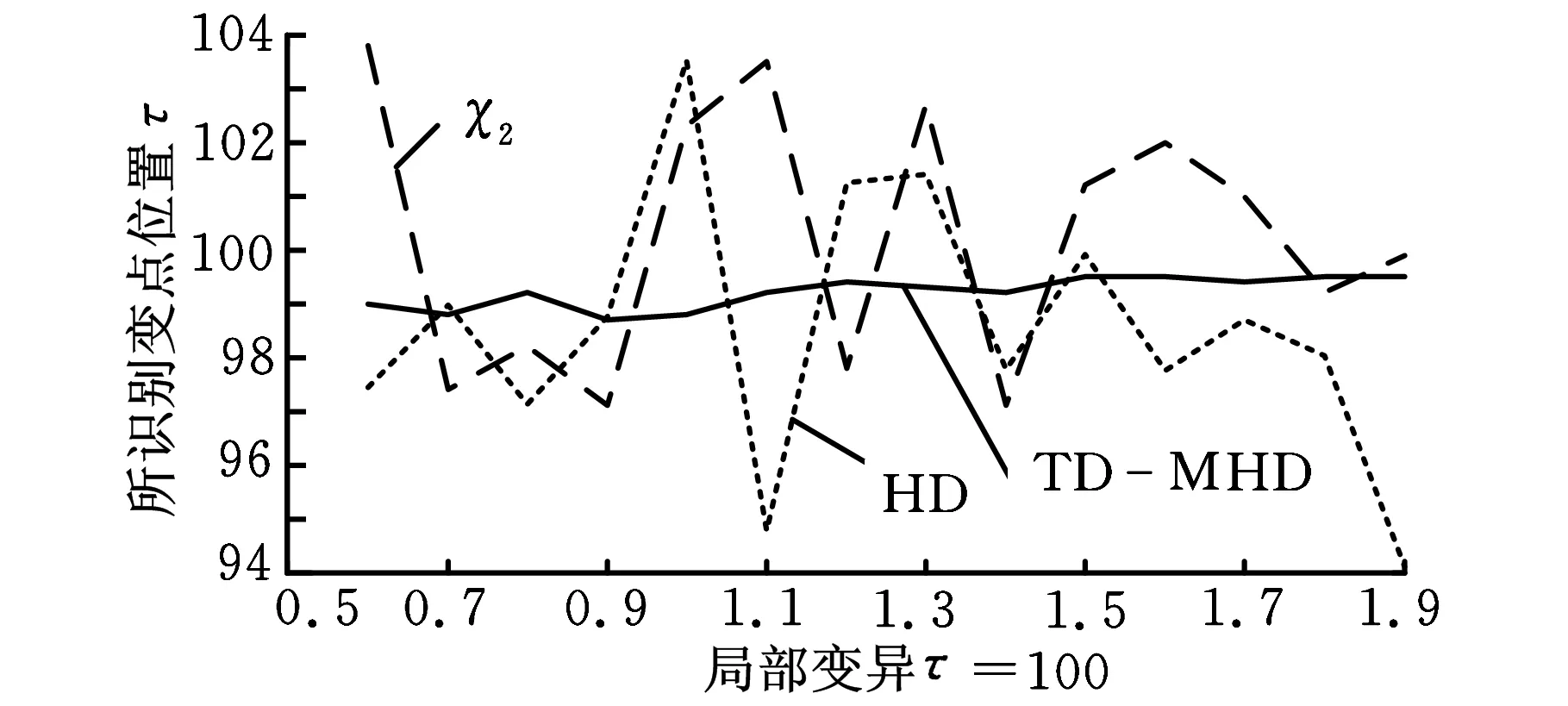
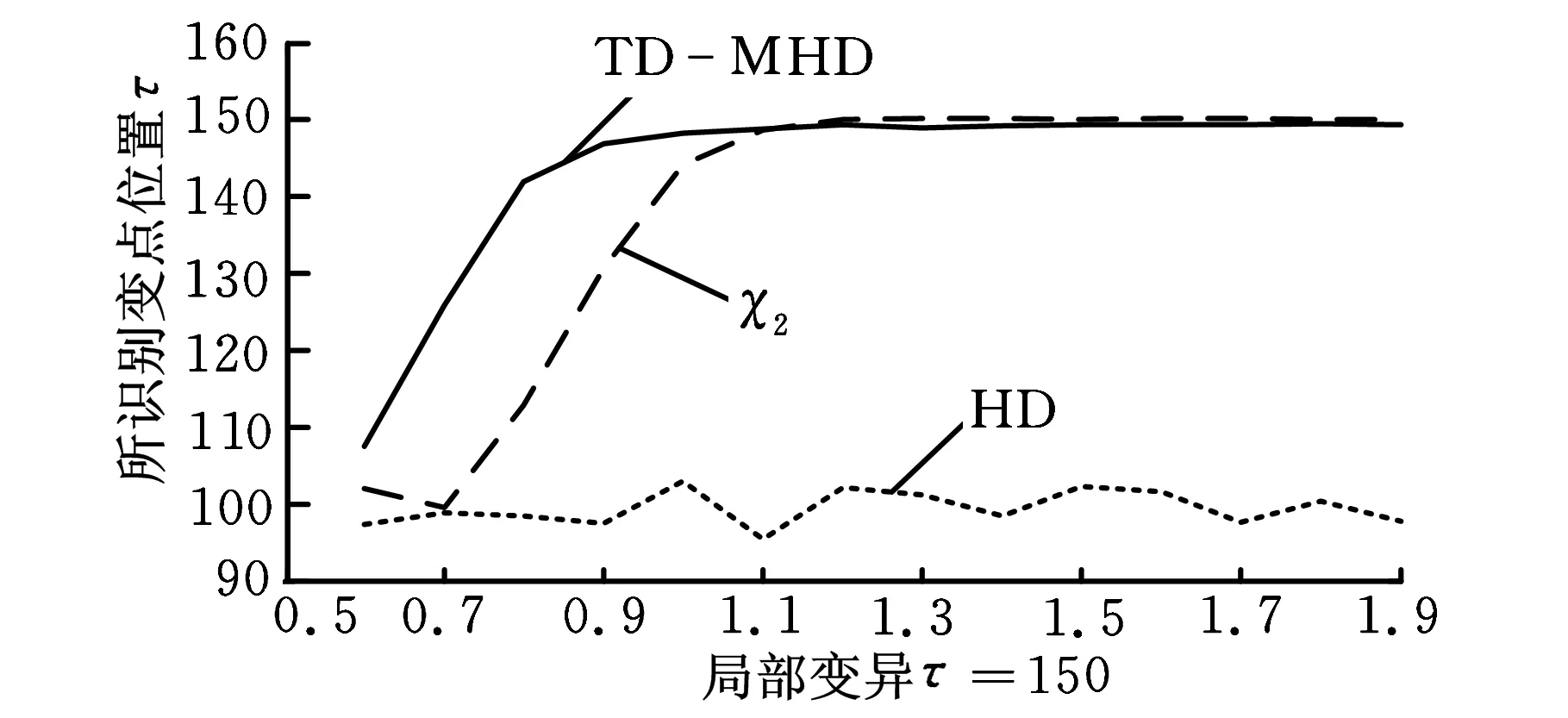
δ(i,k)j=yi j-yk ji,k=1,2,…,m;i (12) ②通过上述(m(m-1)/2)对评估值,估计对偏差值为 (13) (14) 1.4Hawkins多元T2统计量 文献[19]提出了基于多元T2统计量度来监控多元观测值变异的方法。针对式(2),在任意第k个样本位置处定义组合协方差Wk和差异性指标Zk如下: (15) (16) (17) 从而,在任意变点位置k处的T2统计量为 (18) 则当变点发生位置未知时,在所有可能发生位置中,使得统计量值最大者即为样本变异的广义似然比检验统计量,即 本文采用文献[17]的非参数轮廓模型产生一组非参数轮廓样本数据,即 yi j=10-20ae-axjsinxj+10e-axjcosxj+εi j (19) i=1,2,…,m;j=1,2,…,p 其中,εi j假定是服从于N(0,σ2)的i.i.d.正态随机变量。在本文中,每次仿真产生m=200个随机轮廓,每个轮廓维度p=100,x=0.08,0.16,…,8。参数a分别取0.5和1(σ=0.05)时的轮廓图形如图1所示。 图1 轮廓图形(σ=0.05) 本文中,假定样本数据为单变点局部变异,变点位置为τ1=50,τ2=100,τ3=150。假定在受控情况下a=0.5,σ=0.5,在变异发生后,变点之后样本在x11~x15位置发生变异,发生变异时参数a分别取0.6,0.7,…,1.9。为了真实性和可靠性,本文在任意参数情况下进行10 000次仿真。 在识别出变点位置时,本文采用校正R(即用AR表示)指标聚类评价方法分析变点识别优劣性。文献[20]将R指标和AR指标应用到变点识别方法中。对单变点识别问题而言,R指标和AR指标通过比较聚类结果的相似性来评估变点识别的准确性,聚类结果即为识别出的变点对原始样本的分类。假定变点位置检测结果为τ,则全部样本中前τ个样本受控,后m-τ个样本失控。变点位置τ将样本分为两个聚类,此种聚类结果定义为U。为了评价此聚类结果的好坏,继而评价变点位置识别的准确度,需要对实际上述聚类结果U进行评价,评价标准即为仿真假定的变点位置τ0。同理,各算法识别出变点位置的聚类结果定义为V。因此,检验变点识别准确度问题转化为检验聚类结果U与V的相似度,即当τ=τ0时U=V,此时相似度AR应为1。 为检验U与V的相似度,假设:聚类结果中, 在U和V中都属于同一类的样本个数为a;在U中属于同一类但在V中不属于同一类的样本个数为b;在U中不属于同一类但在V中属于同一类的样本个数为c;在U和V中均不属于同一类的样本个数为d。 基于此,R指标和AR指标分别为 (20) (21) 对于这两种指标,R或AR值越大表明变点识别准确度越高,其中AR指标最大值为1,即为变点完全正确识别时的情况。本文根据图1中识别出的变点位置,采用AR指标评价变点识别结果,识别结果如表1~表3所示,AR指标及其波动性如图2所示。 通过表1~表3和图2可以清楚地看到,在变点位置τ1=50,100,150时,通过TD-MHD和 表1 τ=50时AR指标 表2 τ=100时AR指标 表3 τ=150时AR指标 (a)局部变异τ=50 (b)局部变异τ=100 (c)局部变异τ=150图2 AR指标和波动性 χ2识别出的变点位置将样本集Y分为两部分。通过对这两部分的AR指标对比,表明无论变点在任何位置,当局部变异a值变化较小时TD-MHD总表现出更优异的性能。同时,随着a值的增加,两者表现出了大致相当的检测能力。但当变点位置存在样本轮廓中部时,χ2算法则完全失去了监控的能力。考虑到变点识别过程中的波动性,通过大量仿真评估AR指标的波动性可以看出,当a≤0.7时,TD-MHD的波动性相对较大;而随着a的逐渐增加,TD-MHD的波动性逐渐小于χ2算法的波动性,并且两者的波动性在a>1.3之后逐渐趋近于0时,表现出较好的稳定性。 为了更直观地展示三种方法的识别变点位置时的优劣性,图3更加直观和细化地表示出了TD-MHD、HD和χ2方法识别出的变点位置。如图3所示,当变点位置τ=50时可以看出,TD-MHD比χ2方法识别出来的变点位置更加快速地趋近于τ=50,而HD方法识别出来结果较差;当变点位置τ=100时可以看出,TD-MHD能够保持在τ=99~100位置区间,而χ2方法和HD表现出很强的波动性;同理,当τ=150时表现出与τ=50时一样的效果。综合分析,TD-MHD具有明显的优势。 (a)局部变异τ=50 (b)局部变异τ=100 (c)局部变异τ=150图3 变点识别位置 针对复杂非参数轮廓中存在局部变化的情形,本文在豪斯多夫距离算法的基础上提出一种改进的二维空间豪斯多夫距离的算法,并通过T2统计量对Phase I样本轮廓数据变点方法进行研究。通过与χ2算法进行仿真比较发现:①在检测轮廓局部偏移方面,无论变点存在于什么位置上,TD-MHD算法均能表现出优异的性能,特别是在参数变异较小的情况下更佳;②当变点位置发生在样本数据中部时,χ2算法完全失效,此时TD-MHD仍能表现优良的性能;③在识别稳定性方面,TD-MHD算法在大多数情况下都具有较好的稳定性,这对检验样本变点的鲁棒性具有重要意义。 虽然本文提出的TD-MHD算法有着很好的检测偏移和识别变点的性能,但在识别较小偏移时,特别是轮廓偏移水平远远小于误差因子时,仍存在着改进空间。同时,由于本文研究中提出的TD-MHD算法在受控情况下服从一定参数的正态分布,因此下一步将研究样本轮廓控制线能够较快地实时识别失控离群值。 [1]Hawkins D M,Qiu P,Kang C W.The Change-point Model for Statistical Process Control[J].Journal of Quality Technology,2003,35(4):355-366. [2]Kang L,Albin S L.On-line Monitoring When the Process Yields a Linear Profile[J].Journal of Quality Technology,2000,32(4):418-426. [3]Mahmoud M A, Parker P A, Woodall W H. A Change Point Method for Linear Profile Data[J].Quality and Reliability Engineering International,2007,23(2):247-268. [4]聂斌,张军军.基于T2统计量的Phase I线性轮廓局部变化变点识别方法[J].系统工程,2014,32(1):108-117. Nie Bin,Zhang Junjun.A Phase I Change-point Detection Method Based onT2Statistic to Identify the Local Changes in linear Profile[J].Systems Engineering,2014,32(1):108-117. [5]Ding Y, Zeng L, Zhou S. Phase I Analysis for Monitoring Nonlinear Profiles in Manufacturing Processes[J].Journal of Quality Technology,2006, 38, 199-216. [6]Williams J D, Woodall W H, Birch J B. Statistical Monitoring of Nonlinear Product and Process Quality Profiles[J].Quality and Reliability Engineering International, 2007, 23(8):925-941. [7]Zou C,Tsung F,Wang Z.Monitoring General Linear Profiles Using Multivariate Exponential Weighted Moving Average Schemes[J].Technometrics,2007,49(4):395-408. [8]Jensen W A,Birch J B.Profile Monitoring Via Nonlinear Mixed Models[J].Journal of Quality and Technology,2009,41(2):18-34. [9]Qiu Peihua,Zou Changliang,Wang Zhaojun.Nonparametric Profile Monitoring by Mixed Effects Modeling[J].Technometrics,2010,52(3):265-293. [10]Chicken E,Pignatiello J J,Simpson J R.Statistical Process Monitoring of Nonlinear Profile Using Wavelets[J].Journal of Quality Technology,2009,41(2):198-212. [11]邹长亮.复杂数据统计过程的若干研究[J].中国科学:数学,2013,43(8),741-750. Zou Changliang.Some Study on Statistical Process Control of Complex Data[J].Sci. Sin. Math., 2013,43(8):741-750. [12]Woodall W H.Current Research on Profile Monitoring[J].Revista Producao,2007,17(3):420-425. [13]Zhang Yang, He Zhen, Fang Juntao. Nonparametric Control Scheme for Monitoring Phase Ⅱ Nonlinear Profiles with Varied Argument Values[J].Chinese Journal of Mechanical Engineering,2012,25(3):587-597. [14]Shiau J H,Huang S L,Tsai M Y.Monitoring Nonlinear Profiles with Random Effects by Nonparametric Regression[J].Communications in Statistics-Theory and Methods,2009,38(10):1664-1679. [15]Williams J D,Woodall W H,Birch J B.Statistical Monitoring of Nonlinear Product and Process Quality Profiles[J].Quality and Reliability Engineering International,2007,23(8):925-941. [16]VaghefiA,Tajbakhsh S D,NoorossanaR. Phase Ⅱ Monitoring of Nonlinear Profiles[J].Communications in Statistics:Theory and Methods,2009,38(11):1834-1851. [17]Zhang Hang,Albin Susan.Detecting Outliers in Complex Profiles Using a Control Chart Method[J].IIE Transactions,2009,41:335-345. [18]Dubuisson M P,Jain A K.A Modified Hausdorff Distance for Object Matching[C]// Proc. International Conference on Pattern Recognition.Jerusalem,Israel,1994:566-567. [19]Zamba K D,Hawkins D M. A Multivariate Change-point Model for Statistical Process Control[J].Technometrics,2006,48(4):539-549. [20]Matteson D S,James N A.A Nonparametric Approach for Multiple Change Point Analysis of Multivariate Data[J].Journal of the American Statistical Association,2014,109,334-345. (编辑袁兴玲) A Change Point Detection Method Based on Modified Hausdorff Distance in Nonparametric Profiles Nie BinSun HuidongLi PeiDu Wenchao Tianjin University,Tianjin,300072 Change point identification in profile monitoring is an important research topic in statistical process control.Herein,the profile had nonparametric characteristics.The proposed method was based on Hausdorff distance,and could be used to measure difference between profiles.A modified Hausdorff distance algorithm was proposed to identify nonparametric profile change point.The comparison results of simulation study show that when there exists local changes in nonparametric profile,the modified algorithem has advantages in locating change points and performance stability. nonparametric profile;change point identification;Hausdorff distance;T2statistics 2014-04-21 国家杰出青年科学基金资助项目(71225006;7141123);国家自然科学基金资助项目(71102140) TH165DOI:10.3969/j.issn.1004-132X.2015.08.008 聂斌,男,1971年生。天津大学管理与经济学部副教授。主要研究方向为统计过程控制、实验设计和可靠性工程等。发表论文20余篇。孙会东,男,1990年生。天津大学管理与经济学部硕士研究生。李佩,女,1990年生。天津大学管理与经济学部硕士研究生。杜文超,男,1988年生。天津大学管理与经济学部硕士研究生。
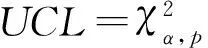
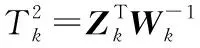
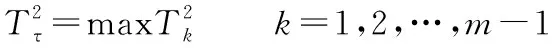
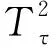
2 性能比较

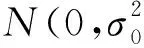
3 结论
