基于供应商选择的模块化产品族配置双层优化模型

王丹萍　杜　纲

天津大学,天津,300072

基于供应商选择的模块化产品族配置双层优化模型

王丹萍杜纲

天津大学,天津,300072

研究了供应商选取在模块化产品族配置过程中的影响,将产品族配置与供应商选择归类为主从关联优化,并建立对应的双层模型。模型上层进行产品族配置优化，以顾客效用与成本之比为优化目标，决策产品族的模块配置;模型下层进行相应模块供应商的选择优化，考虑供应商选择及供应模块的价格折扣，追求每个供应商的最大利益。针对模型为0-1混合非线性的特点，采用遗传算法求解，并以一个简化变压器产品族为例对该方法进行了说明。

产品族配置；供应商选择；主从关联优化；遗传算法

0　引言

产品族作为产品的一种扩展表现形式,具有产品定制化和规模效益的特点,已经成为理论界和企业界关注的重要主题。产品族设计与模块化配置是实现大规模定制的有效手段[1]。产品族配置即基于模块化产品平台，利用公共模块与个性化模块来配置一组满足不同细分市场需求的产品组合[2-3]。产品族配置可以在保持规模生产的同时满足定制化生产的要求。

最初的产品族配置研究关注产品族的总成本与对应的顾客满意度[4]，仅涉及产品族设计且很少涉及下游供应链的相关问题。近年来，随着生产的全球化及按订单制造等生产方式的出现，产品生产包含了越来越多的企业，产生了产品族配置与其下游供应链等结合的问题[5]，如产品族配置需要考虑供应链中模块的不同生产原则产生的影响[6]。由于产品族配置决定了产品族供应链的架构与结构，同时，产品族配置中被选择的模块也必须由供应链中相应的供应商来提供。因此,产品族配置与供应链管理是两个相关的问题，对其进行研究也很重要[7-9]。

目前对产品族与供应链的关联研究中,大多数方法将产品族配置与供应链管理这两类不同的目标集成转化为单目标优化问题[8,10]。这种“一揽子”优化的方法忽略了这两种不同决策问题之间的协调。实际上，从决策主体、目标等方面来看,产品族配置与供应链管理是一个主从关联问题。产品族配置的要求主要目标是使顾客满意度达到最大[4]；供应链的目标一般为供应链的总成本最小。产品族配置与供应链并不是彼此独立的,而是相互影响和关联的。供应链的设计目标一般要服从产品族的整体利益，同时，产品族中的模块配置对下层供应链的相关因素有着影响和约束，进而影响整个供应链的管理与设计。整体来看，二者的优化不是普通的单层问题，而是一个具有主从结构的双层优化问题，即具有两个对策主体的对策问题。

因此,本文选择了基于主从对策的理论框架，对这一问题进行研究,建立了产品族配置与供应链中供应商选择的主从优化模型,提出了包括优化模型、计算求解和应用流程等在内的一整套关联优化方法，并将方法应用于变压器产品族设计及其相关的模块供应商选择。

1　问题描述

产品族中的产品由平台模块、必选模块与可选模块组成。每个必选模块与可选模块包含可替换模块候选项，且每个模块候选项都由多个供应商供应。平台模块仅有一个模块候选项，它是所有产品所共有的，而其他模块的候选项和对应的供应商是可以进行选择的。

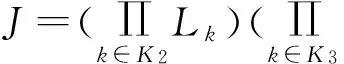
假设企业具有设计和组装所有这些产品的能力,其组装产品j的成本记为Cj。假设产品族的目标细分市场共有I个,细分市场i(i=1,2,…,I)的规模为Qi,它表示第i细分市场的客户对该种产品(包括竞争对手的同种产品)的总共需求量。客户将依据赢余(客户愿付的价格与产品实际价格的差额)购买法则来选择产品[11],如果没有一个产品能有正的赢余，他们可以不买任何产品，也可以买竞争对手的产品。市场中的客户购买意愿体现为客户对产品的效用，而客户的效用又主要取决于产品的属性和价格。因此，客户的价格效用也可以看作是一种属性，因为它不仅是客户选择的标准，而且是企业获取市场竞争优势的策略。

制造商企业在进行产品族模块配置和产品选择的同时就需要考虑相应的供应链管理和设计。本文只考虑模块的供应商选择问题,整个产品族中要生产的产品组合确定后，供应链需要对所需模块候选项的供应商进行选择。供应商决策过程中,首先进行模块供应商的选择，之后依决定对应模块价格的折扣,进而使得自己的利益最大化。供应商决策的模块价格,还需反馈到上层产品配置模型中。

本文研究的问题就是如何在优化设计和配置产品族的同时选择相应的模块供应商。供应商的选择依赖于模块的选择配置情况，处于相对从属的地位,其优化的结果也会对产品的模块配置产生影响和约束。产品族配置与模块供应商选择的优化目标具有层级的区别：产品族的模块配置以整个产品族的利益为优化目标，一般会从企业竞争优势的角度出发，追求目标市场的客户利益最大化和企业利益最大化；模块供应商的选择处于企业的技术层面，每个供应商追求自身的最大利益。

2　主从对策的决策机制

产品族模块配置和供应链的优化设计问题是一个主从对策问题,基于主从对策的理论框架可以建立问题的决策机制。决策主体中的主者为模块配置设计者L(leader),从者为供应链设计者F(follower)，这里的设计者可以是制造企业中实际的设计师、设计团体或虚拟的设计决策主体；L和F分别控制主设计向量X和从设计向量Y;决策机制是主设计者L基于自己的优化目标F(X,Y)及约束优先决定主设计向量X,并将此设计向量X发布给从设计者F，设计者F在X的条件下,基于自己的优化目标f(X,Y)及约束决定从设计向量Y,这样形成的合理反应集为

(1)

其中,D、D(X)分别为相应于主者和从者的约束集。这里假设主优化的目标是极大目标型,上层优化模型为

(2)

其中,Y(X)是给定一主设计向量X后,从设计者所能得到的最优解,由此得到最优解(X*,Y*),X*为主者的最优决策向量,Y*为从者的最优决策向量。基于这一决策机制得到的最优设计体现了模块配置与供应链的主从关系，合理反映了问题的本质结构和特征。

式(1)、式(2)可以表示成为一个双层规划模型，其一般形式为

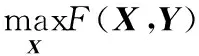
s.t. 　　　G(X)≥0

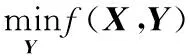
s.t.　　　g(X)≥0

(3)

此模型是一种解型双层规划，即下层模型将其最优解反馈给上层模型。上层的约束集D={X|G(X)≥0，H(X)=0},下层的约束集D(X)={Y|g(X,Y)≥0,h(X,Y)=0}。当X*∈D,Y*∈RRS(X*)且对任意X∈D,Y∈RRS(X),有F(X,Y)≤F(X*,Y*),则(X*,Y*)为式(3)的最优解。

3　优化模型

3.1产品族配置

模型的上层需要对模块配置进行决策,即在已知K种模块的J种排列中进行选择。以yj表示第j种产品方案Pj的选择变量。yj=1表示选择了生产产品Pj,yj=0表示未选择生产产品Pj。记Y=(y1,y2,…,yJ)为产品方案选择决策向量;记Xj=(Xj1,Xj2,…,XjK)为的产品Pj的表示向量,其中,Xj k=(xjk1,xjk2,…,xjkLk),xjkl(l=1,2,…,Lk)为产品Pj中模块k的第l候选项的选择变量。xjkl=1表示产品Pj中包括模块k的第l候选项,xjkl=0表示产品Pj中不包括模块k的第l候选项;Xj k为所选择生产的产品族中模块k的选择向量。整个产品族记X=(X1,X2,…,XJ),则(X,Y)构成了上层的决策向量。

上层目标函数是配置决策的依据,也是对配置决策的一种评价。评价的准则并不唯一,但最基本的准则是客户利益和企业利益的最大化。客户利益是一个综合指标，主要指客户认为产品对自己核心需求的贡献和满足程度,本文采用客户认为的产品效用来表征。假设第i细分市场的客户Si认为Pj的效用为

(4)

式中,ui k l为客户Si认为第k模块的第l候选项的效用；wj k为第k模块在Pj中的权重;πi j为Si认为Pj的综合效用;εi j为误差项。

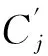
(5)

式中,Dk l为模块候选mk l测试应用的固定成本;Pk l s为供应商s对模块mk l的供应价格。

上层的目标函数综合考虑了客户和企业的利益,即以客户效用最大化与产品族成本最小化为目标，也可将这二者整合为单目标。本文采用了二者之比的形式，即将单位成本的效用最大化。考虑客户的购买量等因素后建立的目标函数为

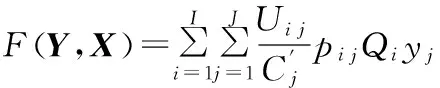
(6)

其中,pi j为客户si选择产品Pj的概率，可由已有的一些概率选择法则如基于客户效用的MNL方法[12]求得。

上层的约束条件主要是产品族的选择性要求，如产品族中的产品数量限制、两种不同产品的差异性要求、产品对公共模块的择一性要求。此外还可根据情况增加一些特殊要求，如要求模块的兼容性与不兼容性等。

3.2供应商选择

模型的下层为供应链决策，需要对配置产生的产品族中各产品的每种模块的供应商进行选择。假设下层中有S个供应商，每个供应商对模块候选项的供应能力不同，每种模块候选项只能由一个供应商供应。供应商s的目标是在将模块候选项卖给制造企业的过程中使自己的利益最大化。

对于供应商s，假设αkls表示其对模块候选项mkl的供应能力，αkls=1表示供应商s有能力供应模块候选项mkl,αkls=0表示供应商s没有能力供应模块候选项mkl;Wkls为供应商s对模块候选项mkl的最大供应量；ckls为供应商s对模块候选项mkl的单位生产成本;zkls为模块候选项mkl对供应商s的供应选择变量,zkls=1表示供应商s被选择供应模块候选项mkl,zkls=0表示供应商s未被选择供应模块候选项mkl。假设模块候选项mkl的最初价格为Pkl0s,在被选择供应后,供应商s依据订货量决策采用的供应价格折扣率为bkls。因此模块最终价格为折扣率的函数即Pkls(bkls)。供应商s的目标函数——利润为

(7)

式中,Ckls为供应商s对供应模块候选项mk l的固定成本;dk l为所有市场对模块候选项mk l的需求量。

下层的约束主要分为对供应商的选择约束与对所供应的模块候选项的价格折扣率的界约束。

3.3双层模型

基于前面两部分对上下层中重要信息的分析，可以建立产品族模块配置与供应商选择的主从对策的双层优化模型：

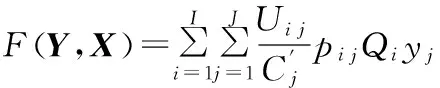
(8)

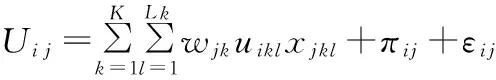
(9)

(10)

xjkl=1,k∈K1

(11)

(12)

(13)

K1+K2+K3=K

(14)

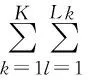
(15)

yj,xjkl∈{0,1}

(16)

(17)

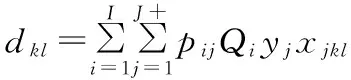
(18)

(1-αkls)zkls=0

(19)

0≤bkls≤bs max

(20)

(21)

(22)

(23)

zkls∈{0,1},bkls∈[0,1]

(24)

式(11)～式(13)表示产品中不同类型模块的选择约束;式(15)保证产品种类之间的差异性;dkl为整个市场对选择生产的产品中模块候选项mkl的总需求量;式(19)表示所选供应商有能力对模块候选项进行供应;式(20)表示供应商s对所供应模块价格的折扣必选在其最大折扣范围之内;J+为选择的产品个数;式(21)、式(23)表示每一个生产需要的模块候选项都只有一个供应商对其进行供应；式(24)表示供应商s的选择决策变量和折扣变量的取值范围。

4　求解方法

模型(式(8))的求解方法需要根据模型的复杂程度选择,常用的求解方法可分为直接方法和间接方法两类。

直接方法是依据双层规划的决策机制直接求解，一般步骤是：首先由上层模型的优化目标求出一个解，下层以该解为参变量求解下层模型。将下层得到的解反馈到上层，再次对上层进行求解，如果所得的解与原上层的解相同，此解即为整个模型的最优解；否则，采用某种优化规则进行迭代，直至得到满意的结果。

实际生产中的模块及其候选项和供应链节点及其可选方案的数量是很大的，而遗传算法在求解复杂组合优化问题上具有优越性。因此本文采用遗传算法直接对提出的双层模型进行求解。为了有效地求解模型，本文基于遗传算法设计了一个求解策略：先产生上层规划的初始种群,验证其可行性，然后将每一个可行的上层决策代入下层规划。下层规划利用遗传算法求解出最优决策和最优值，同时把最优值返回给上层来求解上层决策的适应度值。随后将上层决策种群进行选择、交叉、变异等步骤，按照此步骤循环一定的次数后得到上层规划的最优解和相应的下层问题的最优解。上述方法的流程如图1所示。

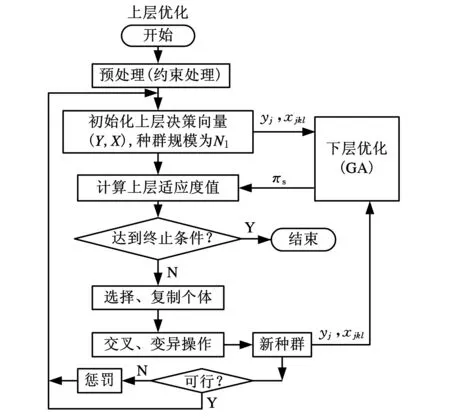
图1　求解遗传算法流程

5　案例研究

本文建立的双层模型为产品族的模块配置与供应商选择的关联优化提供了新的有效方法，但模型中有些系数与表达式需在实际应用时根据产品的具体情况确定。我们将其应用于某公司的变压器产品族的模块配置。该公司为不同的市场提供变压器产品族，且变压器产品族的架构包含公共模块(如标准化附件)、必选模块(如绝缘套管)与可选模块(如检测器)，以及各种模块对应的不同模块候选项，如图2所示。

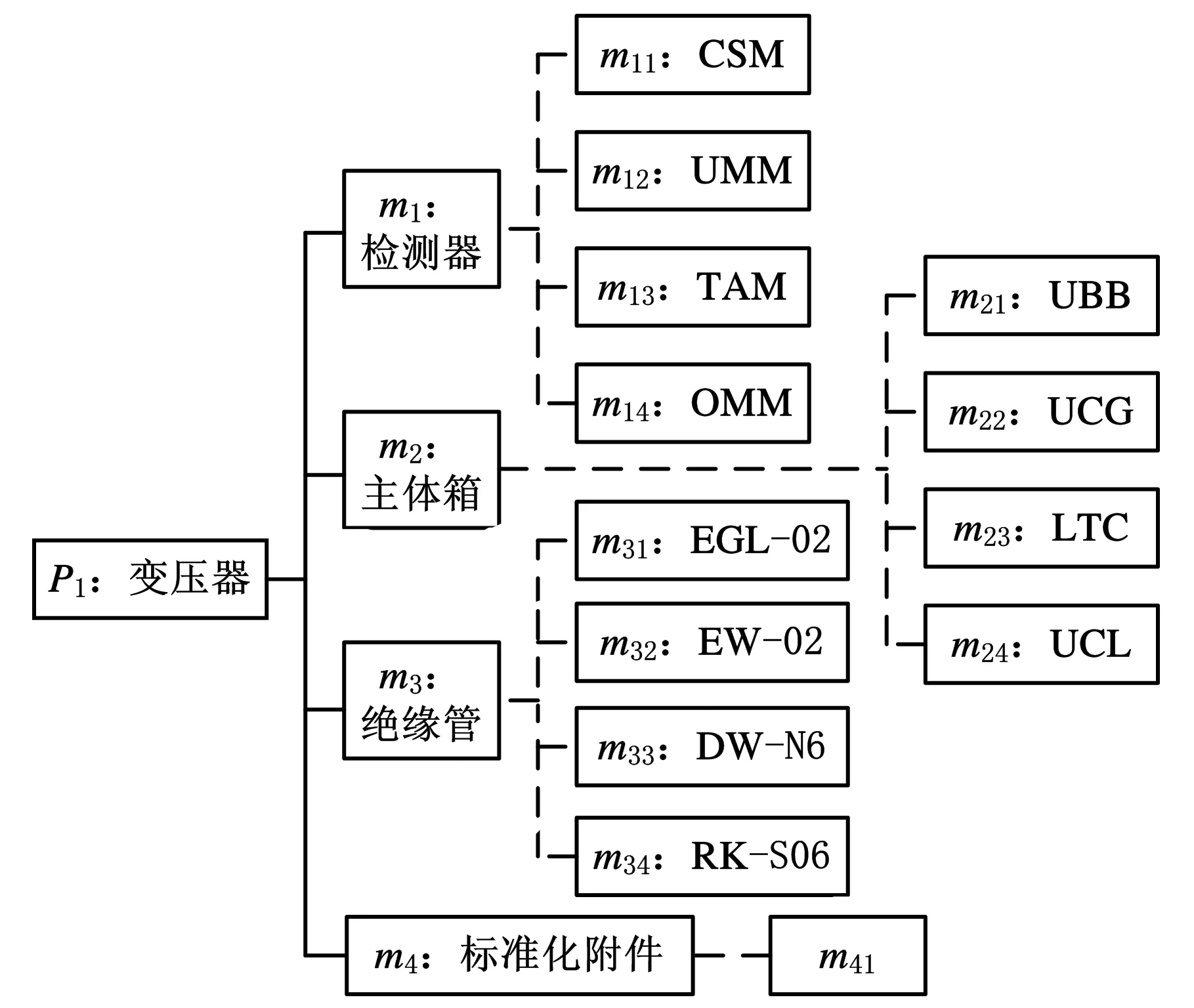
图2　变压器的产品族模块组成

如图2所示，在简化的变压器产品模块组成中，m1为可选模块且有4个模块候选项；m2与m3为必选模块，各自有4个模块候选项；m4为公共模块，只有1个模块候选项。各模块的模块候选项均用其英文简化字母表示，各自的作用与区别在这里就不进行详细说明了。

这个变压器产品族就是在所有可选模块和必选模块中选择不同模块候选项，来组合成一个满足市场需求且能最大化顾客满意率的一个产品组合。传统的变压器的产品族配置都是给出模块成本，但在考虑到供应链中模块供应商的选择时，产品族的配置就成为Stackelberg对策问题,因此构建产品族配置与供应商选择的双层模型。在这样的双层模型中,上层模块的成本可以通过下层的决策获得，模型的Stackelberg均衡解可以通过遗传算法得到。假设企业向市场提供有两种产品组成的产品组合，即J+=2。

在不影响模型本质情况下作适当简化,假设只考虑一个主要的目标市场,即I=1，市场规模Qi取为适当的固定值1000，市场对产品的选择概率pij设为等概率。同时假设整个企业对所有产品的组装成本都相同,设Cj=378。模块候选项在企业中的测试成本Dk l各不相同，如表1所示。

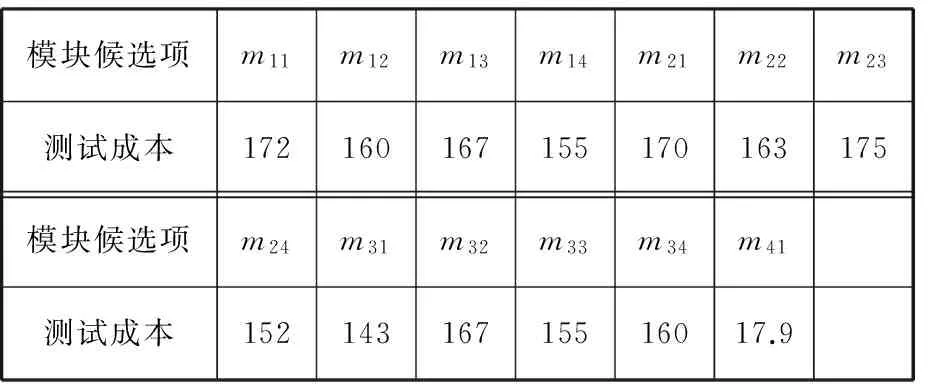
表1　模块候选项的测试成本

上层优化的目标函数是最大化顾客效用与成本之比。在上层模型的效用函数中， 每个模块在产品中所占的权重Wjk均相等,每件产品的效用值πj为产品所包含模块对应效用值的固定复合效用值。

本文利用联合分析方法估计效用值，主要步骤如下：先选取一定数量的消费者,请他们分别对各种模块的模块候选项组合方案进行排序，每个消费者把自己最喜欢的组合放在第一位，最不喜欢的放在最后一位。然后利用统计软件SPSS的效用分析模块得出消费者对模块候选项的效用值。

具体计算时,首先利用SPSS软件对组合出的所有产品进行正交分析，正交分析的结果是产生出代表性的产品集合。然后选择100名消费者对这个产品集合中的产品进行评价和排序。最后利用SPSS进行联合分析计算，得出消费者对模块候选项的效用值。文章中，变压器产品族中所有模块候选项对应的效用值如表2所示。

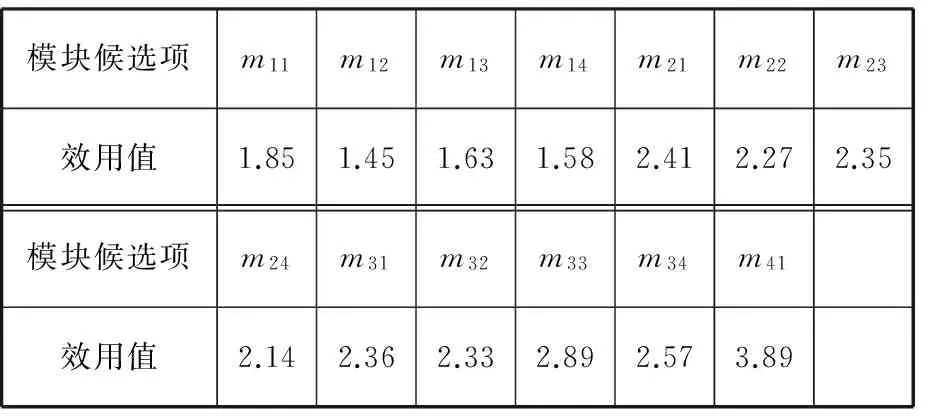
表2　通过联合分析得到的模块候选项的效用值

模块候选项的供应商候选项情况如表3所示,模块候选项的价格为折扣率与其原始价格的线性组合，即Pkls=Pkl0sbkls。应用遗传算法对上面关于产品族配置与模块供应商选择的双层优化模型进行求解，可以得到最优解或近似最优解。设置变异概率为0.05，交叉概率为0.80,经过100次的迭代就可以得到模型的最优解。图3给出了上层遗传算法的种群的最优个体对应的函数值随迭代次数的变化趋势。从图3可以看出，最优解的评价函数是迭代次数的单调增函数,这说明了

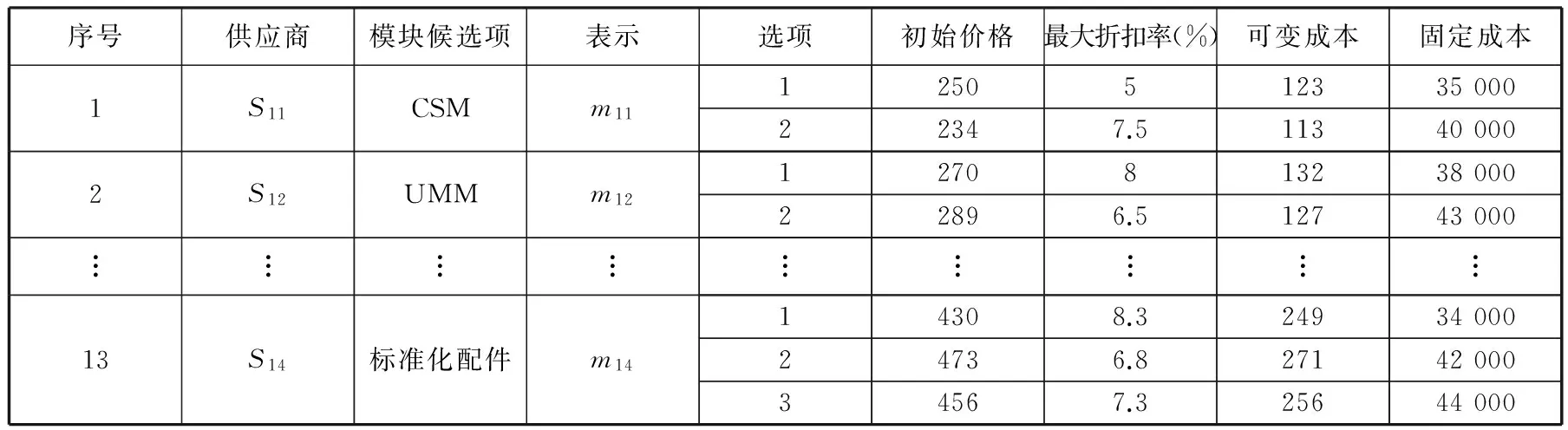
表3　模块候选项的供应商候选项信息

遗传算法对该双层模型求解过程的寻优性与收敛性。优化后的结果如下:产品P1的模块组成为m14(OMM)、m22(UCG)、m31(EGL-02)与m41(标准化附件)，产品P2的模块组成为m11(CSM)、m21(UBB)、m32(EW-02)与m41(标准化附件)。

图3给出的是上层遗传算法的每代种群的最优个体对应的适应度值和平均适应度值随迭代次数的变化趋势,体现了算法的收敛性。模型结果说明,案例中的制造商在其生产能力等约束下生产产品P1和P2可以使效用成本比最大化,其最大值为1.7919。决策得到了对应模块的供应商选择及每个供应商的折扣率与最大利润。

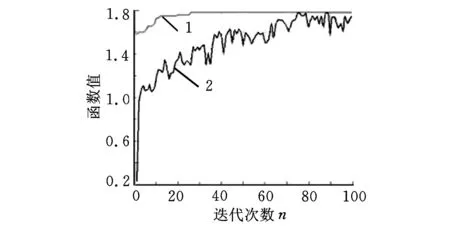
1.最优个体的适应度值　2.平均适应度值图3　遗传算法求解趋势图

6　结语

产品族的模块配置过程中，考虑供应商的选择使得产品的模块选择不是选择效用与成本之比最大的结果(由下层供应商对其进行了约束);供应商的选择方案同样受到模块配置的影响。

采用本文提出的模型与方法设计变压器产品族,实现了产品族模块配置与相应供应商选择的主从优化,实现了客户与企业利益的综合优化。

但模型只考虑了模块供应商的选择,而对供应链管理中的其他主体如制造商、组装商、分销商则没有考虑，同时没有考虑供应链管理中的库存管理、订货管理等方面的因素。因此在以后的研究中可以扩展对供应链管理等方面的研究。本文提出的模型,在应用中还可以进行完善和补充,比如在上层可以增加某些细分市场对产品族中相应产品的特殊要求(特定模块候选项)的约束等。

[1]JiaoJ，TsengM，DuffyV，etal.ProductFamilyModelingforMassCustomization[J].Computers&IndustrialEngineering,1998,35(3/4):495-498.

[2]SimpsonT.ProductPlatformDesignandCustomization：StatusandPromise[J].ArtificialIntelligenceforEngineeringDesign,AnalysisandManufacturing，2004，18(1):3-20.

[3]SimpsonT，MaierJ，MistreeF.ProductPlatformDesign：MethodandApplication[J].ResearchinEngineeringDesign，2001,13(1):2-22.

[4]JiaoJ，SimpsonT，SiddiqueZ.ProductFamilyDesignandPlatform-basedProductDevelopment：AStartoftheArtReview[J].JournalofIntelligentManufacturing，2007，18(1)：5-29.

[5]ElMaraghyH,MahmoudiN.ConcurrentDesignofProductModulesStructureandGlobalSupplyChainConfigurations[J].InternationalJournalofComputerIntegratedManufacturing,2009,22(6):483-493.

[6]LamotheJ,Hadj-HamouK,AldanondoM.AnOptimizationModelforSelectingaProductFamilyandDesigningItsSupplyChain[J].EuropeanJournalofOperationalResearch,2006,169(3):1030-1047.

[7]HuangG,ZhangX,LiangL.TowardsIntegratedOptimalConfigurationofPlatformProducts,ManufacturingProcessesandSupplyShains[J].JournalofOperationsManagement,2005,23(3/4):267-290.

[8]ShahzadM,Hadj-HamouK.IntegratedSupplyChainandProductFamilyArchitectureunderHighlyCustomizedDemand[J].JournalofIntelligentManufacturing,2013,24(5):1005-1018.

[9]ElHadjR,AgardB,PenzB.SimultaneousDesignofaProductFamilyandItsRelatedSupplyChainUsingaTabuSearchAlgorithm[J].InternationalJournalofProductionResearch,2011,49(19):5637-5656.

[10]FujitaK,AmayaH,AkaiR.MathematicalModelforSimultaneousDesignofModuleCommonalizationandSupplyChainConfigurationTowardGlobalProductFamily[J].JournalofIntelligentManufacturing,2013,24(5):991-1004.

[11]KaulA,RaoV.ResearchforProductPositioningandDesignDecisions:AnIntegrativeReview[J].InternationalJournalofResearchinMarketing,1995,12(4):293-320.

[12]Ben-AkivaL.DiscreteChoiceAnalysis:TheoryandApplicationtoTravelDemand[D].Cambridge,USA:MassachusettsInstituteofTechnology,1985.

(编辑张洋)

Bi-level Optimization Model for Product Family Configuration Based on Supplier Choosing

Wang DanpingDu Gang

Tianjin University,Tianjin,300072

The paper presented the effects of supplier selection in modular product family configuration.A new method for product family optimization:leader-followers joint decision making model was presented herein.The model consisted of two optimization levels:an upper level and a lower level.The upper level determined product family configurations by selecting the components to be assembled for the customer perceived utility per cost form both the customer and engineering perspectives.The lower level designed the supply chain of the product family by choosing suppliers for the supplier’s interests.A genetic algorithm was proposed to solve the model.A design example of a simple product family was provided to demonstrate the method.

product family configuration;supplier choosing; leader -follower joint optimization;genetic algorithm

2014-05-30

国家自然科学基金资助项目(71371132)

F273；TH164DOI：10.3969/j.issn.1004-132X.2015.08.014

王丹萍,女,1985年生。天津大学管理与经济学部博士研究生。主要研究方向为管理系统分析与决策、产品族优化。杜纲,女,1954年生。天津大学管理与经济学部教授、博士研究生导师。