基于LCD的齿轮箱混合故障盲源分离研究

杨　宇　李永国　何知义　程军圣

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

基于LCD的齿轮箱混合故障盲源分离研究

杨宇李永国何知义程军圣

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

盲源分离是一种有效的混合故障诊断方法,而局部特征尺度分解(LCD)是非平稳信号的有效分析处理工具，综合两者的优点，提出了基于LCD的齿轮箱混合故障盲源分离方法。将源信号LCD分解，得到新的多维信号，采用Bayesian信息准则(BIC)估计盲源的数目并对多维信号进行重组。最后进行联合近似对角化处理，实现源信号的盲分离。仿真和实验结果表明，该方法能够有效地实现齿轮箱混合故障盲源分离。

盲源分离;局部特征尺度分解;齿轮箱;故障诊断

0　引言

齿轮箱在机械设备中的应用非常广泛,是设备中传递动力的重要部件,因而齿轮箱的故障诊断具有重要意义。国内外专家学者在动力学建模[1]与动态信号处理两方面开展一系列研究工作。目前,在信号处理方面,小波变换[2]、经验模态分解[3]、局部均值分解[4]等方法已经应用于齿轮箱故障诊断中,并取得一定成果。

盲源分离(blind source separation,BSS)是机械故障诊断的有效方法[5],它不依赖任何先验知识,就能将源信号从观测信号中分离开来。现有的盲源分离方法为获得较好的分离效果,往往假设信号的源数小于或者等于信号的观测数。但是,在机械故障诊断中，BSS算法的源数假设条件很难满足，观测信号的数目通常要小于源信号的数目。信号的时频分析方法为上述问题即欠定盲源问题的解决提供了新思路。

文献[6]提出了局部特征尺度分解(local characteristic scale decomposition,LCD)方法,该方法可以将复杂的非平稳振动信号分解为若干瞬时频率具有物理意义的平稳内禀尺度分量(intrinsic scale component,ISC)。相对于EMD算法,LCD算法在分解速度、端点效应、迭代次数方面更加优越，并且该方法具有良好的自适应性[7]。因此,本文将LCD方法引入混合故障盲源分离中,提出了基于LCD的齿轮箱混合故障盲源分离方法。该方法能够满足传统盲源分离中要求源信号平稳、非高斯及相互独立的假设，并且还可以解决观测信号数目少于源信号数目的欠定问题。仿真和实验结果表明，该方法可以有效用于齿轮箱的盲源分离。

1　局部特征尺度分解

LCD方法假设任何复杂信号由不同的ISC分量组成,任何两个ISC分量之间相互独立,这样任意一个信号x(t)就可以被分解为有限个ISC分量之和,其中任何一个ISC需满足以下两个条件：

(Ⅰ)整个数据段内,极大值为正,极小值为负,且任意两个相邻的极大值与极小值之间呈现单调性。

(Ⅱ)整个数据段内,设存在极值Xk(k=1,2,…,M),其对应的时刻为τk,其中,M为极值点个数。由任意两个相邻的极大(或极小)值点(τk,Xk)、(τk+2,Xk+2)确定的直线lk：y=(Xk+2-Xk)(t-τk)/(τk+2-τk)+Xk在二者之间的极值点Xk+1所对应的时刻τk+1处的函数值Ak+1与Xk+1满足：

aAk+1(1-a)Xk+1=0a∈(0，1)

(1)

(2)

满足上述条件(Ⅰ)、(Ⅱ)的单分量信号,本文称之为内禀尺度分量。条件(Ⅰ)要求相邻的极值之间具有单调性，保证波形的单一。条件(Ⅱ)是为了保证得到的ISC的波形的光滑性和对称性。条件(Ⅰ)、(Ⅱ)保证了ISC分量在任意极大值点和相邻的极小值点之间具有单一模态。

对实信号Xt(t≥0),LCD分解步骤大致如下：

(1)确定信号Xt的极值点(τk,Xk)。得到基线信号的纵坐标：

Lk=aAk+(1-a)Xk=2，3,…,M-1

(3)

其中,Ak可根据式(2)得到。

(2)由于Lk的值是从L2到LM-1,需要估计端点L1、LM的值,因此需要对序列进行延拓。通过延拓,得到左右两端极值点(τ0,X0)、(τM+1,XM+1)。令k分别等于0和M-1,按式(3)求出L1与LM的值。然后，再用三次样条函数拟合所有的Lk，得到均值曲线B1(t)。

(3)将均值曲线从原信号中分离出来，即

h1(t)=Xt-B1(t)

(4)

若h1(t)是一个ISC,输出h1(t)并令C1=h1(t)。否则将h1(t)作为原始数据,继续重复上述步骤(1)～(3),直到h1k(t)是一个ISC,记C1=h1k(t)。

(4)将C1从原始数据中分量出来,即

u1(t)=Xt-C1

(5)

得到一个新的剩余信号u1(t)。

(5)再将u1(t)视为原始数据,重复上述步骤(1)～(4),重复循环n-1次,直到剩余信号un(t)为一单调或常函数,于是

(6)

2　基于LCD的盲源分离方法

2.1源数估计方法

为解决单通道信号的盲源分离问题,首先要对源信号的数目进行估计。Bayesian信息准则[8](Bayesian information criterions,BIC)是在Minaka Bayesian选择模型(Minaka Bayesian,MIBS)的基础上发展而来的源数估计方法,适用于分析非高斯源信号,因此可以用来估计机械振动源信号的数目。MIBS的目标是找到一个能够使得代价函数最大的序号n(n=1,2,…,l),l为非零特征值的个数。此时,序号n即为观测信号x1(t)所隐含的维数。MIBS可用Bayesian信息准则近似,Bayesian信息准则为

(7)

(8)

dk=lk-k(k+1)/2

(9)

式中,N为计算协方差矩阵数据的长度;λj为协方差矩阵的主特征值,且λ1≥λ2≥…≥λl。

2.2联合近似对角化

联合近似对角化[9]算法主要包括两步:

(1)预白化。白化矩阵W由Rx(0)求得,Rx(0)=E[x(t)xT(t)]为观测信号x(t)在τ=0时的自相关矩阵。令m×n阶矩阵Rx(0)的特征值降序排列为λ1,λ2,…,λm,对应的特征向量为h1,h2,…,hm,则白化矩阵为

(10)

观测信号x(t)左侧乘W即可得到白化观测信号z(t),即

z(t)=Wx(t)=WAs(t)=Us(t)

(11)

式中,U为酉矩阵。

(2)分离。定义参照函数：

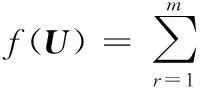
(12)

式中,M为m阶方阵;Qz(M)为白化信号z(t)的四阶累积量矩阵。

取式(12)的最大值,得到酉矩阵U。进而得到估计的源信号：

(13)

2.3LCD-BSS方法

为解决欠定盲源分离问题,利用LCD方法将单通道信号分解，并与其ISC组成新的多维矩阵,将欠定盲源分离转化为普通盲源分离。基于此,论文提出了基于局部特征尺度分解的齿轮箱混合故障盲源分离方法,简称LCD-BSS方法。该方法的流程如图1所示。

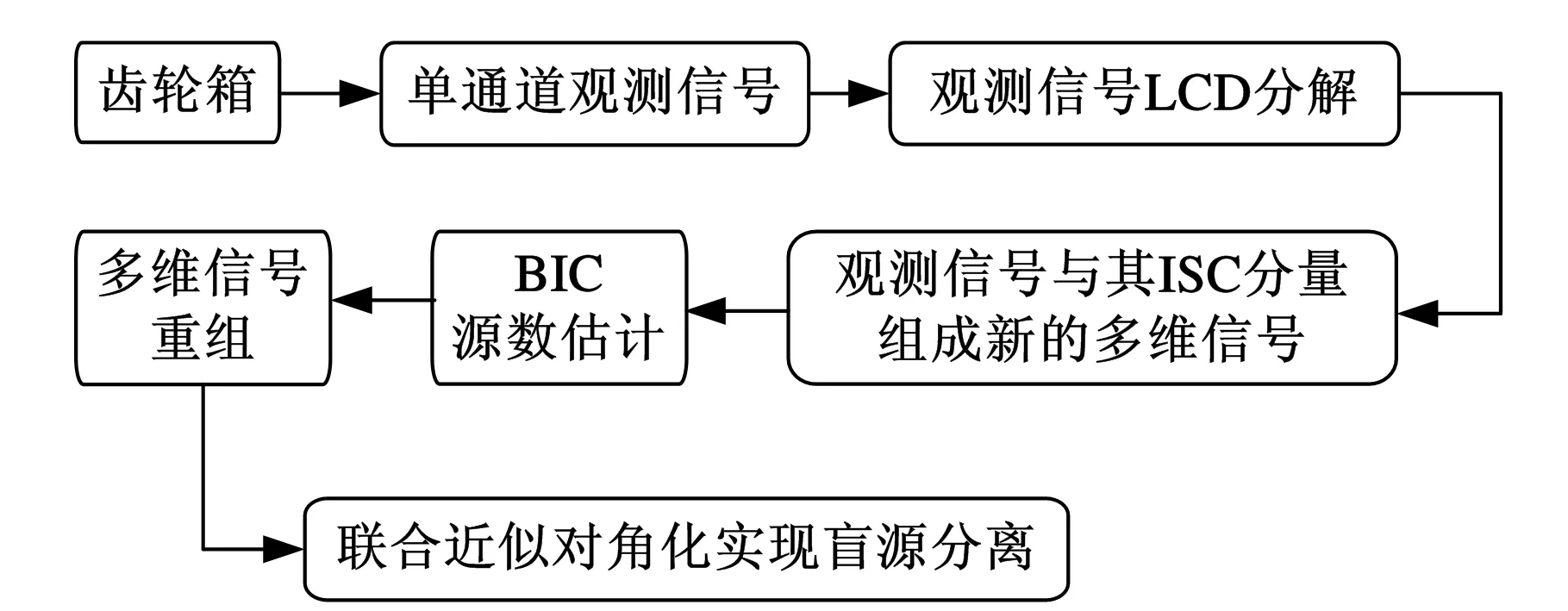
图1　LCD-BSS方法流程框图

LCD-BSS方法的具体步骤如下：

(1)采集振动信号。利用采集设备对齿轮箱的振动信号进行采集,得到单通道观测信号x1(t)。

(2)LCD方法分解观测信号。对单通道观测信号进行LCD分解得到其ISC:

x1isc=(c1,c2,…,cn,rn)

(3)源数估计。单通道信号x1(t)和它的ISC组成新的多维信号

xisc=(x1(t),c1,c2,…,cn,rn)

并根据Bayesian信息准则估计信号源数。

(4)信号重组。单通道信号x1(t)和它的ISC分量重组得到多维信号x=(x1(t),c1,c2,…),x的维数等于估计的信号源数。

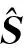
3　仿真

齿轮箱中,齿轮和轴承是两个重要零件,齿轮调节转轴的转速,而轴承则支撑着转轴。齿轮发生故障时,会出现幅值调制与相位调制现象,其振动信号的模型为

式中,fg为啮合频率;φk为第k次谐波成分的相位。

滚动轴承的振动信号模型为

sb(t)=(1+βsin(2πf2t))sin(2πf1t)

式中,β为调幅系数,f1为轴承的内(外)圈特征频率;f2为旋转频率。

为了验证LCD-BSS方法的有效性,本文构造如下3个振动源信号：

采样频率fs=1024 Hz,采样点数为512。源信号时域及频域波形如图2所示。

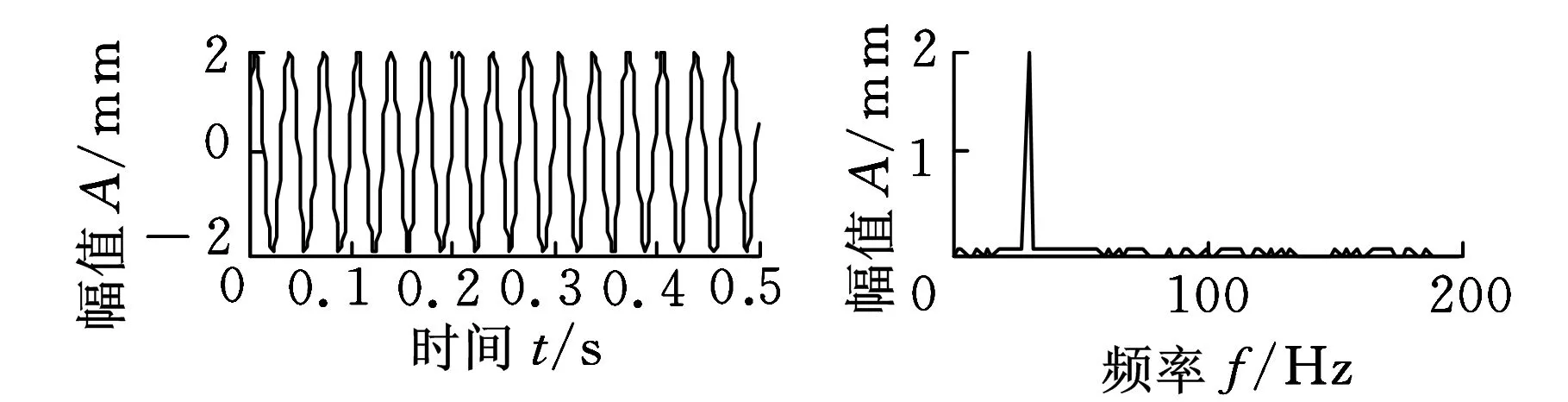
(a)振动信号源1

(b)振动信号源2

(c)振动信号源3图2　源信号的时域、频域波形

设有n个信号源、m个传感器,则根据振动源信号混叠模型,有x(t)=As(t)。其中,x(t)=[x1(t)x2(t)…xm(t)]T表示m个传感器的输出,s(t)=[s1(t)s2(t)…sn(t)]T表示n个相互独立的未知源信号,这n个源信号瞬时线性混叠得到x(t);m×n阶矩阵A为混合矩阵。为得到虚拟的传感器观测信号,文中A为1×3的随机矩阵,其元素在0到1之间均匀分布。构造得到某一观测信号,其时域及频域波形如图3所示。对观测信号通过Bayesian信息准则进行源数估计,由图4可知,源信号的数目为3,与初始假设一致。

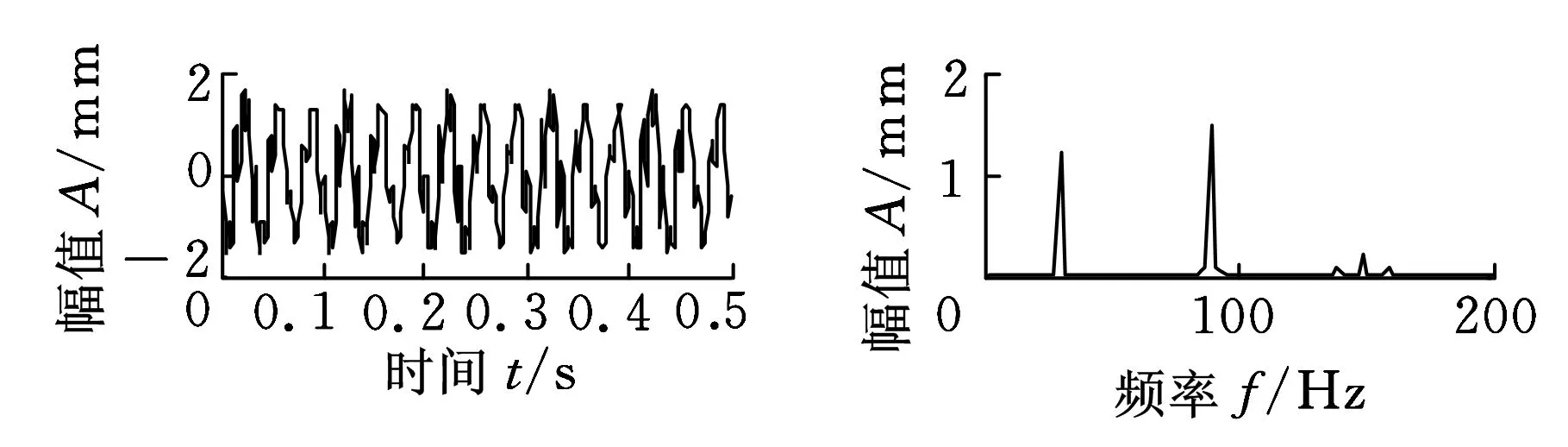
图3　观测信号的时域、频域波形

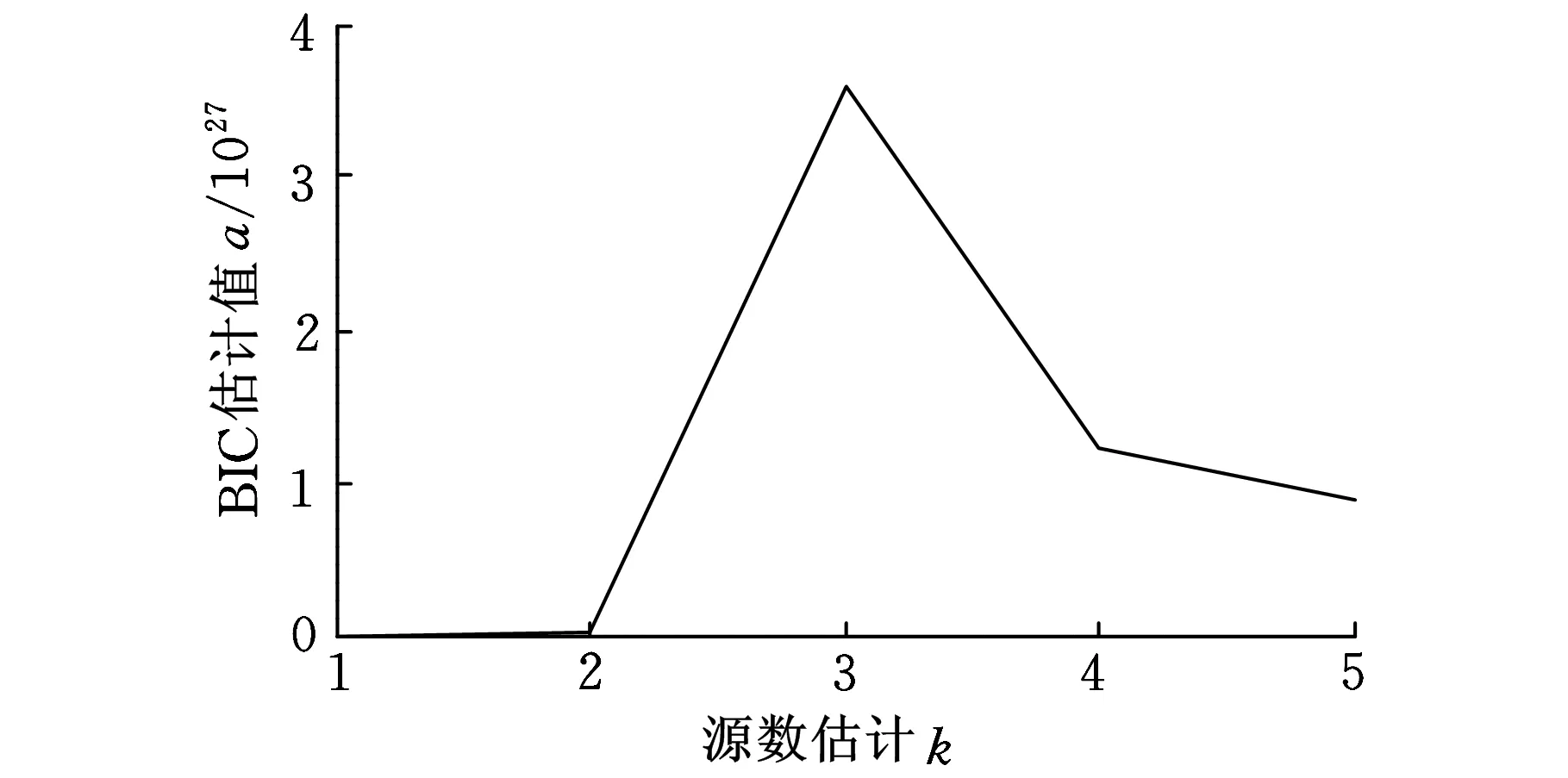
图4　观测信号的源数估计值

由于源信号数目为3,取观测信号x1(t)的内禀尺度分量x1isc=(c1,c2,…,cn,rn)的前2个分量,和单通道信号x1(t)重组为新的三维信号x=(x1,c1,c2)。对重组的三维信号x=(x1,c1,c2)进行联合对角近似化,实现其盲分离,得到的分离信号时域及频域波形如图5所示。

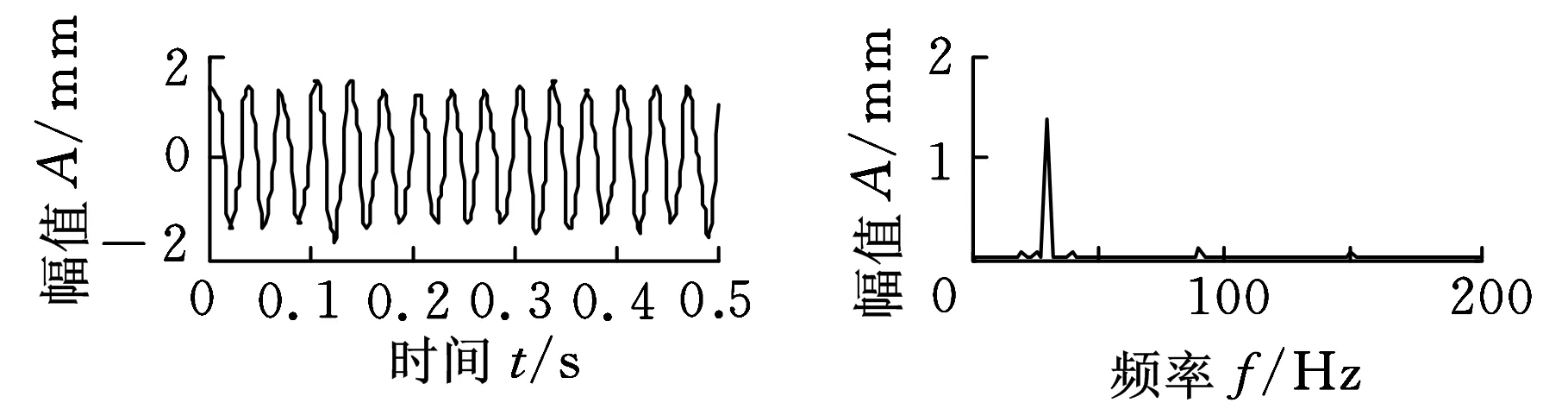
(a)信号x1

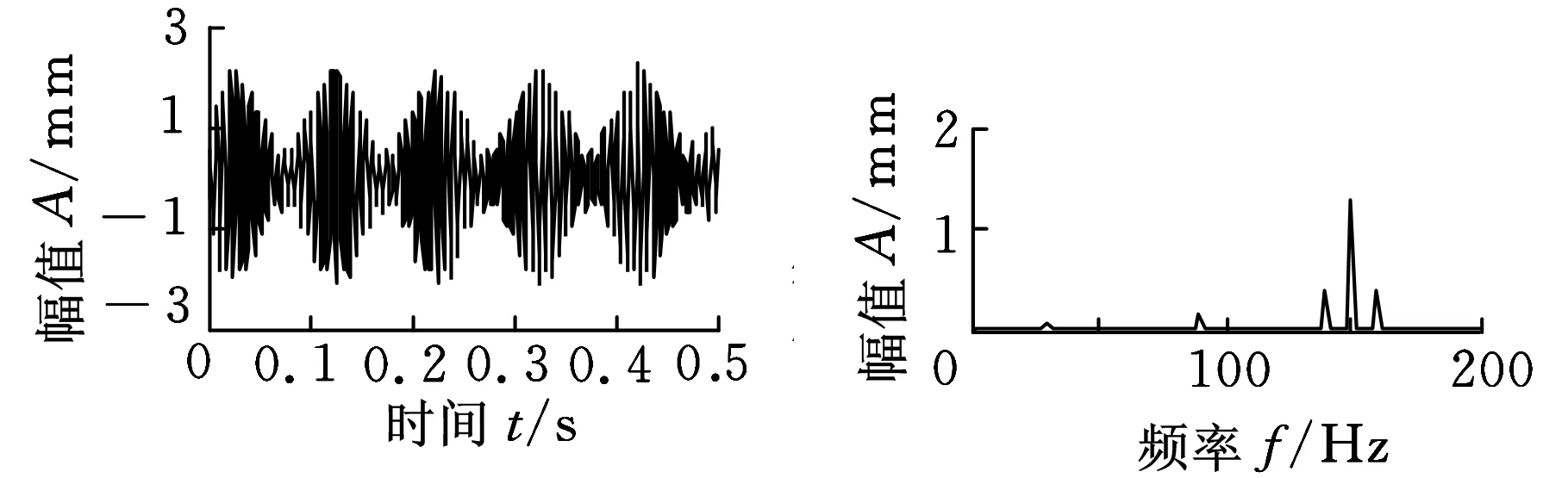
(b)信号c1

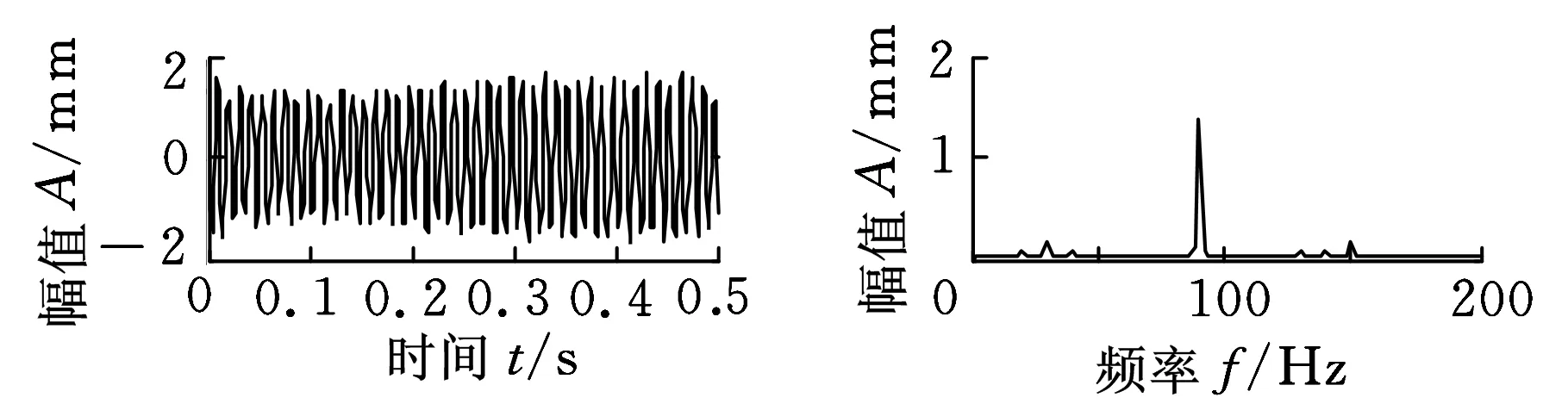
(c)信号c2图5　分离信号时域、频域波形

对比图2、图5可知,虽然图5中的3个分离信号的幅值和信号的顺序产生了变化,但是图5分离得到的信号的时域图和频谱图波形基本吻合，源信号得到较好的分离。因此,LCD-BSS方法可以用于盲源信号的分离。

4　实例分析

为了验证所提方法在实际中的可行性,对某一齿轮箱的轴承和齿轮进行了实验。故障是通过激光切割的方式在齿轮、轴承内圈、轴承外圈上设置的混合故障。齿轮的齿数为37,其槽深度为1 mm;轴承的型号是6307,其点蚀深度为0.2 mm。转轴的转速为900 r/min,即轴的基频fr=15 Hz,采样频率fs=8192 Hz。齿轮的啮合频率为555 Hz,轴承外圈的故障特征频率46 Hz,内圈的故障特征频率为74 Hz。通过加速度传感器采集振动信号，得到的混合故障振动信号如图6所示。

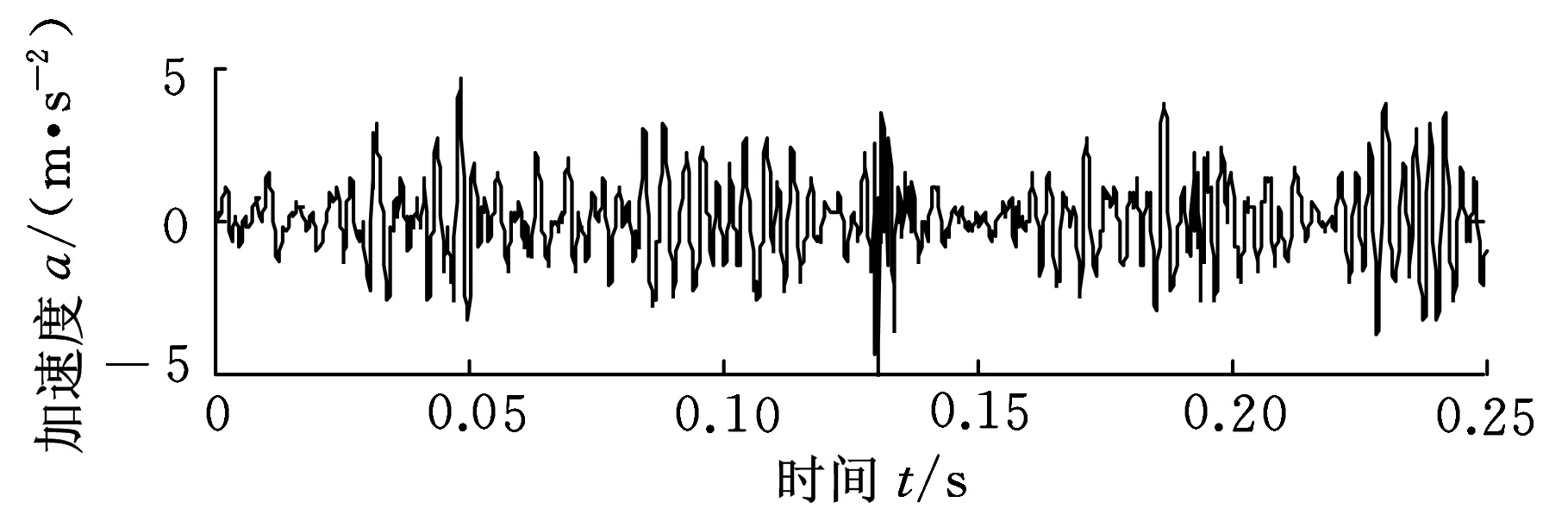
图6　混合故障信号时域波形

利用LCD方法对其进行分解,得到新的多维信号,用Bayesian信息准则对源信号源数估计,由图7可知，源数为3，与设置故障数目一致。用论文提出的分离方法对该混合故障观测信号进行盲分离，得到的估计的源信号。其中，得到的白化矩阵为

得到的酉矩阵为

对得到的估计源信号进行频谱分析,结果如图8所示。由图8可知,图8a在44 Hz处出现峰值,与轴承外圈故障特征频率46 Hz接近,对应着轴承外圈故障;图8b在556 Hz处出现峰值,与齿轮的故障特征频率555 Hz接近,对应着齿轮故障;图8c在76 Hz处出现峰值,与轴承内圈故障特征频率74 Hz接近,对应着轴承内圈故障。因此,论文中提出的LCD-BSS方法可以很好地将混合故障分离开来,可以将该方法应用于混合故障分离研究。

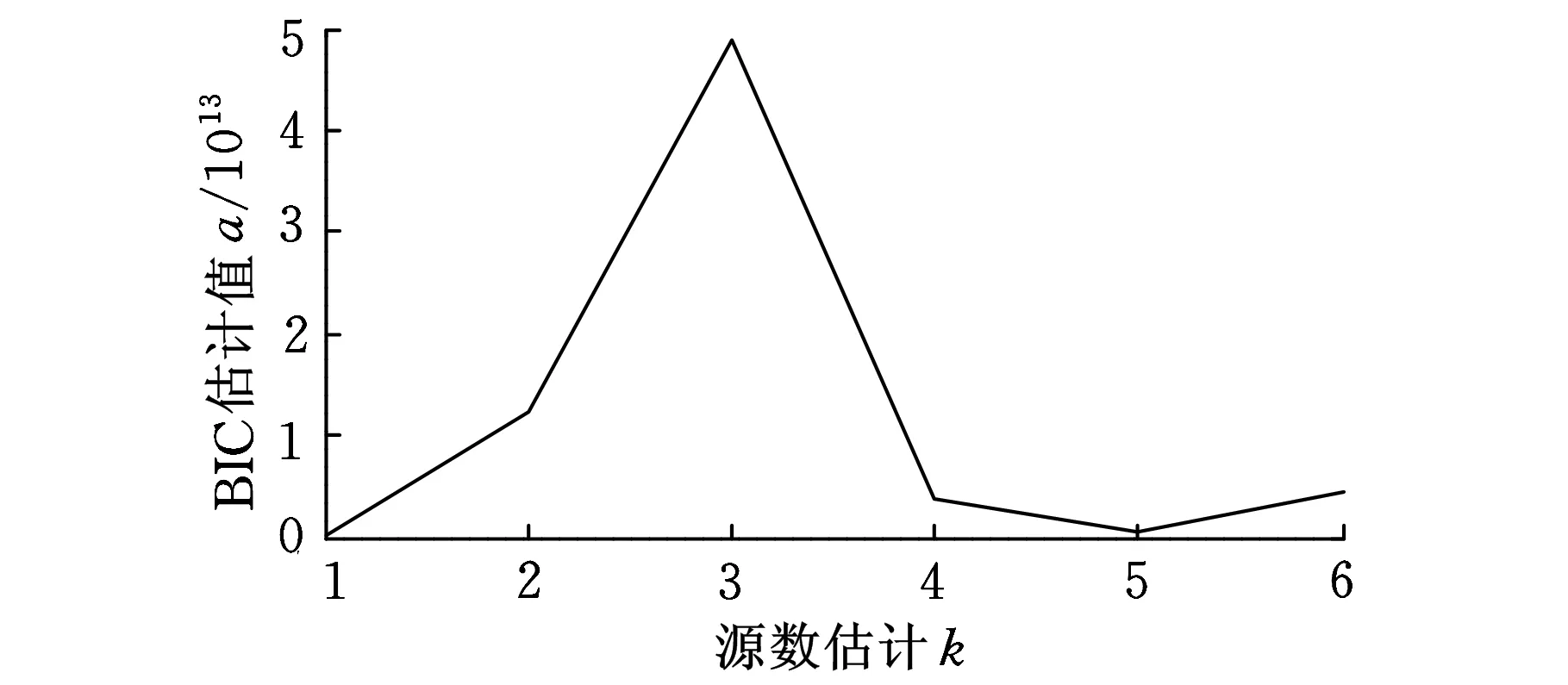
图7　混合故障信号源数估计

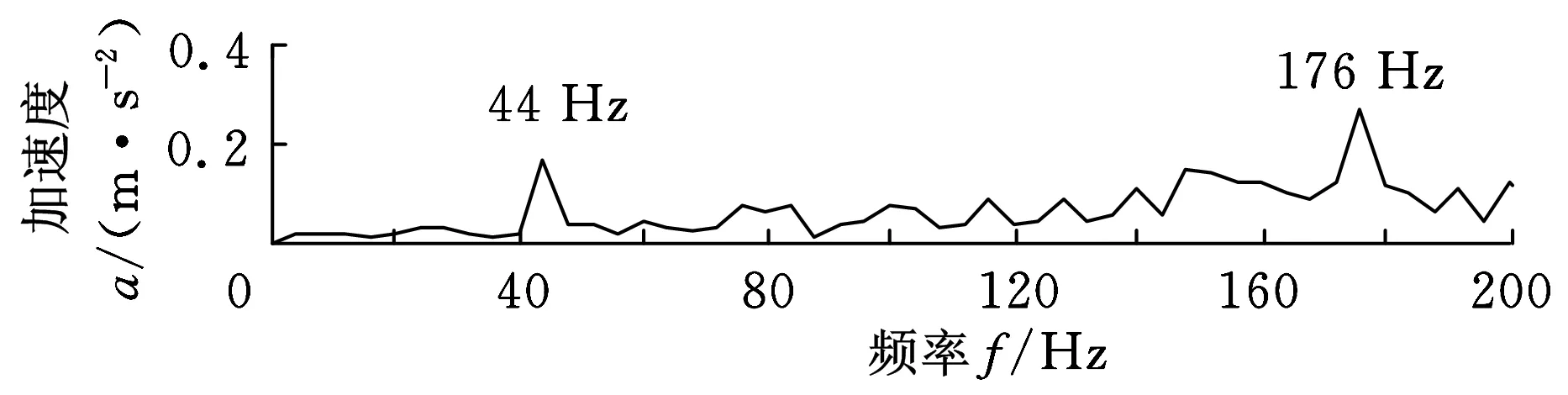
(a)外圈故障

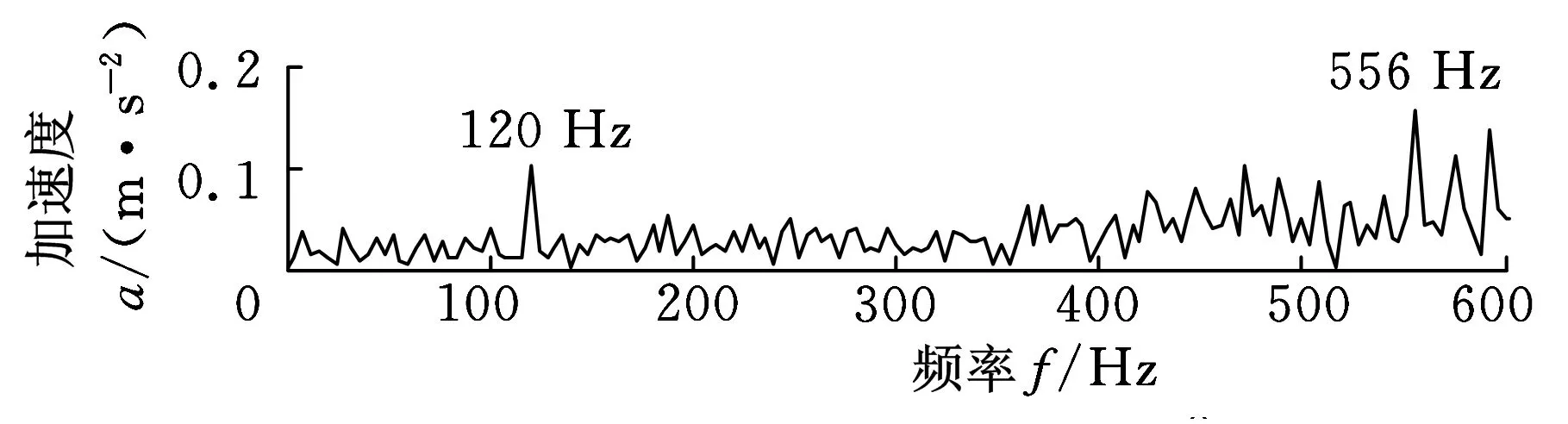
(b)齿轮故障

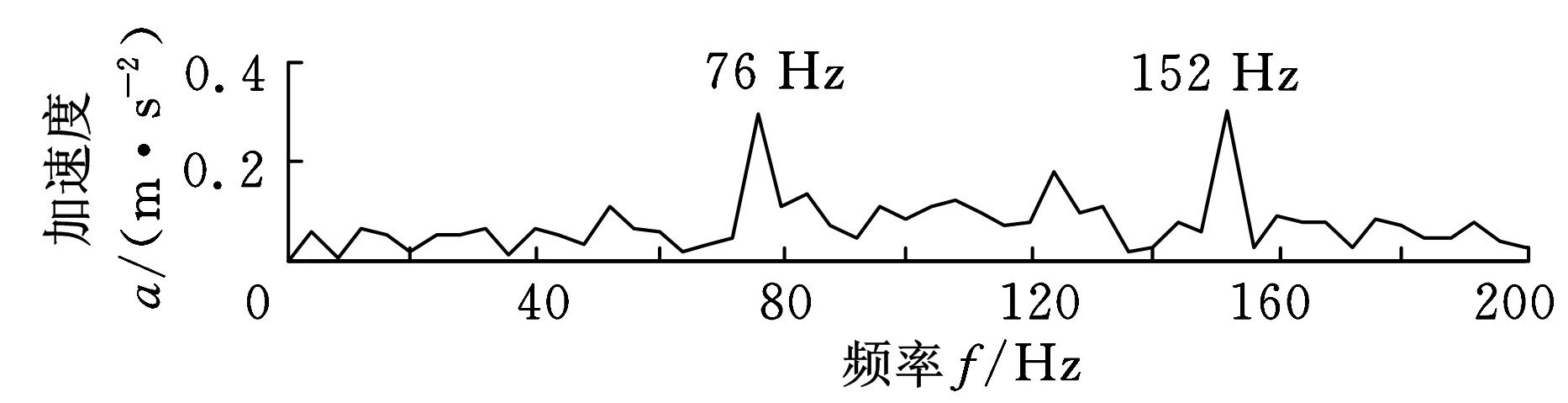
(c)内圈故障图8　分离信号的频谱图

5　结语

本文综合LCD和盲源分离的优点,提出了基于LCD的齿轮箱混合故障盲源分离方法。单通道信号经LCD分解后重组得到新的多维信号，然后通过BIC对盲源数目进行估计，确定源数，最后采用联合近似对角化方法得到估计的源信号。仿真和实例研究表明,LCD-BSS方法适合用于非平稳信号的混合故障盲源分离问题,能够有效地实现齿轮箱混合故障信号的源数估计和盲源分离,为齿轮箱故障诊断提供了新的方法。

[1]Guo Yichao,Parker R G. Purely Rotational Model and Vibration Modes of Compound Planetary Gears[J].Mechanism and Machine Theory,2010,45(3):365-377.

[2]Li Hui,Zhang Yuping,Zheng Haiqi.Application of Hermitian Wavelet to Crack Fault Detection in Gearbox[J].Mechanical Systems and Signal Processing,2011,25(4):1353-1363.

[3]雷亚国,孔德东,李乃鹏,等.自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J].机械工程学报,2014,50(3):64-70.

Lei Yaguo,Kong Detong,Li Naipeng,et al.Adaptive Ensemble Empirical Mode Decomposition and Its Application to Fault Detection of Planetary Gearboxes[J].Journal of Mechanical Engineering,2014,50(3):64-70.

[4]张亢,程军圣,杨宇.基于局部均值分解的阶次跟踪分析及其在齿轮故障诊断中的应用[J].中国机械工程,2011,22(14):1731-1736.

Zhang Kang,Cheng Junsheng,Yang Yu.Order Tracking Analysis Based on Local Mean Decomposition and Its Application to Gear Fault Diagnosis[J].China Mechanical Engineering,2011,22(14):1731-1736.

[5]Colas M,Gelle G.Blind Source Separation:A Tool for Rotating Machine Monitoring by Vibration Analysis[J].Sound and Vibration,2001,248(5):865-885.

[6]程军圣,郑近德,杨宇.一种新的非平稳信号分析方法-局部特征尺度分解[J].振动工程学报,2012,25(2):215-220.

Cheng Junsheng,Zheng Jinde,Yang Yu.A Nonstationary Signal Analysis Approach—the Local Characteristic-scale Decomposition Method[J].Journal of Vibration Engineering,2012,25(2):215-220.

[7]杨宇,曾鸣,程军圣.基于局部特征尺度分解和核最近邻凸包分类算法的滚动轴承故障诊断方法[J].振动工程学报,2013,26(1):118-126.

Yang Yu,Zeng Ming,Cheng Junsheng.Fault Diagnosis Approach for Rolling Bearing Based on Local Characteristic-scale Decomposition and Kernel Nearest Neighbor Convex Hull Classification Algorithm[J].Journal of Vibration Engineering,2013,26(1):118-126.

[8]Minka T P.Automatic Choice of Dimensionality for PCA[J].Advances in Neural Information Processing Systems,2001,13:598-604.

[9]Cardoso J F,Souloumiac A.Blind Beamforming for Non-Gaussian Signals[J].Radar and Signal Processing,IEE Proceedings F,1993,140(6):362-370.

(编辑张洋)

BSS Method of Gearbox Multi-fault Based on LCD

Yang YuLi YongguoHe ZhiyiCheng Junsheng

State key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University,Changsha,410082

BSS is an effective multi-fault diagnosis method,and LCD is an effective tool of analyzing and processing non-stationary signals.Combining the advantages of LCD and BSS,a BSS of gearbox multi-fault was proposed based on LCD.The source signals were decomposed by LCD to constitute new multidimensional signals,then estimating blind source number by Bayesian information criterion(BIC) to restructure the multidimensional signals,finally,using joint approximate diagonalization to separate the blind source signals.Simulation and experiments show that the method can effectively separate the blind source of the gearbox multi-faults,and provide a new method for fault diagnosis of the gearbox.

blind source separation(BSS);local characteristic scale decomposition(LCD);gearbox;fault diagnosis

2014-05-19

国家自然科学基金资助项目(51175158,51375152);湖南省自然科学基金资助项目(11JJ2026)

TH113DOI：10.3969/j.issn.1004-132X.2015.08.013

杨宇,女,1971年生。湖南大学机械与运载工程学院教授、博士研究生导师。主要研究方向为动态信号处理、机电设备状态监控与故障诊断、模式识别等。发表论文60余篇。李永国,男,1988年生。湖南大学机械与运载工程学院硕士研究生。何知义,男,1990年生。湖南大学机械与运载工程学院硕士研究生。程军圣,男,1968年生。湖南大学机械与运载工程学院教授、博士研究生导师。