基于改进殖民竞争算法的最小碰集求解

朱传军　曹　静　张超勇　连坤雷

1.湖北工业大学，武汉，4300682.华中科技大学数字制造装备与技术国家重点实验室，武汉，430074

基于改进殖民竞争算法的最小碰集求解

朱传军1曹静1张超勇2连坤雷2

1.湖北工业大学，武汉，4300682.华中科技大学数字制造装备与技术国家重点实验室，武汉，430074

利用改进殖民竞争算法生成企业设备的最小候选集，其最小候选集就是企业设备的最小碰集。在对殖民竞争算法进行深入研究的基础上，引入自由国家的概念，同时对算法流程中帝国初始化阶段和帝国内同化及更新阶段进行改进，提高了算法效率。与DMDSE-Tree算法进行了对比，在计算90%的最小碰集时，改进殖民竞争算法具有良好的效率。最后，通过某企业实例对算法的有效性进行了验证。实验结果表明，该方法能有效应用于企业设备选择组合优化问题的求解。

企业规划；殖民竞争算法；最小碰集；设备选择

0　引言

在现实生活中有很多问题可以转化为与集合族的每个集合交集为非空的最小集合，即最小碰集问题，如基于模型的诊断中从最小冲突集生成诊断、在基因表达式分析中寻找解释基因特性的片段问题、集体用户公费购买书籍时的决策问题等都可以通过计算最小碰集而得到解决。计算最小碰集问题是一个NP难问题，研究者一直在寻找提高求解最小碰集效率的方法。Reiter[1]在基于模型诊断中最早提出计算最小碰集的方法——HS-Tree方法，由于该方法在求解过程中加入剪枝策略和关闭策略，故该方法会丢失正确解。为了保证求解出所有的最小碰集，Greiner等[2]对文献[1]方法进行了改进，给出了结合非循环图的HS-DAG方法。至今，国内外已有许多学者对求解最小碰集问题进行了研究和改进，提出了许多求解方法，主要包括精确求解和近似求解方法。精确求解方法有：基于BNB-HSSE的算法[3]、基于CHS树和递归布尔算法的组合算法[4]、HSSE树和二元标记组合算法[5]、分枝缩减方法[6]和基于动态极大度的最小碰集求解方法(DMDSE-Tree)[7]。对于规模很大的复杂系统，精确方法在时间和空间上仍然不符合工程实际问题的需求，而且求解复杂系统完全意义上的最优解也没有太大的现实意义。因此，一些学者提出了最小碰集的近似求解方法，如离散粒子群算法[8]、二进制粒子群优化算法[9]和采用启发式函数的低成本近似最小碰集算法STACCATO[10]等。

Atashpaz-Gargari等[11]通过模拟人类社会发展中殖民竞争过程，提出了殖民竞争算法(colonial competitive algorithm,CCA)，它是基于群体的元启发式算法，比遗传算法与粒子群优化算法具有更好的收敛性，近年来得到了越来越广泛的应用。例如，Forouharfard等[12]将殖民竞争算法应用于求解中转库的物流计划问题；Kaveh等[13]将殖民竞争算法应用于结构最优化设计；Nazari等[14]将殖民竞争算法用于混流生产中的产品外包问题；Sarayloo等[15]用殖民竞争算法解决动态单元化制造问题。此外，学者们还对殖民竞争算法进行了一些改进，并将其应用于解决组合优化问题[16]、多产品混流装配线平衡问题[17]和数据聚类问题[18]。本文运用改进殖民竞争算法研究近似求解最小碰集问题，并通过企业设备选择的组合优化问题验证了算法的有效性。

1　改进的殖民竞争算法求解最小碰集问题

在深入研究殖民竞争算法的基础上，本文提出了一种改进的殖民竞争算法，其核心在于引入自由国家的概念。殖民竞争算法中两个重要的国家类型是殖民国家和殖民地，事实上还存在第三种国家——自由国家。这三类国家在改进的殖民竞争算法中的功能定义如下：

(1)殖民国家。殖民国家都尽力同化它的殖民地，并且尽力占有越来越多殖民地。

(2)殖民地。殖民地都尽力向殖民国家学习，争取成为殖民国家或者自由国家。

(3)自由国家。自由国家都尽力向殖民国家学习，并努力成为殖民国家。

改进殖民竞争算法与原始的殖民竞争算法的主要区别在于帝国初始化阶段、帝国内同化和更新阶段，这是因为这些阶段中增加了自由国家的算法操作。

1.1帝国初始化

改进殖民竞争算法中的初始群体有三类国家：殖民国家、殖民地和自由国家，其参数包括Nimp、Ncol和Nind，分别为三类国家的数量。因此，算法初始化阶段国家总数Npop=Nimp+Nind+Ncol。对群体初始化后，按算法参数首先挑选出Nimp个殖民国家和Ncol个殖民地，其余种群数就是Nind个自由国家。构造帝国的方法与原始的殖民竞争算法相同，自由国家不受所有的帝国影响，因此帝国中不包含任何自由国家。算法初始化阶段国家的分类如图1所示。

1.2算法编码

编码是运用殖民竞争算法求解遇到的首要问题，也是应用成功与否的关键问题。二进制编码是最常用的编码方式，运算较易于实现。

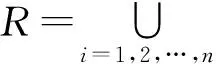
为保证初始群体中的个体接近最小碰集，减少进化的代数，并且减小极小化操作的运算量，初始群体中个体元素个数的平均值(即染色体中基因为“1”的基因数的平均值)约为最小碰集中元素的个数的平均值。设X为最小碰集中元素的平均个数，基因取“1”的概率为β，则

β=X/N

(1)

一般情况下，X是未知的，所以只能估计β的取值。根据经验，β取值应为0.1～0.5。当集合个数n变大时，β取值也相应变大。

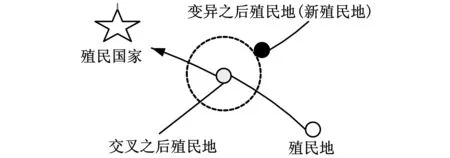
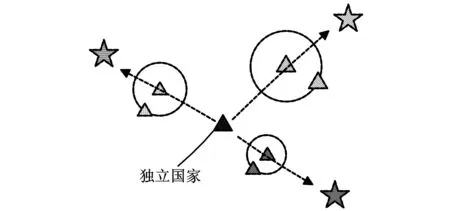
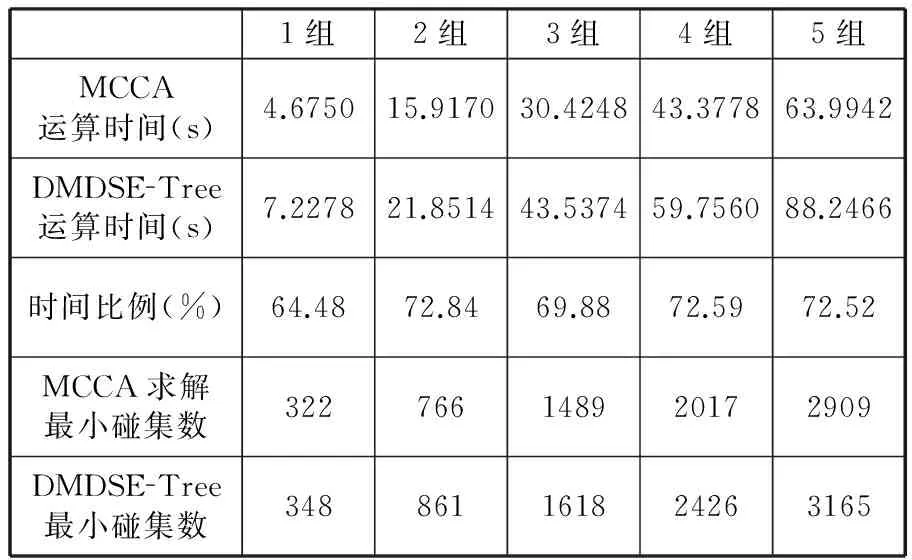
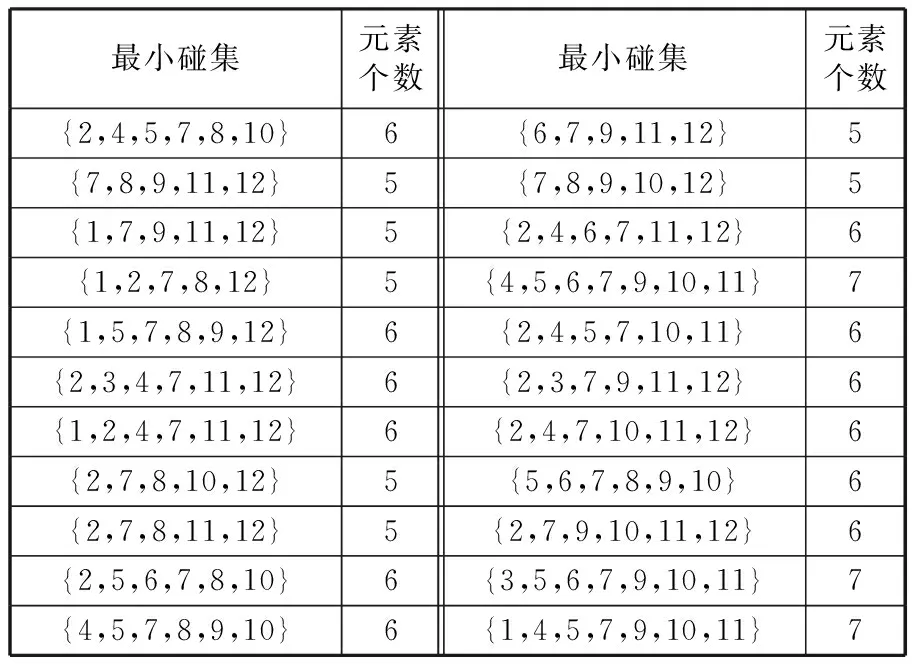
设染色体为Y，染色体上的i(i

1.3评价适应度

适应度函数是殖民竞争算法的核心，它的优劣直接关系到算法搜索的效率。适应度是表示某一个体相对于目标函数的优劣程度，在算法中还用来确定该个体繁殖后代能力的大小。适应度函数也称为评价函数，是用来判断群体中的个体的优劣程度的指标，它一般根据所求问题的目标函数来进行评估。

对群体中每一个体指定一个适应度的值，要根据问题求解的实际接近程度来确定。对于最小碰集的求解，有以下两个必要条件：①它是碰集；②它的任意真子集都不能是碰集。本文中采用的适应度函数为f(x)=t。其中，t表示当前个体与集合族中集合有非空交集的集合个数。集合的任意真子集是否为碰集，与集合中元素的个数没有直接关系，这里无法表示出来。根据适应度函数算法收敛于碰集，而不是最小碰集，这就需要将求得的碰集转化为最小碰集。

1.4极小化操作

本文加入极小化操作的目的就是将得到的超集转化为对应的最小碰集。其方法就是将个体中基因为“1”的位置变为“0”再求其适应度，若适应度不变，则保留变化，直至对所有的基因为“1”的位置执行上述操作，个体就变成了最小碰集。

在个体中基因为“1”的位置大多数是相互关联的，即该位置上的“1”是否能转化为“0”与其他位置上的“1”是否转化为“0”有关。这要根据吸收后的集合中元素对应的位置，如果吸收后的集合中含有2个或2个以上的元素，则这些元素是关联的，否则就不是关联的。

如果从首位开始扫描基因串，就会发现基因串中前面的“1”转化为“0”的概率比后面的“1”大，则基因串后面的基因位所代表的个体比前面的基因位所代表的个体更容易出现在最小碰集中。为了使含有基因串前面位置所代表元素的最小碰集出现的概率与其他最小碰集出现的概率基本相同，应采用一种随机性的扫描方法来将超集转化为最小碰集。

极小化操作的主要过程如下：

(1)当前操作的对象是否为碰集，若是则转步骤(2)，否则保持原状。

(2)从第k(k为随机取值且k

1.5殖民竞争

与殖民竞争算法相同，改进殖民竞争算法中的殖民竞争首先要计算各个帝国的总能量，一个帝国的总能量由其中的殖民国家和所有的殖民地的能量来确定，计算公式如下：

ECn=Jn+α×mean{Jm}

(2)

其中，ECn是第n个帝国的总能量；α∈(0,1)，用来平衡殖民国家能量在整个帝国能量中占的比重，即α越大，殖民国家能量占的比重越小，反之就越大，通常情况下α=0.1。Jn是殖民国家的能量，Jm是第n个帝国中第m个殖民地的能量。

与殖民竞争算法相同的是，改进的殖民竞争算法中每个帝国都努力地占有更多的殖民地，从而增加自己的总能量。殖民竞争过程会使有些帝国占有越来越多的殖民地，这样必然使其他帝国逐渐减少所占有的殖民地。其竞争过程实现如下：首先，找出当前能量最小帝国内的最弱殖民地，将该殖民地设为自由状态；然后，所有帝国通过竞争来取得对该自由状态殖民地的占有权。不同帝国对自由状态殖民地的占有由一定的概率来决定，即最强的帝国以最大的概率来占有该殖民地。

竞争过程需要计算不同帝国占有自由状态殖民地的概率，为此需要求出各帝国的标准化之后的总能量ECNn：

(3)

其中，ECn和ECNn分别表示帝国的总能量和标准化之后的总能量。由此可求得各帝国对自由状态殖民地的占有概率Pn:

(4)

为了将自由殖民地分配给殖民国家，构造如下向量：

P=(p1,p2,…,pNimp)

(5)

然后构造一个与P同样大小的由均匀分布随机数组成的向量R:

R=(r1,r2,…,rNimp)r1,r2,…,rNimp∈U(0,1)

(6)

通过下列运算得到向量D:

D=P-R=(D1,D2,…,DNimp)=

(p1-r1,p2-r2,…,pNimp-rNimp)

(7)

通过以上运算，自由状态的殖民地将被D值最大的帝国占有。殖民竞争过程如图2所示。

图2　殖民竞争过程示意图

1.6算法同化过程

在改进殖民竞争算法中，同化分为两种情况，即帝国内同化和殖民国家与自由国家之间的同化。帝国内同化只涉及殖民国家与殖民地，而与自由国家无关。殖民国家与自由国家之间的同化过程主要包括以下步骤：

(1)每个自由国家首先向所有殖民国家移动，移动过程与殖民地向殖民国家移动步骤相同，通过交叉和变异来实现。本文采用单点交叉运算，随机产生的变异点，对其基因值取反运算，即将基因值由“1”改为“0”或由“0”改为“1”，产生一个崭新的个体。

(2)每个自由国家在向每个殖民国家移动之后，会得到一个新的自由国家。对这些新的自由国家进行比较，选择最优的自由国家作为其移动的最终位置。

帝国内同化和殖民国家与自由国家之间同化过程如图3所示。可以看出，帝国内同化发生在殖民国家和它的所有殖民地之间，而殖民国家和自由国家之间的同化发生在每个自由国家和所有殖民国家之间。自由国家在做出最终移动之前，都会向每个殖民国家做出虚拟的移动，在确定最优移动位置之后才完成真实的移动。这样能加快算法的收敛，但是增加了算法的步骤，从而增加了计算时间。

(a)帝国内同化过程

(b)殖民国家与自由国家之间的同化过程图3　改进算法同化过程

1.7更新过程

改进殖民竞争算法的更新过程有以下三类：

(1)殖民国家与殖民地之间的更新。如果帝国内同化之后新殖民地比殖民国家更优，新殖民地就变成殖民国家，如图4a所示。

(2)自由国家与殖民国家之间的更新。如果最强的自由国家在更新之后比最弱的殖民国家更优，该自由国家与殖民国家互换，如图4b所示。

(a)殖民国家与殖民地之间的更新

(b)自由国家与殖民国家之间的更新

(c)殖民地与自由国家之间的更新图4　更新过程示意图

(3)殖民地与自由国家之间的更新。在所有更新完成之后，如果最强的殖民地比最弱的自由国家更优，该该殖民地与自由国家互换，如图4c所示。 1.8帝国删除

改进的殖民竞争算法中帝国删除步骤与基本殖民竞争算法相同。

2　实验结果分析

随机生成50个数组，每个数组元素为10个，每个元素小于或等于20，将每个数组从小到大排序，相等的数用0代替，得到数组。将这50个数组分成小、中、大规模共5组，第1组为数组1～10，第2组为数组1～20，…，第5组为数组1～50。分别用改进的殖民竞争算法(MCCA)和基于动态极大度的极小碰集求解方法(DMDSE-Tree)[7]求解5组数据的最小碰集数和每组数据5次运算的平均运算时间。比较两种方法求解5组数据的最小碰集数和平均运算时间。

试验计算机配置如下:CPU为Intel Pentium G630 2.70 GHz，内存为2 GB, 操作系统为Windows XP，程序使用Visual C++ 6.0编写。改进的殖民竞争算法参数设置如下：Npop=100，Nimp=7，Nind=5, 最大迭代次数Nmax=100，权重分别取0.2,0.3,…,0.8，测试α=0.6结果最优。DMDSE-Tree和MCCA算法求得的最小碰集数和运算时间见表1和表2。

表1　DMDSE-Tree求解最小碰集数和平均运算时间表

表2　MCCA求解最小碰集数和平均运算时间表

统计5组数据在两种方法下的平均运算时间与求解最小碰集数，并计算时间比例和求解比例，结果见表3。

表3　对比数据表

从表3可以看出，在MCCA求解约90%的最小碰集的情况下，MCCA的运行时间要比DMDSE-Tree的运行时间短。虽然MCCA只求解了约90%的最小碰集，但它只用了DMDSE-Tree算法时间的70%左右。可见，在求解部分最小碰集时，改进殖民竞争算法的质量与效率要优于DMDSE-Tree算法。同时，本文随机生成50个数组数据，分别对小、中、大规模进行求解，均获得较优结果，说明本文算法具有较高的鲁棒性。

3　设备选择组合优化中的应用

某企业采用模块式生产方式，现有12个制造单元，分别用A,B,…,L来表示，每个制造单元由多台通用机床组成。企业将推出一种新产品P1，P1中自制零件有23个。由于产品的批量较小且机床有足够的生产能力，多个零件可以在同一个制造单元内完成。为使新增产品对现有的生产计划产生较小的影响，应采用最少的制造单元来完成这批产品。自制零件所对应的制造单元见表4。

表4　零件所对应的制造单元表

采用改进殖民竞争算法求解最小碰集的方法来得到最少的制造单元组，其具体步骤如下：

(1)将制造单元用数字编号，A为1，B为2，C为3，…，L为12，将零件对应的制造单元用数字编号代替。取零件对应的制造单元个数为5(制造单元个数的最大值)，不足的制造单元用“0”表示，生成一个输入文件。

(2)用改进的殖民竞争算法的C++语言程序计算最小碰集，算法参数设置如下：Npop=100，Nimp=7，Nind=5, 最大迭代次数Nmax=100，权重取0.6。其计算结果与分析见表5。

表5　计算结果与分析

元素个数最少的最小碰集为：{7，8，9，11，12}，{1，7，9，11，12}，{1，2，7，8，12}、{2，7，8，10，12}，{2，7，8，11，12}，{6，7，9，11，12}，{7，8，9，10，12}。

(3)将元素个数最少的最小碰集转换为制造单元组：{G,H,I,K,L}，{A,G,I,K,L}，{A,B,G,H,L}、{B,G,H,J,L}，{B,G,H,K,L}，{F,G,I,K,L}，{G,H,I,J,L}。

若采用上述制造单元组来加工产品P1，则其他的制造单元就不用改变生产计划，只需要调整这5个制造单元的生产计划，而且在制品的数量较小。当批量发生改变时，批量变更所产生的调整费用也较小。

4　结束语

碰集求解在工程实际中具有很多应用，但它具有计算复杂性。本文针对该问题的组合优化特性，提出了殖民竞争算法来寻找最优解或近优解。在对殖民竞争算法进行深入研究的基础上，提出了改进的殖民竞争算法，详细介绍了算法的实施流程和操作步骤。为了验证算法性能，本文进行了一系列的测试，该算法虽不能保证求出全部的最小碰集，但能够在可接受的时间内给出绝大部分的最小碰集，并且保证了输出的结果都是最小碰集。为了保证结果都是不相同的最小碰集，在运算过程中要进行大量的比较，减缓最小碰集求解速度。最后，将最小碰集应用于企业的设备选择的组合优化问题中。

[1]Reiter R.A Theory of Diagnosis from First Principles [J].Artificial Intelligence,1987,32(1):57-96.

[2]Greiner R,Smith B A,Wilkerson R W.A Correction to the Algorithm in Reiter’s Theory of Diagnosis(Research Note)[J].Artificial Intelligence, 1989, 41(1):79-88.

[3]陈晓梅，孟晓风，乔仁晓.基于BNB-HSSE计算全体碰集的方法[J].仪器仪表学报，2010，31(1)：605-608.

Chen Xiaomei,Meng Xiaofeng,Qiao Renxiao.Method of Computing All Minimal Hitting Set Based on BNB-HSSE [J].Chinese Journal of Scientific Instrument,2010,31(1):605-608.

[4]Wang Ziling, Xu Aiqiang, Wang Dingguo,et al.Research on a New Combined Algorithm for Computing Minimal Hitting Sets[C]//Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation.Changsha,2010: 14-17.

[5]Feng Wenquan, Du Min, Zhao Qi, et al.A Method of Combining HSSE-tree and Binary Label to Compute All Minimal Hitting Sets[C]//2011 Fourth International Symposium on Computational Intelligence and Design.Hangzhou,2011:14-17.

[6]Shi Lei,Cai Xuan.An Exact Fast Algorithm for Minimum Hitting Set[C]//2010 Third International Joint Conference on Computational Science and Optimization.Huangshan, 2010: 64-67.

[7]张立明,欧阳丹彤,曾海林.基于动态极大度的极小碰集求解方法[J].计算机研究与发展,2011,48(2)：209-215.

Zhang Liming, Ouyang Dantong,Zeng Hailin.Computing the Minimal Hitting Sets Based on Dynamic Maximum Degree[J].Journal of Computer Research and Development,2011,48( 2):209-215.

[8]蒋荣华,田书林,龙兵.基于DPSO的最小碰集算法的掩盖故障识别[J].系统工程与电子技术,2009,31(4):997-1001.

Jiang Ronghua,Tian Shulin,Long Bing.Minimal Hitting Sets Algorithm of Identifying Masking False Failure Sets Based on DPSO[J].Systems Engineering and Electronics,2009,31(4):997-1001.

[9]吕晓明，黄考利，连光耀.基于BPSO的多故障最小候选集生成技术[J].系统工程与电子技术, 2012,34(5):961-965.

Lü Xiaoming, Huang Kaoli, Lian Guangyao.Generation of Minimal Candidate Set for Multiple Fault Diagnosis Based on Binary Particle Swarm Optimization[J].Systems Engineering and Electronics,2012,34(5):961-965.

[10]Abreu R,van Gemund A J C.A Low-cost Approximate Minimal Hitting Set Algorithm and Its Application to Model-Based Diagnosis[C]//Proceedings of the 8th Symposium on Abstraction,Reformulation and Approximation.Lake Arrowhead,2009:2-8.

[11]Atashpaz-Gargari E,Lucas C.Imperialist Competitive Algorithm: an Algorithm for Optimization Inspired by Imperialistic Competition[C]//IEEE Congress on Evolutionary Computation.Singapore,2007:4661-4667.

[12]Forouharfard S, Zandieh M.An Imperialist Competitive Algorithm to Schedule of Receiving and Shipping Trucks in Cross-docking Systems[J].The International Journal of Advanced Manufacturing Technology,2010,51(9):1179-1193.

[13]Kaveh A,Talatahari S.Optimum Design of Skeletal Structures Using Imperialist Competitive Algorithm[J].Computers&Structures,2010,88 (21/22):1220-1229.

[14]Nazari-Shirkouhi S,Eivazy H,Ghodsi R,et al.Solving the Integrated Product Mix-outsourcing Problem Using the Imperialist Competitive Algorithm[J].Expert Systems with Applications,2010,37(12):7615-7626.

[15]Sarayloo F,Tavakkoli-Moghaddam R.Imperialistic Competitive Algorithm for Solving a Dynamic Cell Formation Problem with Production Planning[J].Advanced Intelligent Computing Theories and Applications,2010,6215:266-276.

[16]Hadji M M,Vahidi B.A Solution to the Unit Commitment Problem Using Imperialistic Competition Algorithm[J].IEEE Transactions on Power Systems, 2011, 27(1):117-124.

[17]Bagher M,Zandieh M,Farsijani H.Balancing of Stochastic U-type Assembly Lines:an Imperialist Competitive Algorithm[J].The International Journal of Advanced Manufacturing Technology,2011,54(1/4):271-285.

[18]Niknam T,Fard E T,Pourjafarian N,et al.An Efficient Hybrid Algorithm Based on Modified Imperialist Competitive Algorithm and K-means for Data Clustering[J].Engineering Applications of Artificial Intelligence,2011,24 (2):306-317.

(编辑陈勇)

Applying Modified Colonial Competitive Algorithm to Solve Minimal Hitting Set Problems

Zhu Chuanjun1Cao Jing1Zhang Chaoyong2Lian Kunlei2

1.Hubei University of Technology,Wuhan，430068 2.State Key Laboratory of Digital Manufacturing Equipment & Technology，Huazhong University of Science and Technology,Wuhan，430074

A CCA was developed and modified to solve the problem of minimal candidates set.The minimal candidate set was a minimal hitting set. The modified CCA improved performance in initialization, assimilation and rebirth of original CCA by introducing a third type of country, independent country,to the population of countries maintained by CCA.Implementation details of the proposed CCA and modified colonial competitive algorithm(MCCA) were elaborated using an illustrative example.The performance of the algorithms was analyzed,and the results by the MCCA were compared with DMDSE-Tree algorithm.When 90% of the minimal hitting sets are obtained, the MCCA has better efficiency. Finally, the experimental results of certain system verify the effectiveness of the algorithm,which proves that this method can be applied in solving the minimal hitting set of combinatorial optimization problems for selection of equipment effectively.

business planning; colonial competitive algorithm(CCA); minimal hitting set; equipment selection

2014-03-11

国家自然科学基金资助重点项目(51035001)；国家自然科学基金资助项目(51275190)；湖北省自然科学基金资助项目(2012FFB0063，2013CFB025)

TB114.1DOI：10.3969/j.issn.1004-132X.2015.07.011

朱传军，男，1971年生。湖北工业大学机械工程学院副教授、博士。主要研究方向为智能优化算法、决策分析。曹静，女，1970年生。湖北工业大学机械工程学院讲师。张超勇，男，1972年生。华中科技大学数字制造装备与技术国家重点实验室副教授、博士。连坤雷，男，1987年生。华中科技大学数字制造装备与技术国家重点实验室硕士研究生。