基于牛顿迭代法的S形加减速时间算法研究

杨亮亮　许守金　史伟民　葛宏伟

1.浙江省现代纺织装备技术重点实验室,杭州,3100182.浙江理工大学,杭州,310018

基于牛顿迭代法的S形加减速时间算法研究

杨亮亮1,2许守金1,2史伟民1,2葛宏伟1,2

1.浙江省现代纺织装备技术重点实验室,杭州,3100182.浙江理工大学,杭州,310018

S形加减速控制涉及求解多元高次方程或者不等式，且要求求解出来的最终解是非负数，为此根据时间最优原则和速度、加速度的限制条件，把S形加减速控制中所涉及的五元非线性方程组分解为2个二元非线性方程组和1个一元线性方程。采用牛顿迭代法和迭代修正的方式逐步求解出符合要求的加减速时间，进而求出速度曲线，进行插补运算。仿真与实验结果证明,该算法简明高效、运行稳定，能够满足高速高精数控要求。

S形加减速控制;五元非线性方程;牛顿迭代法;时间最优原则

0　引言

数控机床的进给速度与加工精度、生产率以及工件表面粗糙度有着密切关系,因此进给速度应该稳定、可靠[1]。现在较为流行的加减速控制是S形加减速控制,相比直线型加减速和指数型加减速控制,S形加减速控制有速度曲线光滑、均匀、运动平稳、无冲击等优势[2]。S形加减速控制能较好地实现机床各轴的平滑启停和速度切换，可做到无加速的突变，能够较好地减小机床的运动冲击和振荡,从而有效提高工件的加工质量，特别适用于高速高精加工[3]。

一般的S形速度曲线是关于时间的多项式，其位移曲线的最大阶次可以是3、4、5。高阶的曲线可以获得高阶的连续导数，但计算量也会更大[4]。应用中,大于3阶的位移曲线对加工精度影响不明显，实际上最为常用的是限制加加速度的2阶S形速度曲线即3阶位移曲线。一般情况下，始末速度不为零的S形加减速曲线包含5个时间未知量，加速度曲线最多会有十几种变化情形[5],又涉及多元非线性方程，计算比较繁琐，没有统一的公式解法。在加减速时间规划中，这5个时间未知量不能为负数，这使得求解S形加减速控制的各阶段时间尤为复杂[6]。

穆海华等[7]研究了点对点运动三阶轨迹轮廓可能存在的情形并建立三个约束基准用来预判以上情形，给出了一种三阶点对点轨迹规划的通用算法。该算法处理了实际应用中存在的各种情形，具有极强的灵活性和可靠性，但这种规划方法加减速模式分类复杂、运算繁琐、不易理解。郭新贵等[8]研究了一种柔性加减速算法，采用三角函数构造加减速曲线，从而使得机床运行具有柔性。虽然三角函数加减速规律可以实现平滑运动，由于三角函数的计算复杂，需要事先对其进行处理，并且要将其作为样板以数表的形式存放于内存，通过查表的方式实现，这给实际应用带来了诸多不便。徐瑞民[9]总结了利用牛顿迭代法求解二元非线性方程组根的计算方法，并通过软件仿真验证该算法的可行性，但是该算法只是针对数学问题，没有考虑怎么求得非负数的收敛值，因此不能完全适用于运动控制领域。

为此,本文根据时间最优原则并考虑速度、加速度限制的S形加减速时间算法，把S形加减速控制中所涉及的五元非线性方程组分解为2个二元非线性方程组和1个一元线性方程，采用牛顿迭代法和迭代修正的方式逐步求解出符合要求的加减速时间，进而求出速度曲线，进行插补运算。

1　S形加减速时间规划算法

图1中,tj1为加加速时间(减加速时间),ta1为匀加速时间,tv1为匀速时间,tj2为加减速时间(减减速时间),ta2为匀减速时间。

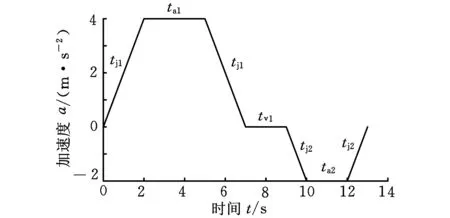
图1　完整的加速度变化曲线

始末速度不为零的S形加减速控制包含7个速度变化段：加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段。其中，加加速段与减加速段的时间相同，加减速段与减减速段的时间相同。始末速度与加减速时间的关系为

(1)

式中,j为加加速度;vs为初始速度;ve为末速度。

位移s与加减速时间的关系为

(2)

1.1时间最优化下的加速度变化时间

式(1)、式(2)有5个未知量,但是只有2个方程，直接根据方程无法得到确切的加减速时间。从实际情况考虑，总是希望在满足加工精度要求下，最大限度地提高生产率。根据经验可知，一段位移如果想在最短的时间内移动完毕，不考虑限制因素，它的移动方案应该是从开始一直以最大的加速度进行加速移动，移动一段时间后，再以最大的加速度进行减速移动，到达终点时恰好速度减为零，这种移动方案用时最短，这种满足最高效率的算法称为时间最优算法[10]。用到数控机床上就是只有加加速段、减加速段、加减速段和减减速段,不存在其他速度变化段,加速度变化如图2所示。考虑到机床系统的动力学因素，这种加工模式无法实现[11],但是可以先求出加速度的变化时间，再考虑限制条件。因此先令ta1=ta2=tv1=0,求tj1、tj2值。

图2　不考虑加速度、速度限制的加速度变化曲线

由式(1)、式(2)可得关于速度和位移的二元三次方程组：

(3)

1.1.1加速度变化时间的牛顿迭代算法

无法通过现成的公式得到二元三次方程组的准确解，但可采用牛顿迭代法求出它的收敛值,进而求出方程组的解,首先把式(3)构造成2个函数：

(4)

(5)

求式(4)、式(5)的一阶偏导数并构成矩阵A：

(6)

求得偏导数矩阵A的逆矩阵A-1,计算tj1、tj2的迭代初值。好的迭代初值能加快收敛，节省计算时间,由于tj1、tj2在很多情形下相差不大,且迭代初值也不需要太精确,因此把tj1、tj2看作相等的值tj,根据式(3)可得tj计算公式：

再把tj赋值给tj10、tj20后,并代入式(4)～式(6)计算出第一次迭代值tj11、tj21：

(7)

式中,tj10为tj1的迭代初值;tj20为tj2的代初值;tj1 i、tj2 i分别为tj1、tj2第i次迭代值。

利用计算出的迭代值计算迭代精度:

P=(tj11-tj10)2+(tj21-tj20)2

(8)

判断精度是否满足要求,如果不满足则把计算出的tj11、tj21值作为迭代值,代入式(4)～式(8)进行第二次迭代计算。反复进行迭代计算，直到计算出满足精度要求的迭代值。如果迭代始终无法收敛，则迭代次数达到设定值就停止迭代，进行后面的计算。

加减速控制涉及的是时间分配问题，如果最终收敛值是一组负数解，考虑到关于始末速度和位移所组成的方程组的复杂性，此时取最接近收敛值的一组正数解作为方程组的最终解。通过上述过程就能得到初步满足要求的tj1、tj2。

1.1.2加速度变化时间的迭代修正

速度、加速度必须满足机械系统动力学约束条件，即需要考虑速度、加速度的限制条件。首先考虑速度约束，由于最大速度出现在减加速段结束时，因此根据牛顿迭代法求出的收敛值必须与所允许的最长加速度时间进行对比，取其中的较小值作为tj1，计算公式如下：

再考虑加速度约束要求,加速度最大值出现在加加速度段结束时，根据前面求出的tj1的值必须满足加速度的约束要求，与机械系统所允许的最长加速时间进行对比，取其中的较小值，计算公式如下：

tj1←min(tj1,am/j)

由式(3)可得,tj1改变时,相应地tj2也需要重新计算，计算公式如下：

把tj2与允许的最长加速度时间进行对比,取其中的较小值,计算公式如下：

tj2←min(tj2,am/j)

这样就求出满足速度和加速度限制要求的tj1、tj2。

用迭代法求出的最优解存在误差,为了减小误差,提高准确度，需要根据始末速度限制条件和位移限制条件对求出的tj1、tj2再次进行迭代修正。考虑到计算出的时间必须满足加速度和速度的限制要求,则进行第二次迭代修正时，时间值tj1、tj2只能减少不能增加。速度误差Pv的计算公式如下：

(9)

设定精度Pv>P说明tj1取得值较大,tj1相应地减少一个伺服周期Ts后,再代入式(9)进行计算比较,如果还不满足要求，则继续减少，一直减少到满足要求为止。如果tj1减到零时也无法满足要求,则退出循环。Pv<-P说明tj2取得值较大，tj2相应地减少一个伺服周期Ts后,再代入式(9)进行计算比较,一直减少到满足要求为止,如果tj2减到零时也无法满足要求,则退出循环。

根据位移限制条件进行判断,对求出的tj1、tj2,进行迭代修正。计算公式如下：

(10)

其中,Ps为根据规划的时间计算得到的位移值和实际位移值之差。Ps>0说明规划出来的轨迹长度大于实际的长度,这不符合要求,必须减少规划的时间，tj1应减少一个伺服周期，tj2相应地也要改变,由式(3)可得tj2的计算公式：

把重新计算得到tj1、tj2代入式(10),计算位移误差Ps并进行比较，如果不满足要求则重复此过程。Ps<0说明按照tj1、tj2进行轨迹规划的位移量小于实际的位移，则结束迭代修正过程。

通过牛顿迭代和迭代修正的方法就求出了满足要求、误差减到最小的tj1、tj2。

1.2最优时间下的匀加速时间

通过式(10)可知，最终求出的tj1、tj2能满足速度和加速度的限制要求,但一般无法运行完期望规划的轨迹长度,即只有加加速段、减加速段、加减速段、减减速段的S形加减速控制无法满足所需要位移要求,S形加减速控制还存在匀加速段、匀减速段和匀速段，根据时间最优原则令tv1=0,此时S形加减速控制的加速度变化如图3所示。由式(1)、式(2)可得关于始末速度和位移限制方程组：

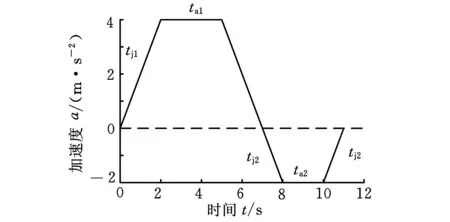
图3　不考虑匀速段的加速度变化示意图

根据1.1节中的牛顿迭代和迭代修正理论可以求出满足要求、误差减到最小的ta1、ta2。

1.3最优时间下的匀速时间

S形加减速控制涉及7个速度变化段、5个时间量，通过上述过程，4个满足要求的时间参数tj1、tj2、ta1、ta2已经求出,关于tv1的方程是一元一次方程，必有一个解。由位移与加减速时间的关系方程(式(2))可得关于tv1的方程：

(11)

通过式(11)可以求出tv1。至此,一段轨迹的加减速变化时间都已经求出，根据加减速变化时间，可以得到此轨迹的速度曲线。根据求出的速度曲线以及起始点，进行插补运算计算出中间点的坐标值，根据坐标值变化向相应坐标输出脉冲信号，控制各执行元件的进给速度、进给方向和进给位移量等，进而完成工件的加工任务。

2　实例与分析

2.1对运算速度进行验证

为验证本论文算法的运算速度,用MATLAB进行编程仿真,编程思路如图4所示。给定限制条件：起始速度vs=0.06 m/s,末速度ve=0.03 m/s,加加速度j=25 m/s3,伺服周期Ts=1 ms,最大限制加速度am=5 m/s2,最大限制速度vm=0.8 m/s,把位移量作为唯一变量,位移量s从0.005 m到500 m进行等间距取值,统计取不同的位移值时MATLAB软件仿真完成所需要的时间,仿真结果如图5所示。

图4　S形加减速控制时间计算流程图

图5　仿真运算时间随着位移变化曲线

通过图5可以看出,位移s=0.05 m时所需要的运算时间最短,随着位移的增加,求解时间都小于1 ms,这说明本文算法够满足高速的加工要求，能有效提高数控系统的稳定性和效率。

2.2对轨迹规划精度进行验证

上述实例没有对本算法的轨迹规划精度进行考虑，为了进一步验证本算法的可行性，在自行开发的“计算机+运动控制卡”架构的直线伺服系统上运行图6所示的样条曲线,直线伺服系统为2个直线电动机构成的X-Y运动平台,2个直线电动机均为Baldor公司的LMCF02C-HCO,伺服驱动器为Baldor公司的FMH2A03TR-EN23。把本算法编进运动控制卡中进行插补控制,直线伺服系统平台如图7所示。

图6　样条曲线

图7　直线伺服系统试验台

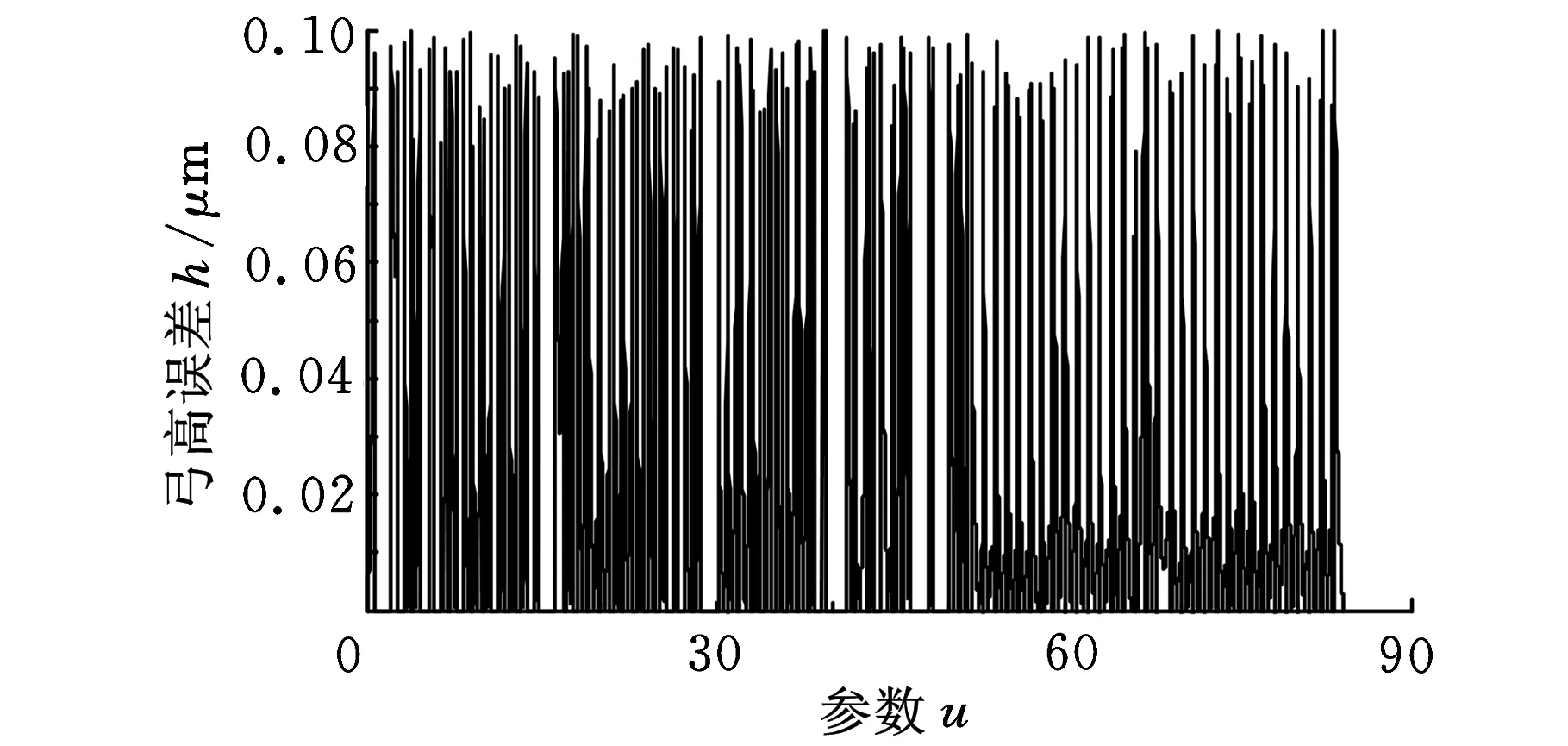
图8　弓高误差效果图

图9　加速度变化图

图10　速度变化图

给定限制条件：加加速度j=25 m/s3,伺服周期Ts=1 ms，最大限制加速度am=5 m/s2,最大限制速度vm=0.8 m/s，允许的弓高误差为0.1 μm，采用周期为1 ms。最终运行的弓高误差效果如图8所示，加速度、速度随着插补时间变化如图9、图10所示，可以看出本算法能完全满足加工精度的要求。

3　结论

(1)本文提出了一种S形加减速时间计算方法，根据时间最优原则以及加速度、速度限制条件，把加减速控制方法所涉及的十几种加速度变化模式简化为3种加速度变化模式，避免了复杂、繁琐的计算，降低了理解难度。

(2)提出的算法利用牛顿迭代理论对S形加减速控制方法所涉及的五元非线性方程组进行求解，并根据加减速时间的实际意义，对迭代值进行迭代修正，使得计算结果的切实可行。

(3)本论文算法在求解时，所需要的计算时间更短，精度更高，求出的时间能很好地满足加工要求，减少了机床运动的冲击和振荡，特别适合高速高精加工，提高了机床的加工精度和效率。

[1]黄艳,李家霁,于东,等.CNC系统S型曲线加减速算法的设计与实现[J].制造技术与机床,2005(3):55-58.

Huang Yan,Li Jiaqi,Yu Dong,et al.Design and Implementation of S_shape Acceleration and Deceleration Algorithm on CNC System[J].Manufacturing Technology and Machine Tool,2005(3):55-58.

[2]罗钧,汪俊,刘学明,等.基于S型加减速的自适应前瞻NURBS曲线插补算法[J].计算机集成制造系统,2013,19(1):55-59.

Luo Jun,Wang Jun,Liu Xueming,et al.Adaptive NURBS Interpolation Algorithm with Look-ahead Function Based on S-shape Acceleration Deceleration[J].Computer Integrated Manufacturing Systems，2013，19(1)：55-59.

[3]Ren Kun,Fu Jianzhong,Chen Zichen.Motion Velocity Smooth Link in High Speed Machining[J].Chinese Journal of Mechanical Engineering,2007,20(2):17-20.

[4]乔志峰. 适用于复杂形面加工的多轴运动控制系统设计理论与方法研究[D].天津:天津大学,2012.

[5]潘海鸿,杨微,陈琳,等.全程S曲线加减速控制的自适应分段NURBS曲线插补算法[J].中国机械工程,2010,21(2):190-195.Pan Haihong,Yang Wei,Chen Lin,et al.Adaptive Piecewise NURBS Curve Interpolator Algorithm for Entireness Process S-curve ACC/DEC Control[J].China Mechanical Engineering,2010,21(2)：190-195.[6]南京工程学院.运动控制系统S曲线加减速的实现方法：中国，201310683011.X[P].2014-04-09.

[7]穆海华,周云飞,严思杰,等.超精密点对点运动三阶轨迹规划精度控制[J].机械工程学报,2008,44(1):126-127.

Mu Haihua,Zou Yunfei,Yan Sijie,et al.Precision Control of Third-order Profile Planning for High Accuracy Point-to-point Motion System[J].Journal of Mechanical Engineering,2008,44(1):126-127.

[8]郭新贵,李从心.一种新型柔性加减速算法[J].上海交通大学学报,2003,37(2):205-207.

Guo Xingui,Li Congxin.A New Flexible Acceleration and Deceleration Algorithm[J].Journal of Shanghai Jiaotong University,2003,37(2):205-207.

[9]徐瑞民.二元非线性方程组求根的牛顿迭代[J].山东轻工业学院学报,2009,23(4):90-91.

Xu Ruimin.Newton’s Method for the Nonlinear Function of Two Independent Variables[J].Journal of Shan Dong Institute of Light Industry,2009,23(4):90-91.

[10]孙玉娥，林浒，李建伟.面向高速加工的样条曲线实时插补算法[J].机械工程学报,2011,47(3):186-191.

Sun Yue,Lin Hu,Li Jianwei.Spline Real-time Interpolation Algorithm for High-speed Machining[J].Journal of Mechanical Engineering,2011,47(3)：186-191.[11]罗福源,游有鹏,尹涓.NURBS曲线S型加减速双向寻优插补算法研究[J].机械工程学报,2012，48(5):147-155.

Luo Fuyuan,You Youpeng，Yin Juan.Research on the Algorithm of NURBS Curve Bidirectional Optimization Interpolation with S-type Acceleration and Deceleration Control[J].Journal of Mechanical Engineering,2012,48(5):147-155.

(编辑张洋)

Research on Algorithm of S_shape Acceleration and Deceleration Time Based on Newton Iterative Method

Yang Liangliang1,2Xu Shoujin1,2Shi Weimin1,2Ge Hongwei1,2

1.Zhejiang Provincial Key Lab of Modern Textile Machinery & Technology,Hangzhou,310018 2.Zhejiang Sci-Tech University,Hangzhou,310018

Due to S_shape acceleration and deceleration control involved solving multiple high-order equation or inequality,and the final solution was non negative,so that it was difficult to calculate.Therefore nonlinear equations of five independent variables of S_shape acceleration and deceleration control were decomposed into two nonlinear equations of two independent variables and a linear equation according to time optimal principle and the constraints of speed,acceleration.The final solutions were obtained by Newton iterative method and the iterative correction method then the velocity curve and interpolation algorithm were found.The simulation and experiments were presented to prove that the algorithm is simplicity,stable operation and the ability to meet the requirements of high speed and high precision of computer numerical control.

S_shape acceleration and deceleration control;nonlinear equations of five independent variables;Newton iterative method;time optimal principle

2014-09-19

国家自然科学基金资助项目(51305404)；国家科技支撑计划资助项目(2013BAF05B01)

TP391< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.07.010

杨亮亮,男,1978年生。浙江理工大学机械与自动控制学院讲师、博士。主要研究方向为高速高精运动控制、数控技术、发表论文20余篇。许守金，男，1989年生。浙江理工大学机械与自动控制学院硕士研究生。史伟民,男,1965年生。浙江理工大学机械与自动控制学院教授、博士。葛宏伟,男,1990年生。浙江理工大学机械与自动控制学院硕士研究生。