并联机构承载能力分析

苑飞虎　赵铁石,2　赵延治,2　翁大成

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

并联机构承载能力分析

苑飞虎1赵铁石1,2赵延治1,2翁大成1

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

采用显式求解法计算最大外载荷的极大值，提出了一种基于拉格朗日函数的比例法来计算最大外载荷的极小值。为引入构件重力和惯性力的影响，提出等效驱动力的概念，在此基础上将并联机构用于运动模拟台时的承载能力分为静态承载能力和动态承载能力，并基于比例法给出承载能力的计算过程。最后以六自由度并联机构为例，分析了位姿对承载能力和承载性能指标的影响。研究结果为重载并联机构的优化设计和性能评价提供了参考。

承载性能；承载能力；比例法；等效驱动力；运动模拟台

0　引言

相比于串联机构，承载能力强是并联机构经常被提及的突出优点。对于重载并联机构，承载能力分析和评价更为重要。文献[1-6]将机构“广义力椭球”的长径和短径看作机构在该位姿处能承受广义力的极大值和极小值，并以该极值作为评价机构的承载能力的指标，该方法对多个主动力之间的关系进行了限制，与实际情况不吻合，因此，承载能力评价结果不直观。文献[7-8]分别采用比例法和显式求解法研究平面3RRR机构所能承受的最大力极值。Garg等[9]将上述两种方法应用于空间3RRRS机构的研究。比例法通过多次改变给定方向寻找最大力(力矩)的极值，计算量巨大；显式求解法计算快捷，但不能得到最大力的极小值。此外，有学者根据并联机构的具体应用来研究其承载能力。文献[10-14]以沿固定轨迹运动时机构所能承载的最大负载质量作为机构的承载能力。

本文对并联机构的承载性能和承载能力进行了研究。定义了并联机构承载性能指标，以指导或评价机构的构型设计，并给出了该极值计算方法。基于等效驱动力的概念，研究了并联机构用于运动模拟台时的静态承载能力和动态承载能力。

1　承载能力与承载性能指标的定义

宏观上，承载能力指空间上的最大容量或力学上的最大限度。按照上述理解，并联机构的承载能力可定义为并联机构中输出构件所能承受的最大外载荷，根据用途的不同，此外载荷可以是力，也可以是在一定条件下与力有对应关系的其他物理量，如质量、加速度等。

由文献[15]可得并联机构力平衡方程：

FG+FI+FE=Gff

(1)

式中，Gf为力映射矩阵；FG、FI分别为机构构件重力、惯性力；FE为外载荷；f为驱动力。

由式(1)可知，f取得极值时对应的FE反映了并联机构的承载能力，FE与机构构型、构件结构、驱动器性能和机构运动状态有关，并不能直观地反映机构构型设计的优劣。

机构在某一确定位姿下，FG、FI与构件的具体结构和机构的运动状态有关，而Gf固定不变。Gf由机构构型和结构参数确定，能够反映并联机构的本质。因此，可以基于Gf研究机构的承载性能，以指导和评价机构构型设计。

不考虑机构构件重力和惯性力，将式(1)中FE记为F，有

F=Gff

(2)

此时f取得极值，F的取值完全由机构构型和结构参数确定，其值可以反映机构构型设计的优劣，为机构选型和参数优化设计提供指导。

为具有通用性，驱动力中每个元素极值均设定为单位1，将此时机构在某位姿下所有方向上所能承受最大外载荷的极值定义为并联机构的局部承载性能指标(localcarryingperformanceindex,LCPI)。外载荷中力和力矩具有不同量纲，故应分开处理。令

(3)

其中，‖maxFf‖、‖minFf‖分别为驱动力f取得极值时F的力极大值和力极小值。用ILCP(Fmax)、ILCP(Fmin)评价某一位姿下并联机构的力承载性能，其值越大，则机构的力承载性能越好。当ILCP(Fmax)=ILCP(Fmin)时，机构在该位姿处力各向同性。令

(4)

其中，‖maxFτ‖、‖minFτ‖分别为驱动力f取得极值时F的力矩极大值和力矩极小值。用ILCP(τmax)、ILCP(τmin)评价某一位姿下并联机构的力矩承载性能，其值越大，则机构的力矩承载性能越好。当ILCP(τmax)=ILCP(τmin)时，机构在该位姿处力矩各向同性。

LCPI仅能反映某确定位姿时机构承载性能的好坏，而机构往往在一个特定的工作空间内运行，需要在一个工作空间范围内去评价机构的承载性能。为此，将LCPI在整个可达工作空间内的平均值定义为并联机构的全局承载性能指标(globalcarryingperformanceindex,GCPI)。令

(5)

其中，W表示机构的整个工作空间，w表示机构的某一位姿。用IGCP(Fmax)、IGCP(Fmin)评价整个工作空间范围内机构的力承载性能，其值越大，则机构的力承载性能越好。令

(6)

用IGCP(τmax)、IGCP(τmin)评价整个工作空间范围内机构的力矩承载性能，其值越大，则机构的力矩承载性能越好。

并联机构的承载性能完全由机构构型和结构参数确定，而这两方面正是并联机构设计的基础，LCPI和GCPI可以为并联机构，尤其是重载并联机构的构型选取和参数设计提供指导。

2　外载荷极值计算

研究并联机构的承载性能，即求取驱动力中每个元素极值均为1时最大外载荷的极大值和极小值。本节采用显式求解法求最大外载荷的极大值，采用基于拉格朗日函数的比例法求最大外载荷的极小值。

2.1显式求解法求极大值

将式(2)中F表示为力和力矩的组合形式：

(7)

其中，Ff表示力，Fτ表示力矩。

记Ff、Fτ的维数分别为k和d，则由式(7)得

(8)

其中，fr×1为f中任意r个元素组成的r×1列向量，fs×1为构成fr×1后f中剩余的s个元素组成的列向量。hτ1、hf1由hτ、hf中与fr×1对应的元素组成，hτ2、hf2由hτ、hf中与fs×1对应的元素组成。Od×k为d×k型零矩阵，Ek×k为k×k型单位矩阵，Ok×1为k×1零向量。

记s+r=n，即f为n维列向量。若机构的外力为纯力，即Fτ=0，可认为机构不能转动，只有k个移动自由度。任选d个主动关节并任意给定其驱动力的值，则其余k个驱动力与外力有唯一确定的对应关系。当最大外力取得极大值时，上述任选的d个主动关节的驱动力取得极值。

(9)

其中，hτ1、hf1、hτ2、hf2均可根据f1×s确定。

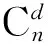
若外载荷为纯力矩，由式(7)得

(10)

同理可得驱动力极值为1时机构所能承受最大外力矩的极大值，该外力矩即maxFτ。

2.2基于拉格朗日函数的比例法求极小值

由式(7)得

(11)

若动平台上外载荷为纯力，由式(11)得

f=gfFf

(12)

对于f中第i个元素if，有

if=ia1x1+ia2x2+…+iakxk

(13)

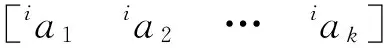
当FfTFf=1时，有

(14)

为求FfTFf=1时if的最大值，构造拉格朗日函数：

(15)

分别对x1,x2,…,xk和λ求偏导，并令其等于0，得

(16)

解得

q∈{1,2,…,k}

将xq代入式(13)，可得if的极值，由于xq可有两个不同取值，故可得2k个if的值。令

ib=max(|if(1)|,|if(2)|,…,|if(2k)|)

(17)

则ib为FfTFf=1时if的最大允许取值，根据xq可确定此时外力载荷的方向，记为iFfq。令

maxb=max(1b,2b,…,nb)

(18)

maxb为FfTFf=1时驱动力所有元素的最大允许取值。若maxb=rb，其中，r∈{1,2,…,n}，则当驱动力极值为1时，机构在该位姿处所能承受的最大外力载荷的极小值minb=1/rb，方向为rFfq，minbrFfq即minFf。

同理可求得机构所能承受的最大外力矩载荷的极小值，该外力矩即minFτ。

3　承载能力分析

并联机构应用场合不同时，其外载荷类型也不相同。本节以运动模拟台为应用背景，研究机构的承载能力。用于运动模拟台时，并联机构的工作方式可分为两种:一种是实现负载的期望位姿，而对运动参数无要求。若机构从当前位姿运动到期望位姿的运动时间足够长，可认为该过程中机构的速度、加速度均为零，这种工作方式称为静态工作；另一种是带动负载实现期望的运动规律，这种工作方式称为动态工作。根据上述两种工作方式，将用于运动模拟台时并联机构的承载能力分为静态承载能力和动态承载能力。

3.1等效驱动力

在设计重载并联机构时，机构构件的重力和惯性力不能忽略。由式(1)可知，并联机构可承受的外载荷由驱动力决定。将式(1)表示为

(19)

驱动力f表示为fI与fE之和，其中，fI对应构件重力和惯性力，fE对应外载荷。当动平台运动规律确定后，构件重力和惯性力FG+FI也是确定的，即fI是确定的，此时fE的取值范围决定了FE的极限值。

fI中元素ifI的值可根据式(19)确定。由f=fI+fE可知，fE中元素ifE的取值极限为

(20)

为保证并联机构能够运动，须满足

-ifm≤ifI≤ifm

(21)

(22)

由式(20)和式(22)可以看出，ifE允许取值范围的跨度与驱动器输出力范围跨度相同，但极限值超过了驱动器的输出极限值。fE是驱动器与机构构件共同作用下可用于平衡外载荷的驱动力，此处将fE称为等效驱动力。

3.2静态承载能力

并联机构静态工作时，外载荷只有负载的重力。机构应能够带动负载达到工作空间内的任意位姿，因此，将整个工作空间范围内动平台均能承受的负载重力的最大值称为机构的静态承载能力。负载重力与质量有确定的对应关系，所以静态承载能力也可以用负载质量描述。

任意位姿w下负载的重力均保持不变，记重力的方向为eg，将Ff=eg代入式(12)，得

feg=gfeg

(23)

其中，feg表示该位姿下平衡重力方向的单位力所需的等效驱动力。

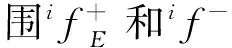
(24)

其中，ifeg为feg中第i个元素。

取ibeg的最小值

(25)

按上述方法可求得整个工作空间范围内每个位姿下机构可承受的最大负载重力。求其最小值：

(26)

则并联机构的静载承载能力为fg，其等价表述为机构可承载的负载最大质量为fg/g，g为重力加速度。

3.3动态承载能力

并联机构带动负载运动时，负载对其作用力包括重力和惯性力。负载确定后，重力保持不变，惯性力主要由负载的加速度确定。因此，可用负载确定时机构所能实现的最大加速度来衡量并联机构的动态承载能力。由并联机构动力学模型可知，加速度与机构的位姿、速度有关，另外用于运动模拟台时机构是按照给定方向运动的，因此，评价并联机构的动态承载能力时应指明其位姿、速度、负载和动态承载能力的方向。

记负载质量为m，惯性矩阵为J。在某位姿w下，动平台速度为V。并联机构分支构件t速度Vt与动平台速度的映射为

(27)

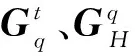
由动平台速度产生的分支构件t的加速度vAt与动平台速度的映射为

(28)

则由动平台速度产生的分支构件t的惯性力为

(29)

其中mt、Jt分别为构件t的质量和惯量，vAta、vAt ε分别为vAt中线加速度分量和角加速度分量，Vt ω为Vt中角速度分量。

动平台及负载由速度产生的惯性力为

(30)

其中，O为元素均为0的列向量，Vω为V的角速度分量，J0为动平台和负载的惯量。

根据文献[16]，由动平台速度产生所有构件和负载的惯性力等效到动平台为

(31)

其中，GFt为构件t到动平台的力传递矩阵，T表示机构分支构件的个数。

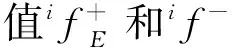
记所求最大加速度方向为e，则该方向上负载单位加速度对应的分支构件t的加速度为

(32)

由动平台单位加速度产生的分支构件t的惯性力为

(33)

其中，aAta、aAt ε分别为aAt的线加速度分量和角加速度分量。

动平台及负载由单位加速度产生的惯性力为

(34)

其中，m0为动平台和负载的质量和。

由动平台加速度产生的所有构件和负载的惯性力等效到动平台为

(35)

将FE=aFI代入式(19)，可得给定方向上产生单位加速度所需的等效驱动力：

(36)

令

(37)

其中，ife为fe中第i个元素。

取ice的最小值

ce=min(1ce,2ce,…,nce)

(38)

则cefe中至少有一个元素取得极限值。由于fe与e成线性关系，故动平台此时可产生的e方向最大加速度为ce，即在位姿w下，动平台速度为V时，并联机构在e方向上的动态承载能力为ce。

4　数值算例

对于某六自由度并联机构，某位姿下其力映射矩阵为

Gf=

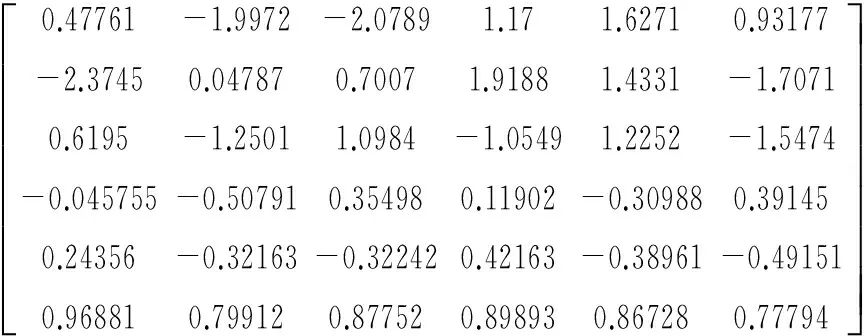
采用本文方法和文献[7]方法分别求该位姿下机构所能承受的最大外力矩载荷极值及其方向，见表1。

表1　最大外力矩载荷极值及方向

可以看出，两种方法结果基本相同，从而验证了本文方法的正确性。文献[7]方法在搜索次数达3×106时结果稳定，而本文方法求极大值、极小值分别需要搜索120次、48次即可，显然本文方法效率更高。对于最大外力载荷极值的计算有相同结论，不再赘述。

针对某重型战车的运动模拟需求，首先对备选构型Stewart机构、6-PUS机构的承载性能进行比较。

结构参数相同时，Stewart平台与6-PUS机构工作空间相似，在此条件下比较两机构的承载性能。给定动平台铰链点外接圆半径为2.5m，动平台铰链点夹角θa=17°，基础平台铰链点外接圆半径为2.86 m，基础平台铰链点夹角θb=13°，动平台初始高度H=4.41 m，移动副长度变化范围为-1.5～1.5 m。根据式(5)、式(6)求Stewart机构和6PUS机构的全局承载性能指标IGCP，见表2。

表2　Stewart机构和6-PUS机构的全局承载性能指标

由表2可以看出，两种机构的全局承载性能指标相差不大，6-PUS机构承载性能更好。基于6-PUS机构的并联运动模拟台及相关坐标系如图1所示。

图1　基于6-PUS机构的并联运动模拟台

将动平台绕x轴、y轴、z轴角位移分别记为rx、ry、rz，沿这三个轴的位移记为tx、ty、tz。改变其中一个角位移或位移而保持其他5个量不变，可得动平台沿该方向转动或移动时LCPI的变化规律，如图2～图7所示。

图2　LCPI随rx变化曲线

图3　LCPI随ry变化曲线

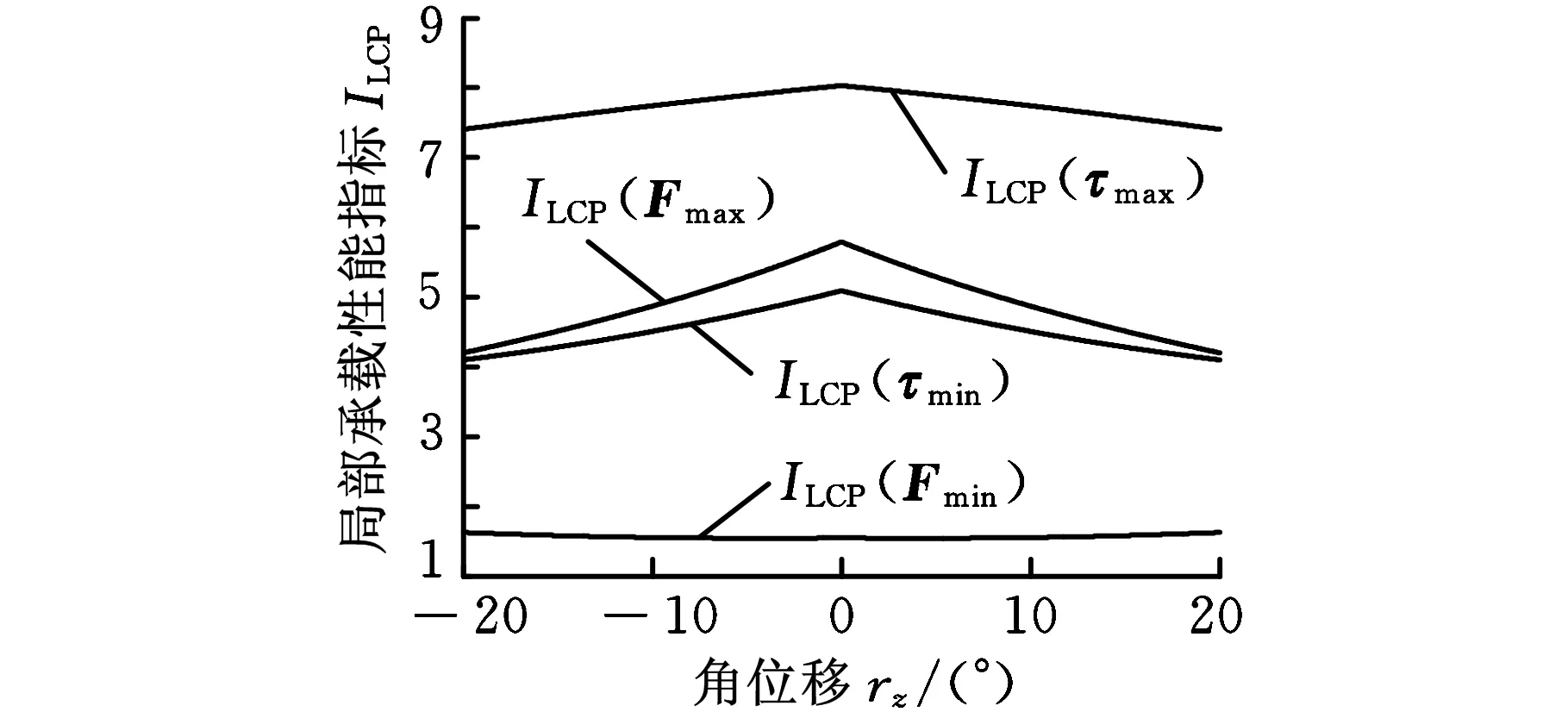
图4　LCPI随rz变化曲线

图5　LCPI随tx变化曲线

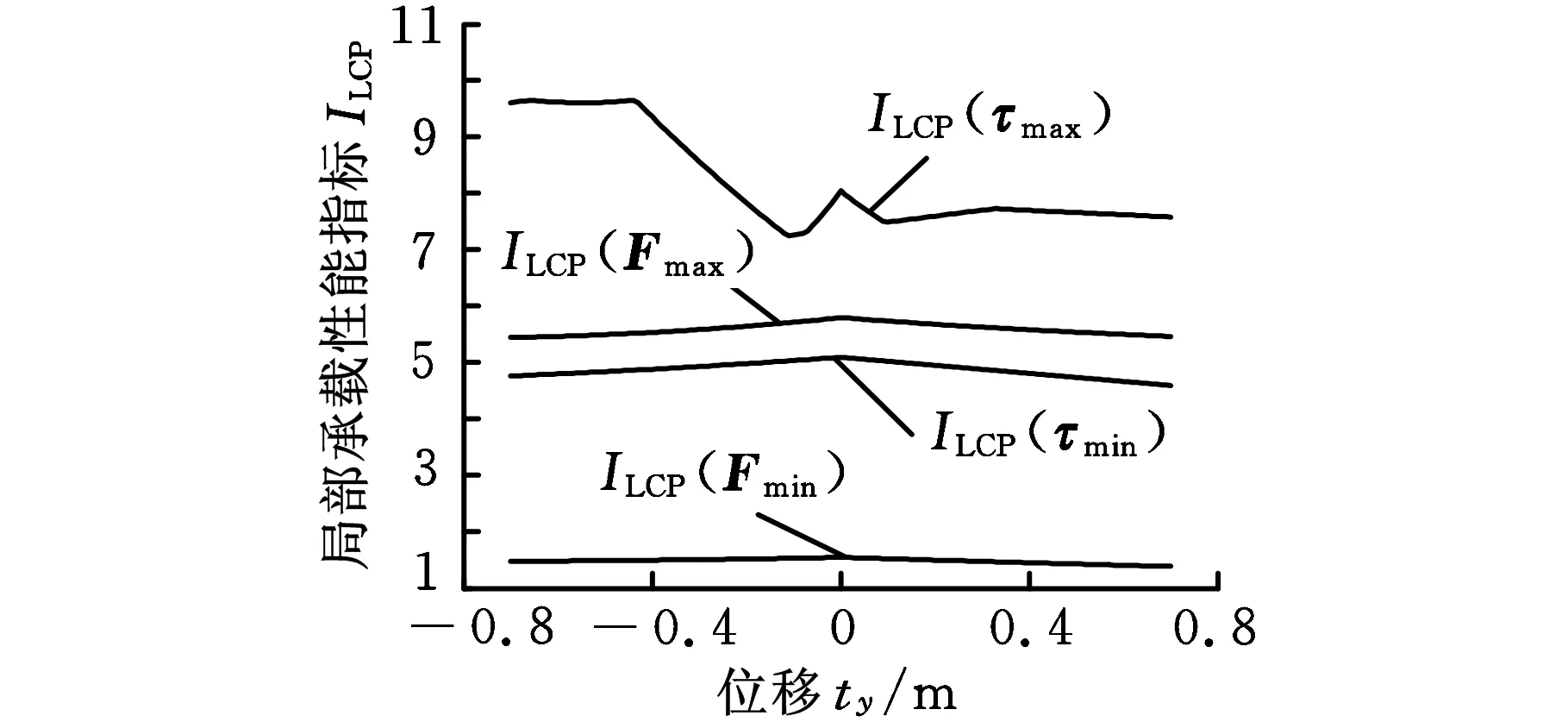
图6　LCPI随ty变化曲线

图7　LCPI随tz变化曲线

由图2～图7可以看出，机构位姿对ILCP(τmax)影响最大，而对ILCP(Fmin) 、ILCP(τmin)、ILCP(Fmax)影响较小。在初始位姿处机构的局部承载性能最好。

基于6-PUS机构的并联运动模拟台支撑杆质量为545kg，滑块质量为332kg，动平台质量为12.3t。电机额定扭矩为290N·m，丝杠导程为0.04m，减速器减速比为1∶4。根据式(26)，并联机构的静态承载能力为57.2t。

负载质量为36t，与动平台固连后其整体对x轴、y轴、z轴转动惯量均为16 386kg·m2。在初始位姿，动平台速度为零时，机构沿(绕)x轴、y轴、z轴的动态承载能力见表3。

表3　基于6-PUS机构的并联运动模拟台动态承载能力

由表3可以看出，该模拟台动态承载能力强，可以用于大、重型设备的运动模拟。6-PUS机构竖直方向的移动动态承载能力大于其水平方向的移动承载能力，绕y轴的转动动态承载能力大于其他两个方向的转动承载能力，而初始位姿处y轴正是该机构的一条对称轴线。

5　结论

(1)本文忽略机构构件重力和惯性力，将驱动力极值为1时并联机构所能承受的最大外载荷的极值定义为并联机构承载性能指标，以反映机构构型设计的优劣，为并联机构，尤其是重载并联机构构型选取和参数设计提供了指导。

(2)计算并联机构承载性能指标时采用基于拉格朗日函数的比例法，所得结果准确，计算效率高。

(3)结构参数相同时，6-PUS机构承载性能优于Stewart机构。6-PUS机构适用于大、重型设备的运动模拟。该机构在初始位姿处局部承载性能最优。用于运动模拟台时，对于移动，竖直方向的动态承载能力大于水平方向；对于转动，绕机构对称轴线的动态承载能力大于其他方向。

[1]Pasquale C,Yann B V,Fransois P.Evaluation of Force Capabilities for Redundant Manipulators[C]//International Conference on Robotics and Automation.Piscataway,1996:3520-3525.

[2]刘辛军.并联机器人机构尺寸与性能关系分析及其设计理论研究[D].秦皇岛：燕山大学，1999.

[3]张立杰,刘颖,黄真.平面2自由度驱动冗余并联机器人的性能分析[J].机械工程学报, 2006, 42(7): 181-185.

Zhang Lijie,Liu Ying,Huang Zhen.Analysis of Performances of Planar 2-dof Parallel Manipulator with Actuation Redundancy[J].Chinese Journal of Mechanism Engineering,2006,42(7): 181-185.

[4]张立杰.平面两自由度驱动冗余并联机器人的承载能力分析[J].机械设计与研究, 2003,19(1): 28-30.

Zhang Lijie.Analysis of Carrying Capacity of Planar 2-dof Parallel Manipulator with Actuation Redundancy[J]. Journal of Machine Design and Research,2003,19(1): 28-30.

[5]金振林, 陈贵林, 高峰. 新型三维平台机床全域承载能力及其在几何空间模型内的分布[J].机械设计,2002,6(6): 25-27.

Jin Zhenlin,Chen Guilin,Gao Feng.Analysis of Global Carrying Capacity of a New Type Three-dimensional Platform Machine and Its Distribution in Geometric Spatial Model[J].Journal of Machine Design,2002,6(6): 25-27.

[6]韩江义，游有鹏，王化明，等.并联机构力传递的分析[J].机器人，2009，31(6)：523-528．

Han Jiangyi,You Youpeng,Wang Huaming,et al.Analysis on Force Transmission of Parallel Mechanism[J].Robot, 2009, 31(6): 523-528．

[7]Nokleby S B,Fisher R,Podhorodeski R P,et al.Force Capabilities of Redundantly-actuated Parallel Manipulators[J].Mechanism and Machine Theory,2005,40(5):578-599.

[8]Zibil A,Firmani F,Nokleby S B,et al.An Explicit Method for Determining the Force-moment Capabilities of Redundantly Actuated Planar Parallel Manipulators[J].Journal of Mechanical Design,2007,129:1046-1055.

[9]Garg V,Nokleby S B,Carretero J A.Wrench Capability Analysis of Redundantly Actuated Spatial Parallel Manipulators[J].Mechanism and Machine Theory,2009,44:1070-1081.

[10]Chen Chunta,Zeng Shichang.Optimal Configuration of a Parallel Kinematic Manipulator for the Maximum Dynamic Load-carrying Capacity[C]//First International Conference on Robot:Vision and Signal Processing.Piscataway,2011:122-125.

[11]Korayem M H,Bamdad M.Dynamic Load-carrying Capacity of Cable-suspended Parallel Manipulators[J].The International Journal of Advanced Manufacturing Technology,2009,44(7/8): 829-840.

[12]Korayem M H,Bamdad M,Tourajizadeh A,et al.Analytical Design of Optimal Trajectory with Dynamic Load-carrying Capacity for Cable-suspended Manipulator[J].The International Journal of Advanced Manufacturing Technology,2012,60:317-327.

[13]Korayem M H,Ghariblu H.The Effect of Base Replacement on the Dynamic Load Carrying Capacity of Robotic Manipulators[J].The International Journal of Advanced Manufacturing Technology,2004,23(1):28-38.

[14]Korayem M H,Bamdad M,Sharareh B.Optimal Trajectory Planning with Maximum Load Carrying Capacity for Cable Suspended Robots[C]//6th International Symposium on Mechatronics and Its Applications.Piscataway,2009:1-6.

[15]黄真，赵永生，赵铁石.高等空间机构学[M].北京：高等教育出版社，2003.

[16]陈修龙，冯伟明，赵永生.五自由度并联机器人机构动力学模型[J].农业机械学报,2013,44(1): 236-243.

Chen Xiulong,Feng Weiming,Zhao Yongsheng.Dynamics Model of 5-DOF Parallel Robot Mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2013,44(1): 236-243.

(编辑陈勇)

Analysis of Load Carrying Capacity of Parallel Mechanism

Yuan Feihu1Zhao Tieshi1,2Zhao Yanzhi1,2Weng Dacheng1

1.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System,Yanshan University, Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science,Ministry of Education of China,Yanshan University,Qinhuangdao,Hebei,066004

The explicit method was used to calculate the maximum extreme of the maximum external load. To get the minimum extreme of the maximum external load, a scaling foctor method was presented based on Lagrange function. Taking into account the effects of components’ gravities and inertial forces,the concept of equivalent driving force was presented.Based on this concept,the static carrying capacity and dynamic carrying capacity of parallel mechanism used as motion simulation platform was discussed. The calculation process was put forward based on scaling foctor method.Using a six DOF mechanism as an example,the effects of mechasim poses on carrying capacity and carrying performance indexes was analyzed.A reference to guide and evaluate the design and performance of heavy load parallel mechanism is put forward.

load carrying performance;load carrying capacity;scaling foctor method;equivalent driving force;motion simulation platform

2014-05-04

国家自然科学基金资助项目(51375420，50975244，51105322)

TP24< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.07.004

苑飞虎，男，1986年生。燕山大学机械工程学院博士研究生。主要研究方向为并联机器人理论与应用。赵铁石，男，1963年生。燕山大学机械工程学院教授、博士研究生导师。赵延治，男，1981年生。燕山大学机械工程学院副教授。翁大成，男，1990年生。燕山大学机械工程学院硕士研究生。