强非共沸工质R134a/R23/R14汽液相平衡和压焓图的构建及应用

张庆庆，张华，娄江峰，李佳，赵巍，王袭，刘占杰



强非共沸工质R134a/R23/R14汽液相平衡和压焓图的构建及应用

张庆庆1，张华1，娄江峰1，李佳1，赵巍1，王袭2，刘占杰2

（1上海理工大学制冷与低温工程研究所, 上海 200093；2海尔集团技术研发中心，山东青岛 266101）

基于PR状态方程，分模块模拟计算了三级自动复叠制冷系统中R134a/R23/R14三元混合工质的热物理特性参数，得到非共沸混合工质的汽液平衡数据、两相组分，并利用干度计算焓熵值，构建了典型配比下混合工质的压焓图和汽液相平衡图。二元R134a/R23和R32/R134a混合工质的泡点压力和气相组分的计算值与实验测试值的误差分别小于1.3%、1.2%和1.0%、2.4%；三元R32/R125/R134a混合工质95%的计算值与实验值的偏差在±5%之内，表明该模型能满足工程计算需要。利用理论模型，结合实验系统，对R134a/R23/R14三级自动复叠制冷系统进行详细的组分等热物性分析，并在空间压焓图上进行了详细表述。

自动复叠制冷；混合物；PR状态方程；热力学性质；计算机模拟；压焓图

引 言

多级自动复叠制冷系统已广泛应用于低温制冷领域，国内外学者的相关研究[1-4]主要集中在系统循环的优化设计和混合制冷工质的配比优选两个方面。虽然在实验基础上的系统优化设计取得了显著成果，如采用带喷嘴的两级自动复叠机组可在低压缩比下稳定运行且具有较高的性能系数[5]；采用三级自动复叠机组可在176 K的低温下获得0.253的COP[6]。但对循环过程中混合制冷剂物性的研究非常有限，目前研究人员主要通过实验经验优选混合制冷剂的配比，极少会对系统中混合制冷剂组分进行进一步的研究，因此系统运行过程中混合制冷剂物性的数据非常缺乏，不利于自动复叠系统的优化。

在研究团队大量关于自动复叠制冷系统实验的基础上[7-10]，通过采用PR状态方程，模拟计算了用于自动复叠制冷系统中R134a/R23/R14三元非共沸混合工质的热物理特性参数，重点模拟二元、三元非共沸混合工质在一定配比下的汽液平衡数据。主要包括：泡露点的计算；给定温度压力下混合工质状态的判断，并计算相应的干度、气液相组分和焓熵；最后通过该模型对实验运行时的混合工质组分进行计算分析，评估系统装置运行状态，构建了R134a/R23/R14经典配比下的系统压焓图，详细描述了系统循环。提出的二元、三元混合工质的热物性计算模型可为自动复叠制冷系统提供大量可靠的数据，同时为混合工质的物性模拟研究提供参考。

1 混合工质物性计算模型

1.1 混合工质状态方程

混合工质的物性模拟计算选用PR[11]状态方程。PR方程既适用于气相也适用于液相，其计算气相密度的精度与PKS状态方程相当，但计算液相密度的精度高于PKS方程[12]；该方程比Helmoholtzh能量混合法方程[13]简单，只含有两个参数和，只需知道工质的临界参数及偏心因子，便能计算工质所有的热力性质。PR方程具体表达式为

方程的压缩因子形式如下

3-(1-)2+(-32-2)-(-2-3)=0 (2)

1.2 混合规则

对于混合工质，使用PR方程时常采用van der Waals covolume混合规则计算两个混合参数m和m，形式如下

(4)

式中，x、x为混合工质各组分的摩尔分数；k为二元交互作用系数，常见工质的k可查阅相关资料[14-15]获得；但用在三级自动复叠系统中的中低温工质二元交互作用系数k数据非常缺乏，可以通过k关联模型[16-17]计算获得。

1.3 汽液相平衡时泡露点求解模块

汽液相平衡时，气液相温度、压力相等，各相组分的逸度相等v=f，用逸度系数和组分摩尔比表示为vy=x。混合工质中组元的逸度系数可由式(5)计算得出。

(6)

式中，v和f是组分在气相和液相中的逸度；v和是组分在气相和液相中的逸度系数；y和x是组分在气相和液相中的摩尔分数，K是组分的相平衡常数。汽液相平衡一般有4种情况：① 已知温度初始配比，求对应泡点压力和气相组分；② 已知温度初始配比，求对应露点压力和液相组分；③ 已知压力初始配比，求对应泡点温度和气相组分；④ 已知压力初始配比，求对应露点温度和液相组分。图1是已知压力和初始配比，求解对应露点温度和液相组分的计算流程图，其他3种情况的求解流程图类似。

1.4 两相区在汽液平衡时组分x和y的求解模块

混合工质以一定摩尔比z混合后，给定温度压力下，可以通过对比泡露点压力或温度，判断混合工质此时的状态，如果处在两相区，需要对混合工质的干度和气液相组分进行求解，设干度为，干度的求解目标函数为

使用斜截法求解目标函数，需要对目标函数求导

(8)

其中

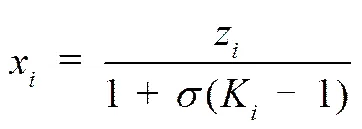
图2是基于以上理论对两相区干度和气液相组分求解的流程。

1.5 混合工质的焓、熵的求解模块

在上述模块求解得到混合工质各相组分和干度的前提下，采用余函数法计算混合工质的焓和熵[18]。

余焓和余熵在PR方程中的表达式为

r=r+r+M(1-) (10)

(11)

采用IIR(International Institute of Refrigeration)标准确定焓熵的基准点，工质在温度为273.15 K时的饱和液体的比熵与比焓分别为1.0 kJ·kg-1·K-1和200 kJ·kg-1。上角标“*”表示在相同温度、压力下，把流体看成理想气体时相应的各项热力性质，具体流程如下。

由温度压力和气相摩尔比y，解PR方程，3个根中的最大实根是气相压缩因子（气相比容），代入式(9)～式(11)计算气相混合物的理想熵*v和理想焓*v，余熵vr和余焓vr；由温度压力和液相摩尔比x，解PR方程，3个根中的最小实根是液相压缩因子（液相比容），代入式(9)～式(11)计算液相混合物的理想熵*l和理想焓*l，余熵sr和余焓hr。图3是对混合工质给定温度压力下所处状态（过冷、两相区或者过热）判断并对其焓熵求解的流程。

2 模拟结果与分析

该模型适用于任意二元或多元工质在任意配比时的物性模拟，主要对用于自动复叠制冷系统常见的二元、三元混合制冷剂进行了热物性的模拟，并将模拟结果与实验数据和美国标准局（NIST）制定的REFPROP软件数据进行了对比分析。

图4是R134a/R23模拟结果与实验数据[19]的误差，从图中可看出压力模拟数据与实验值的误差小于2.0%，平均误差为1.3%；气相组分的模拟数据与实验值的平均误差为1.2%。此外，图4还比较了实验数据和NIST计算数据之间的误差，发现平均误差为0.5%，且比NIST软件结果更接近实验值。由于应用在复叠系统中的非共沸混合工质的沸点相差很大，关于这些混合工质的汽液平衡数据鲜有报道，为了充分验证该模型的准确性，进一步比较了R32/R134a的模拟结果，图5显示了R32/R134a的模拟结果与文献[20]中实验值的误差。由图中可知，压力模拟数据与实验值的误差小于2.0%，平均误差为1.0%；气相组分的模拟数据与实验值的平均误差为2.4%，模拟结果同样优于NIST软件计算值。

图5(b) 是R32/R134a气相组分的模拟数据与实验结果比较，主要呈现出较大的负偏差，即混合工质中R32的气相组分模拟计算值小于实验测量值，原因之一，参考文献实验时测量的误差；原因之二，PR状态方程在预测液体容积时稍高，这一缺陷在R32/R134a上表现明显，但在可接受范围内。为论证推广到三元混合工质物性参数的计算准确度，进一步比较了R32/R125/R134a三元混合工质的模拟结果，图6是其计算值与实验值[21]的对比，95%的计算值与实验值的偏差在±5%之内，90%的计算值与实验值的偏差在±3%之内，满足工程应用需求。

图7是初始质量比为60/40的R23/R14混合工质，通过模块模拟计算得到的压焓图，准确度与NIST软件进行了比较。模拟计算了54个点（22个过热气体点，14个过冷液体点，18个两相区点），模拟焓值与NIST的平均误差为0.88%，熵值平均误差为0.77%，符合实际应用的精度要求。

由图4、图5看出，一定程度上，该模型模拟结果优于NIST模拟的结果，并且还具有NIST REFPROP软件不具有的优点。NIST REFPROP没有公布具体的模拟模型和模拟参数，该模型的模块都可以在最新汽液平衡实验的基础上，改进混合工质的相互影响因子等参数优化模型，从而提高模拟的准确度，具有很高的开放性和优化性；对于REFPROP软件无法计算、高压区域PR方程计算误差较大的参数点，该模型采用在其附近区域参数“插值”的方法来计算其状态参数。由于该模型采用模块模拟，每个模块间可以很方便地灵活调用，软件内部各模块的相互调用比调用外部软件具有更快的计算速度，如图8所示是R134a/R23/R14 = 0.16/0.36/0.48混合工质分别使用REFPROP软件和使用该模型计算得到的压焓图，使用该模型可以避免在调用REFPROP时因图8所示问题出现求解不出的情况。

图8 局部压焓图计算结果比较(R134a/R23/R14)Fig. 8 Comparison of pressure-enthalpy diagrams for R134a/R23/R14(R134a/R23/R14=65/20/15)

3 系统性能分析

在研究团队对三级自动复叠制冷系统的实验基础上[22]，使用该模型对系统性能进行分析。系统选用R134a/R23/R14混合工质作为制冷剂，质量比为经典配比65/20/15，系统稳定运行时高压2.3 MPa，低压0.22 MPa。图9是单级压缩三级自动复叠制冷循环示意图。图10是模拟得到的系统运行压力下，各级混合工质配比与对应泡露点温度情况的相平衡态，可用于制冷工质初始组分选配分析[9]。

A— compressor; B—condenser; C—dry filter; D—high-temperature phase separator; E—high-temperature valve; F—recuperator; G—high-temperature evaporative condenser; H—middle-temperature phase separator; I—middle-temperature valve; J—recuperator; K—low-temperature evaporative condenser; L—low-temperature valve; M—evaporator; N—expander; P,Q—join points; 1～19—temperature measurement points

R134a/R23/R14三级自动复叠制冷系统采用混合工质，混合工质的组分在运行过程中有分离和混合的过程[23]，混合工质组分的改变主要发生在气液分离器和分凝换热器中。通过该模型计算得到气液分离器D中气相组分比R134a/R23/R14=46/27/27，液相组分比R134a/R23/R14=84/13/03。气相混合物通过冷凝换热器，温度逐渐降低提纯低温工质的含量，冷凝换热器制冷剂侧进出口温差为3-5=35℃，在其内发生的是复杂的传热传质过程。为简化计算，提出宏观上的分段冷凝模型。从制冷剂入口到出口分成段空间，假设每一段内的温度、压力、组分不变，各段的温度逐段降低。第段温度，压力不变等于高压侧压力，混合工质在这一段空间内冷凝。如果较大则每段可以看成处在汽液平衡状态。已知、、z，通过两相区在汽液平衡时组分x和y的求解模块计算得到气液相组分，气相组分进入下一段进一步冷凝，则下一段的初始组分等于这一段计算得到的气相组分z+1=y。由第一段初始组分为3点计算得到的气相组分1=46/27/27，在上述模型基础上取=7迭代计算出5点组分比R134a/R23/R14=14/35/51。分凝换热器可以进一步提纯低温组分，为了提高循环的可计算性可忽略通过高温级气液分离器底部的混合液体中的R14成分，即通过高温级节流阀的液体是R134a/R23的混合物。4点和17点组分相同、节流前后焓相同，假设R134a/R23混合工质组分初值，由实验测得的温度压力利用混合工质焓熵模块计算得到4、17，判断4=17?若不相等调整混合工质组分，继续循环计算；若相等则跳出循环。最后循环得到4、17点的混合工质比R134a/R23=80/20，再已知混合工质组分、温度、压力就可以判断4、17点的状态，4点的泡点温度为317.5 K，过冷度为14.37 K。同理得到7点的组分R134a/R23/R14= 25/47/28，8点组分R23/R14=22/78，7点的泡点温度为237.74 K，过冷度为2.59 K。4点的过冷度很大，而7点的过冷度不大。分析原因，在分凝换热器F中，混合工质入口第一段初始组分是根据3点得到1=46/27/27，在此配比下，=2.3 MPa时，dew=306.77 K>5=272.15 K，在F中发生冷凝，较冷冷凝液体由F回到气液分离器D中，所以4点过冷度很大；而在分凝换热器J中，混合工质入口第一段初始组分是根据6点得到1=0/22/78，在此配比下，=2.3 MPa时，dew=228.05 K<8=228.15 K，所以在J中温度始终高于露点温度，没有发生冷凝，没有较冷液体回到气液分离器H中，所以7点的过冷度较小。

表1是在实验数据基础上，通过模拟计算得到的自动复叠系统中各点的状态参数。由表1可以清楚地看到系统运行稳定时各个部件中的气液组分情况，也得到了热力分析需要的各点热力参数，包括干度、气液相组分和焓熵等。在传统的工程应用中，为了简化热力计算经常假设高低温组分在气液分离器中完全分离，即混合工质通过高温级气液分离器D后4点的组分为R134a，5点的组分为R23/R14；在通过中温级气液分离器H后7点的组分为R23，8点的组分为R14。通过表1，可以看到混合工质通过高温级气液分离器D后4点组分为R134a/R23的混合物，R23的组分占到了20%，而不是传统假设的R134a纯工质流。5点的组分中仍含有R134a，比例为14%。在通过中温级气液分离器H后8点的组分为R23/R14的混合物，R23的比例为22%，而不是传统假设的R14纯工质流。可见对循环过程进行准确的热力分析必须对混合工质热物性进行计算，进而才能对系统性能进行较准确的评估。

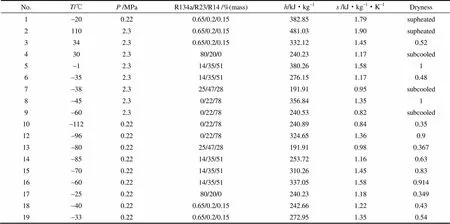
表1 循环过程中各点热力计算Table 1 Calculated thermodynamic properties of auto-cascade system

制冷循环过程习惯用压焓图表示，但在三级自动复叠制冷系统中无法用一个压焓图直观地表示，该系统涉及到二元与三元不同比例混合工质的压焓图，所以想要准确用压焓图表示R134a/R23/R14三级自动复叠制冷循环过程必须计算一定比例下的R134a/R23、R23/R14和R134a/R23/R14的热力学物性。在表1计算得到组分比的基础上，通过该模型计算得到了质量比为R134a/R23=80/20，R23/R14= 22/78，R134a/R23/R14=65/20/15，R134a/R23/R14 = 25/47/28，R134a/R23/R14 = 14/35/51的压焓图，进一步得到图11，由图11可以详细看到系统中各点状态及系统循环过程。

4 结 论

通过对R134a/R23/R14三级自动复叠制冷系统的理论和实验研究分析，得到如下结论。

（1）基于PR方程，通过斜截法，分模块准确模拟了用在该复叠系统中的R134a/R23/R14三元工质的热物性，包括汽液平衡泡露点的求解，并提出以干度为目标函数进行气液相组分的求解，并进一步利用干度对混合工质气液相焓熵求解，给出了详细的物理模型和流程图。

（2）通过R134a/R23和R32/R134a的模拟结果与汽液平衡实验数据进行对比，发现汽液平衡压力模拟结果平均误差小于1.3%和1.0%；组分的模拟结果平均误差分别小于1.2%和2.4%，比NIST计算结果更接近实验值；也给出了R23/R14质量比0.6:0.4时的压焓图，与NIST平均误差小于1.0%，模拟结果满足工程应用的需要。

（3）在实验数据的基础上，应用该模拟程序对系统进行了组分分析，具体给出了各混合工质在运行压力下的汽液平衡图；对设备各点进行了热力计算，得到系统运行稳定时各个部件中的气液组分情况，给出了系统循环过程的空间压焓图，并与传统分析进行比较，发现必须对混合工质热物性进行计算才能准确评价系统性能。

References

[1] Kim S G, Kim M S. Experiment and simulation on the performance of an autocascade refrigeration system using carbon dioxide as a refrigerant [J]., 2002, 25(8): 1093-1101.

[2] Gong Maoqiong, Wu Jianfeng, Cheng Quiwei, Sun Zhaohu, Liu Jiayong, Hu Qinguo. Development of a-186℃ cryogenic preservation chamber based on a dual mixed-gases Joule-Thomson refrigeration cycle [J]., 2012, 36(1): 188-192.

[3] Wang Q, Li S H, Wang J P, Sun T F, Han X H, Chen G M. Numerical investigation on the performance of a single-stage auto-cascade refrigerator operating with two vapor-liquid separators and environmentally benign binary refrigerants [J]., 2013, 112: 945-955.

[4] Du Kai, Zhang Shaoqian, Xu Weirong, Niu Xiaofeng. A study on the cycle characteristics of an auto-cascade refrigeration system [J]., 2009, 33(2): 240-245.

[5] Yu Jianlin, Zhao Hua, Li Yanzhong. Application of an ejector in autocascade refrigeration cycle for the performance improvement [J]., 2008, 31(2): 279-286.

[6] Sivaakumar M, Somasundaram P. Exergy and energy analysis of three stage auto refrigerating cascade system using zeotropic mixture for sustainable development [J]., 2014, 84: 589-596.

[7] Rui Shengjun(芮胜军), Zhang Hua(张华), Huang Lihao(黄理浩). Pressure characteristics of auto-cascade refrigeration system [J].(化工学报), 2012, 63(S2): 176-180.

[8] Rui Shengjun(芮胜军), Zhang Hua(张华), Zhang Qinggang(张庆钢), Huang Lihao(黄理浩). Characteristics of two-stage segregation auto-cascade refrigeration system [J].(化工学报)，2013, 64(6): 2019-2035.

[9] Zhao Wei(赵巍), Zhang Hua(张华), Liu Ruixi(刘瑞希), Xiao Chuanjing(肖传晶), Zhang Shuchun(张书春). Study on mixed refrigerants selecting and matching of a four stage auto-cascade refrigeration [J].(制冷学报), 2013, 34(5):17-22.

[10] Rui Shengjun(芮胜军), Zhang Hua(张华), Huang Lihao(黄理浩), Yu Zida(喻子达), Wang Xi(王袭), Wang Xiaoying(王晓影). Theory and experimental study of two-stage auto-cascade low temperature refrigerator [J].(机械工程学报), 2014, 50(2): 159-164.

[11] Peng D Y, Robinsion D B. A new two-constant equation of state [J]., 1976, 15(1): 59-64.

[12] Li H, Yan J. Evaluating cubic equations of state for calculation of vapor-liquid equilibrium of CO2and CO2-mixtures for CO2capture and storage processes [J]., 2008, 86(6): 826-836.

[13] Lemmon E W, Jacobsen R T. A generalized model for the thermodynamic properties of mixture [J].1999, 20(3): 825-835.

[14] Agelia M Abudour, Sayeed A Mohammad, Robert L Robinson Jr, Khaled A M Gasem. Generalized binary interaction parameters for the Peng-Robinson equation of state [J]., 2014, 383:156-173.

[15] Liu Yanni(刘燕妮), Guo Kaihua(郭开华), Lu Laiyun(鹿来运). Vapor-liquid equilibrium measurements for tetrafluoromethane + propane system [J].(化工学报), 2013, 64(10): 3514-3519.

[16] Fang Jin(方锦), Hou Shuxin(侯树鑫), Duan Yuanyuan(段远源), Song Yixin(宋艺新). Evaluating of vapor-liquid equilibrium models for refrigeration mixture containing hydroflurocarbons [J].:(清华大学学报：自然科学版), 2008, 48(11): 1940-1944.

[17] Hu Peng(胡芃), Gao Jingxuan(高静轩), Chen Longxiang(陈龙祥), Chen Zeshao(陈则韶). Prediction of vapor-liquid equilibria for binary and ternary HFC/HC mixtures using PR equation of state and vdW mixing rule [J].(化工学报), 2012, 63(2): 350-355.

[18] Scalabrin G, Grigiante M, Cristofoli G. Modelling enthalpy and entropy of pure and mixed refrigerants with an innovative corresponding states method [J]., 2003, 26(8): 936-950.

[19] Lim J S, Park K H, Lee B G, Kim J D. Phase equilibria of CFC alternative refrigerant mixtures: binary systems of HFC23+HFC134a and HFC23+HEC227ea at 283.15 and 293.15K. [J]., 2001, 46(6):1580-1583.

[20] Cui Xiaolong, Chen Guangming, Li Changsheng, Han Xiaohong. Vapor-liquid equilibrium of difluoromethane+1,1,1,2-tetrafluoroethane systems over a temperature range from 258.15 to 343.15 K [J]., 2006, 249(1/2):97-103.

[21] Nagel M, Bier K. Vapor-liquid equilibrium of ternary mixtures of the refrigerants R32, R125 and R134a [J]., 1995, 18(8):534-543.

[22] Lu Xiangyang(陆向阳). The experimental study of three-stage auto-cascade refrigeration system [D]. Shanghai: University of Shanghai for Science and Technology, 2004.

[23] Gong M Q, Wu J F, Luo E C, Qi Y F, Hu Q G, Zhou Y. Research on the change of mixture compositions in mixed-refrigerant Joule-Thomson cryocoolers [J]., 2002, 47(B): 881-887.

Construction and application for VLE and pressure-enthalpy diagrams of R134a/R23/R14 zeotropic mixtures

ZHANG Qingqing1,ZHANG Hua1,LOU Jiangfeng1,LI Jia1,ZHAO Wei1,WANG Xi2,LIU Zhanjie2

(1Institute of Refrigeration and Cryogenic Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China;2Haier Group Technology R & D Center, Qingdao 266101, Shandong, China)

The thermodynamic properties of R134a/R23/R14 ternary mixtures used in three-stage auto-cascade refrigeration systems were calculated based on the PR equation, and enthalpy and entropy were calculated by using dryness. The diagrams of pressure-enthalpy and VLE of R134a/R23/R14 mixture under the typical composition were given. The deviations of bubble pressure and vapor composition between simulation results and the experimental data were less than 1.3% and 1.2% for R134a/R23, 1.0% and 2.4% for R32/R134a, respectively. The deviations of 95% calculated values of R32/R125/R134a were between ±5%. The simulation results could meet the requirements of engineering calculation. Based on the experiment, the thermodynamic properties of the auto-cascade refrigeration system were analyzed in detail. The pressure-enthalpy diagrams of R134a/R23, R23/R14 and R134a/R23/R14 under the operating compositions were given, and the diagram of spatial pressure-enthalpy described the circle of this system clearly. This simulation program could analyze the system circle effectively.

auto-cascade refrigeration; mixtures; PR equation; thermodynamic properties; computer simulation; pressure-enthalpy diagram

10.11949/j.issn.0438-1157.20141676

TB 657.3

国家自然科学基金项目(51176124)；国际科技合作项目(2012DFR70430)。

2014-11-12.

Prof. ZHANG Hua, Zhanghua3000@163.com

supported by the National Natural Science Foundation of China (51176124) and the International S&T Cooperation Program of China (ISTCP) (2012DFR70430).

A

0438—1157（2015）07—2387—08

2014-11-12收到初稿，2015-04-23收到修改稿。

联系人：张华。第一作者：张庆庆（1988—），女，硕士研究生。