考虑温度约束的单杂质水网络优化

李瑞臻，冯霄，王彧斐



考虑温度约束的单杂质水网络优化

李瑞臻，冯霄，王彧斐

（中国石油大学(北京)重质油国家重点实验室，北京 102249）

实际用水过程有温度的要求，在用水网络集成中考虑温度的约束，使水耗和能耗同时降低，具有重要的意义。此外，过程系统中还存在只有温度限制的与用水无关的过程流股，将水网络中的水流股与其同时考虑热集成，可以使能量得到更合理的分配利用。在全过程系统能量集成的背景下，建立了对应的水网络优化方法。首先使用现有的废水直接回用水网络LP模型求解初始水网络并提取流股数据，然后在4条非等温混合规则的判断下，依次比较水网络流股与背景夹点、全过程夹点的关系，以排除不合理的非等温混合，最后以年总费用最低为目标进行全过程系统的热集成。使用本文提出的方法对某案例进行优化，得到的年总费用减少了6.27%，证明了该方法的可行性。

水网络；优化；热集成；全过程系统

引 言

水是人类赖以生存的重要资源，随着世界人口数目的增长，水资源愈发短缺，其价格也日益高涨。化工生产过程作为用水大户，正面临着越来越大的经济和环境压力，节水减排势在必行。

水系统集成能够显著提高水的重复利用率。其通常分为两大类方法：概念法和数学规划法。概念法发展得较早，在Wang等[1]提出水夹点法基础上，陆续出现水源水阱复合曲线[2]、水剩余曲线图法[3]、水级联法[4]和物料回收夹点图法[5]等方法。虽然这些方法简单易行，但是在设计大规模系统时更多需要依赖设计者经验，所得结果不一定最优。

由于概念法存在以上缺陷，数学规划法逐渐成为研究的热点。Takama等[6]首先建立了水网络超结构和相应的非线性规划数学模型，之后Savelski等[7]对单杂质用水网络的最优化条件进行了分析和证明，并将最小连接数纳入目标函数以获得较简洁的水网络结构[8]。另外，Teles等[9]建立了废水直接回用水网络的超结构模型，以及初始化策略和求解策略，可以更容易地得到最优解。

在实际的化工生产过程中，用水过程有温度的要求，需要将水加热或者冷却来满足该要求。此外，过程中还存在大量的只有温度限制的与用水无关的过程流股，可以用来加热或冷却水流。所以如果能够在提高水资源利用率的基础上同时考虑能量的回收利用，使水耗和能耗同时降低，将具有重要的现实意义。

考虑能量集成的水网络设计方法主要有两种路线：一种路线是基于夹点原理的概念设计法；另一种路线是基于超结构的数学规划法。概念设计法首先由Savulescu等[10-11]进行了系统性的研究，他们依次引入了分离系统和双维格子图等图形方法来分步求解用水和用能目标。Leewongtanawit等[12]在此基础上添加了新的流股混合规则，降低了原网络的复杂度，进一步降低了换热器的数目。概念设计法具有物理意义明确、易执行等优点，但是难以应用于大规模系统，并且在解决费用或成本等类型的目标值时有其局限性。数学规划法通过建立合理的数学模型，在确定某一目标函数的情况下获得水网络和换热网络的结构。Bagajewicz等[13]通过状态空间法表达网络结构，得到了基于用水网络最优性必要条件和换热网络转运模型的网络数学模型。随后，廖祖维等[14]探索了区分直接传热和间接传热的研究工作，并将其推广到操作可分解的情况[15]。

在考虑温度约束的水网络中，非等温混合是一种非常有效的换热方式，不仅换热的流股不需要有温差，而且在换热过程中也不需要换热器。但是由于非等温混合可能会造成公用工程用量增加，所以以往的研究大多都建立在等温换热的基础上，对非等温换热的研究近年来才开始进行。毛庭璧等[16]通过建立非等温换热的问题表格得到了非等温混合规则，运用此规则判断非等温混合是否产生能量惩罚。Liao等[17]将流股分割并将非等温混合和等温混合分开计算。

由于水网络内的能量回收有限，而全过程系统内的能量集成可以使能量的利用更加合理有效，所以本文将以全过程系统热集成为背景进行水网络求解。首先建立水网络模型，以新鲜水用量最少为目标，求解优化后的水网络结构。之后在背景夹点的基础上提出4个非等温混合规则，应用于水网络中以减少部分不合理非等温混合。接下来将水网络中的流股与其他过程流股进行热集成，以包含冷热公用工程费用、设备固定费用和换热面积费用的总年费用最少为目标，求解热网络结构。根据水网络和热网络的优化结果，最终得出考虑温度约束的水网络结构。

1 水网络模型的建立及求解

1.1 问题描述

给定一系列用水单元，每个用水单元对操作温度和水质都有要求，提供用水单元的温度、极限进出口浓度和需移除的污染物负荷。给定新鲜水源的污染物浓度和温度，以及最后排放废水污染物的排放浓度和温度要求。优化目标为新鲜水用量最少。为了建立较为简洁的水网络数学模型，本文做出下列假设：

（1）水系统中的过程单元均为连续操作过程，且操作过程恒温；

（2）水的比热容与杂质浓度与水的温度无关，水的比热容为4.2 kJ·kg-1·K-1，流股间总传热系数为定值；

（3）间接换热的最小温差为10℃；

（4）只有一种新鲜水源，杂质浓度为0，初始水温为20℃，废水排放温度要求达到30℃；

（5）忽略操作单元及流股的热量和质量损失生成；

（6）用水单元出口废水不再回用至原用水单元。

1.2 水网络超结构模型

常规的废水直接回用水网络超结构模型[18]如图1所示，对于用水过程，新鲜水流股FW在混合器M与来自任一用水单元的流股F,j混合为其来水，排水经过分割器S，可以直接作为废水WW排放或被其他用水单元回用（F,i）。该数学模型的约束方程[19]可表述如下：

图1 废水直接回用水网络超结构模型

混合器M的流量平衡约束为

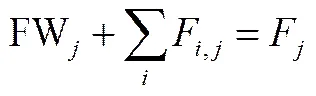
式中，FW为进入用水单元的新鲜水流量，kg·s-1；F,j为用水单元到的水流量，kg·s-1；F为进入用水单元的水流量，kg·s-1。

用水单元的流量平衡约束为

式中，F,i为用水单元到的水流量，kg·s-1；WW为用水单元排放的废水流量，kg·s-1。

结合浓度单调性准则和最大允许浓度准则[7]，用水单元杂质负荷质量平衡约束为

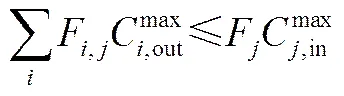
(4)

式中，L为用水单元需除去的杂质负荷，g·s-1；、、分别为用水单元的进出口极限浓度、用水单元的极限出口浓度，mg·L-1。

由于所有变量均不能为负值，故非负约束为

FW，F,j，F,i，F，WW≥0 (5)

由式(1)～式(4)可知，该水网络模型约束均为线性约束。

以最小新鲜水量为目标函数

对于该模型，本文使用数学规划及优化软件GAMS进行求解。

2 非等温混合规则的提出

在水网络中，往往会出现一些流股混合的情况，而且这些流股的初始温度也不一定相等，所以可能会出现非等温混合的情况。根据文献[16]的研究，非等温混合可能会增加公用工程用量。因此本节将提出一些非等温混合规则，以避免可能不合理的非等温混合情况。在全过程系统热集成的前提下，本文首先定义水网络以外的换热流股的夹点为背景过程夹点，水网络流股和其他过程流股汇总后得到的夹点为全过程夹点，并以前节求得的水网络为初始水网络。之后，将初始水网络中的流股依次与背景夹点、全过程夹点进行比较，根据以下4条规则判断初始水网络中的非等温混合是否合理。

（1）夹点以上的热流股和冷流股可以直接混合，这种混合虽然不会减少公用工程量，但是可以减少换热器数量；

（2）夹点以下的热流股和冷流股可以直接混合，这种混合虽然不会减少公用工程量，但是可以减少换热器数量；

（3）夹点以下的热流股尽量与夹点以上的冷流股直接混合，这种混合可能会减少公用工程量，同时可以减少换热器数量；

（4）夹点以上的热流股尽量不与夹点以下的冷流股直接混合，这种混合一定会增加公用工程量。

若初始水网络中存在违背该规则的混合情况，则将不可发生该混合作为额外约束条件，重新求解新的初始水网络结构。重复此过程，直到得出符合规则的初始水网络。

3 全过程系统能量集成的水网络优化步骤

在全过程能量集成背景下的水网络优化步骤如图2所示。首先通过两个循环过程求解水网络的最优结构，之后以综合公用工程费用、换热面积费用和设备固定费的年总费用最低为目标，采用工程类软件Aspen Energy Analyzer V7.3求解全过程系统的换热网络，最终得到具有温度约束的水网络结构。

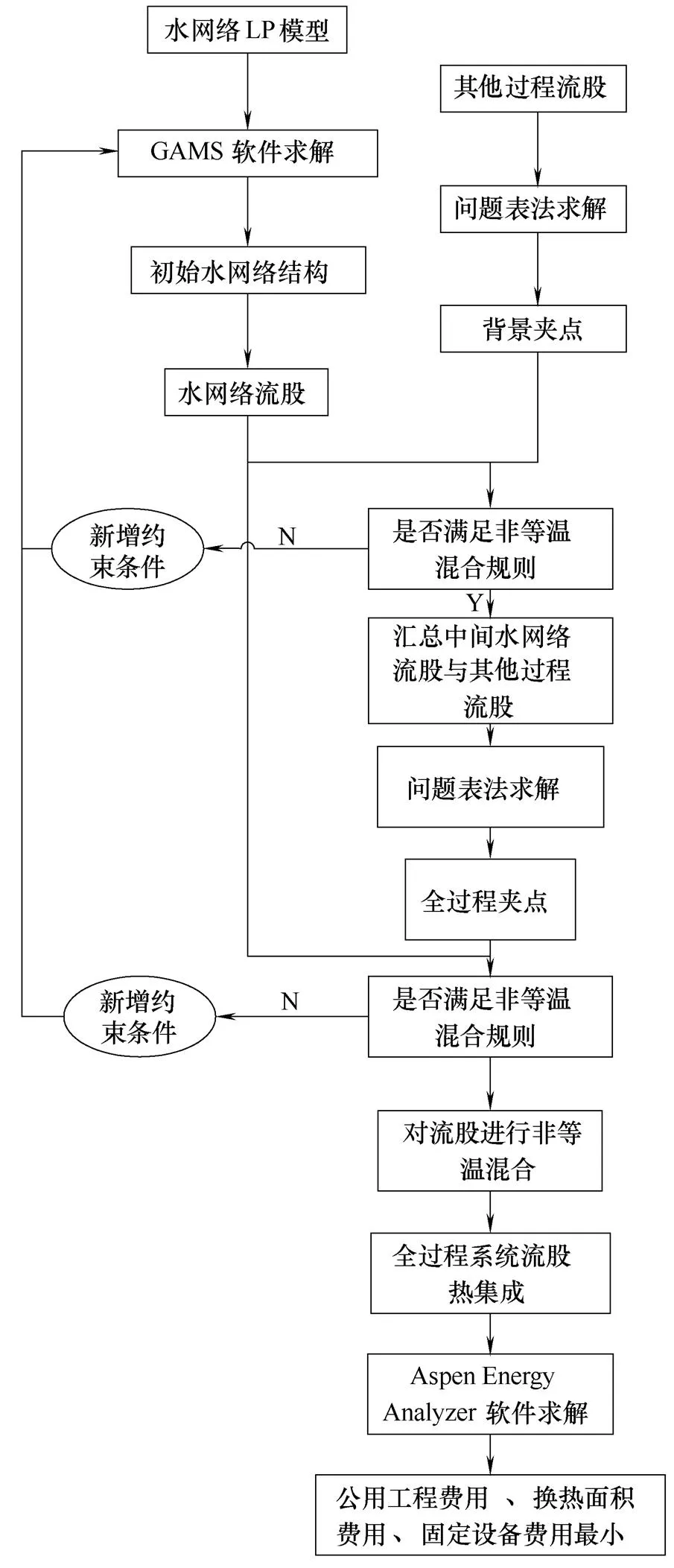
图2 全过程系统能量集成的水网络优化框图

4 案例分析

本文取文献[20]中石油炼制工业的实例来说明以上方法和步骤。该文献中为多杂质体系，这里为了简便，从原始数据中的3种杂质中选取1种关键杂质进行说明。经过计算，发现当系统中只包含杂质盐时，最小新鲜水用量与多杂质时相同，故选取杂质盐为关键杂质。水网络之中和水网络以外的流股原始数据分别见表1和表2。

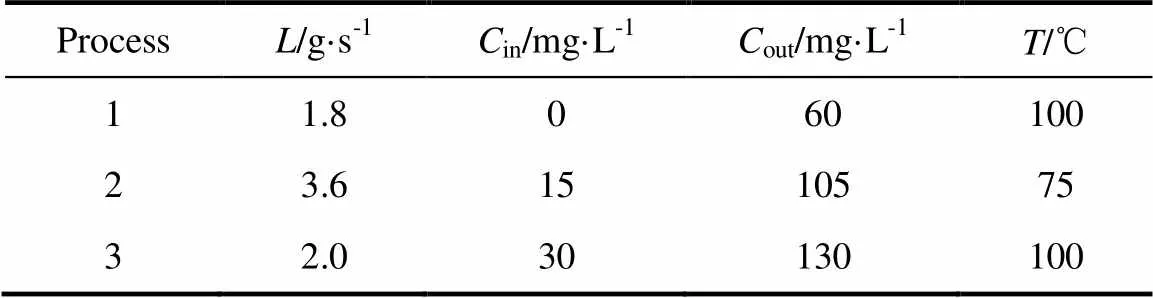
表1 案例的用水单元数据

Note: CCU18.119 USD·kW-1, CHU37.706 USD·kW-1, CFW0.375 USD·t-1,0.8517.

表2 水网络以外的冷热流股数据

根据表2，可以得出除水网络以外的换热流股的热夹点为314/304℃。由于水网络中所有的操作单元温度均在该夹点之下，根据非等温混合规则，水网络中所有的热流股和冷流股均在夹点之下，任意流股均可以直接混合。以新鲜水为最小目标求得的初始水网络见图3，初始水网络的新鲜水量为70kg·s-1。从初始水网络中提取的冷热流股数据见表3。

表3 水网络中的冷热流股数据

图3 案例的水网络结构

将表2和表3中的流股合并计算夹点，夹点没有发生变化，所以可直接进行全过程流股的热集成。根据非等温混合规则，发现Hw1与Cw2可以直接混合，将新流股命名为HC1，混合后的流股属性为40～75℃，热负荷为5880 kW。原文中的年设备固定费和换热面积费用公式取8600+12000.6USD。在Aspen Energy Analyzer V7.3中输入该费用公式，冷热公用工程的价格及总传热系数，以用热年总费用最小为目标求得全过程系统优化后的换热网络见图4，换热器的流股和热负荷数据见表4，最终的具有能量集成的水网络见图5（仅列出水网络中的冷热流股）。图4中，换热网络的年总费用为2612274 USD，由于水网络中新鲜水流量为70 kg·s-1，按照年运行时间8000 h计算，水网络的年费用为756000 USD，故用水和用能的全部年费用为3368274 USD，比原文献中求得的年费用降低了6.27%。

图4 优化的换热网络

表4 换热器流股温度及热负荷数据

图5 考虑能量集成的水网络结构

5 结 论

本文建立了全过程系统能量集成背景下的水网络优化方法，分步求解水网络和换热网络。其中水网络LP模型使用GAMS软件求解，全过程系统的换热网络使用Aspen Energy Analyzer V7.3软件求解。在优化步骤中引入4条非等温混合规则，以排除可能不合理的非等温混合。对案例进行优化后，得到的年费用比文献值降低了6.27%，显示了本文方法的有效性。

符 号 说 明

A——换热器换热面积，m2 C——杂质浓度，mg·L-1 CCU——冷公用工程年单位费用，USD·kW-1 CFW——新鲜水年单位费用，USD·t-1 CHU——热公用工程年单位费用，USD·kW-1 F——流股的质量流率，kg·s-1 FW——新鲜水的质量流率，kg·s-1 L——杂质负荷，g·s-1 M——混合器 P——操作单元 S——分割器 T——用水单元操作温度，℃ U——传热系数，kW·(m2·℃)-1 WW——废水的质量流率，kg·s-1 上角标 max——最大值 下角标 i, j——用水单元 in——进口 out——出口

References

[1] Wang Y P, Smith R. Wastewater minimisation [J]...., 1994, 49 (7): 981-1006.

[2] Dhole V R, Ramchandani N, Tainsh R A, Wasilewski M. Make your process water pay for itself [J]..., 1996, 103 (1): 100-103.

[3] Hallale N. A new graphical targeting method for water minimisation [J]...., 2002, 6 (3): 377-390.

[4] Manan Z A, Tan Y L, Foo D C Y. Targeting the minimum water flow rate using water cascade analysis technique [J].., 2004, 50 (12): 3169-3183.

[5] Prakash R, Shenoy U V. Targeting and design of water networks for fixed flowrate and fixed contaminant load operations [J]...., 2005, 60 (1): 255-268.

[6] Takama N, Kuriyama T, Shiroko K,. Optimal water allocation in a petroleum refinery [J]., 1980, 4 (4): 251-258.

[7] Savelski M J, Bagajewicz M J. On the optimality conditions of water utilization systems in process plants with single contaminants [J]...., 2000, 55 (21): 5035-5048.

[8] Bagajewicz M, Savelski M. On the use of linear models for the design of water utilization systems in process plants with a single contaminant [J]., 2001, 79 (A5): 600-610.

[9] Teles J, Castro P M, Novals A Q. LP-based solution strategies for the optimal design of industrial water networks with multiple contaminants [J]...., 2008, 63 (2): 376-394.

[10] Savulescu L, Kim J K, Smith R. Studies on simultaneous energy and water minimisation (Ⅰ): Systems with no water re-use [J]...., 2005, 60 (12): 3279-3290.

[11] Savulescu L, Kim J K, Smith R. Studies on simultaneous energy and water minimization (Ⅱ): Systems with maximum re-use of water [J]...., 2005, 60 (12): 3291-3308.

[12] Leewongtanawit B, Kim J K. Improving energy recovery for water minimisation [J]., 2009, 34 (7): 880-893.

[13] Bagajewicz M, Rodera H, Savelski M. Energy efficient water utilization systems in process plants [J]...., 2002, 26 (1): 59-79.

[14] Liao Zuwei (廖祖维), Yang Yongrong (阳永荣), Wang Jingdai (王靖岱), Jiang Binbo (蒋斌波). Optimization of energy efficient water utilization systems [J].() (化工学报), 2007, 58 (2): 396-402.

[15] Liao Zuwei, Wu Jintao, Jiang Binbo, Wang Jingdai, Yang Yongrong. Design energy efficient water utilization systems allowing operation split [J]....., 2008, 16 (1): 16-20.

[16] Mao Tingbi (毛庭璧), Luo Yiqing (罗祎青), Yuan Xigang (袁希钢). Design method of heat intergrated water networks considering non-isothermal mixing [J].(化工学报), 2010, 61 (2): 369-377.

[17] Liao Z, Rong G, Wang J, Yang Y. Systematic optimization of heat-integrated water allocation networks [J]....., 2011, 50 (11): 6713-6727.

[18] Huang C H, Chang C T, Ling H C, Chang C C. A mathematical programming model for water usage and treatment network design [J]....., 1999, 38 (7): 2666-2679.

[19] Liu Zuming (刘祖明), Luo Yiqing (罗祎青), Yuan Xigang (袁希钢). Synthesis of heat-integrated water allocation network considering non-isothermal mixing [J].(化工学报), 2014, 65 (1): 285-291.

[20] Du Jian (都健). Study on design of water utilization network involving energy intergration and flexibility [D]. Dalian: Dalian University of Technology, 2004.

Water network optimization with temperature constraints

LI Ruizhen, FENG Xiao, WANG Yufei

(State Key Laboratory of Heavy Oil Processing, China University of Petroleum, Beijing 102249, China)

In a practical water using process, a temperature requirement exists. Thus, it is significant to consider the temperature constraint in water network integration to decrease the water and energy consumption at the same time. Besides, there are non-water process streams which only have temperature requirements in the process system. If these streams are integrated with water streams in the water network, better energy efficiency can be reached. In this paper, a method for optimizing water networks is proposed under the background of heat integration in whole process system. First, an LP model is established to obtain the initial status of the water network and stream data. Then, four rules for non-isothermal mixing are proposed by comparing the relative position of water streams with the background and whole process pinches to exclude the irrational non- isothermal mixing. Finally, the heat integration in the whole system is performed with minimal total annual cost as the objective function. A case study is used to show the feasibility of the method, which can get a decrease of 6.27% in the annual cost.

water network; optimization; heat integration; whole process system

2015-01-29.

supported by the NSFC-ANR Project (21261130583).

Prof. FENG Xiao, xfeng@cup.edu.cn

10.11949/j.issn.0438-1157.20150142

TQ 021.8

A

0438—1157（2015）07—2581—07

NSFC-ANR项目（21261130583）。

2015-01-29收到初稿，2015-04-08收到修改稿。

联系人：冯霄。第一作者：李瑞臻（1986—），男，硕士研究生。