浅析初中数学类比思维的培养

蒋凤兰

摘 要：类比思维是中学数学学习过程中的一种很重要的思维， 它能够将抽象的问题具体化，帮助学生更好地理解数学定理、数学推论、 数学概念等。基于此，本文结合“三以”教学方法，阐述了初中数学类比思维的培养，以期为相关的教育工作提供有益的参考与借鉴，进而提高学生的探究能力、创新素质，从而提高教学效果。

关键词：初中数学；类比思维；培养

类比思维是数学教学上的重要数学思维，能够帮助学生打开思维，活化数学学习，真正为培养学生的创新性精神而服务。在基础教育新课标改革背景之下，初中数学课堂上类比思维的解题方法得到了数学教师们的普遍青睐。基于此，中学教师要重视这种思维能力的训练，才能够逐渐将类比思维过程灌输到学生数学学习习惯中，从而达到培养学生类比思维能力的目的。

一、类比思维与初中数学学习

类比就是由两个对象的某些相同或相似的性质，推断它们在其他性质上也有可能相同或相似的一种推理形式。类比思维在类比中联想，从而升华思维，既有模仿又有创新。类比思维具有联想、启发、假设、模拟等多种功能，在创造性思维中居于重要的地位。类比思维是一种或然性极大的逻辑思维方式，它的创造性，表现在发明创造活动中人们能够通过类比已有事物开启创造未知事物的发明思路，其中隐含有触类旁通的含义。

在初中数学教学与学习中，教师不妨培养学生的类比思维，运用类比思想深入分析和探讨类比方法在课堂教学中的应用。因此，作为基础教育之一的中学数学，在教学中必须重视培养学生的类比推理和归纳推理的能力。学生学习类比思维能把已学习的知识和方法与一些表面看来与之毫不相干的新知识和方法联系起来，寻找创新的目标和解决的方法。这对于提高初中数学质量，帮助学生在高中学习甚至以后的学习中具有深远的意义。笔者认为，在初中数学学习阶段类比思维培养可以从以下三点出发。首先，教师应当根据教材内容编排的特点，在传授新知识时，可以有意识地去引导学生通过类比思维方法得出所要讲授的新知识，以此慢慢让学生掌握类比推理的方法。其次，教师在对学生进行阶段性知识总结复习时，可以借助相关的知识进行类比，以培养学生对相关知识进行类比的习惯。最后，在对学生讲述如何解题教学中，教师通过类比引导学生进行推广数学命题或者从中寻找解题的途径，以达到深化对题目相关考查知识的理解，从而掌握这些数学思想方法。

二、“三以”高效课堂改革

初中数学类比思维的培养中，学习很多知识点时可以通过对比学习，这种对比就是常说的类比思维。下面选取初中数学教学知识点，谈谈“三以”高效课堂改革下如何进行类比思维培养。

1.“以学为主”的类比思维培养

“以学为主”的类比思维是指在课堂上教师要明确本课要教学的内容与学习目标，让学生能够联系以前学习过的相关类似知识点。类比思维是创造性思维的一种形式，有时我们可以从一种研究对象的结论出发，往往能创造出意料之外的喜悦。

例如，在教学人教版七年级《实数》“立方根”内容时，考虑到“平方根”与“立方根”两节在内容与知识展开顺序上是平行的。为此，为建立立方根的概念，可以充分借用平方根的有关概念的产生过程进行类比，新旧知识通过类比联系，既有利于复习巩固平方根知识，又有利于理解和掌握立方根的概念。同样的，要学习一元一次不等式的解法可类比一元一次方程的解法，这样的例子在初中学习中比比皆是。

教师需要把要学习的新知识同已经学习的旧知识紧密联系起来，将知识点进行合理迁移，再通过类比得出另一种研究对象的许多意想不到的结论。正如现代美籍匈牙利数学家波利亚所说：“如果没有相似推理，那么无论是在初等数学还是在高等数学中，甚至在其他任何领域中，本来可以发现的东西，也可能无从发现。”

2.“以思为中心”的类比思维培养

对于初中数学学习，思考是数学学习很重要的一环，是课堂上学生参与互动的基础，学生有了思考才会去解决问题。学生一定要掌握类比思维，类比思维是合情推理中一种重要的思维方式，由简到难，能在数学解题中让题目迎刃而解。例如下面一道例题：

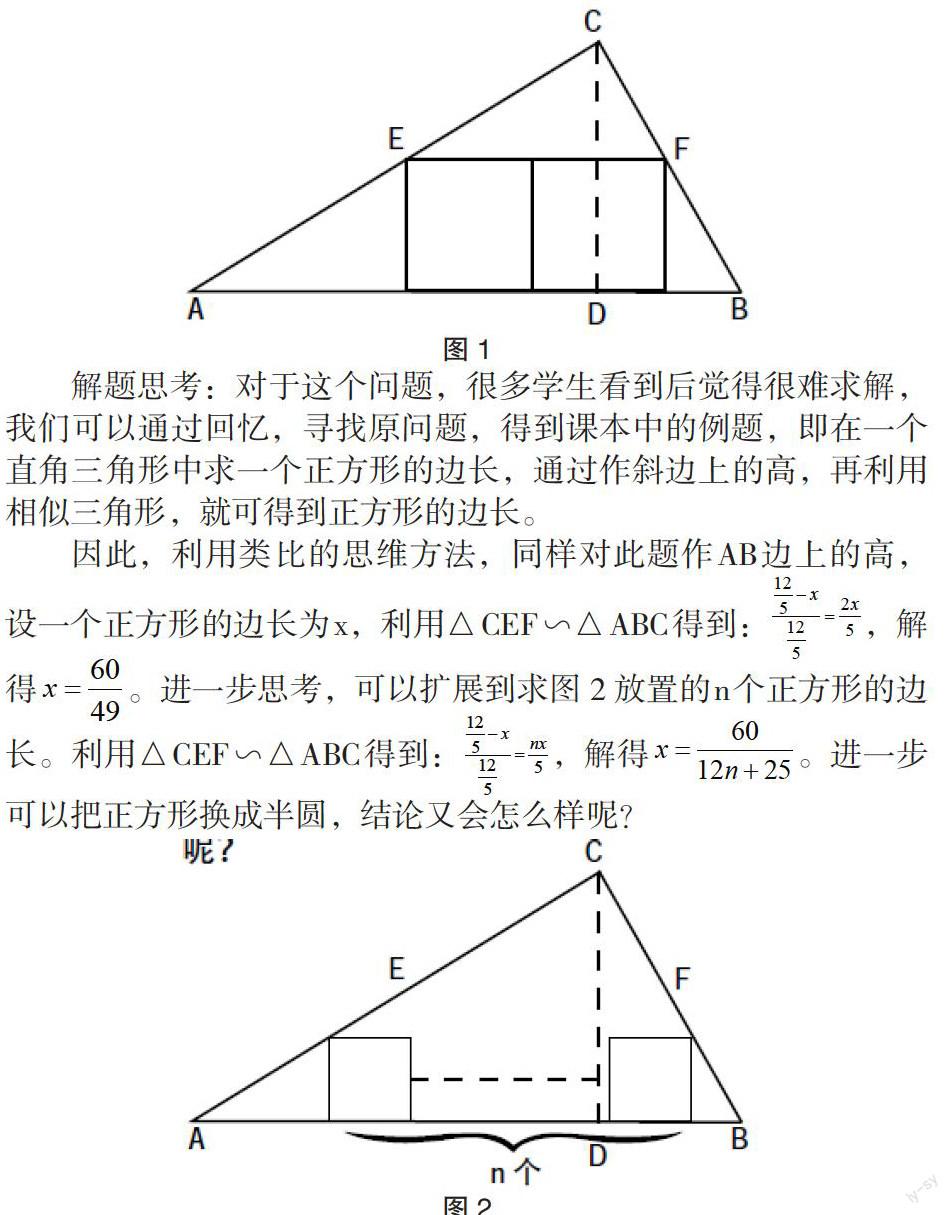
如图1，已知Rt△ABC中，∠C=90°，AC=4，BC=3，求图中放置的两个正方形的边长。

解题思考：对于这个问题，很多学生看到后觉得很难求解，我们可以通过回忆，寻找原问题，得到课本中的例题，即在一个直角三角形中求一个正方形的边长，通过作斜边上的高，再利用相似三角形，就可得到正方形的边长。

因此，利用类比的思维方法，同样对此题作AB边上的高，设一个正方形的边长为x，利用△CEF∽△ABC得到：，解得。进一步思考，可以扩展到求图2放置的n个正方形的边长。利用△CEF∽△ABC得到：，解得。进一步可以把正方形换成半圆，结论又会怎么样呢？

3.“以实践为立足点”的类比思维培养

学习的落脚点在于学生碰到问题能够独立解决，利用类比方法可以深刻地理解概念、公式、定理的实质，分清新旧知识的联系和区别，但是也要防止生搬硬套、发生定式思维的错误。

例如，在人教版七年级上册《线段》中有这么一题：“一条线段上有n个点，问共有几条线段？”解题：每个点出发可以画（n-1）条线段，n个点就构成n（n-1）条线段，但是每2个点之间按照上述方法计算重复了一次，应当要除以2，即n（n-1）条。

运用类比的思想，学生想到八年级《一元二次方程》中一个问题：“一次聚会，出席的每位代表都和其他代表各握一次手，统计结果表明，一共握手45次，问参加聚会的代表有多少人？”解题：设参加聚会的代表有x人。每个人握手的次数是（x-1）次，x人就握了x（x-1）次，但是每2个人之间按照上述方法计算重复了一次，所以要除以2，则有x（x-1）=45。

上述两个问题是看似解题符合道理，其实学生在学习线段的基础上，握手问题易于解决。但在类比思维学习中，不能按其对象表面的相似机械地类比，否则容易得出错误的结论。如果再生搬硬套类比的思维，則就发生思维定式的错误了，在上面聚会握手就不必除以2。为此，在对学生进行类比思维培养时，教师不但要注意问题的共性，又要注意问题的个性。教师对学生在类比过程产生的想法，能确定正误的要及时评价，不能确定的要给予方法的指导，要求学生重新去研究。

三、总论

总之，类比思维方式是初中数学学习中经常运用到的思维方式，在数学学习和解题中起着至关重要的作用。该思维能够帮助学生变迁和发散思路、推广和延伸命题，对于学生数学学习具有举一反三的效果。因此，在教学的过程中，教师们应认真审视、对待它，并且让学生能够掌握并且运用类比思维，进而促进中学生探索发展能力和创新思维能力的培养，实现创新素质教育的要求。

参考文献：

[1]赵莹莹.运用类比思维活化数学教学[J].初中数学教与学.2013（17）.

[2]陈长；孔雯雯.初中数学类比思维解题方法研究[J].吉林教育.2014（25）.