模块化多电平换流器模块冗余优化配置方法

2015-09-19王宝安谭风雷

电力自动化设备 2015年1期

王宝安，谭风雷，商姣

（东南大学电气工程学院，江苏南京 210096）

0 引言

近年来，模块化多电平技术凭借其在多电平领域的巨大优势，深受专家学者们的青睐，对其的研究取得了较大突破，特别在高压变频领域有着广阔的应用前景。在高压变频领域，传统二极管箝位型多电平技术，随着电平数的增加，箝位二极管数量将大幅增加，直流侧电容电压的均衡控制困难，算法复杂，而电容箝位型多电平技术也存在类似的问题；H桥级联型多电平技术[1]，采用模块化控制，使得控制变得相对简单，但是不能提供公共的直流母线，需经过多重移相变压器和整流器产生后给各个模块提供直流电压，这样使得整个装置的成本和体积变大；模块化多电平技术[2-6]，高度模块化，拓展容易，冗余设计简单，无需使用多重化移相变压器，大幅减小了装置体积和重量，降低了成本和损耗。因此，模块化多电平技术越来越受到人们的关注，未来将会成为高压变频领域的主流拓扑结构。

随着电压等级的升高，功率模块数量将大幅提升，长期运行情况下，功率模块故障是不可避免的，为避免其影响系统的正常运行，需要配置冗余模块[7-8]。当工作模块故障时，首先将其旁路，然后用冗余模块代替故障模块工作，保证系统安全、可靠运行。针对冗余子模块数量，配置越多，系统可靠性越高，但成本也越高，且冗余子模块利用率较低，不经济；配置越少，成本较低，但是系统的可靠性得不到保障。因此，合理、有效地配置冗余子模块数量十分重要。但是，目前并没有冗余子模块的定量配置方法。

文献[9]提出了冗余度与可靠性的概念，但是缺乏对冗余子模块配置方法的研究。文献[10]对冗余子模块的配置做出了一定研究，但只是给出了冗余子模块配置的大概范围，没有进一步确定最优冗余子模块配置数量，依然需要工作人员根据实际工程经验进行选择。基于以上分析，本文主要从系统可靠性、冗余子模块有效利用率和冗余子模块数量这3个目标出发，提出一种基于多目标优化的模块化多电平换流器（MMC）模块冗余优化配置方法，并详细给出该方法的实现步骤，然后将其应用到工程实际中进行分析，结果证明了该方法的有效性和可行性。

1 MMC工作原理

图1 三相MMC拓扑结构Fig.1 Topological structure of three-phase MMC

图1是三相MMC拓扑结构[11-13]，由6个桥臂组成，上、下2个桥臂构成一相，每个桥臂由N+n个功率子模块（SM）和1个桥臂电抗器Ls级联而成，其中N为正常工作时的子模块数量，n为冗余子模块数量。图中a、b和c表示MMC的交流进线端，udc表示直流侧电容总电压。子模块的拓扑结构如图2所示，由2个绝缘栅双极型晶体管（IGBT）VT1和VT2、2个反并联二极管VD1和VD2以及1个直流电容C组成。子模块存在3种基本工作状态：VT1导通和VT2关断的投入状态、VT1关断和VT2导通的切除状态、VT1和VT2同时关断的闭锁状态。MMC由多个子模块构成，如果有1个或多个子模块发生故障，将会严重影响MMC的正常运行，冗余模块的配置能够解决这一问题。当某个工作子模块发生故障时，通过开关将其旁路后投入冗余模块，代替其工作，避免了系统停运，提高了系统可靠性和工作效率。

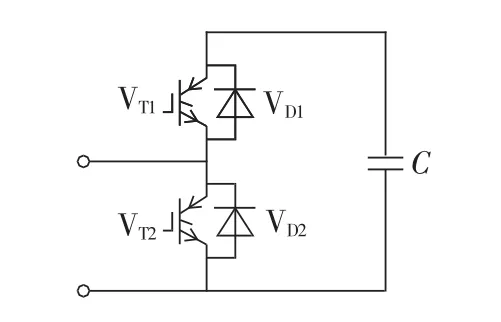
图2 子模块拓扑结构Fig.2 Topological structure of sub-module

2 模块冗余保护方案

模块冗余保护能否提高系统可靠性的关键在于：将故障模块切换到冗余模块的速度以及冗余模块投入后系统的运行状态。根据这2点，目前主要有3种模块冗余保护方案，将其简称为：冷备用运行、热备用对称运行和热备用非对称运行。

冷备用运行方案[14]：当系统正常工作时，冗余模块被旁路，不参与运行；当模块发生故障时，故障模块被旁路，冗余模块投入运行。该方案从故障模块切换到冗余模块时间较长，需要额外的电容充电时间，延长了动态过程，但冗余模块投入后系统的运行状态与故障之前完全相同。

热备用对称运行方案[15]：当系统正常工作时，通过子电容电压排序法选择工作的模块，这时所有模块都参与排序。当模块发生故障时，将故障模块旁路，同时也将其他桥臂切除相同数量的模块，剩余模块同样采用子电容电压排序法选择是否处于工作状态。该方案从故障模块切换到冗余模块时间较快，冗余模块投入后系统处于对称运行状态，不会影响环流，但是大量正常模块的切除既降低了系统可靠性，又不经济实用。

热备用非对称运行方案[16-17]：当系统正常工作时，通过子电容电压排序法选择工作的模块，这时所有模块都参与排序。当模块发生故障时，将故障模块旁路，其他桥臂保持不变，这样每个桥臂的模块数量不同，使得系统结构不对称。但是，通过分析可以发现：当故障模块数量小于等于冗余模块时，仍然可以保证每相上、下2个桥臂直流电压不变，不会引起较大环流，虽然结构不对称，但是运行依然是对称的。只有当故障模块数量大于冗余模块时，故障桥臂不能提供足够的直流电压，才会出现不对称运行情况。针对不对称运行，文献[18]提出了一种基于能量平衡的冗余容错控制策略，有效地消除了由桥臂不对称带来的环流问题，并通过仿真结果验证了该控制策略的有效性。冗余容错控制策略的提出解决了不对称运行带来的环流问题，为热备用非对称运行方案的应用奠定了理论基础。

基于对上述3种方案的总结，可知热备用非对称运行方案更加适合MMC系统。当故障模块数量小于等于冗余模块时，只需要切除故障模块即可，剩余的模块按照子电容电压排序法选择是否投入运行；当故障模块数量大于冗余模块时，切除所有故障模块，将剩余的模块都作为工作模块，并借助基于能量平衡的冗余容错控制策略来实现不对称运行。这样就可以既快速又可靠地实现模块冗余保护。

3 模块冗余配置方法

模块冗余配置是为了提高MMC系统的可靠性，冗余模块数量越多，系统的可靠性越高，但模块有效利用率较低，硬件成本较高，不经济，如何选取冗余模块数量将是一个十分有意义的课题。目前，相关研究较少，没有一种定量选取冗余模块数量的方案，大都是根据保守原则，结合工程经验和实际情况选择冗余子模块数量。为解决该问题，弥补技术上的缺陷，本文从MMC系统可靠性、冗余子模块有效利用率和冗余子模块数量3个方面出发，提出了一种基于多目标优化的MMC模块冗余优化配置方法。

3.1 方法步骤

模块冗余优化配置方法主要是从MMC系统的可靠性、冗余子模块有效利用和冗余子模块数量这3个目标出发，建立了多目标优化函数，并求解最优冗余子模块数量。在保证系统可靠性的前提下，可以有效节约成本，有助于系统的经济运行。图3是模块冗余优化配置方法流程图。

模块冗余优化配置方法步骤如下。

步骤1：确定MMC系统的可靠性RM。

首先，确定单个子模块的可靠性R，对于单个子模块只考虑IGBT、二极管和电容器，则可以得到单个子模块的可靠性 R[10]：

其中，R1为单个IGBT的可靠性；R2为单个二极管的可靠性；R3为单个电容器的可靠性。

然后，根据正常工作时的模块数量N和单个子模块的可靠性R，可以得到a相上桥臂的可靠性Ra1：

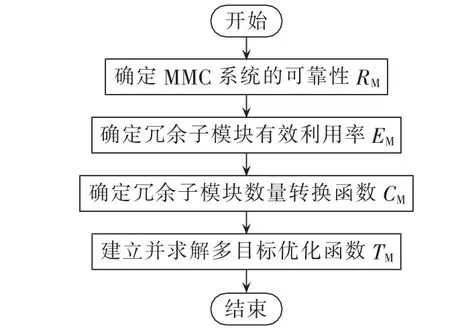
图3 模块冗余优化配置方法流程图Fig.3 Flowchart of optimal modular redundancy configuration

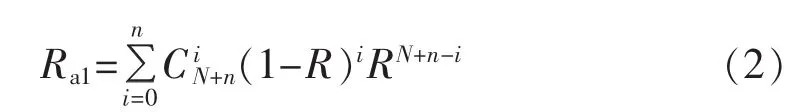
最后，假设MMC系统的可靠性RM只与单个子模块的可靠性R有关，其他设备暂不考虑，则可以得到 MMC 系统的可靠性 RM[10]：

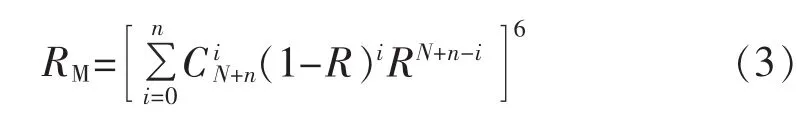
步骤2：确定MMC系统冗余子模块有效利用率EM。

首先，借助a相上桥臂可靠性Ra1的计算思想，得到a相上桥臂冗余子模块有效数量：

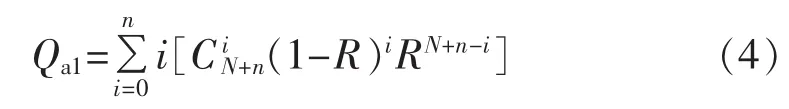
然后，同理可以得到MMC系统的冗余子模块有效数量QM：

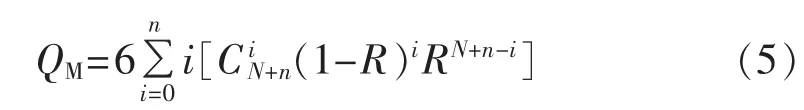
最后，根据冗余子模块数量n，可以得到MMC系统的冗余子模块有效利用率EM：

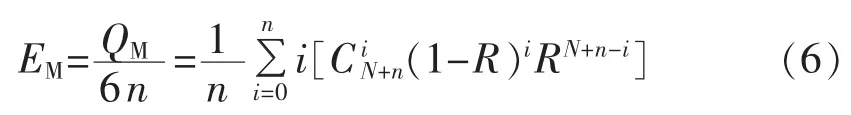
步骤3：确定冗余子模块数量转换函数CM。

首先，冗余子模块数量n的目标为在满足高可靠性的前提下，冗余子模块数量n越小越好，即：

然后，为了便于多目标优化问题的统一求解，将其转换到[0，1]，转化公式为：

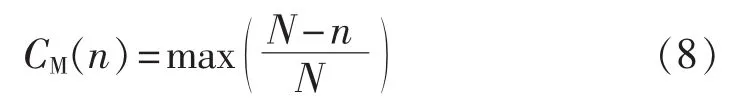
步骤4：建立并求解多目标优化函数TM。

首先，建立系统可靠性、冗余子模块有效利用率和冗余子模块数量的多目标优化函数：

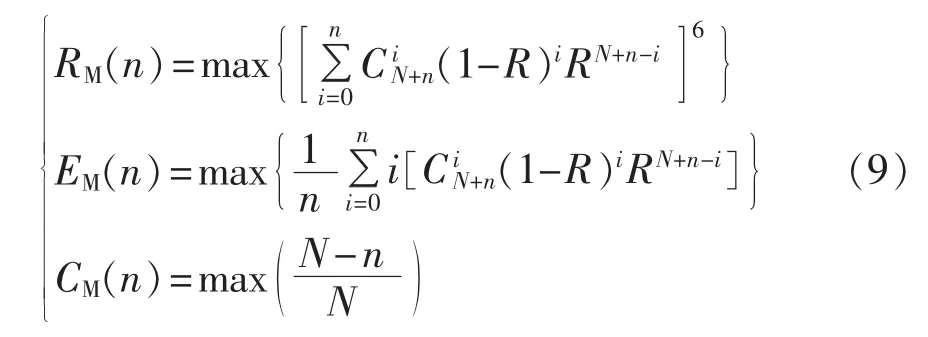
然后，求解多目标优化函数。求解方法1为求解3个目标值的共同最优结果。引入权值系数w1、w2和w3，将3个目标函数统一为一个目标函数：

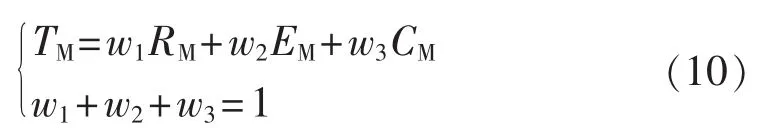
求解方法2为在保证高可靠性的前提下，尽可能地提高冗余子模块有效利用率和降低冗余子模块数量。则可以得到基于冗余子模块有效利用率和冗余子模块数量的目标函数：

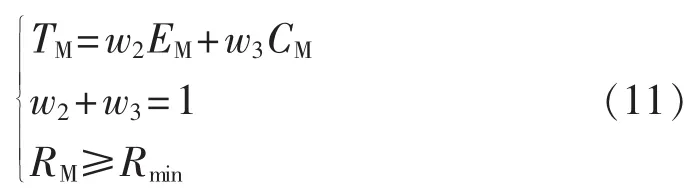
其中，Rmin为系统要求的最低可靠性。

3.2 方法结果

针对求解方法 1，根据式（9）和（10）可以计算得到冗余子模块数量。图4是MMC系统的可靠性RM、冗余子模块有效利用率EM、冗余子模块数量转换函数CM和目标函数TM随冗余子模块数量n的变化曲线。其中，假定 N=100，R=0.98，w1=0.6，w2=0.2，w3=0.2（对于工程实际，N 和 R 必然是确定的，w1、w2和w3是由系统可靠性和硬件成本权衡得到的，需要根据工程实际设定，可以在一定范围内选择）。显然系统可靠性RM和冗余子模块数量转换函数CM都是单调函数，而冗余子模块有效利用率EM并非单调函数，是存在最大值的，同时目标函数TM也是存在最大值的，其最大值所对应的冗余子模块数量即为最优冗余子模块配置数量。

图4 RM、EM、CM和 TM随 n 的变化曲线Fig.4 Curves of RM，EM，CMand TMvs.n

图5是目标函数TM在不同w1、w2和w3参数下随n的变化曲线。显然w1、w2和w3参数不同时，目标函数TM曲线存在较大差异，对应的最大值，即最优冗余子模块配置数量也不相同，从而证明w1、w2和w3参数的选取十分重要，需要权衡系统可靠性和硬件成本，根据工程实际情况选择得到。

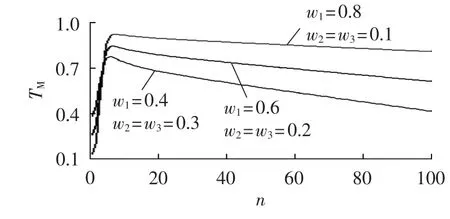
图5 TM在不同参数下随n的变化曲线Fig.5 Curve of TMvs.n for different parameters

在实际工程应用中，不可能根据不同情况每次都来计算一次冗余子模块配置数量，因为这将会浪费大量时间。为了方便使用和查找，可以将其制作成模块冗余配置手册，用户只需提供 N、R、w1、w2和 w3，就可以查表得到最优冗余子模块配置数量。表1作为范例，给出了当 R=0.98、w1=0.6、w2=0.2、w3=0.2 时，最优冗余子模块数量n与N的关系表格。

表1 最优冗余子模块数量与N的关系Table 1 Relationship between optimal quantity ofredundant sub-module and N

但是，实际工程应用中，有时很难权衡系统可靠性和硬件成本来得到定量的权重关系，只需在保证可靠性的前提下，尽可能地提高冗余子模块有效利用率和降低冗余子模块数量，这时求解方法2就可以得到较好的应用。考虑到冗余子模块有效利用率和冗余子模块数量的相关性较大，为了进一步简化，令w2=w3=0.5。图6是最优冗余子模块数量n在不同Rmin下随正常工作模块数量N的变化曲线。显然参数Rmin不同时，n差异较大，因此系统要求的最低可靠性Rmin选取也至关重要，影响着最优冗余子模块数量的选择，和实际情况十分相似，进而证明了该方法的有效性和可行性。

图6 n在不同Rmin下随N的变化曲线Fig.6 Curve of n vs.N for different Rminvalues

同理，为了便于工程实际应用和用户查找，可以将其制作成模块冗余配置手册，用户只需提供N、R和Rmin，就可以查表得到最优冗余子模块配置数量n及其对应的系统可靠性RM。表2作为范例，给出了当 R=0.98、Rmin=0.99 时，最优冗余子模块数量 n 与 N的关系表格。

3.3 方法分析

前面详细介绍了模块冗余配置方法的步骤和结果，下面将以正常工作时子模块数量N=50为例进行分析，验证该方法的有效性和优越性。为了更加清楚地说明问题，文中又引入了冗余度σ[9]和可靠性增长率g 2个概念，具体定义为：

表2 最优冗余子模块数量与N的关系Table 2 Relationship between optimal quantity ofredundant sub-module and N

其中，0≤n≤N，则 0≤σ（n）≤1，0＜g（n）＜1。

表3为 R=0.98、N=50时 σ 和 RM随 n值的变化表。显然随着冗余度σ的增加，系统可靠性RM也逐渐增加，但冗余模块数量的增加，必然带来成本的增加，降低冗余模块的有效利用率，造成较大的浪费。当N=50时，通过本文提供的方法得到最佳冗余模块数量为 5，对应的 RM为 0.9952，σ 为 0.10，可靠性高，冗余度低，进而验证了该方法计算冗余模块数量的可行性。

表3 σ和RM随n值的变化Table 3 σ and RMfor different n values

图7为可靠性增长率g随冗余模块数量n的变化曲线。显然可靠性增长率g（n）始终是大于0的，可知系统可靠性随着冗余模块数量n的增加而增加。分析该图可以发现：n=5是该曲线的转折点，当n≤5 时，可靠性增长率 g（n）较大，都大于 0.01，表明每增加1个冗余模块，将极大提高系统的可靠性，这时通过增加冗余模块数量来提高系统可靠性是十分有效的，可以在提高系统可靠性的前提下，尽量增加冗余模块数量；而当n＞5时，可靠性增长率g（n）较小，远远小于0.01，甚至接近于0，表明每增加 1个冗余模块，系统可靠性提高很少，几乎可以忽略，这时通过增加冗余模块数量来提高系统可靠性就变得没有意义了，进而表明n=5是最优结果，也验证了该方法计算冗余模块数量的有效性。

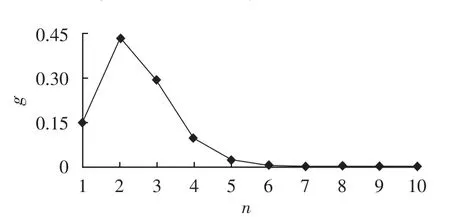
图7 g随n的变化曲线Fig.7 Curve of g vs.n

目前，没有一种具体、有效的方法来选择冗余模块数量，一般是通过实际工程经验得到的，但是很难综合考虑各种因素快速得到最优冗余模块数量。通过本文提供的方法，综合考虑系统可靠性、冗余子模块有效利用率和冗余子模块数量3个因素，建立多目标优化函数，利用目标函数最优值来确定冗余模块的数量。这里假设目标函数形式如式（10）中TM所示，并令 w1=0.6、w2=0.2、w3=0.2，则可以得到目标函数 TM随n值的变化结果如表4所示。显然n=5时，目标函数值最大，对应的冗余模块数量最优；当n＞5时，不仅目标值显著减少，而且冗余模块数量的增加提高了硬件成本；当n＜5时，尽管冗余模块数量少，但是系统可靠性不高。综上所述，n=5是综合考虑3个因素的最优结果。通过本文提供的方法，采用查表操作无需额外的计算，就可以快速、有效地得到最佳冗余模块数量，大幅减少了工程设计人员的工作，提高了工作效率，进而验证了该方法计算冗余模块数量的优越性。

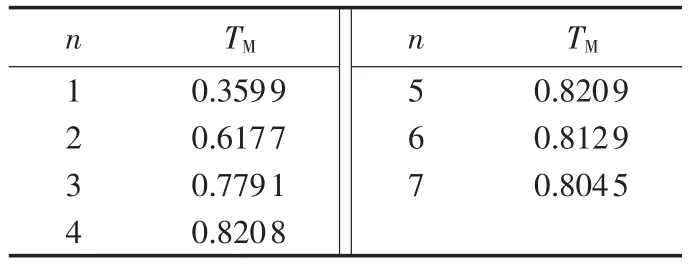
表4 TM随n值的变化Table 4 TMfor different n values

4 仿真分析

为了验证本文所提出的模块冗余配置方法的有效性和可行性，在PSCAD／EMDTC中搭建了基于MMC的11电平仿真模型，其中模块冗余保护方案采用热备用非对称运行方式，模型参数如下：交流电压有效值为380 V，直流母线电压为900 V，桥臂子模块数量为10，子模块电容电压为90V，桥臂电抗器为5mH，开关频率为2 kHz。

采用本文所提出的模块冗余配置方法计算冗余子模块数量，2种方法计算结果都为2，因此将配置2个冗余子模块。根据本文所提出的方法，设定单个子模块可靠性R=0.98，则该系统有1个模块故障的可能性为0.3431，某一相同时有2个模块故障的可能性为0.0385，某一相同时有3个模块故障的可能性为0.0026，显然3个及以上模块故障的可能性极小，冗余模块数量设置为2是比较合理的，这样在保证系统高可靠性的前提下，有效减少了模块数量，降低了硬件成本，从而也验证了配置方法的有效性。考虑到有1个模块故障的可能性较大，因此本文设定1个模块故障。具体故障设置：0.1 s时向电网注入100 A无功电流；0.25 s时a相上桥臂1个模块故障，此时封锁该模块的控制信号，并控制旁路开关闭合；0.26 s时旁路开关闭合，进入正常的工作状态。仿真中的电压、电流波形如图8、9所示。

图8 电压量仿真波形Fig.8 Simulative voltage waveforms

图8为电压量仿真波形。显然0.25 s之前，MMC基本工作于稳定状态，直流母线电压稳定在900 V左右，三相电容电压趋于稳定，平均值在90 V左右波动。在此阶段里，有9个模块始终处于工作状态，1个模块始终处于冗余状态，而剩余2个模块工作状态发生了互换，一个从工作状态切换到冗余状态，而另外一个从冗余状态切换到工作状态（如图8（d）所示），这样就保证了每个桥臂12个模块中，始终有10个模块处于工作状态，另外2个模块处于冗余状态，从而保证系统处于对称运行状态，验证了热备用非对称运行方案的正确性。0.25 s时a相上桥臂有1个模块故障，此时封锁该模块的控制信号，并控制旁路开关闭合，由于故障模块故障前处于工作状态，将其闭锁后处于工作状态的模块数量将减少1个，为了保证系统的对称运行，必须将处于冗余状态的模块切换到工作状态（如图 8（d）和 8（f）所示）。同时在旁路开关闭合前，会对故障模块电容进行充电，使得a相桥臂能量发生变化，而b、c相桥臂能量基本保持不变，这样就会造成直流母线电压和a相电容电压平均值发生一定波动，b、c相电容电压平均值基本不变。0.26 s时旁路开关闭合，故障模块被旁路，电容电压保持不变，系统进入正常运行状态，此时直流母线电压和三相电容电压平均值也迅速到达稳定状态，从而完成了故障模块的切换。

图9为电流量仿真波形。显然整个过程中三相输出电流高度正弦化，幅值为100 A，基本保持不变，故障对输出电流影响较小，避免了对电网的干扰，提高了系统可靠性。而a相上、下桥臂电流故障时存在一定波动，但故障切除后又迅速回到稳定状态。前面分析了1个模块故障的情况，当有2个模块故障的情况与其类似，不再赘述，当有3个及其以上模块故障的情况，可能性很小，且系统运行于不对称状态，不属于本文研究的重点，故不再叙述。

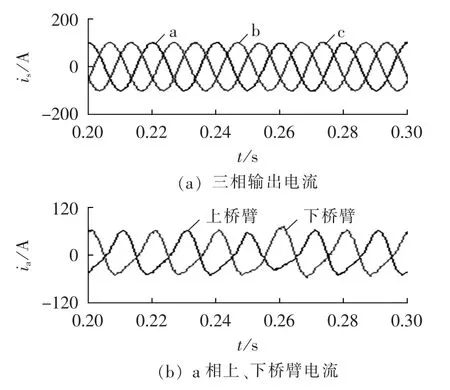
图9 电流量仿真波形Fig.9 Simulative current waveforms

综上所述，本文所提出的冗余模块配置方法简单、有效，在保证系统高可靠性的前提下，能够极大优化模块数量，减少硬件成本。同时配合热备用非对称模块冗余保护方案，不仅能够快速完成故障模块的切换，而且对直流母线电压、三相电容电压平均值和三相桥臂电流等系统参数影响较小，保证了输出波形质量，避免了系统停运，提高了系统可靠性和工作效率。