采用不同子模块的MMC-HVDC阀损耗通用计算方法
2015-09-19薛英林张哲任刘高任
薛英林,徐 政,张哲任,刘高任
(浙江大学 电气工程学院,浙江 杭州 310027)
0 引言
2001年,德国慕尼黑联邦国防军大学的学者R.Marquardt首先提出了模块化多电平换流器MMC(Modular Multilevel Converter)拓扑[1],该拓扑 的桥臂采用基本运行单元级联的形式,避免大量开关器件直接串联,不存在动态均压和一致触发等问题,尤其适用于高压直流输电场合[2-10]。后来,R.Marquardt又在2010年和2011年的2次国际电力电子会议上提出广义MMC的概念[11-12],以子模块为功率单元,并根据内部构造不同将其分为3种基本类型:半桥子模块 HBSM(Half Bridge SubModule)、全桥子模块FBSM(Full Bridge SubModule)和箝位双子模块CDSM(Clamp Double SubModule)。 为简化分析,本文将子模块采用HBSM、FBSM和CDSM的MMC相应地称为H-MMC、F-MMC和C-MMC。
阀损耗是直流输电系统稳态运行损耗的主要组成部分,其大小是评估其性能优劣的重要指标。损耗计算一方面能为开关器件选型、散热系统设计[13]和经济效益评估提供理论依据,另一方面也能为后续拓扑结构优化和降损措施研究[14-15]奠定基础。目前关于传统两电平换流器损耗的研究较为完善[16-17],但缺乏适用于不同子模块的MMC通用损耗计算方法和损耗特性的定量对比。
一般地,适用于工程实际的换流器损耗评估手段或建模应满足以下基本要求:计及控制调制策略,真实反映系统运行特性;有效提取IGBT器件参数,合理拟合其损耗曲线;计算快速,结果准确。MMC的电气运行工况非常复杂,因此很难用直接的电气测量方法实现损耗测量。现有损耗计算方法主要分为2 类:解析公式法[18-20]和仿真积分法[21-22]。 解析公式法通过引入电流平均化概念,推导了子模块各器件平均电流的解析公式,计算简便快速,适用于损耗初步评估;但该方法无法体现MMC非线性调制特性,难以有效计及附加平衡控制引起的开关损耗,同时也无法得到桥臂各子模块损耗分布特性。一般降损措施主要针对开关过程引起的暂态损耗如开通损耗和关断损耗,因此仅依靠解析公式不能有效评估降损策略带来的效益。仿真积分法通常需要在仿真软件如 PSCAD/EMTDC、MATLAB/Simulink 等平台上搭建完整的系统模型和复杂的控制系统,借助实时仿真特性曲线计算运行损耗,可计及各种控制特性且计算结果精确;但该方法仿真步长较小、计算时间长,不适合多工况计算,特别在系统规划初期阶段,可能需要多次迭代计算,该方法难以胜任如此巨大的工作量。因此,研究MMC阀损耗评估模型并开发快速通用计算方法,具有重要工程意义。
为此本文提出一种阀损耗通用计算方法,可以适用于H-MMC、F-MMC和C-MMC。本方法首先根据系统基本运行工况和主回路参数计算出桥臂电流;然后利用最近电平调制和子模块优化平衡控制策略,根据子模块内部结构特点,计算出各子模块开关状态和相关电气量如内部器件电流、电容电压;通过提取IGBT厂家数据进行数据拟合来建立IGBT开关损耗模型;在给定参数下统一进行损耗评估和求解。基于本文方法开发了MMC型高压直流输电系统(MMC-HVDC)阀损耗分析程序,可计算各种工况下的换流器功率损耗和器件结温分布,为后续降损设计提供了有力工具。最后通过一个算例验证本方法的有效性,并定量分析和对比不同典型结构下的损耗特性。
1 MMC结构特点和子模块开关函数模型
如图1所示,MMC拓扑结构采用三相六桥臂结构,每桥臂由N个基本运行功率单元级联而成,同时配置一个缓冲电抗L0以抑制环流和故障电流上升率。Udc为MMC双极直流母线电压差。

图1 MMC通用拓扑结构Fig.1 General topological structure of MMC
根据内部结构不同,子模块分为HBSM、FBSM和CDSM,分别如图 2(a)— (c)所示。 HBSM 由 2 个IGBT(VT11、VT12)、2 个反并联二极管(VD11、VD12)和直流电容C组成;子模块输出电压USM有0和UC这2种电平,其中UC为额定电容电压。FBSM需要的开关器件数量是HBSM的2倍,但输出电平有3种:-UC、0和UC。CDSM由2个等效半桥单元通过2个箝位二极管和1个引导IGBT(VT0)构成。正常运行时VT0一直导通,CDSM等效为2个级联的半桥子模块,因此输出电平有3种:0、UC和2UC。这样每桥臂N个CDSM的C-MMC可移植每桥臂2N个HBSM的H-MMC的控制策略。根据实际应用场合特点和直流系统故障穿越需求不同,MMC选取不同子模块作为基本功率单元。其中H-MMC所需开关器件最少且运行损耗最低,但是存在二极管续流效应而无法有效处理直流故障,因此一般用于电缆敷设线路场合[23-24];F-MMC和C-MMC所需开关器件和稳态运行损耗均大于H-MMC,但具有直流故障自清除能力,所以可以应用在架空线输电场合[25-27]。
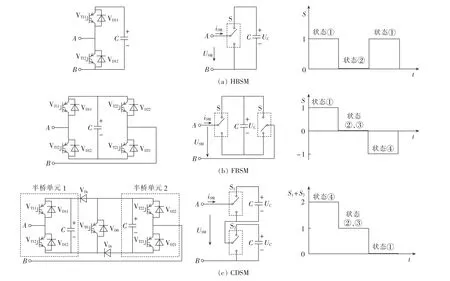
图2 不同模块拓扑结构和开关模型Fig.2 Topological structure and switching model of different submodules
如图2所示,定义子模块电压和子模块电流正方向均为从A点到B点,反之则为负。定义电容开关函数S如式(1)所示,用以描述子模块电容的投切状态。S=1表示正投入模块电容,即USM=UC;S=0表示切除(或旁路)模块电容,即USM=0;S=-1表示负投入模块电容,即USM=-UC。USM为子模块输出电压。S1、S2分别表示CDSM中半桥单元1和半桥单元2的开关函数。

子模块电容电压由下式描述:

其中,下标m取p、n分别表示上、下桥臂,j表示子模块电容编号,下同;C为模块电容。
相关IGBT的控制信号与电容开关函数状态、子模块电压的关系如表1所示。
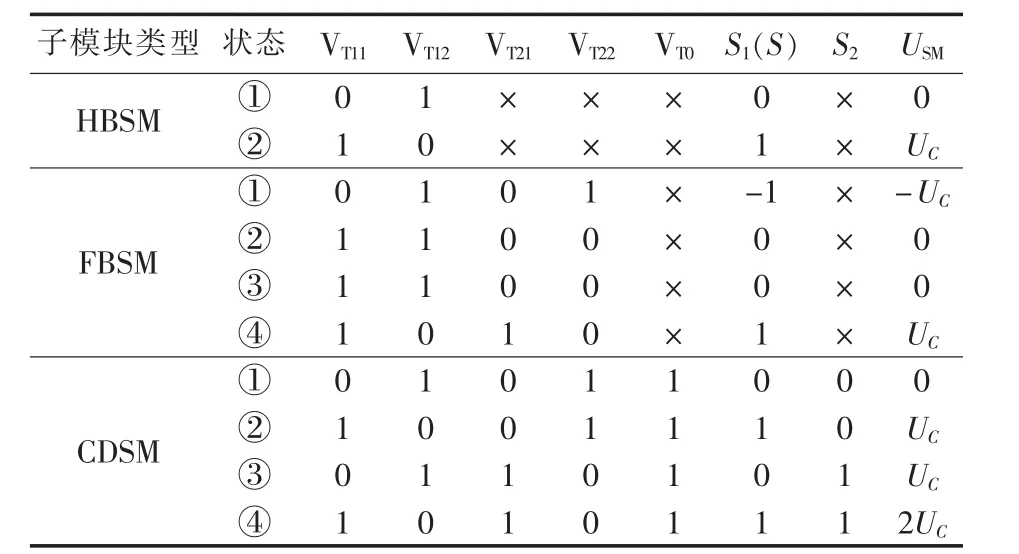
表1 子模块开关函数状态和IGBT控制信号Table 1 State of submodule switching function and control signal of IGBT
2 主回路参数和子模块电气量计算
2.1 主回路参数计算
MMC单相接线图如图3所示,忽略回路中阻性成分,各电气量正方向如图中箭头所示。根据电路原理,求解交流相电流Iv和MMC交流侧虚拟对地电势Uv:

其中,P、Q分别为交流侧有功、无功功率(一般作为运行工况的最原始参数);Ls为系统电感;L0为桥臂电感;Us为折算到换流变阀侧的系统电压,上标星号表示取共轭运算。
忽略换流器损耗,求解直流电流:
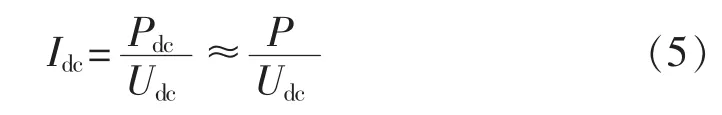
假设电网电压us写成如下形式:
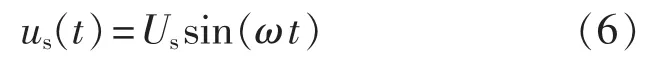

图3 MMC单相等效电路Fig.3 Single-phase equivalent circuit of MMC
则根据式(3)和(4)得相电流 iv和虚拟出口电压uv:

上、下桥臂级联电容电压up、un为:
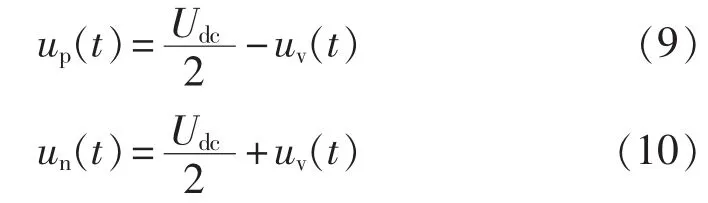
上、下桥臂电流 ip、in分别如式(11)、(12)所示。λ=1说明未采取环流抑制措施;λ=0说明采取环流抑制措施。
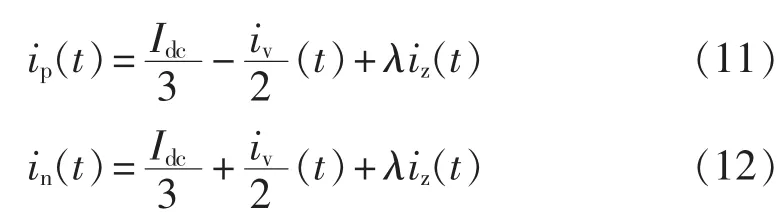
其中环流分量主要为2次谐波,写成如下形式[28]:

2.2 最近电平调制和子模块优化平衡控制
调制策略决定着子模块电容的投切时刻,影响半导体器件的开断电压和开关频率,进而影响其开关能量和损耗。采用传统的解析公式或面积等效法[29]计算损耗,均无法考虑附加电容平衡控制带来的附加切换情况,对于开关损耗计算通常依靠人为设定投切频率(如150 Hz)来估算。此外,系统采样频率可能会对子模块投切造成影响[30],但在传统解析计算中无法反映。本节所述方法能够计算子模块电容开关时域特性曲线,可计及调制策略、附加平衡控制和采样频率等因素影响。
调制的目的就是选择投切特定数目的子模块使之逼近调制参考波,调制策略很多,如载波移相调制、空间矢量调制、最近电平逼近调制等。由于实现简单,最近电平逼近调制适合于采用数百子模块的高压直流输电系统,其主要思想是通过阶梯波去逼近参考电压。每时刻子模块电容投切数目通过对桥臂电压参考波进行取整运算求得,如式(16)所示。每个时刻上、下桥臂中需要正投入的子模块电容恒定如式(17)所示。

其中,[x]表示取与变量x最接近的整数。值得说明的是,为便于统一不同子模块下的表达式,上式选用电容投切数而不是子模块投切数为控制对象。对于CDSM而言,模块电容数目是子模块数目的2倍。
子模块电容相应的开关状态满足式(19):
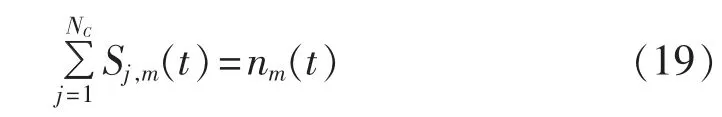
选择子模块电容投切的基本原则为:在采样时刻,当桥臂电流为负时优先选择电压高的电容放电,当桥臂电流为正时优先选择电压低的电容充电,如式(20)所示。
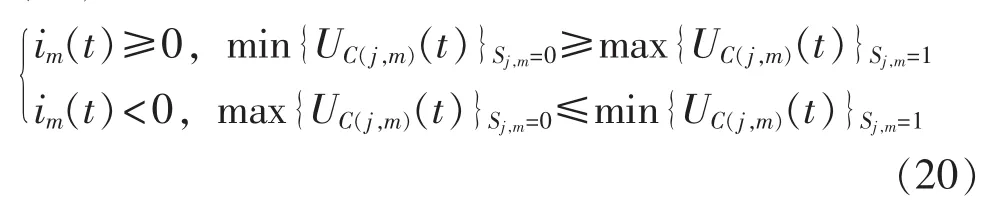
优化平衡控制策略有2种基本方法:一是通过改变调制波以改变子模块电容充放电时间[31],此方法适用于脉宽调制场合;二是通过引入电容电压最大偏差量[14]或保持因子[15]优化子模块电容投切时刻。本文采用文献[14]所述优化策略。根据以上原则确定HBSM和CDSM模块电容开关函数的时域特性曲线。
FBSM控制自由度较多,因此仅依靠式(20)不能完全确定其开关函数。为此,本文采取输出负电平数最小原则,这样只有在电压调制比大于1的情况下才会有负电平出现。

其中,N+为正投入的模块电容数;N-为负投入的模块电容数;N0为切除的模块电容数。
2.3 子模块器件电流、电压求解
利用上节确定各模块电容的开关函数,可以求解子模块内各器件的电流时域特性曲线。子模块电容电流写成如下形式:

在[τ,τ+Δt]区间内,基于式(2)利用离散积分法求解电容电压:

为便于后续分析开关器件电流,定义函数如下:
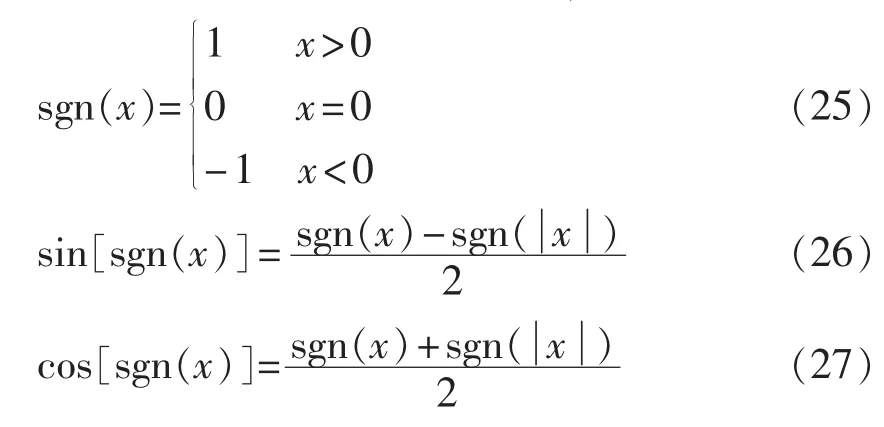
2.3.1 HBSM 的开关器件电流
根据图2、半导体器件开关特性和开关函数定义,HBSM的开关器件通过电流可写成如下形式。
IGBT VT11上的电流为:

2.3.2 FBSM 的开关器件电流
当子模块输出电平为零时,事实上有2种工作状态,本文选取电流均经过下部开关器件的状态,这样 iVT11、iVD11、iVT12和 iVD12电流表达式与 HBSM 一致,其余器件电流由式(32)—(35)确定。
IGBT VT21上的电流:


2.3.3 CDSM的开关器件电流
正常运行时,CDSM的阻尼二极管不存在电流通路。单个CDSM等效为2个HBSM来处理,VT0/VD0近似一个串联的通态电阻,器件电流仅与桥臂电流方向相关。

根据以上公式,可以求出不同子模块开关函数波形和器件电流波形,其波形示意如图4所示(此时假设F-MMC不考虑输出负电平,零电平状态选择为电流均经过下部开关器件的状态)。
图4 子模块开关函数和器件电流波形示意Fig.4 Waveform of submodule switching function and device current
3 开关器件参数提取和损耗建模
MMC阀损耗计算最终分解为各个开关器件(IGBT及其反并联二极管)的损耗计算。稳态运行下IGBT器件的功率损耗主要有以下3个部分[16]:通态损耗 Pcon,VT、开通损耗 Pon,VT和关断损耗 Poff,VT。IGBT的正向截止损耗和驱动回路损耗在总的损耗所占比例较少,一般忽略不计。

IGBT的反向并联二极管运行损耗主要包括通态损耗 Pcon,VD、开通损耗 Poff,VD、恢复损耗和截止损耗,其中后两者损耗分量可以忽略。故二极管损耗写成:

因此将MMC所有开关器件损耗进行叠加即可求得阀损耗:

其中,下标VT表示IGBT部分;下标VD表示反并联二极管部分。
3.1 损耗计算
3.1.1 器件通态损耗计算
IGBT和二极管的正向导通电压主要与导通电流和结温有关:

其中,UVT0、RVT分别为IGBT擎住电压和正向导通电阻;UVD0和RVD分别为二极管门槛电压和正向导通电阻。这4个特性参数均与结温Tj有关,可利用结温Tα和 Tβ(一般 Tα=25℃ ,Tβ=125℃)下开关器件的典型特性曲线,通过参数插值近似得到:

通过曲线拟合得到给定结温Tj下的开关器件特性参数后,利用式(45)和(46)求取IGBT和二极管的通态损耗:

其中,Tc为一个基波周期,即0.02 s。
3.1.2 器件开关损耗计算
给定电流和结温,半导体器件的开关能量损耗可用如下二次多项式进行拟合:
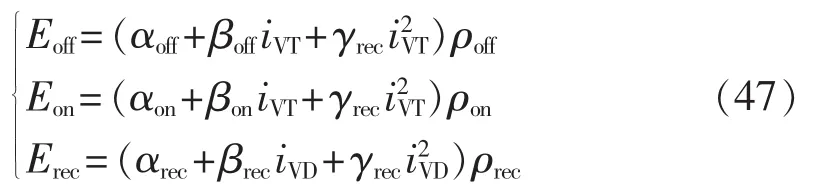
其中,α、β、γ为在给定参考电压和结温下开关能量损耗的拟合系数;ρ为开关能量损耗函数的修正系数;下标off、on和rec分别对应IGBT关断损耗、IGBT开通损耗和二极管的恢复损耗。
使用线性插值方法,求得折算到给定截止电压和结温下的修正系数 ρ[16]。

其中,ρoff、ρon和 ρrec分别为 IGBT 的关断损耗、IGBT的开通损耗以及二极管的反向恢复损耗;UVT_ref和UVT分别为参数表上的参考截止电压以及实际运行中的真实截止电压。
将一个基波周期内开关能量损耗进行累加,然后对其进行时间平均,即可获得各部分的平均开关损耗功率:

其中,Nα、Nβ、Nγ分别为 IGBT 关断次数、IGBT 开通次数和二极管反向恢复次数。
3.2 结温估计
IGBT器件内部的结温无法直接测量得到,因此可依据散热器的温度和以上损耗计算结果估计IGBT模块内部的器件结温。IGBT等值热电路模型如图5所示,IGBT和二极管的功率损耗等值为2个电流源,估算公式如下[21]:
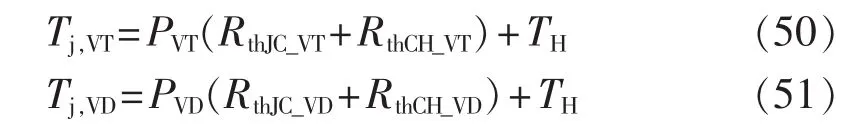
其中,RthJC_VT、RthJC_VD分别为IGBT、二极管的 PN结与器件外壳之间的热电阻;RthCH_VT、RthCH_VD分别为IGBT、二极管的器件外壳与散热器之间的热电阻;TH为散热器温度。
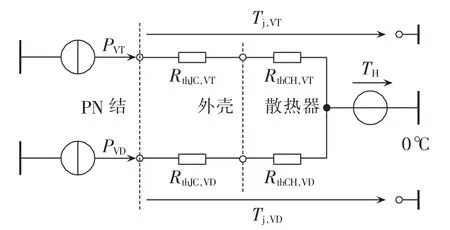
图5 IGBT模块等值热电路模型Fig.5 Equivalent thermal model of IGBT module
4 计算流程与步骤
MMC-HVDC换流阀损耗计算流程如图6所示,主要分为以下6步:
a.基于系统运行基本条件(P,Q,Us,Udc)和主回路参数(Ls,L0,C,N),根据式(1)— (15)计算换流器交流侧相电流、桥臂电流和桥臂电压在基频周期[0,Tc]内的时域特性曲线;
b.选择子模块类型,根据最近电平调制和附加电容电压优化平衡策略,并计及采样频率的影响,利用式(16)—(21)求解各个子模块电容的开关函数时域特性曲线;
c.根据桥臂电流和子模块电容开关函数,由式(22)—(37)求解子模块各半导体器件的电流时域曲线;
d.根据选定型号的IGBT和二极管的特性曲线(厂家提供的器件特性数据),应用曲线拟合法得到式(41)、(42)和(47)所需的各项器件特性参数,设置初始结温Tj,然后利用线性插值修正相关系数,如开关能量损耗的温度系数、IGBT和二极管的正向导通电压或通态电阻等;

图6 损耗通用计算流程Fig.6 Flowchart of general loss calculation
e.将IGBT和二极管上的电压、电流、结温等数据代入式(45)、(46),求得器件的导通损耗功率,并根据触发脉冲,判断器件的开关动作,由式(49)对导通损耗和开关损耗在一个周期内做平均,可得到平均损耗功率,然后根据式(38)—(40)计算给定运行工况下的阀总损耗,根据式(50)、(51)估计子模块的器件结温;
f.若需要计算其他运行工况,则重复步骤a—e,否则计算结束。
5 性能评估和仿真分析
基于第4节所述流程,在MATLAB中编写M文件代码开发了通用计算程序,可以方便地评估环流、电容电压附加控制等各种因素对损耗的影响,快速计算各种运行工况下的损耗。下面通过一个算例来验证本方法的有效性。
算例系统的主回路参数如下:直流系统额定直流电压为±160 kV,额定功率为320 MW;交流系统电压等级为110 kV,系统电抗为10 mH,换流变压器变比为110 kV/167 kV,换流变压器容量为350 MV·A,换流变压器漏抗为0.1 p.u.,电压调制比为0.85;换流器每桥臂电容数为200,子模块额定电容为24500μF,额定电容电压为1.6 kV;调制策略采用最近电平调制(文献[14]所述优化策略),最大电压偏差率σ(最大电压偏差和额定电压之比)为4%;IGBT采用Infineon FZ1200R33KF2C。
根据第3节所述曲线拟合方法对器件特性参数进行拟合,表2、表3分别给出了IGBT模块通态压降与通态电阻以及IGBT模块的开关能量损耗函数中的系数。IGBT模块热电阻选取厂商提供的典型参数:RthJC_VT=0.0085 K /kW,RthJC_VD=0.017 K /kW,RthCH_VT=0.006K /kW,RthCH_VD=0.012 K /kW。
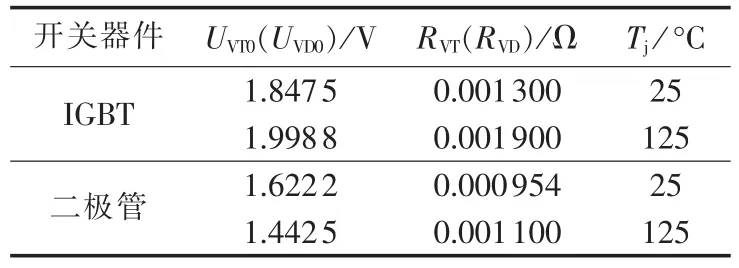
表2 IGBT模块通态压降与通态电阻Table 2 On-state voltage drop and on-state resistance of IGBT module

表3 IGBT模块的开关能量损耗函数中的系数Table 3 Coefficients of switching loss function of IGBT module
不失一般性,考察H-MMC、F-MMC和C-MMC随功率因数角变化的功率损耗,如图7(a)所示,变化过程中保持交流系统视在功率为320 MV·A且直流电压为320 kV不变。从图中可以看出,H-MMC损耗最小,总损耗在1.43~2.08 MW之间波动(阀损耗率约为0.45%~0.65%);C-MMC次之,总损耗在2.26~2.79 MW之间波动(阀损耗率约为0.70%~0.87%);F-MMC损耗最大,总损耗在2.97~3.50 MW之间波动(阀损耗率约为0.93%~1.09%)。在整流模式下MMC损耗整体略大于逆变模式下运行损耗。在考察的所有工况中,功率因数角处于小角度范围(22.5°~67.5°)内,MMC的损耗比较低。单位功率因数下子模块损耗分布特性如图7(b)所示。CDSM损耗接近于FBSM损耗,但是其子模块数是后者的一半,因此C-MMC的总损耗比F-MMC降低25%左右。
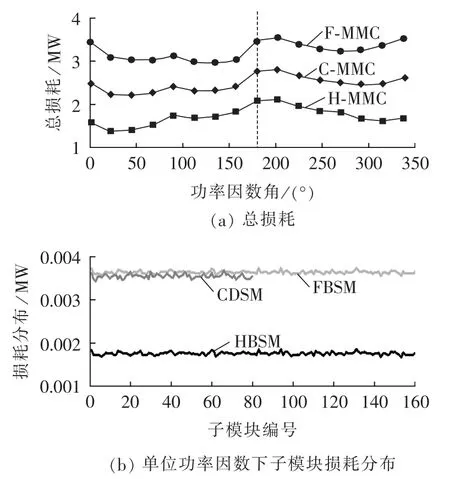
图7 损耗随功率因数变化特性和单位功率因数下子模块损耗分布Fig.7 Characteristic curve of loss vs.power factor and submodule loss distribution for unity power factor
本方法可以给出子模块各器件结温分布(环境温度TH=26.7°C),如图8所示。由于子模块投切时刻不同,产生的损耗不同,故结温也不完全相同,但在一定范围内波动。子模块内各器件损耗和结温分布不均衡,以HBSM为例,二极管VD12结温最高,IGBT VT12结温最低,其主要原因在于前者通流时间长(如图4所示)。

图8 单位功率因数下不同子模块内各器件的结温分布Fig.8 Submodule junction temperature distribution for unity power factor
图9(a)展示了环流对损耗的影响。从结果来看,环流抑制后大部分工况下换流器损耗特性得以改善,但在个别工况下反而可能恶化,如图中阴影部分内的工况。其原因在于环流分量影响了桥臂电流的波形,进而改变了桥臂电流在IGBT和二极管的分配比例,由于二者的通态压降和通态电阻不一样,故产生的损耗不同。
优化电容电压平衡控制策略中,子模块最大电容电压偏差率越大,器件的开关频率越小,从而损耗越小,如图9(b)所示。从降损角度看,应选择较大的子模块最大电容电压偏差率,但过大可能引起子模块电容不能充分充放电,出现电压不平衡。
高电压调制比可降低MMC阀侧交流电流,进而降低器件的通态损耗,如图9(c)所示。后续研究将考虑3次谐波注入调制,以期取得更高的电压调制比。
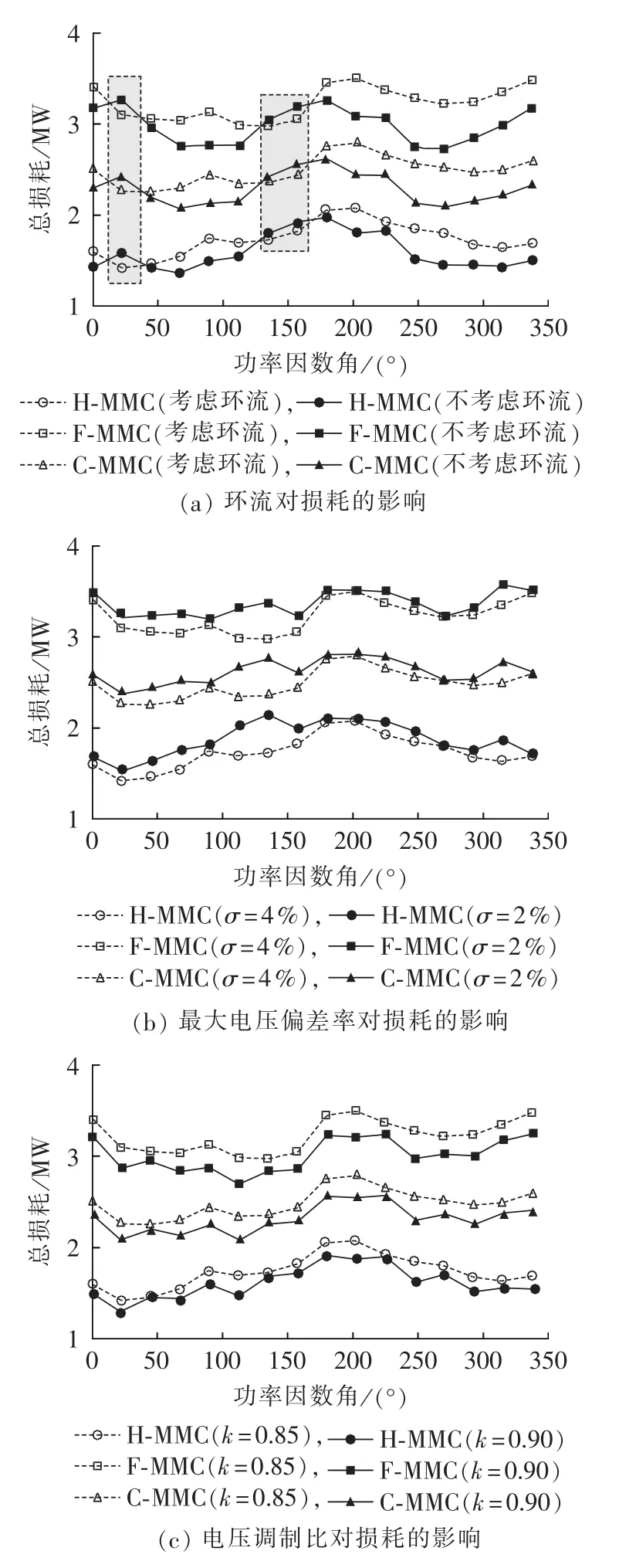
图9 环流、最大电压偏差率和电压调制比对损耗的影响Fig.9 Effect of circulating current,maximum voltage deviation or voltage modulation ratio on loss
为进一步分析器件开关频率与损耗之间关系,以H-MMC为例,单位功率因数下不同平均开关频率下换流器运行损耗如图10所示。从图中可以看出,随着器件开关频率下降,IGBT开关损耗和二极管关断损耗随之下降。对于本运行工况而言,当开关频率下降到500 Hz以下,通态损耗成为换流器总损耗的主导成分。因此,后续降损措施应该着重从如何降低器件通态电阻方面考虑,如选择低通态电阻的新型开关器件。
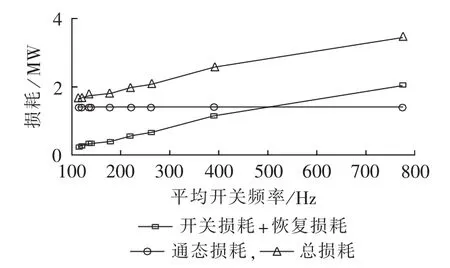
图10 H-MMC开关频率与运行损耗关系Fig.10 Relationship between switching frequency and operating loss of H-MMC
6 结论
在实际直流输电工程中,阀损耗计算的目的是为主电路参数设计提供各种工况和各种负荷水平下的各个器件损耗和结温数据,其结果将直接影响器件选型、元件定值确定和散热设计,因此对损耗进行既准确又快速的分析和计算十分必要。本文提出的方法适用于采用不同子模块结构的MMC拓扑,能够计及优化电容电压附加控制,所需特性参数可通过厂家提供的数据表拟合获得,因而具有很强的实用价值。基于本方法开发了MMC-HVDC阀损耗通用分析程序,可快速计算各种工况下的换流器功率损耗分布和器件结温。为验证本方法的有效性,对某算例进行分析和计算,并得到如下结论。
a.在子模块电容数相同的情况下,H-MMC损耗最少,C-MMC次之,F-MMC最差。由于通流时间不同,子模块内各器件的损耗和结温分布是不均匀的,故器件承受的热应力不同,所以在器件选型时需特别注意。
b.环流分量影响了桥臂电流的波形,进而改变了桥臂电流在IGBT和二极管的分配比例。然而由于IGBT和二极管的通态损耗特性不同,环流抑制后个别运行工况下换流器损耗特性可能恶化。
c.提高优化电容电压平衡策略中最大电压偏差率,可降低器件开关频率以减少器件的开关损耗;然而当器件开关频率低于某值(本算例为500 Hz)后,器件的通态损耗成为主导分量。因此进一步降损措施应着眼于如何降低其通态损耗。
d.提高电压调制比可降低MMC阀侧交流电流,进而降低器件的通态损耗。后续研究将考虑3次谐波注入调制,以期取得更高的电压调制比。
