双馈风电变流器IGBT模块功率循环能力评估

李 辉，秦 星，刘盛权，杨 东，杨 超，胡姚刚，冉 立，唐显虎

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.重庆科凯前卫风电设备有限责任公司，重庆 401121）

0 引言

风电变流器作为风能转换系统中的枢纽，是影响风电机组及其入网稳定性的重要环节，但现有文献表明，风电变流器是风能转换系统中的薄弱环节之一，因变流器失效导致系统故障占的比重很大，而且其中超过50%的故障是因IGBT模块（6组IGBT及其反并联二极管构成）功率循环失效造成的[1-4]。此外，GB／T25388.1—2010《风力发电机组双馈式变流器技术条件》对风电机组适应风况的能力提出了明确要求，其中一项重要指标是变流器在各典型风况下其平均失效时间MTTF（Mean Time To Failure）不小于2 a[5]。另外，风电变流器IGBT模块结温的大小、波动幅值及波动频率与风速密切相关，因此，风速可能对IGBT模块的失效产生影响[1-2，5]。 综上所述，如何准确评估不同风况下风电变流器IGBT模块功率循环能力并分析风速对其的影响规律，以提高变流器可靠性显得十分重要。

目前，已有文献主要是基于器件结温来衡量变流器IGBT模块功率循环能力。如文献[6-7]利用评估手册MIL-HDBK-217F，分析了变流器拓扑结构对IGBT模块功率循环能力的影响；文献[8]利用电子设备评估模型，对混合电动汽车中逆变器IGBT模块的功率循环能力进行了评估。但上述评估方法仅关注结温平均值对IGBT模块功率循环能力的影响，而没有考虑结温波动的影响。文献[9-10]基于IGBT模块功率循环失效模型，分析了风速及风机参数对永磁同步风电机组网侧变流器功率循环能力的影响。但由于机侧变流器长期处于低频下运行，且运行频率随风速的变化而改变，使得机侧IGBT模块的结温波动幅值更大，且波动频率随风速随机变化，因此现有网侧评估模型很难对机侧变流器IGBT模块的结温波动信息进行准确提取。文献[11]分析了机组控制方式对机侧变流器IGBT模块功率循环能力的影响，但分析模型假设各风速区间的风速为恒定值，并未考虑各区间内风速的变化。因此，有必要研究湍流风速下机侧变流器IGBT模块功率循环能力的准确评估方法。

基于此，本文在分析结温大小及波动对机侧变流器IGBT模块失效影响的基础上，结合双馈风电机组仿真模型，基于变流器实时运行参数，建立机侧变流器IGBT模块结温计算模型，并分析湍流风速对IGBT结温波动的影响；其次，考虑湍流风速导致器件结温随机波动的特点，提出基于雨流算法提取随机结温波动信息的机侧变流器IGBT模块功率循环能力评估模型。最后，以某1.5MW双馈风电机组机侧变流器IGBT模块为例，对传统功率循环能力评估模型和本文模型的有效性进行比较，并分析年平均风速及湍流强度对机侧变流器IGBT模块功率循环能力的影响。

1 机侧变流器IGBT模块失效模型

1.1 器件功率循环失效模型

功率循环是IGBT及二极管器件在工作中失效的主要诱因，这是由器件材料的热膨胀系数不同导致的。当器件的温度波动变化时，材料形成不同程度上的压缩或拉伸从而产生剪应力，最终使器件因功率循环疲劳累积而失效[10-11]。LESIT项目利用不同器件制造商的IGBT模块，通过功率循环试验，得出器件发生失效主要与结温及其波动幅值有关，见图1[12]。

图1 Nf与 Tm及ΔTj的关系Fig.1 Relationship among Nf，Tmand ΔTj

图中，ΔTj、Tm分别为结温波动幅值及平均值。从图1可以看出，随着ΔTj或Tm的增大，器件可进行的功率循环次数减少，而且ΔTj对器件寿命的影响比Tm更为显著。基于器件失效机理，总结出器件的Coffin-Manson 失效寿命模型[12]：

其中，Nf（Tm，ΔTj）表示在 Tm及 ΔTj下器件可进行的功率循环总次数；A、α为与器件相关的常数，文中分别取值640、-5；Q为激活能量常数，取值0.8eV；R为玻尔兹曼常量。

为了预测在工作条件下器件的平均失效时间，通常采用线性疲劳累计损伤模型，由此，器件的平均失效时间 tdevice可计算如下[12]：

其中，N（Tm，ΔTj）表示在时间段 T 内，器件所经历的结温波动幅值及平均值分别为ΔTj及Tm时的功率循环次数。

1.2 机侧变流器IGBT模块的平均失效时间

为衡量器件结温对机侧变流器IGBT模块失效的影响，本节基于器件功率循环失效模型，结合双馈风电机组拓扑结构（如图2所示），建立机侧变流器IGBT模块的平均失效时间计算模型。

图2 双馈风电机组拓扑结构Fig.2 Topology of DFIG unit

由图2可知，机侧变流器IGBT模块由6组IGBT及反并联二极管组成。在由M个器件组成的系统中，系统的平均失效时间tsystem定义如下[12]：

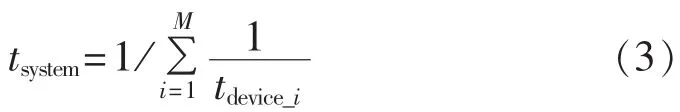
则机侧变流器IGBT模块的平均失效时间tsystem可计算如下：

其中，tdevice_I、tdevice_D分别为IGBT和二极管的平均失效时间，其可由式（2）计算。

2 湍流风速对机侧变流器结温波动的影响

2.1 机侧变流器IGBT模块结温计算模型

为准确计算机侧变流器运行过程中IGBT模块的结温，本节基于开关周期损耗计算方法及机侧变流器功率模块热模型，结合机侧变流器运行参数，建立机侧变流器结温计算模型。

对于双极性正弦脉宽调制的三相变流器，IGBT与二极管基于开关周期的导通损耗PIc与PDc分别如式（5）、（6）所示[17-19]：

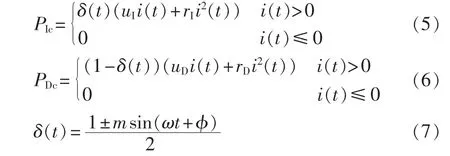
其中，uI、uD分别为 IGBT、二极管的饱和压降；rI、rD分别为IGBT、二极管的导通电阻；i（t）为变流器输出电流；δ（t）为占空比；“±”内的“+”、“-”分别用于机侧变流器逆变和整流工作模式；m为调制度；ω为角频率；φ为交流电压和电流基波分量之间的相位角。

IGBT与二极管基于开关周期的开关损耗PIs与PDs分别如式（8）、（9）所示[17-19]：

其中，fs为开关频率；Eon、Eoff分别为 IGBT 额定条件下的单位开通、关断损耗；Udc为变流器直流侧电压；UN、IN分别为IGBT额定电压和额定电流；Erec为二极管额定条件下的单位恢复损耗。

单个IGBT与二极管的总损耗PI及PD分别表示如下：

机侧变流器功率模块的总损耗Ptot为：

机侧变流器功率模块的热模型如图3所示，则IGBT的结温TIj与二极管的结温TDj分别计算如下：

图3 机侧变流器IGBT模块的热模型Fig.3 Thermal model of IGBT modules of generator-side converter

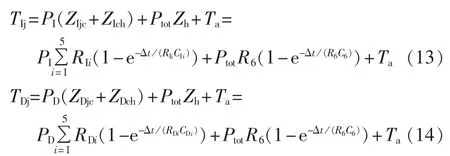
其中，ZIjc、ZDjc分别为IGBT、二极管的结-壳热阻抗，ZIch、ZDch分别为IGBT、二极管的管壳至散热器热阻抗，Zh为变流器功率模块散热器的热阻抗，上述热阻抗分别由各自的等效热阻及热容构成，其具体参数可根据厂商提供数据获取；Ta为环境温度；Δt为损耗持续作用的时间，且Δt=f／2，f为变流器运行频率。

基于上述损耗计算方法及热模型，机侧变流器IGBT模块结温计算步骤如下：首先利用厂商提供数据，可得各项损耗特性参数 uI、uD、rI、rD、Eon、Eoff、Erec、Un、In及热网络模型参数 ZIjc、ZDjc、ZIch、ZDch、Zh；然后，结合双馈风电机组仿真模型，在考虑机组控制特性的基础上，获取机侧变流器运行参数fs、Udc、m、φ、i（t）及 ω，即可得到各时刻下的损耗 PI、PD、Ptot，进而通过构建的热模型，便可获得IGBT或二极管结温。

2.2 湍流风速对结温波动的影响

为分析湍流风速对机侧变流器IGBT模块结温的影响，本文基于MATLAB平台，首先利用短期风速仿真模型[20]，构造 2 组平均风速均为 11m／s、但湍流强度分别为0%及15%的风速，以模拟恒定风速及湍流风速；然后，基于2.1节中建立的结温计算模型，以某1.5MW双馈风电机组机侧变流器IGBT为例，对比分析恒定及湍流风速下IGBT的结温特性。双馈风力发电机组的主要参数如下：额定功率为1.5 MW；额定电压为690V；直流侧电压为1150V；额定频率为50Hz；额定转速为 1800 r／min；定子电阻 Rs为 0.00706 p.u.；转子电阻 Rr为 0.005 p.u.；定子漏感 Lsl为 0.171 p.u.；转子漏感 Lrl为 0.156 p.u.；定、转子互感Lm为2.9 p.u.；同步转速点风速为9.325m／s；恒转速区起始点风速为11.3 m／s；恒功率区起始点风速为 12.3 m ／s；切出风速为 25 m ／s。

图4为恒定和湍流风速下，机侧变流器IGBT结温。 图4（a）为仿真风速；图4（b）为恒定风速下机侧变流器IGBT结温，由图可知其结温的Tm、ΔTj及波动频率均恒定，分别为 57.8℃、11.5℃及 6Hz；图 4（c）为湍流风速下IGBT结温，基于雨流算法对图中的结温数据进行统计可知，Tm的最大值为60.5℃、最小值为55.3℃，ΔTj的最大值为34.2℃、最小值为8.9℃，波动频率的最大值为12Hz、最小值为0.3Hz，由此可见，Tm、ΔTj及波动频率随时间而随机变化，尤其是ΔTj及波动频率变化较为剧烈。此外，对比图4（b）、（c）可知，湍流及恒定风速下结温的Tm相差不大，但两者结温的ΔTj及波动频率存在显著差异，尤其是湍流风速下存在具有较大ΔTj的结温，其可能对IGBT模块的平均失效时间产生较大影响。

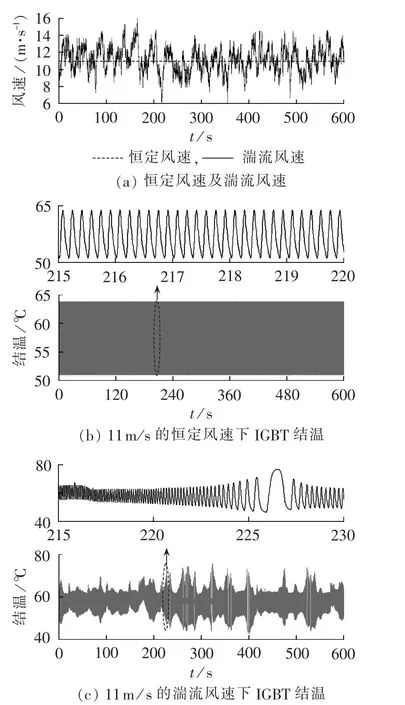
图4 恒定／湍流风速下，机侧变流器IGBT结温Fig.4 Junction temperature of generator-side converter IGBT for constant and turbulent wind speeds

3 IGBT模块功率循环能力评估模型

3.1 基于雨流算法的随机结温波动信息提取

针对湍流风速下器件结温的Tm、ΔTj及波动频率均随机变化，导致传统结温提取方法[9-11]不能有效提取其结温波动信息的问题，考虑雨流算法具有简单、直观、计算量小等特点，本文提出利用雨流算法对随机结温载荷进行提取，以准确统计一段时间内器件结温的 ΔTj、Tm及 N（Tm，ΔTj）。

雨流算法由Matsuiski和Endo等人提出，主要用于分析材料的应力-应变演化规律[21]。其用于提取器件结温波动信息时的步骤如下。

a.把结温-时间曲线旋转90°，采用竖坐标轴表示时间，横坐标轴表示结温，如图5所示。

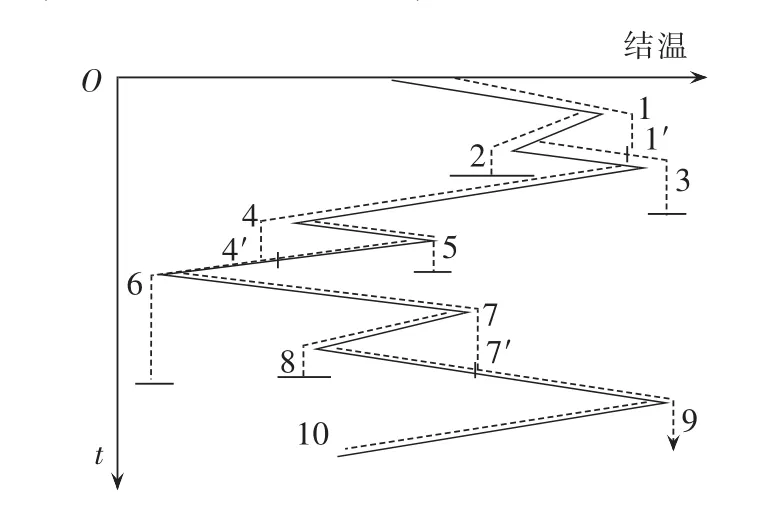
图5 基于雨流算法提取随机结温波动信息Fig.5 Random junction temperature fluctuation information extraction based on rain-flow algorithm

b.规定雨点以峰值（或谷值）为起点沿各层层顶向下流动，然后根据雨点的轨迹（图中虚线所示）提取器件结温波动信息：即雨滴从每个谷值外边（或峰值内边）开始流动，在峰值（或谷值）处竖直落下并继续流动，一直流到比起始点值更大的峰值（或更小的谷值）处停止；此外，若雨滴在流动过程中，遇到上层斜面流下的雨滴时也停止流动。当雨滴停止流动时，其轨迹就会形成一个闭合曲线，即一个完整的结温波动循环。

c.根据结温波动循环的起点值To和终点值Ts，结温的 ΔTj、Tm可分别由式（15）、（16）计算，且对应的结温波动次数 N（Tm，ΔTj）加 1。

d.重复步骤b、c，直至结温-时间历程末点。

3.2 IGBT模块功率循环能力评估模型

基于雨流算法提取随机结温波动信息，并结合风速的统计特性[22]，建立机侧变流器IGBT模块功率循环能力评估模型，其评估流程如图6所示，其评估步骤如下。

a.将 0～30m／s的风速，以 1 m／s为间隔，划分为30个风速区间，各风速区间的分布概率用fk表示，平均值用vk表示，湍流强度用Ik表示；根据年风速的统计特性[22]，将vk取为各风速区间的中间值（即0.5、1.5、…、29.5 m／s）；fk符合 Rayleigh 分布，其与年平均风速vave的关系如式（17）所示；Ik与年风速的湍流强度Iref的关系如式（18）所示。

图6 机侧变流器IGBT模块功率循环能力评估流程图Fig.6 Flowchart of MTTF assessment for IGBT modules of generator-side converter

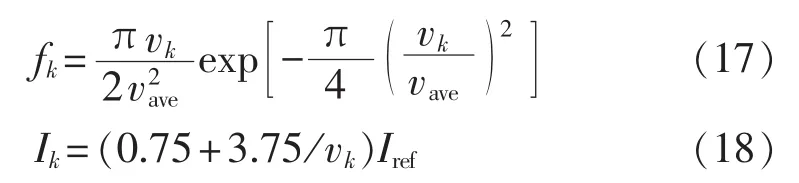
b.基于MATLAB／Simulink仿真平台，利用湍流风速仿真模型，得到各风速区间的时序风速，时序风速的持续时间为T（通常取600s），并基于风电机组仿真模型及机侧变流器结温计算模型，得出各风速区间下机侧变流器IGBT模块的结温载荷，然后利用雨流算法提取 Tm、ΔTj及 N（Tm，ΔTj），再利用式（1）—（4）计算各风速区间下机侧变流器的平均失效时间tk。

c.结合各风速区间的分布概率fk，基于Miner线性累加原则，利用式（19）便可预测各区间风速综合作用下，机侧变流器IGBT模块的平均失效时间ttot。

4 年平均风速及湍流强度对IGBT模块功率循环能力的影响

4.1 年平均风速的影响

为研究年平均风速对机侧变流器IGBT模块功率循环能力的影响，结合《风力发电机组双馈式变流器技术条件》[5]中定义的典型风况，选取不同年平均风速、相同湍流强度的4种风况（vave分别为6、7.5、8.5、10 m／s，Iref均为 0.12），基于本文建立的机侧变流器IGBT模块功率循环能力评估模型，以某1.5MW双馈风电机组机侧变流器IGBT模块为例，对其在上述4种风况下运行时，IGBT模块的平均失效时间进行计算，并将此计算结果与利用传统模型[9-11]的评估结果进行比较。机侧变流器参数为：Udc为1200 V；Ta为30℃；IGBT模块型号为FF1000R17IED_B2。其损耗参数：UN、IN分别为 1700 V 和 800A；fs为 4000Hz；uI、uD分别为 3.1、1.2 V；rI、rD分别为 3.3×10-3、2.3×10-3Ω；Eon、Eoff、Erec分别为 260、350、120 mJ。 热网络参数如下：RI1—RI5分别为 0.8、3.7、13、2.5、16 K ／kW；RD1— RD5分别为 2.19、8.41、21.94、2.56、16K ／kW；R6为 5 K ／kW；CI1—CI5分别为 1、0.3514、3.8462、240、6.25 s·W／K；CD1—CD5分别为 0.365、1.55、2.27、234、7.13 s·W／K；C6为 166.7 s·W／K。

表1显示了不同年平均风速、相同湍流强度下，本文模型及传统模型的评估结果。由表1中本文模型的评估结果可知，随着年平均风速从6 m／s增大到10 m／s，机侧变流器IGBT模块的平均失效时间从1.56 a减小到0.93 a。同时，表中传统模型评估结果也表明，IGBT模块的平均失效时间随着年平均风速的增大而减小，此变化规律与本文模型评估结果的变化规律相同，验证了本文模型的有效性。另外，对比表中相同年平均风速下不同模型的评估结果可知，本文模型的评估结果小于传统模型的评估结果，可见传统评估模型的结果偏乐观。这是由于本文模型同时考虑了风速平均分量和风速湍流分量，而传统模型仅考虑各风速区间内风速平均分量。此外，由表1还可知：各典型风况下机侧变流器IGBT模块平均失效时间均小于2 a，无法满足《风力发电机组双馈式变流器技术条件》[5]中的要求。

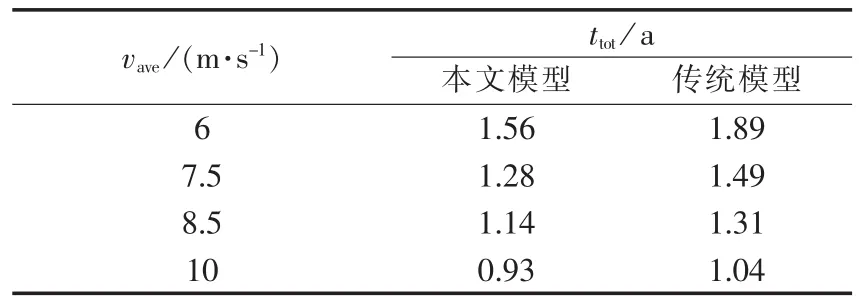
表1 不同年平均风速下不同模型的评估结果Table 1 Assessment result by different assessment models for different annual average wind speeds

4.2 湍流强度的影响

为分析风速湍流强度对机侧变流器IGBT模块功率循环能力的影响，结合变流器典型运行风况[5]，选取年平均风速均为6m／s，但湍流强度Iref分别为0.12、0.14、0.16的3种风况，基于本文建立的IGBT模块功率循环能力评估模型，对机组在上述风况下运行时，其机侧变流器IGBT模块的平均失效时间进行计算，计算结果如表2所示。

表2 湍流强度不同时机侧变流器IGBT模块的平均失效时间Table 2 MTTF of generator-side converter IGBT module for different turbulence intensities

由表2可知，当湍流强度取最小值0.12时，机侧变流器IGBT模块的平均失效时间最大，为1.56 a；而当湍流强度取最大值0.16时，机侧变流器IGBT模块的平均失效时间最小，为1.29 a。由此可知，机侧变流器IGBT模块的平均失效时间随湍流强度的增大而减小。

5 结论

本文在分析结温平均值及波动幅值对机侧变流器IGBT模块失效影响的基础上，结合双馈风电机组仿真模型，基于变流器实时运行参数，建立机侧变流器IGBT模块结温计算模型，分析湍流风速对结温波动的影响，进而提出基于雨流算法提取随机结温波动信息的机侧变流器IGBT模块功率循环能力评估模型，并以某1.5MW双馈风电机组机侧变流器IGBT模块为例，分析年平均风速及湍流强度对其功率循环能力的影响。所得结论主要如下。

a.与恒定风速下机侧变流器IGBT结温相比，湍流风速作用下结温的平均值、波动幅值及波动频率不再保持恒定，而呈现随机变化的特性；且相比于结温的平均值，结温波动频率及波动幅值的大小受湍流风速的影响较大。

b.与仅考虑各风速区间风速恒定分量作用的传统评估模型相比，本文提出的基于雨流算法提取随机结温波动信息的评估模型能同时考虑风速的恒定分量及湍流分量的作用，更能准确反映湍流风速对机侧变流器IGBT模块功率循环能力的影响。

c.随着年平均风速及湍流强度的增大，机侧变流器IGBT模块的平均失效时间减小，功率循环能力减弱。

本文实现了湍流风速作用下变流器IGBT模块可靠性的定量分析；本文模型及结论为不同风况下风电场选择合适的IGBT模块，以提高其运行可靠性、降低运行及维护成本，提供了重要的理论依据。