不平衡工况下链式STATCOM的运行极限分析

谭树龙，杨 耕，耿 华

（清华大学 自动化系，北京 100084）

0 引言

静止同步补偿器（STATCOM）作为一种并联无功补偿装置被广泛应用于现代电力系统[1]。在高压大功率的应用场合，链式结构的STATCOM近年来逐渐成为研究的热点[2-3]。它有三角形和星形2种主要结构。

链式STATCOM（以下简称STATCOM）各个链节直流电压基本恒定是装置安全可靠运行的前提[4]。在并网电压，即公共连接点（PCC）的电压不平衡或补偿无功电流不平衡的工况下，STATCOM的各相支路将持续输入或输出一定的有功功率[5]。这会导致支路中的链节直流电压不稳定，影响装置的可靠运行。针对这一问题，目前有一些文献提出了不同的控制方法[5-10]。这些方法虽然表现形式各有差异，但是其最终效果都是在三角形STATCOM各相支路叠加零序电流、星形STATCOM各相支路叠加零序电压，通过零序分量的作用实现STATCOM各相支路的有功功率为零。也有文献提出基于负序分量的控制方法[11-12]，但适用场合受到较大的局限[13]。 因此本文只讨论基于零序分量叠加的控制方法。

基于零序分量叠加的控制方法增大了STATCOM各相支路流过的电流或支路承受的端电压[10]。因此在装置额定电流或额定电压一定时，STACTOM能够可靠运行的不平衡工况范围是有限的。截至目前，绝大多数文献侧重于控制方法的研究。只有极少数的文献对星形STATCOM在补偿无功电流不平衡工况下的运行极限进行了量化分析[10，13]。 然而，目前已有的文献对三角形STATCOM受额定电流约束的运行极限鲜有报道；对并网电压不平衡条件下的运行极限也未见详细的分析。本文将在已有文献的基础上进一步完善这部分工作。

本文首先分析在不平衡工况下影响STATCOM额定电流和额定电压的关键因素，定量给出在三角形STATCOM额定电流与星形STATCOM额定电压一定的条件下，装置能可靠运行的不平衡工况范围及其分析方法。在此基础上，对三角形STATCOM和星形STATCOM在不平衡工况下的运行极限进行比较。最后通过仿真实验对运行极限分析的结果进行验证。

1 零序分量

三角形STATCOM的并网系统结构如图1所示。

所有不平衡工况对STATCOM而言表现为2个方面的特征：并网电压不平衡与补偿无功电流不平衡。在此，同时考虑这2个方面的不平衡特征，以三角形STATCOM为例，给出了统一的零序分量计算方法，并进一步研究了影响零序分量的关键因素。

1.1 基于零序分量叠加的控制原理

在STATCOM并网电压（即PCC电压）不平衡的情况下，三角形STATCOM各相支路的电压为：

其中，Up、Un分别为电压正、负序分量的幅值；θpu、θnu分别为正、负序电压相位。

考虑叠加的零序电流分量，三角形STATCOM各相支路流过的电流如式（2）所示：

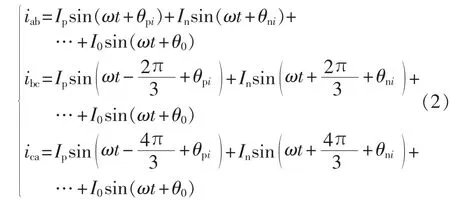
图1 三角形STATCOM并网系统结构图Fig.1 System configuration of delta-connected cascaded STATCOM

其中，Ip、In分别为补偿无功电流正、负序分量的幅值；θpi、θni分别为正、负序电流相位。

根据式（1）和式（2）可导出各相支路的有功功率：

三角形STATCOM的三相支路有功功率总和为：

作为并联无功补偿设备，STATCOM补偿的正、负序电流均为无功电流，即：

因此三相支路总的有功功率为零，即有：

为了维持各支路中链节的直流电压基本恒定，需要在三角形STATCOM中叠加零序电流，以保证各相支路输入或输出的有功功率为零。由于已有式（9）的约束，叠加的零序电流只需满足式（10）即可：

将式（10）代入式（3）、式（4），并经过一系列推导得：

方程组（11）的解可表示为：

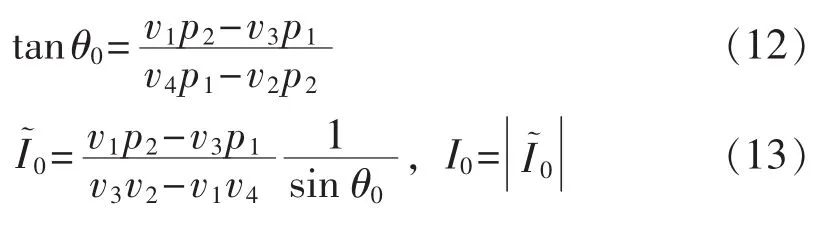
图2 零序电流的作用机理Fig.2 Functional mechanism of zero-sequence current

如图2所示，在一定的并网电压不平衡度与补偿电流不平衡度条件下，三角形STATCOM各相支路的电流原本与相应的端电压并不垂直，例如相量Ibc0与Ubc之间的夹角不为90°，bc支路存在有功功率变化。叠加适当的零序电流I0之后，各相支路的电流垂直于相应的端电压。对于星形STATCOM，可类似推导其在不平衡工况下所需叠加的零序电压表达式。基于零序电压叠加的控制方法，可实现星形STATCOM在不平衡工况下的可靠运行。

1.2 零序分量的影响因素

由式（12）、（13）可知，三角形 STATCOM 在不平衡工况下所需叠加的零序电流受 Up、Un、Ip、In、θpu、θnu、θpi、θni等因素影响。为便于对零序分量进行定量研究，必须进一步分析其中的关键影响因素。在实际控制中通常取正序电压相位为参考，即：

将式（15）代入式（12）与式（13），经过一系列推导得：

其中，DU与DI分别为电压不平衡度与电流不平衡度。

STATCOM作为并联无功补偿设备，补偿的正、负序电流均为无功电流。因此有：

将式（18）代入式（16）、（17），发现正、负序电流的容性与感性特征对零序电流具有重要影响。通过改进电流不平衡度的定义可以简化表达这种影响。为此，改进电流不平衡度的定义为：

将式（19）代入式（16）、（17）可得：

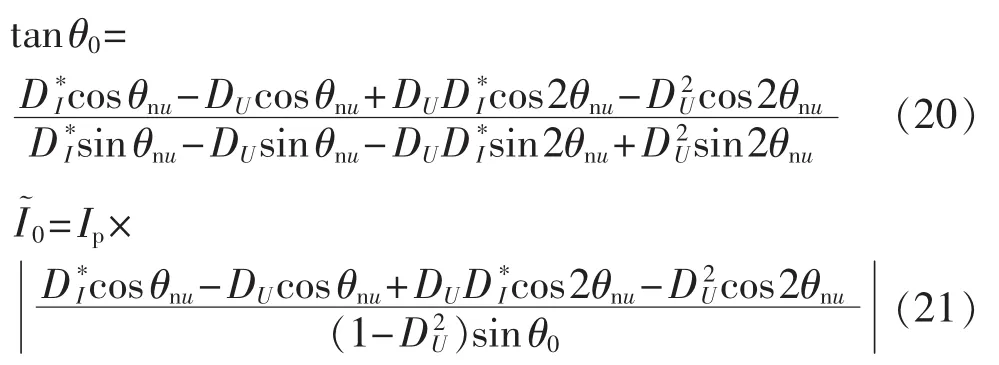
通过式（20）、（21）可以发现，三角形 STATCOM在不平衡工况下所需叠加的零序电流仅由4个因素决定。除正序无功电流的幅值Ip之外，其他3个影响因素分别为：并网电压的不平衡度DU、补偿无功电流的不平衡度D*I以及并网电压中负序电压分量与正序电压分量的相位差θnu（因取定θpu=0而将二者相位差θnu-θpu简化表达为θnu）。零序电流相量满足式（22）：

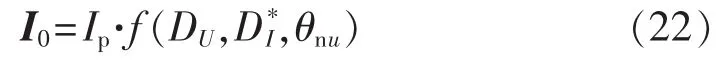
经过分析，发现对于星形STATCOM在不平衡工况下所需叠加的零序电压也有类似的结论。

2 不平衡工况范围

以三角形STATCOM为例，叠加零序电流以后，各支路的电流如式（23）所示：

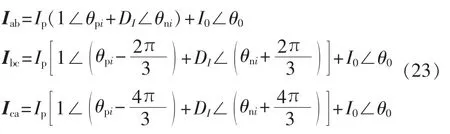
三角形STATCOM的额定电流应该取三者的最大值：

将式（15）、（18）代入式（23），再结合式（22）所示的函数关系，可推导STATCOM额定电流大小与不平衡工况之间的函数关系，如式（25）所示：

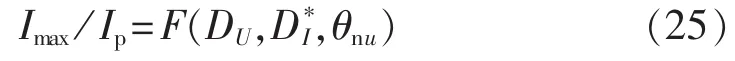
其中，DU、D*I、θnu这 3 个参数反映了 STATCOM 的不平衡工况特征；Imax／Ip反映了在此不平衡工况下，三角形STATCOM为保证可靠运行所需要的额定电流大小。通过分析发现，当DU与D*I2个参数取定之后，Imax／Ip随θnu的变化呈现周期性变化规律，如图3中实线所示。取其峰值作为此时的Imax／Ip，可进一步将式（25）所示的函数关系简化表达为：

对于星形STATCOM而言，可类似地推导其额定电压大小与不平衡工况之间的函数关系：

其中，Umax／Up反映了在DU、D*I所决定的不平衡工况下，星形STATCOM为保证可靠运行所需要的额定电压大小。

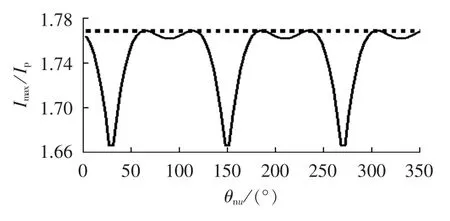
图3 Imax／Ip随θnu周期性变化的曲线Fig.3 Periodic variation of Imax／Ipalong with θnu

根据式（26）所示的函数关系，通过数值分析方法可得到三角形STATCOM的额定电流水平Imax／Ip与并网电压不平衡度DU以及补偿无功电流不平衡度D*I之间的量化关系，如图4所示。图5则表示了星形STATCOM的额定电压水平Umax／Up与不平衡工况之间的定量关系。

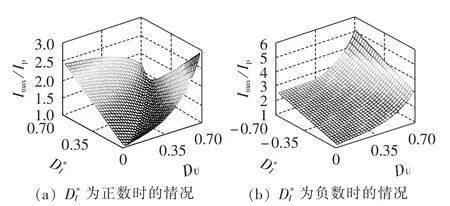
图4 三角形STATCOM额定电流的变化情况Fig.4 Variation of rated current of delta-connected STATCOM

观察图4可以发现，在三角形STATCOM的额定电流水平Imax／Ip一定的情况下，沿Imax／Ip值作一个平行于DU轴与D*I轴的平面，只有位于该平面以下的不平衡工况范围是装置能够可靠运行的区域。从控制的角度而言，当装置额定电流与并网电压不平衡度一定的情况下，为了保障装置安全可靠运行，需要根据图4的分析结果，控制STATCOM补偿无功电流的不平衡度在一定的范围内。

对比图4和图5可以发现，为保证装置在不平衡工况下可靠运行，三角形STATCOM所需的额定电流与星形STATCOM所需的额定电压同时受到DU与D*I的影响。2种STATCOM受DU与D*I的影响是对偶等效的，在DU较大的不平衡工况下，三角形STATCOM所需的额定电流显著提高；在D*I较大的不平衡工况下，星形STATCOM所需的额定电压显著提高。因此，从经济性的角度考虑，三角形STATCOM更适用于补偿无功电流不平衡度D*I较高的场合；星形STATCOM更适用于并网电压不平衡度DU较高的场合。所以有必要根据应用场合的不同适当选择三角形STATCOM或星形STATCOM。

3 仿真验证

本节以±50 Mvar／10 kV的链式STATCOM为例，通过MATLAB对上述的分析结果进行验证。需要说明的是，由于本文旨在从理论上分析链式STATCOM在不平衡工况下的可靠运行范围，而并不是提出一种实际应用的新型控制方法，因此仅通过仿真验证理论分析的正确性。仿真中涉及三角形与星形2种STATCOM，参数列于表1。需要说明的是，虽然实际中STATCOM向电网补偿无功电流会使并网电压（PCC电压）发生变化，但是由于本文的核心是说明STATCOM在一定的并网电压不平衡和补偿无功电流不平衡的情况下，三角形STATCOM的额定电流与星形STATCOM的额定电压大小，因此为了便于说明问题，在仿真中设定PCC处电压恒定。此外，本仿真的目的是验证理论分析的结果，所以忽略了PWM等环节。

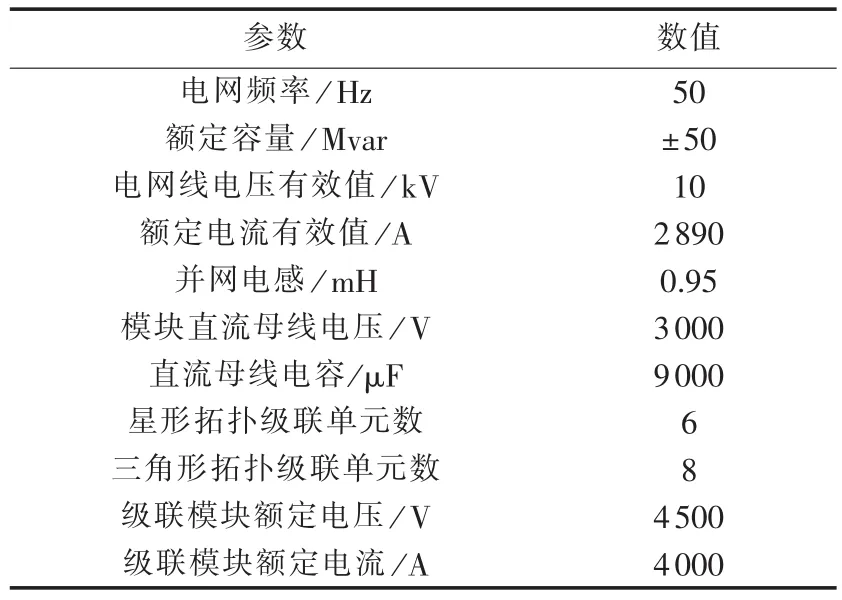
表1 STATCOM系统仿真参数Table1 Simulation parameters of STATCOM system

3.1 平衡电压条件下的STATCOM运行

STATCOM的并网电压平衡，即DU=0。此时设置电流不平衡度D*I=0.4，以三角形STATCOM为例进行仿真实验。根据图3所示的分析方法可知在这种不平衡度条件下，θnu=60°时Imax／Ip最大。本仿真以这种最严峻的情况为例，设定θnu=60°。根据图4的分析结果可知，为保障装置在这种不平衡工况下可靠运行，其额定电流幅值至少应该设计为1.8 Ip，即1.04 p.u.。 仿真结果如图 6 所示。 图 6（a）中 Ip、In分别为STATCOM向PCC补偿电流的正、负序分量标幺值，其中负序分量占正序分量的40%，对应的电流波形（标幺值）如图 6（b）所示。 图 6（c）表示 STACTOM 并网电压的正、负序分量标幺值，对应的电压波形（标幺值）如图 6（d）所示。 图 6（e）表示三角形 STATCOM内各相支路上流过的电流标幺值，其中ica幅值较大，达到1.05 p.u.，与理论分析的结果1.04 p.u.基本吻合。STATCOM各个支路中除了正、负序电流之外，额外叠加了零序电流i0，如图6（f）所示（标幺值）。零序电流叠加使得三角形STATCOM各个支路流过的电流与相应的端电压相位垂直，见图6（d）与图6（e）。最终的目的是保持各个级联模块的直流母线电压能够维持在3 kV左右，见图6（g）。为方便观察波形的细节，对图6的部分波形作了时间轴放大处理。

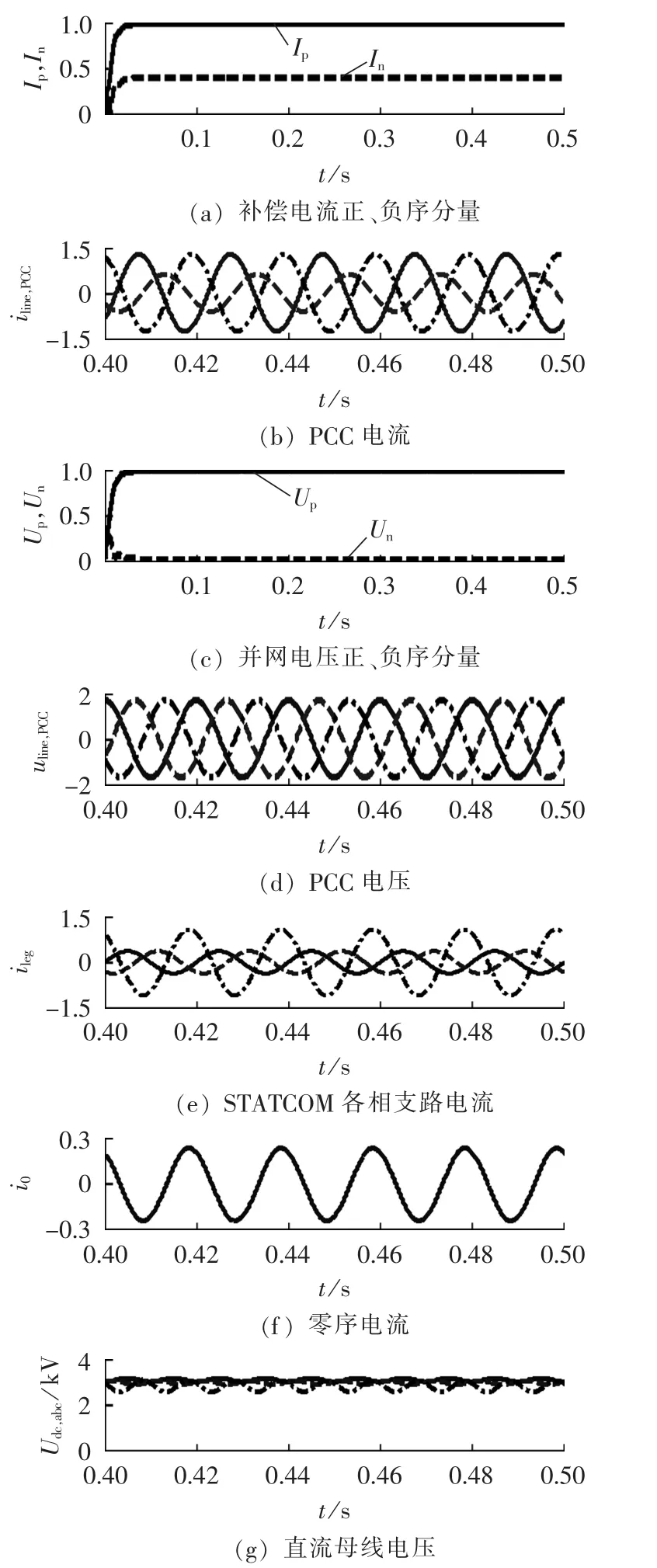
图6 三角形拓扑在DU=0、D*I=0.4下的仿真结果Fig.6 Simulative results of delta structure，when DU=0，D*I=0.4

3.2 不平衡电压条件下的STATCOM运行

本仿真设定三角形STATCOM的并网电压不平衡度DU=0.3，STATCOM向电网补偿1 p.u.的感性正序无功电流和0.4 p.u.的容性负序无功电流，即D*I=-0.4。根据图4的分析结果，三角形STATCOM的额定电流应设计为1.94 Ip，即1.12 p.u.。仿真结果如图7 所示（θnu=40°）。 图 7（e）所示三角形 STATCOM 各相支路上流过的电流波形中，ica幅值较大，达到1.14 p.u.，与额定电流幅值的理论分析结果1.12 Ip基本吻合。

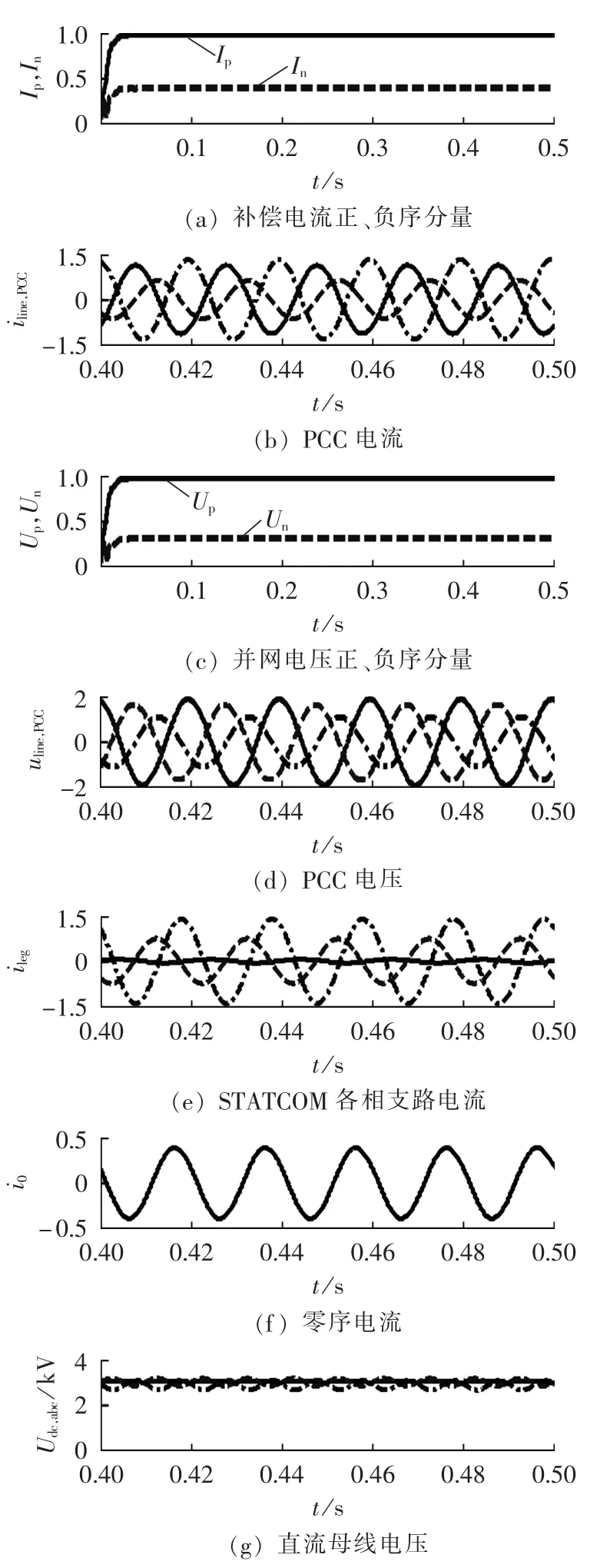
图7 三角形拓扑在DU=0.3、D*I=-0.4下的仿真结果Fig.7 Simulative results of delta structure，when DU=0.3，D*I=-0.4

为说明星形STATCOM与三角形STATCOM的对偶等效特征，对±50 Mvar／10 kV的星形STATCOM系统进行了仿真。与三角形STATCOM的不平衡工况对偶，设定DU=0.4，D*I=-0.3。理论上星形STATCOM所需的额定电压幅值应设计为1.94 Up。仿真结果如图 8 所示（θnu=18°）。 图 8（a）所示 STACTOM补偿无功电流的正、负序分量中，负序分量为0.3 p.u.，图8（c）所示STATCOM并网电压的正、负序分量中，负序分量为0.4 p.u.。图8（e）所示星形STATCOM各相支路的端电压波形中，uab幅值较大，达到1.96 p.u.，与理论分析的额定电压幅值大小吻合。

图8 星形拓扑在DU=0.4、D*I=-0.3下的仿真结果Fig.8 Simulative results of star structure，when DU=0.4，D*I=-0.3

4 结论

本文综合考虑并网电压不平衡与补偿无功电流不平衡的情况，通过对并联型链式STATCOM额定电流、电压的影响因素分析，定量给出了三角形接线STATCOM与星形接线STATCOM装置的不平衡运行能力和范围。分析可知，从优化角度出发，可根据本文给出的极限控制STATCOM输出的无功补偿电流；从经济性出发，三角形STATCOM更适用于补偿无功电流不平衡度较高的场合，而星形STATCOM更适用于并网电压不平衡度较高的场合。本文的分析方法和分析结果可应用于链式STATCOM的系统设计和控制。