基于气泡数密度模型的气体穿越液池过程气泡特性数值模拟

吴 晅，焦晶晶，王丽芳，金 光

1.内蒙古科技大学内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室，内蒙古 包头 014010；2.内蒙古科技大学能源与环境学院，内蒙古 包头 014010

基于气泡数密度模型的气体穿越液池过程气泡特性数值模拟

吴 晅1，2，焦晶晶2，王丽芳2，金 光2

1.内蒙古科技大学内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室，内蒙古 包头 014010；2.内蒙古科技大学能源与环境学院，内蒙古 包头 014010

采用考虑了气泡破碎和聚并的平均气泡数密度（ABND）输运方程，并与计算流体力学（CFD）中的湍流双流体模型相结合，建立CFD-ABND耦合计算模型。运用该模型对含固体颗粒气体通过冷却管穿越液池过程中液池内的气泡尺寸和气液界面浓度进行数值模拟。定量获得了液池内气泡尺寸和气液界面浓度分布，并分析了气速变化对其影响规律。结果表明：所建立的CFD-ABND模型能够对液池中的气泡尺寸及气液界面浓度分布等气泡特性进行较好预测；在靠近冷却管外壁面附近区域形成较大尺寸气泡和较高气液界面浓度；液池内隔板的存在有助于气液扰动，使液池内总体的气泡尺寸得到有效降低及气液界面浓度得到提升。

气化炉 洗涤冷却室 气泡尺寸 界面浓度 数值模拟

含固体颗粒气体穿越液池完成气固分离的洗涤净化过程在工业、环保和医疗卫生等领域有广泛的应用前景［1］。以煤化工领域为例，新型水煤浆气化炉洗涤冷却室主要由冷却环、冷却管和液池等部分组成［2］。从气化室出来的高温合成气进入洗涤冷却室，在室内冷却并除渣。合成气与激冷水间的传热传质过程主要发生在冷却管［3］。经激冷的合成气沿冷却管流出并进入液池，合成气得到初步净化和进一步的增湿冷却，以满足后续工艺的需要。在该过程中，存在着气液固三相共存的多相流动形式，相间流动极为复杂，各种因素相互穿插影响。前期研究［4］表明，该过程中的气液流动特征对气固分离有着重要影响，气泡特性是其中重要因素之一。王亦飞等［5-8］对气化炉洗涤冷却室内气体穿越液池过程进行了大量研究；龚晓波等［9］运用颗粒群和涡扩散理论，建立应力代数模型对原德士古气化炉激冷室内气体穿越液池过程气液流动进行了模拟，但该模型中假设液池内气泡尺寸均一，忽略了气泡的聚并和破碎行为。谢海燕等［10］运用VOF（Volume of Fluid）模型对原德士古气化炉激冷室内合成气穿越液池过程的气液流动特性及带水问题进行了模拟，但其无法对气泡大小给出定量的描述。实际上，气泡尺寸是气液流动特性的重要参数之一。在群体数平衡理论基础上建立起来的 MUSIG（Multiple Size Group）模型［11-14］考虑了气泡的破碎和聚合，能较好地获得气泡尺寸的分布规律。但该模型需要通过对每一组气泡建立相应的附加方程来求解气泡尺寸和气泡数量的变化，需要更多的计算时间并占用更多的资源，因此在一定程度上限制了其在工程领域的应用［15，16］。而基于气泡数平衡模型（Bubble Population Balance Model，简称 BPBM），采用数密度函数法建立起来的平均气泡数密度（Average Bubble Number Density，简称ABND）输运方程将气泡的分布用一个平均变量（如气泡数密度或界面浓度）来描述［17］。因此，ABND模型只需对一个方程进行求解，为一种较理想的计算手段［16］。为此，本工作将计算流体力学中的双流体多相流模型（CFD）和气泡数密度输运方程相结合，建立CFD-ABND数学模型，实现两组模型的耦合求解。对气体穿越液池过程中液池内气泡尺寸及其分布进行数值模拟。模型中考虑了气泡的聚并和破碎行为，并将模拟结果与文献中的实验数据进行了对比分析。

1 物理模型的建立

为了便于验证所建数学模型的正确性，本工作依据文献［5-8］中所搭建的洗涤冷却室冷模实验装置建立物理模型。洗涤冷却室的实验装置由有机玻璃制成，实验中采用空气和水来代替工业装置中洗涤冷却室内的气液两相流系统。采用与实验一致的构件组合方式。数值实验中参照选取文献［5］在其洗涤冷却室冷模实验中所选用的格栅式内部构件。冷却室半径（R）为0.24 m，冷却管半径（R′）为0.075 m。构件平均孔径设为0.05 m，空隙率约为0.65。每层隔板之间的距离（Δh）为0.1 m，液池静态液位（H）为0.75 m。对洗涤冷却室内与本工作研究内容无关的其它结构部分作了简化，得到如图1所示的二维轴对称物理模型。

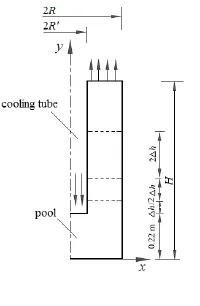
图1　物理模型示意Fig.1 Physical model of simulation

2 数学模型的构建

2.1 湍流双流体模型

在冷态的洗涤冷却室液池内，分别对气液两相流动中的每一相建立数学模型：

第q相质量守恒方程为：

第q相动量守恒方程为：

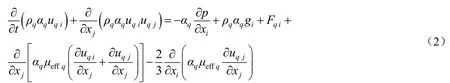
气液两相相含率满足以下公式：

式中：α为气液两相含率；ρ为密度，kg/m3；ui和uj分别为i和j方向上的平均速率，m/s；g为重力加速度，m/s2；μeff q为第q相的有效粘度，μeff= μ+μt；μt为湍流粘度（μt=Cμρk2/ε，其中，Cμ为经验常数，其值约等于0.085；k为湍流脉动动能，m2/s2；ε为湍流耗散率）；Fq i为相间作用力源项。下标g，l分别表示气相和液相。

数值模拟过程中，应用重整化群理论（Renormalization Group Theory，RNG）建立RNG k-ε湍流模型分别对每一相求解湍流方程来描述两相湍流。

式中：Gk表示由于平均速率梯度引起的湍动能产生项；C1 ε，C2 ε为常数，分别为 1.42，1.68；

相间动量交换相可以表示为：

式中：db为气泡Sauter平均直径，m；u为速率，m/s；CD为相间曳力系数。CD表达式与流型有关，计算如下：

当气泡在液体中快速上升时，液相流场必然存在较大的速度梯度，使得在速度梯度方向气泡两侧压力不同，从而对气泡产生垂直于气泡与液相流场相对速度方向的升力。气泡的升力应用下式计算［19］：

式中，CL为 升力系数。根据Drew等［20］的研究，有：

式中，CL 0为0.5，［ ］表示取最小值。

当气泡在流体中做加速运动时，其周围的部分液体被加速。由于液体有惯性，表现为对气泡有一个反作用力。这时，推动气泡运动的力将大于气泡本身的惯性力，就好像气泡质量增加一样。这部分大于气泡本身惯性力的力叫做虚拟质量力（附加质量力）。气泡所受到虚拟质量力由下式表示［18］：

式中，CVM为虚拟质量力系数，其对应于被加速液体的体积与气泡体积之比。在不同工况条件下，虚拟质量力系数的选取有一定差别。在本工作中，根据Buwa等［21］的推荐，取CVM为0.5。

2.2 气泡数密度输运方程

基于气泡数平衡模型，运用数密度函数法建立平均气泡数密度输运方程［16］：

式中，n为气泡数密度，m-3；coφ 和brφ分别表示由于气泡聚并和破碎所产生的源项。n描述了气泡数目在属性空间、位置空间以及时间空间上的分布；假设气泡尺寸由气泡Sauter平均直径来描述。

气泡数密度可定义为：

将式（14）代入式（12）即可得与Wu等［22］相一致的气液界面浓度输运方程：

其中，Aif为界面浓度（Interfacial Area Concentration，简称IAC），即单位混合物容积中包含的相界面面积，其是描述气液两相流内部几何结构的重要参数，表征了相间发生质量、动量和能量传输的有效面积大小［23，24］。可见，气泡数密度输运方程与气液界面浓度输运方程两者是相互关联的。这样就可以通过局部气含率和气泡尺寸进一步求得局部气液界面浓度。

气泡数密度输运方程中的气泡聚并和破碎行为采用Yao等［25］模型来描述。在气液体系中，由于气泡的摆动以及液相的湍动，使得气泡具有一定的湍动速率，气泡之间由于瞬时的运动速率不同而相互发生碰撞，其中，碰撞的气泡一部分会发生聚并。气泡聚并模型如下［25］：

式中，根据Yao等［25］的研究，取最大允许空隙率（αmax）为0.52。Weber数（We）表征湍流剪切力与表面张力比值：

式中，临界Weber数（Wecr）为1.24，系数Cco 1，Cco 2和Cco 3分别为2.860，1.017和1.922。

描述气泡破碎过程，需要同时给定气泡破碎速率和气泡大小分布。气泡破碎机制包括湍流涡体碰撞、液体流场剪切以及大气泡表面不稳定等几种。但在一般气液两相体系中与湍流涡体碰撞所引起的气泡破碎为主要机制。因此，气泡破碎模型如下式［25］：

式中，系数Cbr 1为1.6，Cbr 2为0.42，临界Weber数的取值同上。

2.3 求解条件及计算方法

考虑到FLUENT软件中没有ABND模型，为此采用该软件作为计算平台，对其进行二次开发。编制用户程序完成相间作用力模型、气泡数密度输运方程、气泡聚合、破碎模型以及气泡尺寸和气液界面浓度的计算。从而实现双流体模型与气泡尺寸计算模型的耦合求解。固体壁面设为无滑移无渗透壁面。对近壁面的网格采用壁面函数法处理。在液池液面上添加一小段气相区域，以确保液体不从液池中溢出，而只让气体溢出（即αl为0，αg为1）。承接冷却管内的气液两相流动，设定入口αg为0.98［7］。气液具有相同的入口速度。出口为压力出口，压力设定为一个标准大气压。压力与速度的耦合采用压力耦合方程组的半隐式方法（Semi-Implicit Method for Pressure Linked Equations，SIMPLE）进行相间耦合计算，动量方程、湍动能方程及湍动能耗散方程离散格式采用二阶迎风格式，体积分数方程采用对流项的二次迎风插值（QUICK）格式进行离散。气泡数密度输运方程的离散格式采用一阶迎风格式。采用均匀分布的结构化网格体系，水平方向上共布置60个网格。在高度方向共布置了135个网格。其中，所划分网格的无关性分析详见参考文献［4］。将湍流双流体模型与平均气泡数密度方程进行耦合求解。计算步骤为：（1）根据设定的气泡分布初始值计算相间作用力模型；（2）求解湍流双流体模型，计算得到洗涤冷却室液池内气液两相的速度场、气含率、湍动能以及湍流耗散率；（3）将以上计算得到的变量值代入气泡数密度输运方程，并进行求解，计算得到新的气泡尺寸分布和气液界面浓度分布；（4）依据计算得到的新的气泡尺寸对气液两相间的相互作用力和湍流模型进行修正；（5）运用改进后的欧拉双流体模型，重新从步骤（2）开始，以此循环，直到计算结束。

3 结果与讨论

图2给出了液池静态液面高度为0.75 m，液池内表观气速为0.5 m/s，不同时刻洗涤冷却室液池内的气含率、液体流函数等值线以及气泡Sauter直径分布的数值模拟结果。

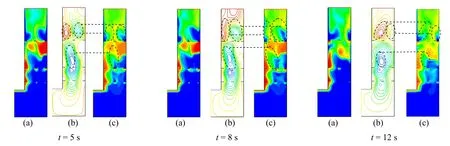
图2　气体穿越液池过程液池内不同时刻的数值计算结果Fig.2 Simulation results in pool in process of gas-solid flow passing through pool at different time

液池内分隔板的存在对大气泡具有一定的破碎作用。分隔板能够将原先直径大于11 mm的气泡破碎成小于6 mm左右的气泡或更小的气泡。另外，分隔板的存在促进了气液两相之间的扰动，使得液体在各层隔板间产生回流。气液回流增强了气液间的湍流强度。如图中虚线所标示的，涡旋的存在加剧了气泡的破碎程度，使气泡直径变小，并产生小于5 mm的小气泡。同时还可以看到，在隔板的下方，尤其是在靠近洗涤冷却室外壁面附近，由于受到隔板的阻挡，该处的气液速率小，气泡在此处停滞并逐渐聚集。此时气泡的聚并起主导作用，使得该处的气泡尺寸增大。同样，在离开最上层隔板后，破碎的气泡在上升到液面的过程中，部分气泡产生聚并使得局部的气泡直径变大。此外，气体从冷却管出口进入液池后反折，沿着冷却管外壁向上流动，因此直径为9 mm以上的气泡出现在冷却管外壁面附近。但随着各层分隔板的破碎和扰动作用，大气泡被破碎成小气泡，从而促进了气泡在液池内的扩散。

图3　局部平均气泡直径沿径向分布Fig.3 Radial distribution of local average diameter of bubble

当液池静态液面高度为0.75 m，液池内表观气速为0.5 m/s，测量高度（y）为0.34 m处测得局部平均气泡直径（db）沿径向的变化规律，结果如图3所示。图中，r为冷却室径向坐标值，对径向坐标作无量纲处理（r/R′）。从图中可知，沿径向方向，液池内平均气泡直径逐渐变小。大气泡主要集中在靠近冷却管外壁面附近。这是与气含率的分布相关的，气体主要在冷却管外壁面附近聚集，此处的气含率较高，这使得该区域内气泡之间碰撞聚并产生大气泡的概率上升，因而该区域的平均气泡直径增大。在靠近洗涤冷却室外壁面附近，气泡直径较小。在r/R′小于2.0的区域，气泡直径的变化较为显著，而在大于2.0的区域，气泡直径变化较为平缓，分布较为均匀。此外，图中显示了模拟计算结果与实验结果的对比，可见两者吻合较好，这表明所建立的模型能够适用于对洗涤冷却室内的气泡分布特性进行分析研究。

图4显示了液池静态液面高度为0.75 m，测量高度为0.44 m，径向r/R′为2.0处，计算得到的局部平均气含率、局部平均气泡直径以及局部平均气液界面浓度随液池内表观气速的变化规律。随着表观气速的增加，气含率增大，并且其增加幅度逐渐趋于平缓，说明液池中的气体含量已接近饱和。平均气泡直径呈逐渐增大的趋势。但气速增加到0.6 m/s后，气泡直径随气速变化趋于平缓。因为在液池内，随着表观气速的增加，气泡的运动程度更加剧烈，气泡与气泡之间碰撞聚并的几率提高，从而使得气泡直径增大。但同时气液间的扰动随着表观气速的增加而增强，所产生的涡旋又促进了气泡的破碎。所以随着表观气速的增加，平均气泡直径呈现增加后逐渐趋于平缓的变化趋势。随着表观气速的增加，液池内局部平均气液界面浓度增大。这是由于气速的增加，增强了气液之间的扰动，气液掺混加强，从而提高了气液界面浓度。但从图中可以看到，当气液界面浓度增大到一定值时，气液界面浓度增大的趋势变缓，说明此时气泡在液池内的扩散已接近平衡达到饱和。从图中可见，三者的变化趋势一致。

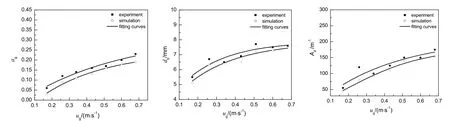
图4 αg，db及Aif随表观气速的变化Fig.4 Effect of superficial velocity on αg，dband Aif

图5给出了液池内气液界面浓度沿径向变化的规律。其计算条件是，液池静态液面高度为0.75 m，液池内表观气速为0.5 m/s，测量高度为0.44 m。理论计算与实验结果均表明，沿着液池的半径方向，气液界面浓度呈逐渐减少的变化趋势。界面浓度的峰值出现在靠近冷却管外壁面附近。随后界面浓度沿径向逐渐降低并趋于稳定。气相主要聚集在冷却管外壁面附近。气液界面浓度表征了气液两相间发生质量、动量和能量传输的有效面积大小。气液界面浓度增大，也就是气液两相间发生质量、动量传递的有效面积就越大，这就使得气液间扰动越为激烈。由于冷却管外壁面附近区域是气液扰动较为活跃的区域，其反过来也验证了气液界面浓度峰值出现在该区域的分布特性。此外，将界面浓度分布的数值模拟结果与实验结果对比可见，总体上，两者变化趋势一致，说明所建立模型可以对气液界面浓度分布进行分析计算。

图5　局部平均气液界面浓度沿径向分布Fig.5 Radial distribution of local average gas-liquid IAC

4 结 论

建立了考虑气泡破碎和聚并行为的CFD-ABND耦合计算模型，数值模拟研究了气体穿越液池过程中气泡尺寸分布及气液界面浓度分布规律：

a）模拟结果与实验结果吻合较好，证明所建立的CFD-ABND模型能够用于气体穿越液池过程中液池内气泡尺寸及气液界面浓度分布的数值预测。

b）随着液池内表观气速的增加，液池内局部气含率、气泡直径以及气液界面浓度呈增大趋势，并逐渐趋于平缓，三者的变化趋势一致。

c）液池内，在靠近冷却管外壁面区域形成较大直径的气泡。气泡尺寸沿径向逐渐降低并变化趋于平缓。气液界面浓度在冷却管外壁面附近出现较大值，并且沿径向逐渐降低并趋于稳定。

［1]Mycock J C， Mckenna J D， Theodore L. Handbook of air pollution control engineering and technology［M］. New York: CRC Press， 1995: 133-171.

［2]金 刚， 王亦飞， 路文学. 新型洗涤冷却室结构的应用［J］. 大氮肥， 2007， 30（5）: 358-360. Jin Gang， Wang Yifei， Lu Wenxue. Application of new structure of scrubbing cooler chamber［J］. Large Scale Nitrogenous Fertilizer Industry， 2007， 30（5）: 358-360.

［3]赵永志， 顾兆林， 李 云， 等. 水煤浆气化炉激冷室下降管内流动与传热数学模拟［J］. 化工学报， 2003， 54（1）: 115-118. Zhao Yongzhi， Gu Zhaolin， Li Yun， et al. Numerical simulation on turbulent flow and heat transfer of vertical pipe in quench chamber of coal gasifier［J］. Journal of Chemical Industry and Engineering， 2003， 54（1）: 115-118.

［4]吴 晅，高靖芳，武文斐， 等. 气化炉洗涤冷却室内气液两相流动特性的数值模拟［J］. 热力发电， 2012， 41（4）: 23-29. Wu Xuan， Gao Jingfang， Wu Wenfei， et al. Numerical simulation of flow behavior concerning gas-liquid two-phase turbulence in scrubbing-cooling chamber of the gasifier［J］. Thermal Power Generation， 2012， 41（4）: 23-29.

［5]吴宏涛. 新型洗涤冷却室内洗涤冷却管振动及气液流动研究［D］. 上海: 华东理工大学， 2007.

［6]贺必云. 新型洗涤冷却室内多相流动特征的研究［D］. 上海: 华东理工大学， 2005.

［7]许 杰. 洗涤冷却室内流动及热质传递过程研究［D］. 上海: 华东理工大学， 2005.

［8]陈意心， 王亦飞， 梁 铁， 等. 新型洗涤冷却室内气液两相的分布特性［J］. 化工学报， 2008， 59（2）: 323-327. Chen Yixin， Wang Yifei， Liang Tie， et al. Characteristics of phase distribution of gas-liquid two-phase flow in new scrubbing-cooling chamber［J］. Journal of Chemical Industry and Engineering， 2008， 59（2）: 323-327.

［9]龚晓波， 顾兆林， 林高平， 等. 水煤浆气化炉激冷流程中气液两相负浮力流动的数值模拟［J］. 化工学报. 2003， 54（7）: 930-935. Gong Xiaobo， Gu Zhaolin， Lin gaoping， et al. Numerical simulation of gas-liquid two-phase flow with reverse buoyancy in quench chamber of coal gasifier and its application［J］. Journal of Chemical Industry and Engineering， 2003， 54（7）: 930-935.

［10]谢海燕， 袁竹林. 激冷室内合成气穿越液池过程流动特性与带水问题［J］. 中国电机工程学报， 2007， 27（8）: 37-41. Xie Haiyan， Yuan Zhulin. Flowing characteristics and problem of entraining water about mixed gas crossing the cistern in quench chamber［J］. Proceedings of the CSEE， 2007， 27（8）: 37-41.

［11]Yeoh G H， Tu J Y. Population balance modeling for bubbly flows with heat and mass transfer［J］. Chemical Engineering Science， 2004，59（15）: 3125-3139.

［12]Montante G， Horn D， Paglianti A. Gas-liquid flow and bubble size distribution in stirred tanks［J］. Chemical Engineering Science， 2008，63（8）: 2107-2118.

［13]宋庆唐， 金家琪， 吴桂英， 等. 二维鼓泡床内气泡尺寸分布的实验与CFD模拟［J］. 化工学报， 2008， 59（2）: 335-340. Song Qingtang， Jin Jiaqi， Wu Guiying， et al. Experiment and CFD simulation of bubble size distribution in 2D gas-liquid bubble column［J］. Journal of Chemical Industry and Engineering （China）， 2008， 59（2）: 335-340.

［14]杨立新， 巴黎明， 李 星. 两种气液两相流模型的应用和比较［J］. 工程热物理学报， 2007， 28（2）: 93-96.Yang Lixin， Ba Liming， Li Xing. The application and comparison between two kind of gas-liquid numerical models［J］. Journal of Engineering Thermophysics， 2007， 28（2）: 93-96.

［15]Cheung S C P， Yeoh G H， Tu J Y. On the modeling of population balance in isothermal vertical bubbly flows-average bubble number density approach［J］. Chemical Engineering and Processing， 2007， 46（8）: 742-756.

［16]Sherman C P， Yeoh G H， Tu J Y. On the numerical study of isothermal vertical bubbly flow using two population balance approaches［J］. Chemical Engineering Science， 2007， 62 （17）: 4659-4674.

［17]Yeoh G H， Tu J Y. Numerical modeling of bubbly flows with and without heat and mass transfer［J］. Applied Mathematical Modeling，2006， 30（10）: 1067-1095.

［18]Krishna R， Baten J M. Mass transfer in bubble columns［J］. Catalysis Today， 2003， 79（30）: 67-75.

［19]Deen N G， Solberg T， Hjertager H B. Large eddy simulation of the gas-liquid flow in a square cross-sectioned bubble column［J］. Chemical Engineering Science， 2001， 56（21）: 6341-6349.

［20]Drew D A， Lahey R T Jr. The virtual mass and lift force on a sphere in rotating and straining in viscid flow［J］. Int J Multiphase Flow，1987， 13: 113-121.

［21]Buwa V V， Ranade V V. Dynamics of gas-liquid flow in a rectangular bubble column: experiments and single/group CFD simulations［J］. Chemical Engineering Science， 2002， 57（22）: 4715-4736.

［22]Wu Q， Kim S， Ishii M. One-group interfacial area transport in vertical bubbly flow［J］. International Journal of Heat and Mass Transfer，1998， 41（8/9）: 1103-1112.

［23]Hibiki T， Ishii M， Xiao Z. Axial interfacial area transport of vertical bubbly flows［J］. International Journal of Heat and Mass Transfer，2001， 44（10）: 307-328.

［24]Hibiki T， Lee T H， Lee J Y， et al. Interfacial area concentration in boiling bubbly flow systems［J］. Chemical Engineering Science， 2006，61（24）: 7979-7990.

［25]Yao W， Morel C. Volumetric interfacial area prediction in upward bubbly two-phase flow［J］. International Journal of Heat and Mass Transfer， 2004， 47（2）: 307-328.

Numerical Simulation on Characteristics of Bubbles in Process of Gas Passing Through Pool Base on Bubble Number Density Model

Wu Xuan1，2， Jiao Jinjin2，Wang Lifang2， Jin Guang2
1. Inner Mongolia Key Laboratory of Integrated Exploitation of Bayan Obo Multi-Metallic Resources， Inner Mongolia University of Science and Technology， Baotou 014010， China；2. School of Energy and Environment， Inner Mongolia University of Science and Technology， Baotou 014010， China

An average bubble number density （ABND） transport equation considering bubbles breakup and coalescence was merged with the Euler-Euler turbulence two-fluid model in the Computational Fluid Dynamics （CFD） to establish the CFD-ABND coupling model which was used to study the bubble size distribution and the interfacial area concentration （IAC） distribution in the pool when the gas-solid flow passed through the pool. The quantitative results of bubbles size and IAC distribution were observed， and the influence of gas velocity on the distribution of the bubble and the IAC was analyzed. It was found that the present model had a better performance for predicting the bubble size and IAC distribution. The results showed that the larger bubble and the higher IAC mainly existed near the exit and outer wall of the cooling tube. The separator inserter IAC in the pool was very helpful to strengthen the disturbance between gas and liquid， which could effectively reduce the bubble size and increase the IAC.

gasifier； scrubbing-cooling chamber； bubble size； interfacial area concentration； numerical simulation

TQ546.5

A

1001—7631 （ 2015 ） 02—0115—08

2014-06-12；

2014-12-09。

吴 晅（1976—），男，博士，副教授。E-mail: wxgjf@163. com。

国家自然科学基金（51166010）；内蒙古自治区自然科学基金（2014MS0530）；内蒙古科技大学创新基金资助项目（2011NCL020）。