水面LNG液池扩展模型的分析与对比研究*
2018-04-13陈旭芳李云涛
陈旭芳,李云涛,帅 健
(中国石油大学(北京) 机械与储运工程学院,北京 102249)
0 引言
液化天然气(LNG)作为清洁能源在全球贸易中的地位越来越重要[1]。船运是液化天然气运输的主要方式之一。自20世纪五十年代第一艘液化天然气运输船“甲烷先锋号”成功航行以来,全球液化天然气运输船数量不断增多,且单船运输量也不断增加[2],其安全问题引起了广泛关注。
当LNG船舶发生碰撞、搁浅或恐怖袭击等事件时,储罐内的LNG可能发生泄漏,在水面上形成液池并进行扩展[3],由于LNG储存温度较低,LNG和水面的温差较大,导致LNG不断蒸发并形成蒸气云团,若蒸气云团被点燃,容易引发爆炸事故,后果不堪设想;此外,如果LNG液池被点燃,则极易形成池火或流淌火,其辐射传热会对周围人员、船舶及设备设施造成伤害。由于LNG的蒸发消耗速率(即单位时间内液池蒸发的质量,蒸气云团的释放源项)和池火直径的计算均需以液池扩展半径为基础。因此,分析LNG液池的扩展情况对于LNG泄漏的火灾和蒸气云爆炸后果评价都有着现实意义。
过去几十年,国内外学者对液池扩展进行了大量的研究,并取得了一定成果。目前,针对LNG扩展的研究成果主要包括基于“重力-惯性”平衡的Fay模型、考虑了摩擦力作用的FERC模型、SNL模型等分析模型,以及Fluent、FLACS等计算流体力学软件[4-8]。这些方法的假设条件不尽相同,计算结果差异较大。由于LNG实验具有一定的危险性,上述方法很少能得到实验数据验证。目前虽有针对FERC等分析模型的对比研究[9],但对分析模型和计算流体力学软件的计算结果对比较少。
本文通过对比被广泛接受的Fay模型、FERC模型和FLACS软件模拟3种方法,讨论LNG在水面泄漏后的液池半径随时间的动态变化过程,并对火灾后果进行分析,其结果或可为LNG泄漏事故的火灾后果评价提供参考。
1 模型介绍
Fay[4]认为当泄漏量较大时,液池在“重力-惯性”平衡的作用下扩展。该模型假设油膜厚度均匀分布,液池半径的变化情况表示为:
(1)
式中:r为液池半径,m;t为时间,s;β为经验常数,取2.31;g为重力加速度,取9.81 m/s2;Δ= (ρw-ρL)/ρw,表示水面以上油膜所占的比例,其中ρw和ρL分别为水和LNG的密度,kg/m3;h=VP/AP为油膜平均厚度,m;AP为液池面积,m2;VP为液池体积,m3。根据质量守恒:
(2)
式中:Qin为LNG泄漏速率,m3/s;mv为蒸发速率(若对池火灾或流淌火分析,则为燃烧速率),kg/(m2·s)。
在美国联邦能源管理委员会(FERC)的资助下,ABS Consulting[10-11]采用了基于Webber模型的液池扩展模型,考虑了摩擦力和油膜形状对液池扩展的影响,其质量守恒方程与Fay模型相同,见公式(2),液池半径的变化情况表示为:
(3)
式中:Φ为形状因子,与hf/h有关,hf为前沿油膜厚度,m;h为油膜平均厚度;CF为摩擦阻力(层流或湍流阻力),m/s2。
FLACS是挪威Gexcon公司开发的用于计算物质泄漏扩散、爆炸及火灾后果的计算流体力学(CFD)软件,其中,基于二维浅水方程的液池模块(POOL)可用于分析低温液体泄漏后的液池扩展及蒸发过程[12],质量方程和动量方程分别见公式(4)和公式(5)。
(4)
(5)
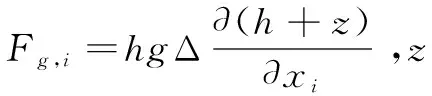
综上所述,Fay模型、FERC模型和FLACS模拟均通过质量方程和动量方程来确定液池的扩展情况。在LNG液池扩展的分析中,计算结果受泄漏量、泄漏速率、泄漏时间等因素控制,以下对不同泄漏方式下的液池扩展情况进行分析。
2 液池扩展分析
LNG船舶发生泄漏时,LNG会在水面形成液池,由于船体等的阻挡,液池在水面上近似呈半圆形。为方便对比,本文在使用3种方法进行对比分析时,采用相同的蒸发速率和泄漏速率。FLACS软件的POOL模块中内置了液池的蒸发模型,蒸发速率可根据水面温度、太阳辐射等因素自动计算,故此处仅对Fay模型和FERC模型中的蒸发速率进行设定,均选用FERC模型中推荐值0.17 kg/(m2·s),即China Lake试验中得到的蒸发速率[13]。
泄漏LNG液池的扩展受泄漏方式等因素的影响,液体的泄漏方式根据泄漏口孔径由小到大可以分为恒速泄漏、变流速泄漏和瞬间泄漏。当泄漏孔径非常小时,泄漏速率几乎不随时间变化,可视为恒速泄漏[14]。本文主要对变流速泄漏和恒速泄漏时液池的扩展情况进行分析。
为了更好地对比分析Fay模型、FERC模型和FLACS软件模拟3种方法的液池扩展情况,本文设定2个模拟方案:
1)容量为12 500 m3的LNG从孔径分别为1 m和5 m的储罐破裂口泄漏,储罐内泄漏口以上LNG初始液位为13 m;
2)LNG以1 m3/s恒速持续泄漏。
2.1 变流速泄漏
一定量的液体从泄漏口泄漏时,其泄漏速率可通过孔口模型得到:
(6)
式中:Q(t) 为t时刻的泄漏速率,m3/s;Cd为泄漏系数,通常取0.65;g为重力加速度,m/s2;h(t)为t时刻容器中液位高度,m;Ah为泄漏口面积,m2。
当泄漏口孔径为1 m时,泄漏共持续3 066 s,泄漏后的液池半径随时间的变化曲线由图1所示。在此种泄漏模式下,3种方法所计算的液池蒸发所需时间均等于泄漏持续时间,即泄漏停止时,液池全部蒸发。在泄漏初期,因液池面积较小,泄漏速率大于蒸发消耗速率,液池内的LNG体积增加,液池迅速扩展;随着液池面积的增大,消耗速率开始大于泄漏速率,液池内的LNG体积减小,液池深度下降,并最终停止扩展。此后,泄漏速率与消耗速率达到动态平衡,液池面积等于泄漏速率除以蒸发速率,液池随泄漏速率的减小而逐渐收缩。在此过程中,存在最大的液池扩展面积。Fay模型、FERC模型和FLACS软件模拟得到的最大液池半径值分别为158.27,126.46和112.87 m,以FLACS模拟结果为参照,Fay 模型、FERC 模型的最大液池半径分别比FLACS 软件模拟结果大40.22%和 12.04%。
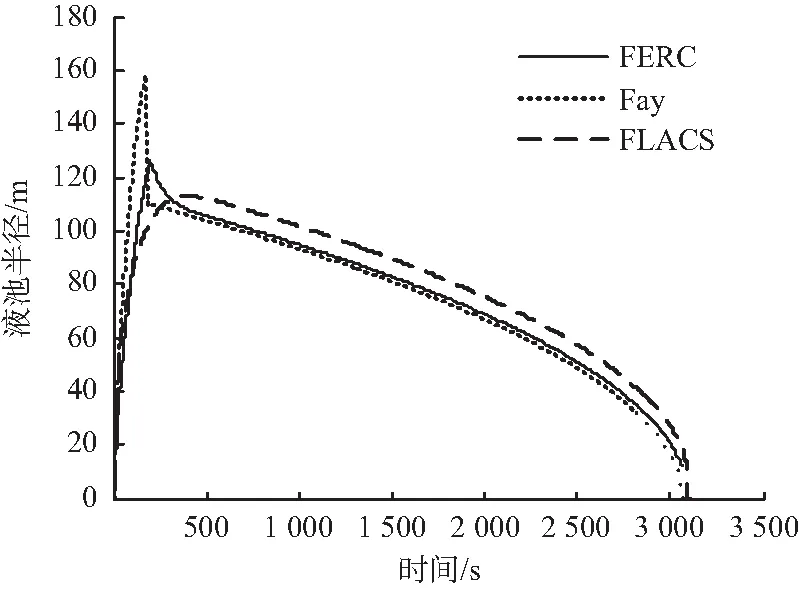
图1 泄漏孔径为1 m时的LNG液池半径变化情况Fig.1 Pool radius versus time for 1 m diameter release
泄漏口孔径为5 m时,泄漏共持续120 s,泄漏后的液池半径随时间的变化曲线由图2所示。3种方法得到的液池蒸发所需时间均大于液池泄漏持续时间,即在泄漏停止后,液池仍在扩展,直至达到最大值。Fay模型、FERC模型和FLACS软件模拟得到的最大液池半径分别为398.27,346.04和289.24 m,其中Fay模型和FERC模型的最大液池半径分别比FLACS模拟结果大37.70%和19.64%。
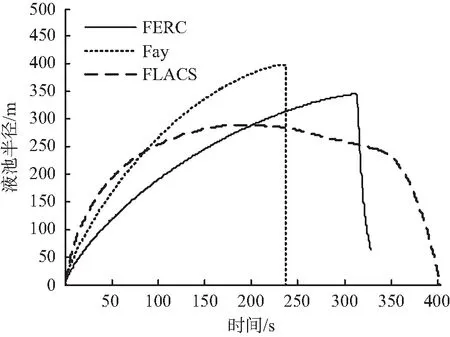
图2 泄漏孔径为5 m时的LNG液池半径变化情况Fig.2 Pool radius versus time for 5 m diameter release
综上可知,泄漏量相同情况下,Fay模型、FERC模型和FLACS软件模拟得到的最大液池半径值依次减小。这是由于在Fay模型中忽略了摩擦阻力的影响,因此,其计算的液池扩展速率偏大。当泄漏孔径比较小时(1 m),3种方法得到的液池收缩过程基本一致,此时的液池面积均等于泄漏速率除以蒸发速率。由于FLACS中的蒸发速率(约0.143 kg·m-2·s-1)是根据环境条件由沸腾模型计算所得,其值较Fay模型和FERC模型中所采用的实验值(0.17 kg·m-2·s-1)偏低,因此在收缩阶段FLACS所示的液池半径较大。当泄漏孔径较大时(5 m),3种方法中液池蒸发时间均大于泄漏持续时间。如前所述,Fay模型的液池面积较大,因此其持续时间较短。
2.2 恒速泄漏
当泄漏孔径非常小时,泄漏可视为恒速泄漏,此处设定LNG以1 m3/s 持续泄漏,其液池半径变化情况如图3所示。
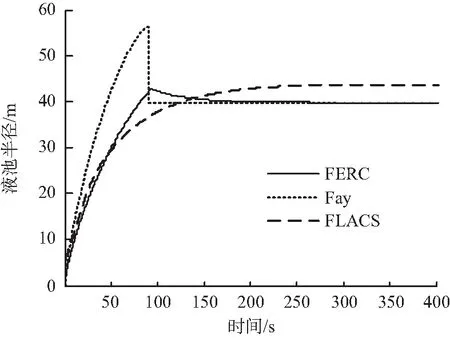
图3 泄漏速率为1 m3/s时的LNG液池半径变化情况 Fig.3 Pool radius versus time for 1 m3/s release rate
在此过程中,Fay模型、FERC模型和FLACS等3种方法计算的最大液池扩展半径分别为:56.25,42.78和43.67 m,FLACS的结果略大于FERC模型计算结果。由图可知,Fay模型和FERC模型计算得到的液池变化情况基本一致。在泄漏初期,液池在重力作用下扩展,面积不断增大,因蒸发而引起的消耗速率(蒸发速率×液池面积)不断增加;当消耗速率大于泄漏速率时,液池扩展速率开始减小,液池厚度也逐渐减小。液池前沿处的LNG首先蒸发完毕,在视觉上体现为液池收缩。随着液池面积的减小,液池消耗速率逐渐减小,当其与泄漏速率相等时,液池达到动态平衡,此时液池面积为一稳定值,即泄漏速率(1 m3/s)除以蒸发速率(0.17 kg·m-2·s-1)。由于Fay模型中假设液池厚度均匀分布,故其液池收缩是一个突变过程;而FERC模型中考虑了液池深度的不均匀分布,故该过程为渐变过程。液池面积的小幅收缩与流淌火的实验现象相符[15],因此FERC模型更加接近真实。Fay模型和FERC模型的另一个区别还在于,在FERC模型中,存在能够使LNG扩展的最小液池深度(1 mm),当液池深度小于该临界值时,重力与表面张力平衡,流动停止并进入准稳态阶段。而Fay模型中却仅当液池中的LNG完全蒸发后才停止流动。这也在一定程度上导致其计算的最大液池半径较FERC模型偏大。
由于FLACS是在二维浅水方程的基础上计算的,难以处理干-湿区域界限,因此其模拟的结果中不存在液池的小幅度收缩过程。液池在重力等作用下扩展,液池蒸发速率逐渐增大,当蒸发速率等于泄漏速率时,液池达到稳态平衡,此时液池达到稳态,不再继续扩展。
图4表示恒速长时间的泄漏条件下液池最大半径与泄漏速率的变化情况,其中Fay模型得到的液池最大半径最大。结合图3,当泄漏速率为1 m3/s时,Fay模型得到的最大半径值最大,FERC模型计算得到的结果略小于FLACS软件模拟结果;当泄漏速率大于1 m3/s时,FLACS软件模拟结果较FERC模型计算的最大半径值偏小。
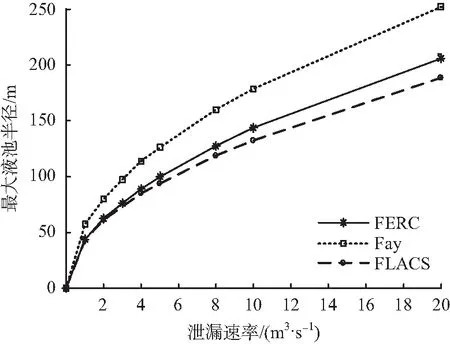
图4 泄漏速率对最大液池半径的影响Fig.4 Effect of release rate on the maximum pool radius
泄漏速率不同时,相应的液池最大半径变化情况如表1所示。
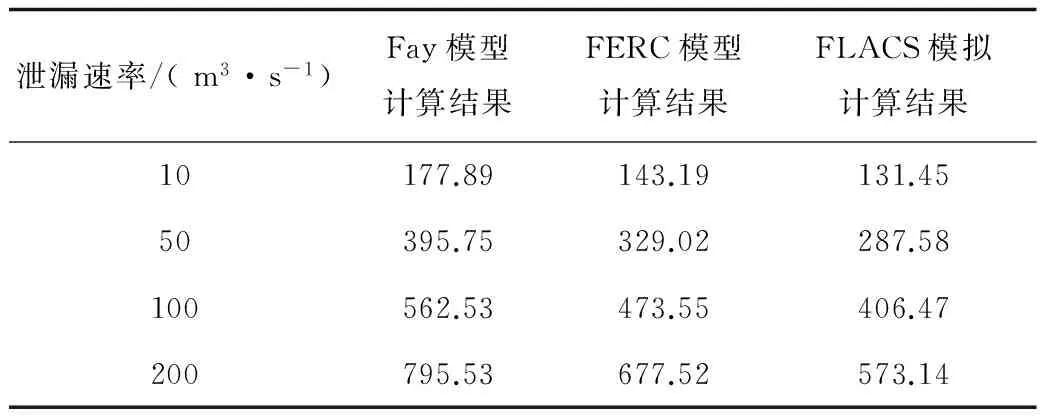
表1 泄漏速率不同时的液池最大半径 /m
由表1可以看出,当泄漏速率为50 m3/s 时,Fay模型和FERC模型分别比FLACS模拟结果大37.61%和14.41%;当泄漏速率为 100 m3/s 时,Fay模型和FERC模型分别比FLACS模拟结果大38.39%和16.50%;当泄漏速率为 200 m3/s 时,此比例变为38.80%和18.21%。据此可知,当泄漏速率增加时,Fay模型和FLACS模拟的结果之间相对差值变化较小,FERC模型和FLACS模拟的结果之间的相对差值有小幅度的增加。
通过对比可以发现,FERC模型中考虑了摩擦阻力、最小液池深度等因素,因此其计算的液池扩展速率和液池半径等均较相同条件下的Fay模型计算结果偏低,但其计算结果更接近FLACS的模拟结果。考虑到CFD软件价格昂贵,且计算耗时较大,因此在一般的工程应用时,采用FERC模型即可方便快捷地获得较为准确的结果。但是,需要指出的是,Fay模型和FERC模型仅适用于静止的水平表面,如要计算高低起伏的地面LNG液池扩展,或还需借助于CFD软件。
3 火灾后果评价
为了研究液池扩展可能造成的最大火灾后果,假设液池达到最大半径时被点燃,分析火焰辐射对周围环境的影响。
在进行火灾辐射评价时,常需要池火的直径、火焰高度和燃烧速率等参数。池火直径可由液池扩展的计算结果给出。由于池火直径较大,此时燃烧速率与直径无关[16],此处采用为FERC模型中的推荐值0.282 kg/(m2·s)[10]。火焰高度则采用Mudan模型中无风情况下的公式[17]进行计算:
(7)
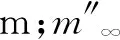
假设LNG以恒定1 m3/s的恒速泄漏,不考虑风的作用。由图3可知,Fay模型、FERC模型和FLACS软件模拟得到的最大液池半径分别为56.25,42.78和43.67 m。
由式7可计算得到,Fay模型、FERC模型和FLACS对应的火焰高度分别为:220.32,182.15和184.78 m。
通过Mudan模型[17]计算可以得到,液池在达到最大半径时被点燃,目标接受的热辐射通量随目标与火焰中心距离的变化情况如图5所示。
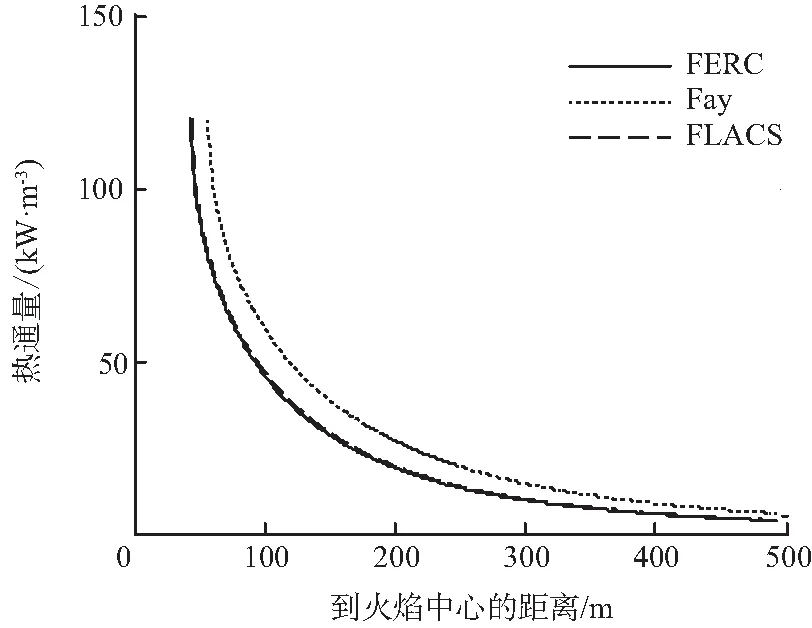
图5 发生流淌火时目标接受的热辐射通量Fig.5 Heat flux versus distance during pool fire
由图5可知,相同距离下,通过FERC模型和FLACS模拟的最大值计算得到的辐射通量值相近,Fay模型得到的辐射通量相对较大;同时,在远离火焰中心处,3种方法得到的热辐射强度差值较小。
结合热辐射的破坏和伤害准则[18],选取 4kW/m2作为人员轻伤的极限值,此时,3种方法得到的目标到火焰中心的最小安全距离分别为602.75,480.68和488.97 m。由此可见,Fay模型得到的最小安全距离的范围最大,其结果偏保守,而FERC模型与FLACS的模拟结果更为接近。
4 结论
1)等量泄漏时,Fay模型、FERC模型和FLACS软件得到的最大液池半径值依次减小;当泄漏孔径较小时,3种方法的计算结果均存在液池收缩过程,此时的液池面积等于泄漏速率除以蒸发速率。
2)恒速持续泄漏时,Fay模型和FERC模型得到的液池扩展过程均包括液池扩展、小幅度收缩和动态平衡3个阶段,这与实验结果相符,但FLACS结果中不包括小幅度收缩过程。
3)相同泄漏条件下,FERC模型的计算结果与FLACS的模拟结果接近且偏于保守,考虑到其经济性与便利性,推荐在一般工程应用时使用。
4)相同泄漏条件下,Fay模型计算得到的液池最大半径值最大。因此,在开展火灾热辐射评价时,若采用Fay模型,其结果将更为保守;在实际的低温液体泄漏扩展中,环境风、地形等便捷条件对液池扩展和火灾后果均会产生一定影响,在今后研究中有待进一步完善。
[1]BP. BP世界能源统计年鉴[R].英国: BP公司, 2017.
[2]庄学强,高孝洪,孙迪. 液化天然气船舶事故性泄漏扩散过程综述[J]. 中国航海, 2008, 31(3):280-283.
ZHUANG Xueqiang,GAO Xiaohong,SUN Di. Research on Accidental Leakage and Diffusion Process of LNG Vessel [J]. Navigation of China, 2008, 31(3): 280-283.
[3]HISSONG D W. Keys to modeling LNG spills on water[J]. Journal of Hazardous Materials, 2007, 140(3): 465-477.
[4]FAY J A. Model of spills and fires from LNG and oil tankers[J]. Journal of Hazardous Materials, 2003, 96(2/3): 171-188.
[5]JOHNSON D W, CORNWELL J B. Modeling the release, spreading, and burning of LNG, LPG, and gasoline on water[J]. Journal of Hazardous Materials, 2007, 140(3): 535-540.
[6]SANDIA National Laboratories. Guidance on risk analysis and safety implications of a large liquefied natural gas (LNG) spill over water[R]. SAND 2004-6258, 2004:12.
[7]GAVELLI F, BULLISTER E, KYTOMAA H. Application of CFD (fluent) to LNG spills into geometrically complex environments[J]. Journal of Hazardous Materials, 2008, 159(1): 158-168.
[8] 林小侦,于光认, 魏利军,等. 液化天然气在水面地面扩散对比研究[J]. 中国安全生产科学技术,2014,10(8): 86-90.
LIN Xiaozhen, YU Guangren, WEI Lijun, et al. Comparative study of LNG dispersion on water and ground [J]. Journal of Safety Science and Technology, 2014, 10(8): 86-90.
[9]OKA H, OTA S. Evaluation of consequence assessment methods for pool fires on water involving large spills from liquefied natural gas carriers[J]. Journal of Marine Science and Technology, 2008, 13(2): 178-188.
[10]ABS Consulting Inc. Consequence assessment methods for incidents involving releases from liquefied natural gas carriers [R].Houston: ABS Consulting Risk Consulting Inc.,2004.
[11]Federal Energy Regulatory Commission. Notice of availability of staff’s responses to comments on the consequences assessment methods for incidents involving releases form liquefied natural gas carriers[R]. FERC, 2004.
[12]ICHARD D, HANSEN O R, MIDDHA P, et al. CFD computations of liquid Hydrogen releases[J]. International Journal of Hydrogen Energy, 2012, 37(22): 17380-17389.
[13]RAJ P K. LNG fires: A review of experimental results, models and hazard prediction challenges[J]. Journal of Hazardous Materials, 2007, 140(3):444-464.
[14]何思念,常华伟,文科,等.液化天然气泄漏和水面扩散过程模拟[J].化工学报,2015,66(S2):213-219.
HE Sinian, CHANG Huawei, WEN Ke, et al. Mathematical modeling of LNG spills and pool spreading on water[J]. CIESC Journal,2015,66(S2):213-219.
[15]LI Yuntao, HUANG Hong, WANG Zheng, et al. An experimental and modeling study of continuous liquid fuel spill fires on water[J]. Journal of Loss Prevention in the Process Industries,2015,33(33): 250-257.
[16]BLINOV V I, KHUDYAKOV G N. Diffusion Burning of Liquid[J]. Diffusion Burning of Liquids, 1961, 762.
[17] HURLEY M J, GOTTUK D T, JR J R H,et al. SFPE Handbook of Fire Protection Engineering[M]. Springer New York, 2016: 2612-2614.
[18]傅智敏, 黄金印, 付敏. 烃类流体火灾伤害破坏作用定量分析[J]. 中国安全科学学报, 2008, 18(9):29-36.
FU Zhimin, HUANG Jinyin, FU Min. Quantitative analysis of thermal radiation damaging effects caused by liquid or gaseous hydrocarbon fires[J]. China Safety Science Journal, 2008,18(9):29-36.
