数学与专业课如何有机结合

范雪莲

摘    要： 如今，在经济危机这样严峻的形势下，各类学生的就业情况，属职教类毕业生最好。其主要原因是，职教类学校重技能训练，按照企业的要求，制订教学计划，开设课程，加强专业课的实际训练，学生的技能水平大大提高，一毕业就能上岗操作，因而深受企业欢迎，在就业市场赢得了主动权。

关键词： 职业高中    数学应用    电工专业

在职业高中开设课程，除了专业课以外，还要开设必要的文化课。如何安排好科目之间的关系，对于学生学习起到了至关重要的作用。下面针对专业特征谈谈数学在电工专业中的应用。

一、数学应用的广泛性

数学的主要特征之一，就是应用的广泛性。“广泛”对现代数学来说就是人类活动，人类科学的几乎所有的领域都要应用数学，与其他科学相比，这是十分独特的。数学产生于人的实践之中，即数学是在人的应用需要中发展起来的。萌芽时期的数学都具有直接的应用性，近代数学的大发展是由数学在科学技术中的应用开始的，应用促进了微积分学的产生（17世纪），此后分析数学、统计数学的发展都与应用有着直接的关系。随着数学的发展，数学的应用能力不断提高——不断提供更有力的工具，因而可能在更广泛的领域得到应用。

数学的应用为什么如此广泛？那就是因为数学对于人的实践和其他科学具有下述重要意义：数学为各领域的问题及其解决提供了科学的表述语言;为其他科学提供了一种抽象思维的模式，即充分发挥人的主观能动性和创造性思维能力，解决各种现实问题的途径;为解决各领域的问题提供计算方法。

二、职业高中数学教学的现状

职高学生从小学到现在长时间的数学学习过程中，普遍存在概念不清、推理不严谨等问题，没有合理的知识结构，故而对数学产生厌恶和排斥情绪。同时学生学习目标不够明确，任务观点，未能切实感受到数学在他们专业上的用途，以至于不思上进，甚至于以破坏课堂纪律来反抗，作业不认真，抄袭应付，学生学得很无奈。对于数学老师而言，也是竭尽了全力，疲于奔命，可是却收效甚微，徒劳无功。久而久之，形成恶性循环，导致教学失败。

如何改变现状呢？着眼于数学和电工专业的结合，使学生切实感受数学的重要性，能够重视数学，提起对数学的学习兴趣。

三、如何将数学应用到专业课中

不同专业课教学所用到的数学基础知识是不同的。为提高课堂教学效率，必须将数学课程与专业课程资源有效整合。具体做法是：钻研教材，寻找关联知识;总结、提炼出两个学科教学中相通的数学思想方法;创设问题情境，复习旧知、联系新知，区分数学知识在电工专业中具体应用的不同点;由专业课需求确定数学教学的重、难点。

1.应用数学的函数图像

函数可以通过坐标系转化成图形，从而直观地研究。数和形是数学的两大根基，以前毫不相干，正是坐标系的出现，把作为“数”的函数转化为作为“形”的图像，从此数学发展得更蓬勃。把函数解析式表示成图像，我们能从中获取很多信息。直接地说，能从函数图像上看出函数的变化趋势，形象化对解题起到非常重要的作用。

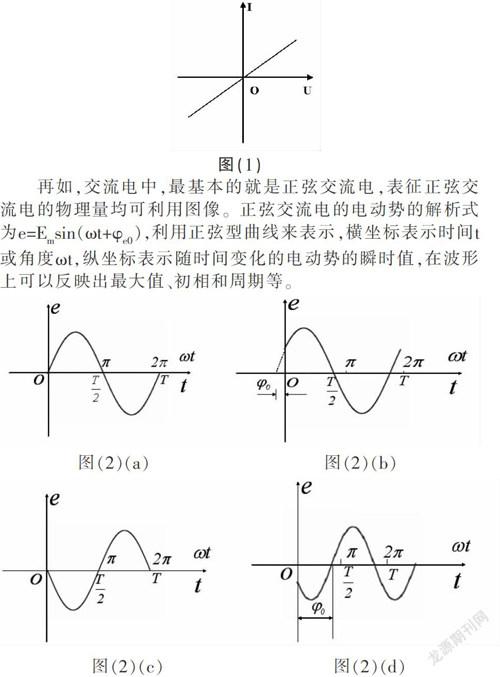
例如，可以用图像表示电压与电流的关系。如图，以电压为横坐标，电流为纵坐标，可画出U-I关系曲线，称为电阻元件的伏安特性曲线，如图（1）所示。当电阻元件伏安特性曲线是直线时，称为线性电阻。即此电阻元件的电阻值R可以认为是不变的常数，直线斜率的倒数表示改电阻元件的电阻值。如果不是直线，则成为非线性电阻。利用图像，就可很直观地看出电阻是否是线性电阻。

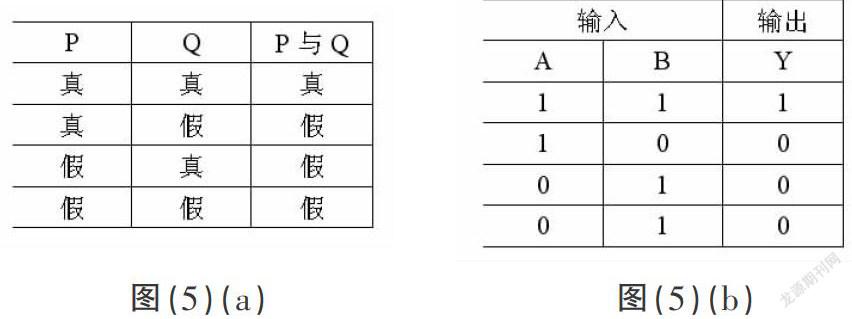
再如，交流电中，最基本的就是正弦交流电，表征正弦交流电的物理量均可利用图像。正弦交流电的电动势的解析式为e=Esin（ωt+φ），利用正弦型曲线来表示，横坐标表示时间t或角度ωt，纵坐标表示随时间变化的电动势的瞬时值，在波形上可以反映出最大值、初相和周期等。

图（2）（a）                                      图（2）（b）

图（2）（c）                                     图（2）（d）

如图（2）（a）正弦曲线的初相为零，图（b）的初相在0～π之间，图（c）的初相在-π～0之间，图（d）的初相为±π。在分析初相时，如果借助了正弦曲线，就可很形象地看出，如果初相是正值，曲线的起点就在坐标原点的左边;如果初相是负值，则起点在原点的右边。为了比较几个正弦量的相位关系，也可以把它们的曲线画在同一坐标系内。但由于它们的单位不同，故纵坐标上电压、电流可分别按照不同比例表示。三相对称电动势的表示上，正弦曲线的优势更能够体现出来。若以第一相电动势的初相角为0°，则第二相为-120°，第三相为120°，那么各相电动势的瞬时值表达式则为

e=Esinωt，e=Esin（ωt-120°），e=Esin（ωt+120°）。

如图（3），从图像上很容易看出，三相对称电动势在任一瞬间的代数和为零。

图（3）

从一系列实例上也可看出，数学的图像对于电工中某些物理量的表示起到了极其重要的作用，能加深学生的理解，也能简化某些概念的表述。

2.应用数学的空间想象力

培养空间想象力是数学教学的主要任务之一。在《电工基础》这本教材上，对于电磁感应这个章节的内容，就需要应用数学中的空间想象能力。在用右手定则判断感应电流方向及用左手定则判断感应电动势的时候，就要利用空间想象力，图上只能画出二维的图形，对于三维图形，如果没有扎实的数学功底，是很难办到的。

3.应用数学的逻辑思维能力

逻辑学是研究思维形及思维规律的科学，思维的形式包括概念、判断和推理之间的结构和联系。概念是思维的基本单位，通过概念决定事物是否具有某种属性就是判断，由判断推出另一个判断的思维形式就是推理。用数学的方法研究推理就是数学逻辑。在中学数学教学中，也有很多相关逻辑的内容。在学习逻辑内容时，前提是要熟悉逻辑连接词。在数字电路中，同样也有逻辑电路。下面谈谈这些简易逻辑代数在电工中的应用。

（1）非

数学中对于非得表述：对于每一个命题，都有一个与它意义相反的命题，这个命题就是原来命题的否定，其真值表见图（4）a。电路中的非门电路，是指输出信号与输入信号存在着“反相”关系，即输入信号为低电平时，输出信号为高电平;而输入信号为高电平时，输出信号为低电平。非门只有一个输入端和输出端。比如输入为1，则输出为非1，即0;反之，输入为0，则输出为非0，即1。非门的真值表见图（4）b。

图（4）（a）                             图（4）（b）

（2）与

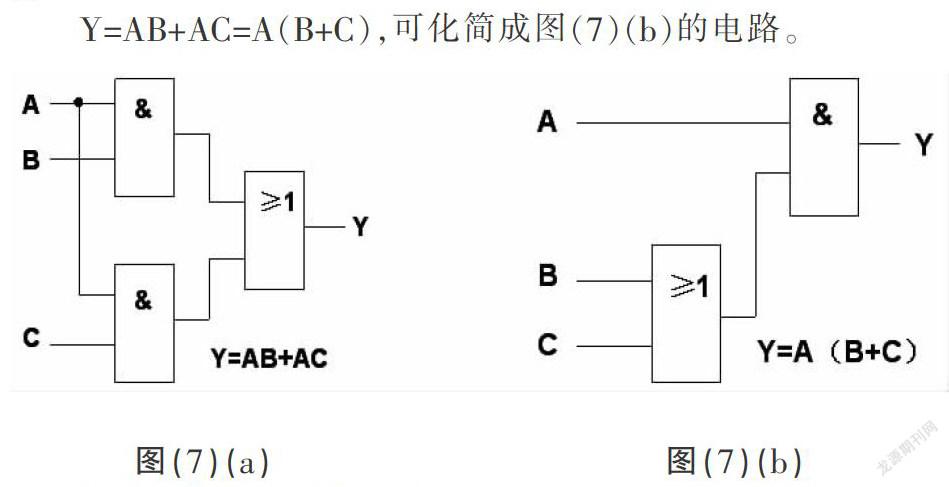
设P和Q是两个命题，“P与Q“真值表见图（5）a。电路中的与门电路假如有两个输入端A和B，一个输出端Y，Y=AB其真值表见图（5）b。与门电路的输入端可以个有多个，只有当输入端全为1时，输出才为1，其余都是0.

图（5）（a）                                       图（5）（b）

（3）或

设P和Q是两个命题，“P或Q”真值表见图（6）a。电路中的或门电路，假如有两个输入端A、B，有一个输出端Y=A+B，其真值表见图（6）b。同样，或门电路也可以由多个输入端，只有当输入端全为0时，输出端才为0，i其余都是1.

图（6）（a）                                   图（6）（b）

光从概念看，数学和电工是统一的。那么怎么体现出数学逻辑的优越性呢？各个逻辑组合起来有规定的运算法则。例如：=P，=∨，=∧，将这一系列运算法则运用到组合逻辑门电路中，它的优势能得以体现了。常见的简单组合门有：与非门Y=;或非门y=;与或非门y=等。在这些组合门中，利用逻辑代数运算法则，得其真值表，能够简便而正确地得知输出端的情况。逻辑代数是研究逻辑电路的数学工具，利用逻辑代数可以判定一个已知逻辑电路的功能或根据需要的逻辑功能研究和简化一个相应的逻辑电路。任何组合逻辑电路其输入和输出状态的逻辑关系可用逻辑函数式表示，反之，任何一个逻辑函数式，总可以用组合逻辑电路与之对应。由于逻辑代数有一些基本的运算定律，应用这些定律可以把一个复杂的逻辑函数式恒等化简。由于每一个逻辑函数式都体现着一个电路，因此逻辑函数式的化简就意味着电路的化简。可见逻辑代数的作用，就在于把逻辑电路的简化问题变成相应的逻辑函数式的简化问题，为设计和认识逻辑电路带来方便。

例如：设计一个体现Y=AB+AC函数式的逻辑电路。

解：根据题意，可画出图（7）（a）的电路，但函数式化简后得

Y=AB+AC=A（B+C），可化简成图（7）（b）的电路。

图（7）（a）                                            图（7）（b）

4.应用数学的运算公式

数学的公式众多，是一切运算的基本工具。在电工专业中更应该灵活运用数学公式。比如，可以用复数表示正弦交流电，具体方法如下：用复数的模表示正弦电压或电流的有效值，用辐角表示正弦电压或电流的初相角。

例如：已知两个正弦交流电流为

i=6sin（ωt+120°）A，i=8sin（ωt+30°）A，求它们的和。

解：i和i分别用复数表示为=6（cos120°+jsin120°）≈（-3+j5.2）A

=8（cos30°+jsin30°）≈（6.9+j4）A

所以，I=+=（-3+j5.2+6.9+j4）A=（3.9+j9.2）A

=10（cos67°+jsin67°）A

最后将电流写成对应的解析式i=10sin（ωt+67°）A.

从例题中可以看出，用复数表示正弦型交流电可以简化解题过程。数学公式在电工中的应用数不胜数，这里就不一一列举了。

总之，数学在电工专业中的应用非常广泛，不管是在什么内容中，时时刻刻都有数学的影子。出于传统教学模式的弊端，如何发挥数学在电工专业中的应用，是当今职教类学校电工专业中数学教学的首要任务。一是可以提高学生对数学的学习兴趣，二是可以提高数学课堂教学效率，三是可以与专业课相辅相成，互相促进。数学任课老师可以根据教学需要适当地安排教材内容，按尺度适当删选、补充，以与专业课相结合为基础，广纳教材，精选精华，在数学应用方面下工夫，甚至于编写分别适合各个专业的校本教材。

参考文献：

[1]周绍敏.电工基础.

[2]陈其纯.电子线路.