经历图形认知过程 积累思维活动经验

宋健泳 范新林

数学是思维的科学，数学教学的重要任务之一就是要帮助学生积累思维经验、发展思维能力。这里所说的思维经验，主要是指思维活动中所获得的过程性体验。可见，思维经验的积累与学生在数学学习中的思维参与程度密切相关，思维介入越积极，所获得的体验也就越深刻。那么在具体的教学实践中，思维经验该如何体现？教师又应该如何帮助学生积累思维经验？笔者将结合“平面图形的认识”的教学作一些探讨。

“平面图形的认识”是“图形与几何”领域的重要内容。小学阶段认识的平面图形包括：线和角、三角形、四边形、圆和扇形等。一般来说，认识图形的特征需要经历的数学活动包括描绘、抽象、分类等。因此，在设计和开展这些数学活动时，教师应该具有明确的目标意识和过程意识，这是有效积累思维经验的前提。

一、在图形的描绘中提取思维的元素

思维的元素是指思维活动的基本构成单位，如概念、命题等。在图形认知的思维活动中，基本的思维元素是点、线、面、体，教师可以通过图形的描绘认识这些基础的几何概念。

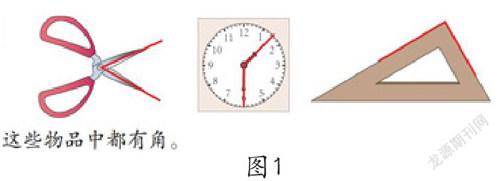
事实上人们对图形的抽象就是从描绘物体的外部形象开始的，也就是将三维空间的物体用线条描绘在二维平面。同样，小学生认识图形首先也要经历描绘图形的过程。教材中针对小学生的思维特点，一般将生活中的三维物体处理成图片的形式呈现（如图1，“角的初步认识”人教版二上第39页），从而简化了抽象的过程。

教材中的图片是静态呈现的，描绘图形则是一个动态的过程。这就需要教师在教学中改变图片的呈现方式，使学生借助观察、操作等实践活动经历从实物图片中描绘、勾勒数学图形的过程，从而积累思维经验。

图1

1.出示课本实物，找一找课本封面的角在哪里？学生大都指向角的顶点。

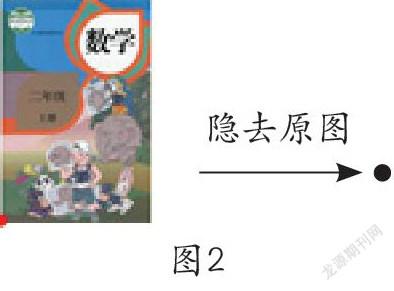
2.多媒体呈现课本图片，并动态演示（隐去原图，留下一个点，如图2）。请学生判断是不是角。

学生都认为这只是一个点，不是角。

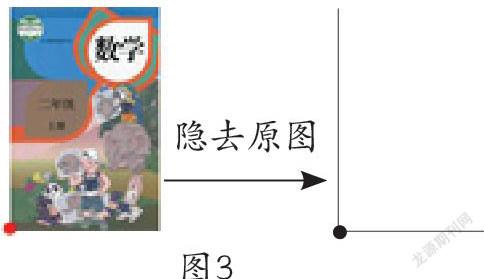
3.进一步思考，怎样画才能形成一个角？学生认为还要画上两条边（动态演示，图3）。

4.用水彩笔描出右面图中（图4）的角。

5.反馈后多媒体动态演示（图5）。

6.说一说数学中的角是什么样的。

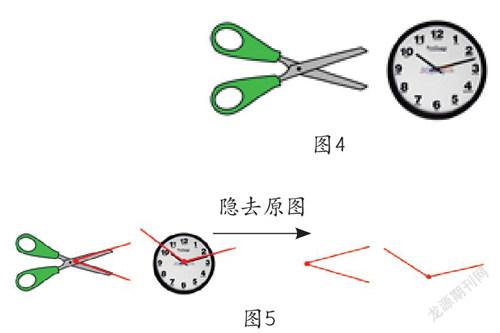
从上述教学活动中可以看到，尽管“点、线、面、体”这些概念非常抽象，学生却可以通过描绘和勾勒在自然而然的状态下提炼出来。可见，描绘对于图形的抽象是极其重要的，这是从生活到数学的抽象，因而是最直接、也是最本源的思维经验。除此以外，在教学活动中还拓宽了学生的思维视角。如一开始学生只关注局部，他们把物体“尖尖的部分”看成是角，这是源于生活中对桌角、墙角等的认识，与作为几何图形的“角”是不同的。但是，错误也是一种经验。在动态演示（舍去实物的图片背景）中，学生逐步认识到“尖尖的部分”只是一个点，只是“角”的一个部分。要完整地表示一个“角”，需要关注图形的整体，即还要在“点”的基础上辅上两条边。显然，这样的认识是直观的，也是深刻的。

二、在图形的抽象中实现思维的聚焦

经历图形的描绘过程使学生认识了平面图形的构造方式——点和线的组合。但要深入了解图形，还需要进一步抽象图形的基本特征。所谓抽象，就是“对同类事物抽取其共同的本质属性或特征，舍去其非本质的属性或特征的思维过程”。这个取舍的过程从思维的角度讲就是一个聚焦的过程。以“长方形和正方形的认识”的教学为例，过程如下：

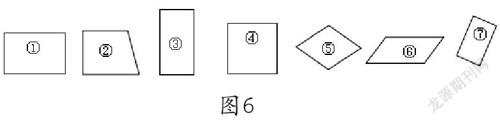
1.呈现用各种颜色彩纸剪成的四边形（图6），从中找出长方形。

图6

学生一致认为图①、图③和图⑦是长方形，对图④是不是长方形有争议，大多数同学认为它是正方形而不是长方形。

2.讨论：图①、图③和图⑦颜色不同、大小不同，为什么它们都是长方形？你们是怎么判断的？

讨论后学生的意见趋于一致，即两条标准：四个角都是直角、相对的边相等。

3.对图①、图③和图⑦进行操作验证（量一量、折一折）。

4.进一步讨论：图④是一个正方形，如果用长方形的标准去判断，它符合要求吗？

经过充分讨论和思辨，学生开始认可图④也是一个长方形。

5.思考：正方形是特殊的长方形，特殊在哪里？

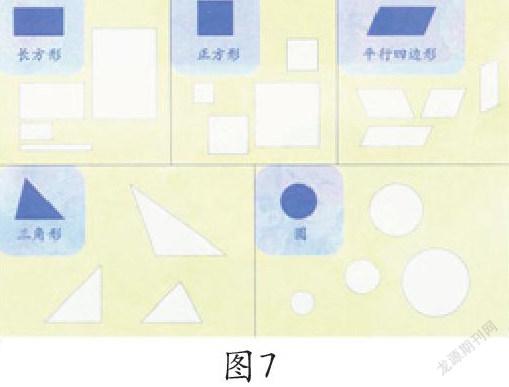
从本质上讲，图形的抽象就是舍去颜色、质地等物理属性，研究形状、大小、位置关系等数学属性。对于长方形和正方形，学生在一年级时已有了初步认识（图7）。这节课的教学任务是认识长方形和正方形的特征，其中难点在于理解和接受“正方形是特殊的长方形”这一具有从属关系的概念。为此，一方面教学中有意识地设置了一些干扰因素，如不同的颜色、不同的大小、摆放的角度，还包括长方形的形状也有所区别。这样设计的意图在于延长思维聚焦的体验过程，即摆脱一些非本质因素的影响，有选择地将思维关注点逐步聚焦于决定图形特征的两个要素：边和角。或者说，让学生充分理解只要符合对边相等、四个角都是直角的四边形，不管是什么颜色、多少大小、长的、扁的、正着放、斜着放都叫长方形;同样，判断一个四边形是不是正方形也只要看是不是符合四个直角、四边相等就可以了，与其他因素无关。另一方面，在这个过程中学生还学会了用一个确定的标准去进行判断，并以此认识了长方形和正方形之间的从属关系，突破了教学难点。判断是一种较高层次的思维形式，在这里也可以理解为是一种思维经验的具体体现。

三、在图形的分类中梳理思维的脉络

分类是认识事物的一种重要的方法。分类的基础是比较，在认识图形的教学中分类的过程就是通过比较不断寻找图形之间共性和差异的思维过程，也是对图形本质特征的认识不断深化的过程。如果从思维的角度看，分类活动包含了思维的起点、“拐”点、条理和层次等，我们称之为思维的“脉络”。如三角形的分类：

1.出示下图（图8），给图中的三角形分一分类。

图8

反馈：

方案一：图④、图⑦为一类;图①、图②、图③、图⑤、图⑥为一类;

理由：有直角的分一类，没有直角的分一类;

方案二：图④、图⑦为一类;图③、图⑥为一类;图①、图②、图⑤为一类;

理由：有直角的分一类;有钝角的分一类;都是锐角的分一类;

方案三：图②、图⑥、图⑦为一类;图①、图③、图④为一类;图⑤为一类;

理由：有两条边一样长的分一类;三条边都一样长的分一类。

2.比较这四种不同的分法，你有什么发现？

学生讨论后得出：前两种方案都是根据三角形的“角”来分类的，方案三则是根据“边”的长度来分类的。

3.揭示：如果按“角”分，一般分为三类：锐角三角形、直角三角形、钝角三角形。想一想，一个三角形会不会既是直角三角形又是锐角三角形？

生：有可能，因为直角三角形里也有锐角。

生：不可能。任何一个三角形里都有锐角的，锐角三角形必须三个都是锐角。所以直角三角形不可能是锐角三角形。

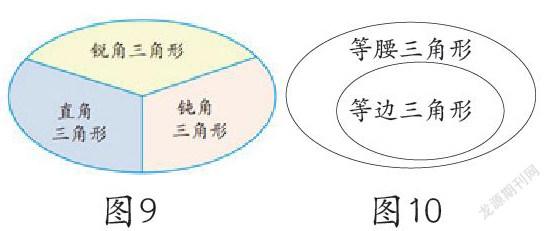
师：也就是说如果按“角”分类，那么一个三角形不可能同时具备两类不同的特征。这样的关系我们可以用一幅图来表示。（呈现图9）

4. 揭示：如果按“边”分，有两类特殊的三角形：等腰三角形、等边三角形。想一想，等边三角形是不是等腰三角形？

生：是的。只要两条边长度相等就是等腰三角形，等边三角形三条边的长度都相等，当然也是等腰三角形。

师：我们可以把等边三角形看作是特殊的等腰三角形。它们的关系也可以用怎样的图来表示呢？（呈现图10）

分类时首先要考虑的是确定分类的标准，这是思维的起点。对于平面图形来说，分类的主要标准是“边” 和“角”。其中，按“边”分类主要考虑的是条数、长度和位置关系（如对边是否平行）;按“角”分类则主要考虑直角，如有没有直角（本质上还是边的位置关系——邻边是否垂直）或者以直角为“分水岭”。这样的经验在前面的学习中学生其实已经有所感悟，因而在上述案例中可以看作是思维经验的运用。教学中要求学生陈述分类的理由，分享分类的经验，这是帮助学生体验思维逻辑性和条理性：思维的起点（分类的标准）不同，所得到的结论迥然相异。进一步，教师还要引导学生感悟思维的层次性，即按照这两种标准分类后，各类三角形相互之间的关系是不一样的。按角分类重点关注的是“差异性”，所分得的三类三角形是“互不兼容”的并列关系;按边分除了关注差异还要关注“共性”，如等边三角形既然三条边都相等，则必然其中有两条边相等，也就是具备了等腰三角形的特征，这是一种从属关系（包含关系）。这种思维经验的积累将为学生后继学习中研究图形之间的关系打下良好的基础。

综上，可以看到思维经验是一种基于主观的、富有感性特征的过程性体验。尽管它是一种隐性的数学素养，但在教学中帮助学生有效积累思维的经验也并非无迹可循。只要教师有意识地展开数学知识的发生过程，积极引导学生展开思维活动，那么思维层面的体验与感悟将不断丰富、不断积淀，最终会形成特有的数学思维方式，并逐步建立一定的数学直观。

（浙江省湖州市凤凰小学  313000

浙江省湖州市湖师附小教育集团  313000）