Banach空间中非局部二阶微分包含的可控性*

朱 琳，刘宏亮，于金凤

(哈尔滨师范大学)

0 引言

微分包含可控性问题已得到广泛的关注和研究，其中非局部问题于1991年，由Byszewski［1］做了较早的研究工作.2000年，Benchohra和Ntouyas［2］研究了具有非局部条件二阶微分包含在有限区间的可控性.2001年［3］将这一结果推广到无限区间的可控性.2006 年，Chang 和 Li［4］研究了二阶微分和积分包含的可控性.近年来，非局部可控性取得了很多研究成果.例如，2010年，于金凤等［5］研究了一类带有非局部条件二阶微分包含的可控性.2011年，张文超等［6］应用集值函数不动点定理来研究Banach空间中微分包含的近似可控性.

该文在Banach空间中讨论非局部二阶微分包含，形如:

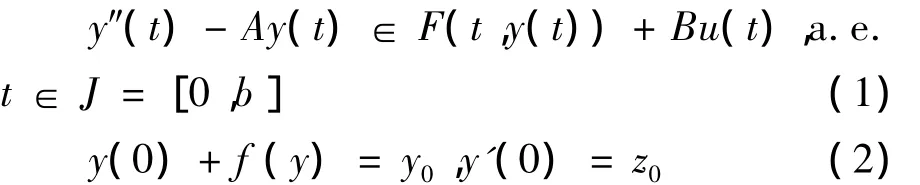
其中:E=(E，‖·‖)为一实Banach空间.

F:J×E→2E是有界闭凸集值映射.f:C(J，E)→E，y0，z0∈E·A是E上强连续余弦族{C(t):t∈R}的线性无穷小生成元.控制函数u(·)∈L2(J，U)，这里U是一个Banach空间，B是从U到E的有界线性算子.

1 预备知识

C(J，E)是从J到E上连续函数的全体，其范数为 ‖y‖∞=sup{|y(t)|:t∈J}，B(E)是从E到E的有界线性算子的Banach空间.L1(J，E)表示Bochner可积函数y:J→E的全体，其中表示在C(J，E)中0的邻域，Vp={y∈C(J，E):‖y‖∞≤p，p∈N}.

令(X，‖·‖)是一个Banach空间，集值映射G:X→2X，如果对任意的x∈X，G(x)是凸(闭)的，则称G是凸(闭)的.如果对任意的D⊂，是有界的，则称G是有界的，即

对于任意的x0∈X，G(x0)是X中的非空闭子集，且对任意开集V，G(x0)⊆V，存在x0的开邻域，使得G()⊆V，则称G是上半连续的.如果对有界子集D⊆X，G(D)是相对紧的，则称G是全连续的.如果G是全连续的，且有非空紧值，则G是上半连续的，当且仅当G有闭图像即

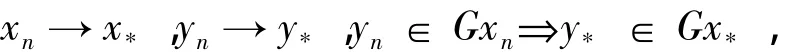
如果存在x∈X，使得x∈Gx，则称G有不动点.

BCC(X)表示X中所有非空有界闭凸子集的全体，设集值映G:J→BCC(X)，如果对任意的x∈X，d(x，G(x))是在J上的可测函数，则称G是可测的.对于任意的x∈X，通过

定义F的可积选择集.

如果满足:

①C(0)=I，其中I是在B(E)中的单位算子;

②对任意的s，t∈R，C(t+s)+C(t－s)=2C(t)C(s);

③对任意的y∈E，映射tC(t)y是强连续的.

则称Banach空间E上的算子族{C(t):t∈R}是强连续余弦算子族.

结合给定的强连续余弦算子族{C(t):t∈R}，定义

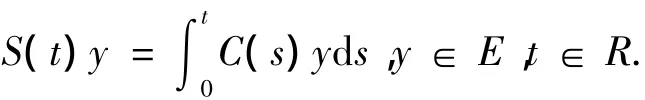
则称{S(t):t∈R}是强连续正弦算子族.

令A:E→E，定义为Ay=(d2/dt2)C(0)y，其中D(A)={y∈E，C(t)y是关于t的二次连续可微函数}，则称A为强连续余弦族{C(t):t∈R}的无穷小生成元.令Y={y∈E，C(t)y是关于t的一次连续可微函数}.

定义1 函数y∈C(J，E)，满足

且y(0)+f(y)=y0，y'(0)=z0，则y(·)称为是系统(1)－(2)的mild解.

定义2 系统(1)－(2)可控是指对任意的y0∈D(A)，z0∈Y，存在控制函数u∈L2(J，U)，满足y(b)+f(y)=y1∈D(A)，y'(b)=z1∈Y，其中y(·)是系统(1)－(2)的mild解.

为证明该文结果，需要作如下假设:

(H1)A是Banach空间E上强连续余弦族{C(t):t∈R}的线性无穷小生成元，存在常数M＞0，使得M=sup{‖C(t)‖:t∈J}.

(H2)F:J×E→BCC(E)，且F满足:对任意的y∈X，tF(t，y)，是可测的，对任意的t∈J，yF(t，y)是上半连续的;对固定的y∈C(J，E)，集合

SF，y={g∈L1(J，E):g(t)∈F(t，y(t))，a.e.t∈J}是非空的.

(H3)f是全连续的，存在L＞0，使得对任意的y∈E，‖f(y)‖ ≤L.

(H4)设线性算子W:L2(J，U)→E，定义为存在取值于L2(J，U)/kerW上的有界逆算子W－1，且存在M1，M2＞0，使得 ‖B‖ ≤M1.‖W－1‖ ≤M2.

(H5)设线性算子Wˉ:L2(J，U)→E，定义为存在取值于L2(J，U)/ker上的有界逆算子，且存在M3＞0，使得

(H6)存在M4＞0，使得 ‖A‖≤M4.

(H7)‖F(t，y)‖ =sup{‖ν‖∈F(t，y)}≤p(t)Ψ(‖y‖)}，t∈J，y∈E，其中p∈L1(J，R+)，Ψ:R+→(0，∞)是连续递增的，且

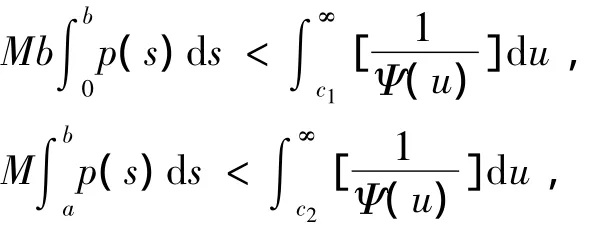
其中

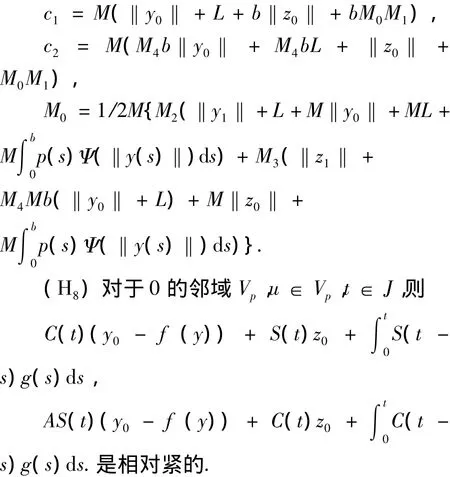
引理1［7］令X是Banach空间，I是紧的实区间，F是满足(H2)的集值映射，且Γ:L1(I，X)→C(I，X)是线性连续映射，则

Γ◦SF:C(I，X)→BCC(C(T，X))，y→(Γ◦SF)(y)=Γ(SF，y)是C(I，X)×C(I，X)上的闭图算子.

引理2［8］令X是局部凸空间，Q:X→2X是具有紧凸值的上半连续集值映射，使得对任意的0的闭邻域Vp，任意的p∈N，Q(Vp)是相对紧的.如果集合

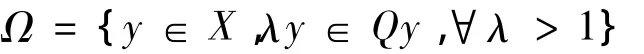
是有界的，则Q有不动点.

2 主要结论

定理1 若假设(H1)－(H8)成立，则系统(1)－(2)是可控的.

证明 由(H4)和(H5)，对任意的y(·)∈(J，E)，定义控制函数

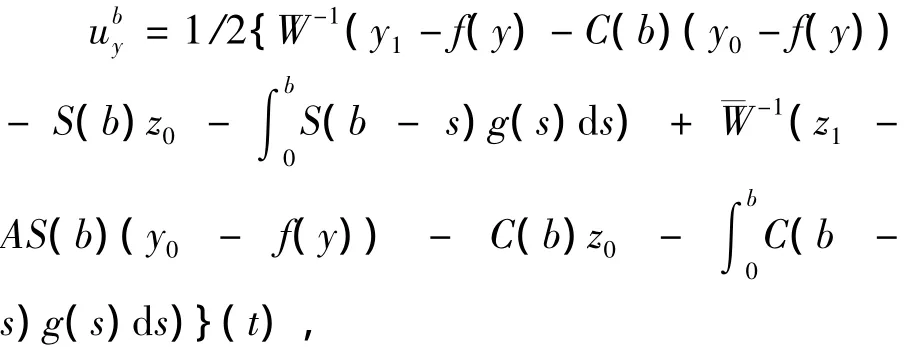
其中

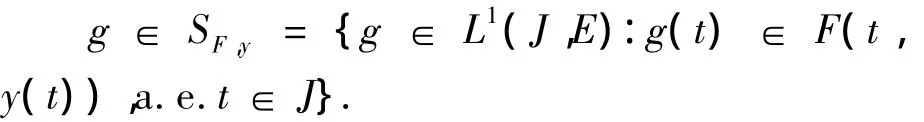
利用控制函数定义集值映射Q1(·):C1(J，E)→ 2C1(J，E)，Q2(·):C(J，E)→ 2C(J，E)，具有如下形式:

证明集值映射Q1(·)，Q2(·)有不动点，y1－f(y)∈(Q1(y)(b)，z1∈(Q2y')(b)分以下几步进行证明.

第一步:对于任意的y∈C1(J，E)，y'∈C(J，E)，Q1y，Q2y'是凸的.

设h1，h2∈Q1y，则存在g1，g2∈SF，y，使得对任意的t∈J，有

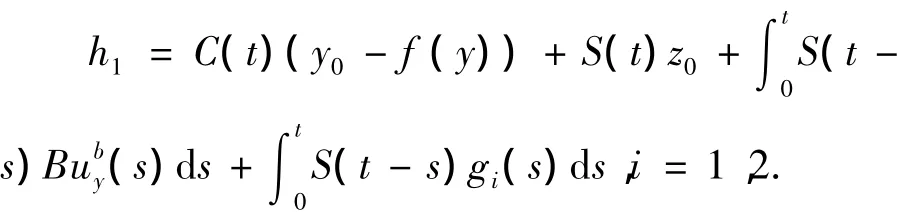
令0 ≤α≤1，则存在g1，g2∈SF，y，使得对任意的t∈J，有

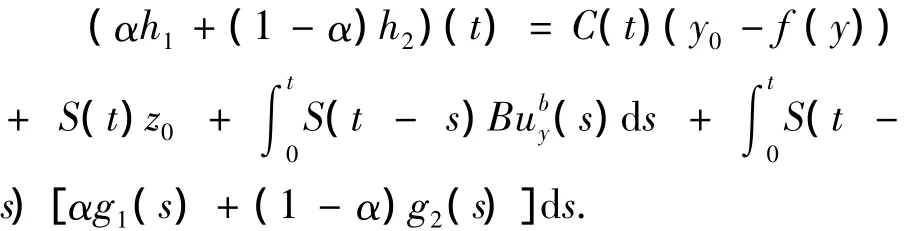
因为F有凸值，所以SF，y是凸的，则αh1+(1－α)h2∈Q1y.同理，Q2y'是凸的.

第二步:对于任意的q1∈N，q∈N，Vq1∈C1(J，E)，Vq∈C(J，E)，Q(Vq1)和Q(Vq)是有界的.

要证存在一个正数l1＞0，使得对每个h∈Q1y，y∈Vq1，有 ‖h‖∞≤l1，若h∈Q1y，则存在g∈SF，y使得

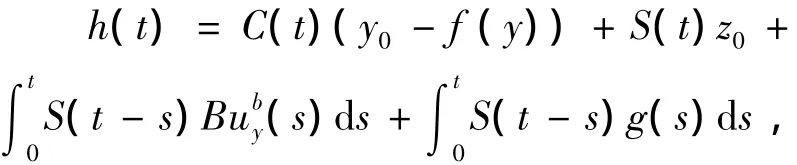
通过假设(H1)和(H3)～(H7)，对于任意的t∈J，有

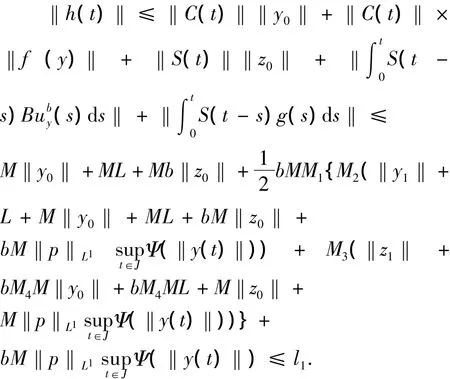
同理，‖h'(t)‖≤l2.

第三步:对于任意的q1∈N，q∈N，Vq1∈C1(J，E)，Vq∈C(J，E)，Q(Vq1)和Q(Vq)是等度连续的.

设t1，t2∈J，t1＜t2对任意的y∈Vq1，h∈Q1y，存在g∈SF，y，使得

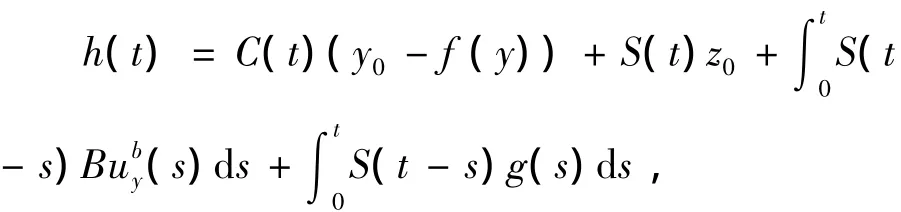
因此，

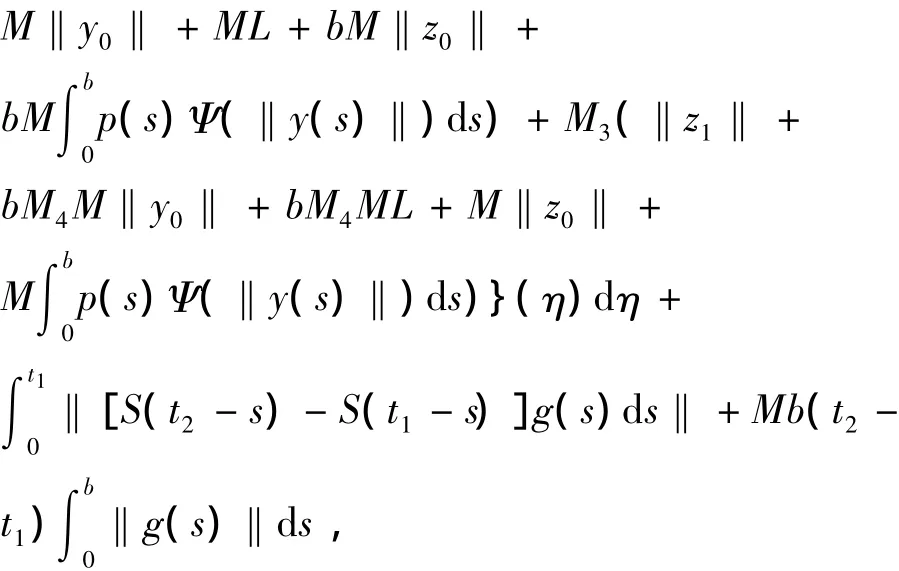
当t2→t1时，上述不等式右端趋于零，故Q(Vq1)是等度连续的.同理，Q(Vq)是等度连续的.由步骤二，三，(H3)，(H8)知，Q1(·)，Q2(·)是全连续的.

第四步:集值映射Q1(·)，Q2(·)是上半连续的，只需证Q1(·)，Q2(·)有闭图像.

令yn→y*，hn∈Q1yn，hn→h*，要证h*∈Q1y*.由hn∈Q1yn，hn'∈Q1yn'，则存在gn∈SF，y使得

其中

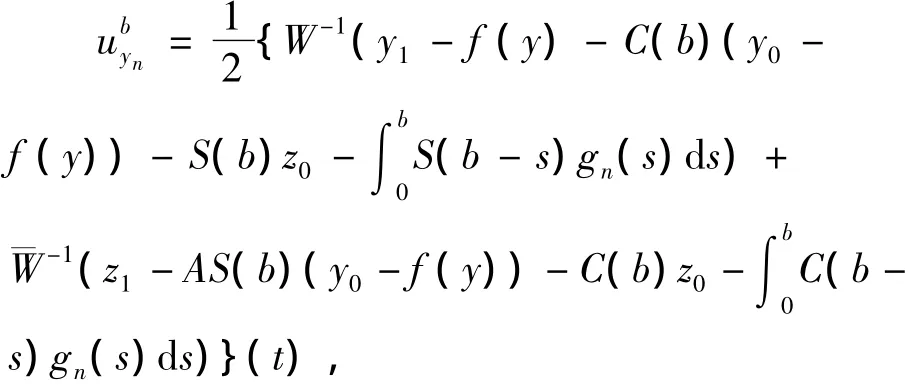
要证，存在g*∈SF，y*，使得

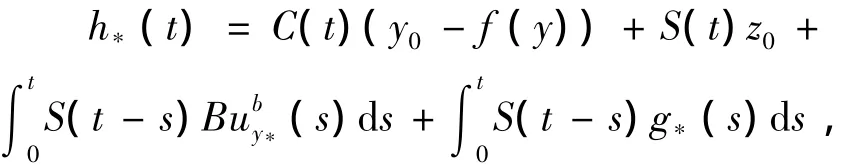
令

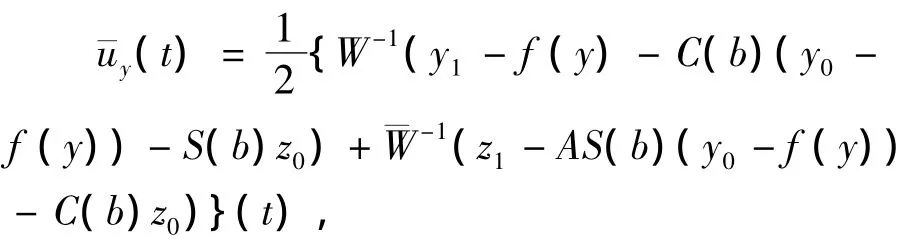
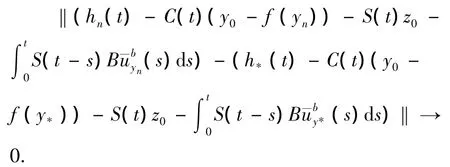
现在考虑线性算子Γ1:L1(J，E)→C(J，E)

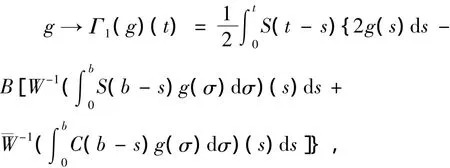
并且

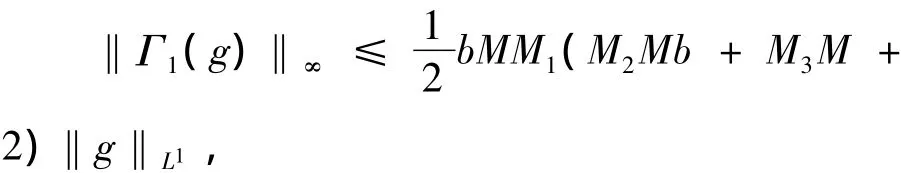
显然Γ1是线性的，故Γ1是连续的.由引理1，Γ1◦SF，y有闭图像，并且有

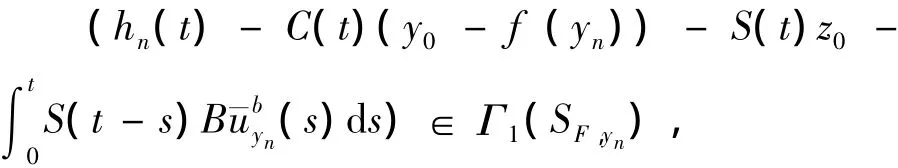
因为yn→y*，所以存在g*∈SF，y有

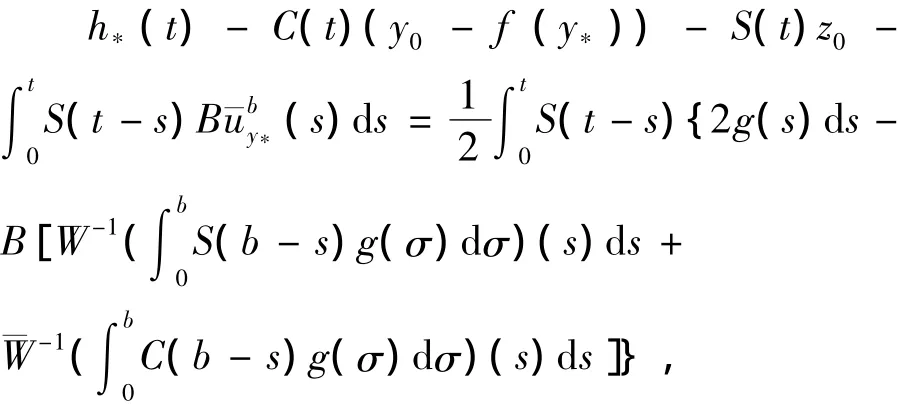
因此，Q1(·)有闭图像.同理，Q2(·)有闭图像.

第五步:证明集合

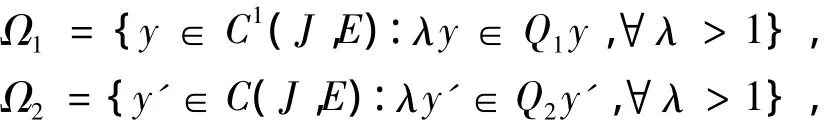
有界的.

因此，存在g∈SF，x，使得

故有

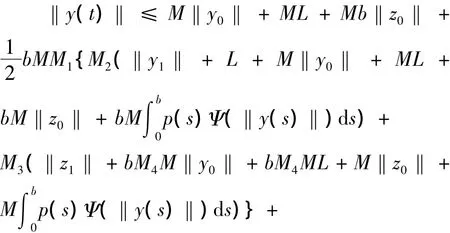
右端式子记为v(t)，则有

由于Ψ是非降的，有

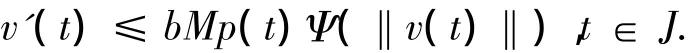
因此，对于任意的t∈J，有

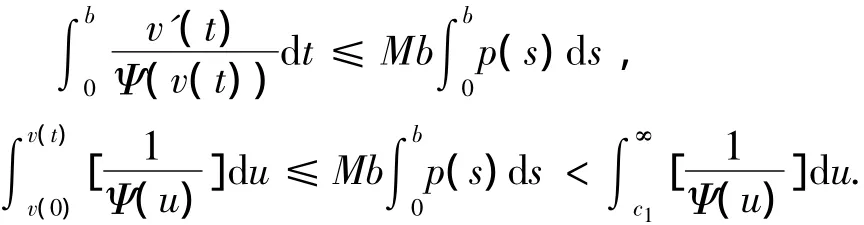
故存在常数d，使得

因此‖y‖≤d.

故Ω1有界.同理，Ω2有界.

由引理2知，Q1，Q2有不动点，因此系统(1)－(2)是可控的.

［1］Byszewski L.Theorems about the existence and uniqueness of solutions of a semilinear evolution nonlocal cauchy problem，［J］.Math Aral Appl，1991，162:494–505.

［2］Benchohra M，Ntouyas S K，Controllability of second－order differential inclusions in Banach spaces with nonlocal conditions［J］.Optim Theory Appl，2000，107:559–571.

［3］Benchohra M，Ntouyas S K，Controllability for an infinitetime horizon of second－order differential inclusions in Banach spaces with nonlocal conditions［J］.Optim Theory Appl，2001，109:85－98.

［4］Chang Y K，Li W T.Controllability of second－order differential and integrodifferential inclusions in Banach spaces［J］.Optim Theory Appl，2006，129:77–87.

［5］于金凤，陈安妮.带有非局部条件二阶微分包含的可控性［J］.数学学报，2010，53:871–880.

［6］张文超，于金凤，马吉溥.Banach空间中立形微分包含的近似可控性［J］.哈尔滨师范大学自然科学学报，2011，27:24－28.

［7］Lasota A，Opial Z.An application of the Kakutani－Ky－Fan theorem in the theory of ordinary differential equations［J］.Bull Acad Polon Sci，1965，13:781–786.

［8］Ma T W.Topological degrees for set－valued compact vector fields in locally convex spaces［J］.Diss Math，1972，92:1–43.