一类微气泡耦合时滞系统的稳定性以及Hopf分支*

王进斌，蒋卫华

(1.太原科技大学;2.哈尔滨工业大学)

0 引言

Rayleigh［1］是最早分析气泡系统的，他的工作主要是考虑处在常值外压下的不可压缩液体中的气泡模型.Gilmore，Plesset和 Prosperetti［2－3］等研究的气泡微分方程模型是处在可压缩的液体中，并且液体背景外压的变化依赖于时间.他们研究的模型就是著名的 Rayleigh－Plesset方程，方程中球型气泡的动力学行为完全被气泡的半径所刻画:

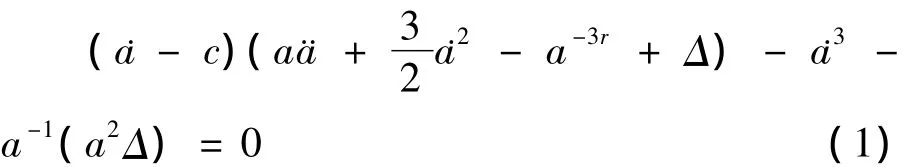
其中Δ =ρ-1(p(a)-p0)，p是液体的密度，p(a)是气泡内部的压强，是气体的绝热指数，k用来描述气泡中气体的数量，p0是指液体无穷远点处的压强.

对(1)进行无量纲化，得到

方程(2)仅考虑了液体中有一个球型气泡的情形.若液体中有大量气泡侵入，这种状况由于气泡间压力波的存在，使得气泡相互耦合.对于微气泡时滞耦合系统的研究，人们更关心气泡间的耦合同步现象.目前，Heckman C R和Rand R G［4］研究的气泡耦合振子系统为:

他们对系统(3)在完全同步(a=b，˙a=˙b)的情形下，系统(3)变为:

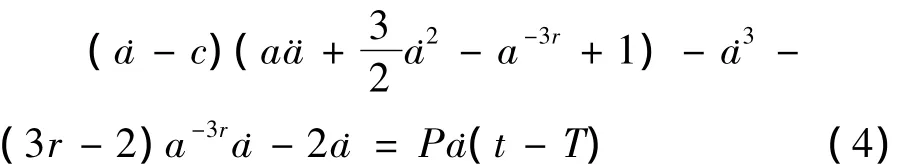
作者仅在时滞T∈［0，T0］下，对系统(4)在平衡点附近的局部稳定性做了讨论.然而，在时滞T大范围变化时，系统平衡点处的稳定性和Hopf分支变化情况作者没有作深入的研究.该文将主要对微气泡耦合时滞系统(4)在时滞T大范围变化时的局部稳定性和Hopf分支作出研究.这里参数c，r，P是以系统(2)中被定义的，其中c表示声速，r表示该液体的比热比，P表示系统的耦合强度.

1 平衡点的稳定性定性分析及Hopf分支存在性

对于系统(3)，可以解得平衡点(ae，be)=(1，1).

把(5)代入(4)式得

方程(6)对应的特征方程为:

下面将对方程(7)根的分布进行定性分析:

①当T=0时，方程(7)化为二次方程为:

解得其根为

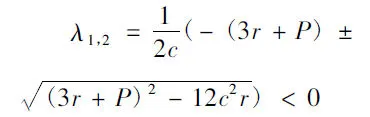
②当T≠0时，假设iω(ω＞0)是特征方程(7)的解，代入分离实虚部得:

将该二式的两端平方相加得到

为了方便，记

其中A=c2，B=9r2－6c2r-P2，E=9r2c2，t=ω2.

解得，当P＞3r时

则有

引理1.1 当P＞3r时，

证明 由(10)可得出

于是有

而

则

即有

当P＞3r时，

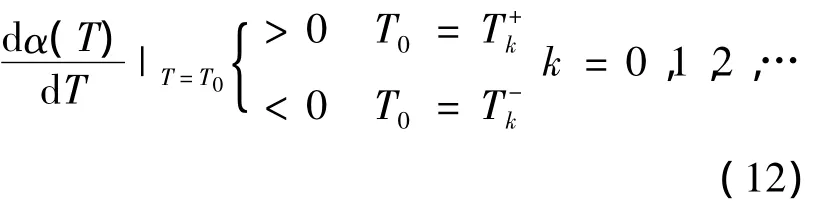
利用Wei和Ruan在文献［4］中的结论和引理1.1，进而得出如下结论:引理1.2当P＞3r成立时

① 当T∈［0，T0+］∪时，方程(8)的所有根的实部都是严格负的.

③当T取和Tk-时，方程(8)有一对简单的纯虚根.

定理1.1 当P＞3r成立时

2 模型物理现象的分析

流体中气泡的受力状况和运动规律是气泡动力学研究的主要内容.早期对气泡的研究是在假设流体体积在不可压缩的情况下，去讨论流体中球体微气泡的产生和消失现象，研究常常采用著名的Rayleigh－Plesset方程.

在上一节中，得出系统(4)在平衡点处在时滞T变化时会出现不同的状态.时滞T在前文的分析中有如下表达式:

在固定声速大小的情况下，两气泡之间的距离是与时滞T成正比的，而系统(4)零平衡点在时滞T超过某一临界值时都是不稳定的，并且系统的同步行为完全被破坏而产生混沌现象.即说明此时系统的耦合强度很小，而使得液体中的气泡处在无序的状态中.从图1时滞T与耦合强度P之间的关系中可看出:时滞T是随着耦合强度P的增大而减少的，即可说明T越大反而使得P变得越少.综上所述可得出，系统中气泡之间的耦合强度P是随着气泡之间的距离增大而减少的.这一结果与测试液体中气泡动力学性质的物理实验的结论是一致的.

图1 当c=94，r=3/4时，T与P之间的变化关系图

当耦合强度P→0时，系统(4)

中气泡之间的相互影响趋近于零.系统由两气泡的同步耦合变为单气泡振子的系统(2)

在前文的研究中得出，系统(2)平衡点都是局部稳定的.这也说明单气泡振子系统在缺少耦合强度的影响下能保持较好的动力学性质，然而，在液体环境中由于气泡的分裂与聚并，单气泡振子这一情形不常出现.因此，对双气泡振子系统的研究(4)能更好的接近气泡模型本身.

3 结束语

该文分析了微气泡耦合时滞系统的动力学性质.利用泛函微分方程的基本理论，对微气泡系统平衡点的稳定性进行了分析并给出Hopf分支产生的条件.此外，从数学的角度分析并得到液体环境中气泡之间的耦合强度P随着气泡之间的距离增大而减少这一实验结论.然而，关于系统的局部Hopf分支定性分析和分支性质是否可以进行全局延拓，系统产生双Hopf分支的条件将会是哪些?诸如此类问题尚有待于进一步分析和研究.

［1］Rayleigh L.On the pressure developed in a liquid during the collapse of a spherical cavity［J］.Philosophical Magazine Series，1917，34:94–112.

［2］Plesset M S.The dynamics of cavitation bubbles［J］.Applied Mechanics，1949，16:277–282.

［3］Plesset M S，Prosperetti A.Bubble dynamics and cavitation［J］.Annual review of fluid mechanics，1977，9:145–185.

［4］Ruan S，Wei J.On the zeros of transcendental functions with applications to stability of delay differential equations with two delays［J］.Dynamics of Continuous，Discrete and Impulsive Systems Series A:Mathematical Analysis，2003，10:863–874.