期权类衍生金融工具的多期二项式定价数学模型*
2015-09-09凌春英
凌春英
(黑龙江财经学院)
0 引言
期权是买方向卖方支付一定数额的期权费后获得的一种选择权,即买方拥有在一定时间内以一定的价格出售或购买一定数量的标的物的权利[1].二项式定价模型是给期权类衍生工具定价的基本方法,它已经成为建立复杂期权定价模型的基本手段.
1 模型假设
(1)市场没有摩擦,市场是竞争性的.
(2)市场参与者没有对手风险,认为财富越多越好.
(3)不存在无风险套利机会.
(4)允许使用全部所得卖空衍生证券.
(5)无风险利率r为常数,且对所有到期日都相同.
2 符号说明
S—标的资产的现货价格;
C—看涨期权的期初价值;
K—执行价格;
B—投资到无风险资产上的资金数量;
r—无风险利率;
n—买进现货的数量;
u—期货价格上升率,u>1;
d—期货价格下降率,d<1;
p—价格上升的概率.
3 单期模型
将期权的有效期分为2个时间段,如从0期到1期[2].标的资产现货价格从初始值S分别以p和1-p随机移动到两个新值Su和Sd中的某一个,则从S到Su是价格上升运动,而从S到Sd是价格下降运动.在1期,看涨期权的价值分别为Cu和Cd两种(如图1),则


图1
构造一个与看涨期权的收益相同的投资组合[3].买m单位现货并借款投资B到无风险资产上,则在0期投资组合的价值为

若到1期标的资产市价为Su,则投资组合的收益也应为Cu,即
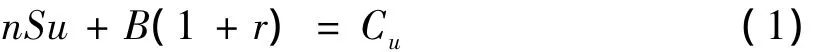
若到1期标的资产市价为Sd,则投资组合的收益也应为Cd,即
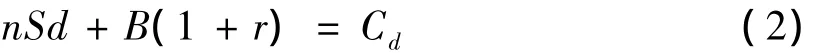
由(1)式和(2)式,可得

则求得相应的0期期权定价公式为

4 多期模型
从单期模型拓展到多期模型时,需要将标的资产价格变动的期限分割为两个或两个以上的期限[4].下面以两个时间期限为例,推导出两个时间间隔的期权定价公式.
将期权的有效期分为3个时间段,如从0期到2期,如图2.

图2
①标的资产现货价格从初始值Su分别以p和1-p随机移动到两个新值Suu和Sud中的某一个,若到2期标的资产市价为Suu,则投资组合的收益也应为Cuu,即

若到2期标的资产市价为Sud,则投资组合的收益也应为Cud,即

由(3)式和(4)式,可得

则求得相应的1期期权定价公式为

②标的资产现货价格从初始值Sd分别以p和1-p随机移动到两个新值Sdu和Sdd中的某一个,若到2期标的资产市价为Sdu,则投资组合的收益也应为Cdu,即

若到2期标的资产市价为Sdd,则投资组合的收益也应为Cdd,即

由(6)式和(7)式,可得

则求得相应的1期期权定价公式为

由(5)式和(8)式可得相应的0期期权定价公式为

5 案例应用
假设标的资产为不付红利股票,当前市场价格为100元,波动率为每年30%,无风险年利率为8%.该股票2个月期的看跌期权协议价格为100元.求该期权的价值.
为了构造二叉树,把期权有效期分为二段,每段一个月(等于0.0833年).则可以算出

由(9)式,可得该期权的价值为
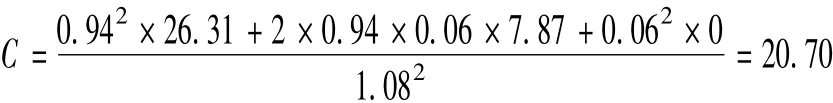
[1]叶永刚.衍生金融工具[M].北京:中国金融出版社,2004.
[2]孟生旺.金融数学:第三版[M].北京:中国人民大学出版社,2011.
[3]郑振龙,陈蓉.金融工程:第三版[M].北京:高等教育出版社,2012.
[4]孟生旺,袁卫.利息理论及其应用[M].北京:中国人民大学出版社,2001.
