用广义Y-切上图导数刻画集值优化ε-Henig真有效元
2021-01-21谢雪军
谢雪军,余 丽
(宜春学院 数学与计算机科学学院,江西 宜春 336000)
近年来,在线性空间中研究集值优化问题的最优性条件取得了一定的成果[1-3]。另一方面,由于集值优化理论逼近解与Ekeland变分原理之间有着密切联系,因此各种逼近有效解的概念被相继引入,文[3]在实序线性空间中引入了ε-Henig真有效解的概念,并得到了集值优化问题在ε-Henig真有效意义下的标量化定理。
本文借助广义Y-切上图导数的概念,在α-阶近似锥-弧连通集值映射假设下,讨论集值优化问题ε-Henig真有效元的充分和必要最优性条件。
1 基本概念
设X和Y为实序线性空间,M为Y的任一非空子集,以clM、intM和coneM分别表示M的闭包、内部和生成锥,其中,coneM={λm:λ≥0,m∈M}。M称为是锥,如果αm∈M,∀m∈M,α≥0。锥M称为是凸的,如果M+M⊂{M}。M称为是点的,如果M∩(-M)=0。C为Y中非平凡的闭凸点锥。设F:X→2Y是集值映射,则F的域,图和上图分别记为domF,graphF和epiF。
以下设V⊆Y是均衡吸收的凸集,满足0∉B+V。记CV(B):=cone(B+V)。
定义1.1[4]集合S⊂X称为弧连通集,如果对于任意的x∈S,z∈S,存在一连续向量值函数Hx,z:[0,1]→S,Hx,z称为弧,使得
Hx,z(0)=x,Hx,z(1)=z。
如果
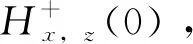
定义1.2[5]设S⊂X是一个非空弧连通集,F:S→2Y为集值映射。称F为α-阶近似C-弧连通集值映射,如果∃θ∈intC,α>0,对每个x∈S,z∈S,存在一个弧Hx,z:[0,1]→S,使得
t1+αθ+(1-t)F(x)+tF(z)⊂F(Hx,z(t))+C,0t1。
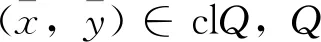
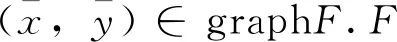
∀x∈X。
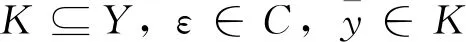
2 最优性条件
考虑下面的集值优化问题
(P)minF(x)
s.t.x∈S,
其中S是X的非空子集,F:X→2Y是集值映射。
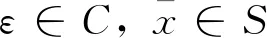
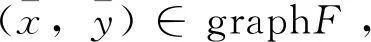
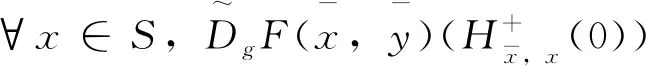
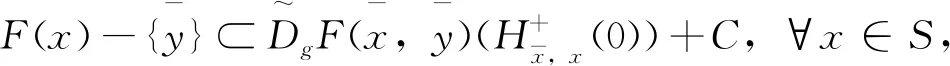
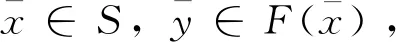
(1)
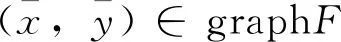
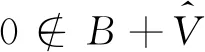
(2)
0∉B+V,有
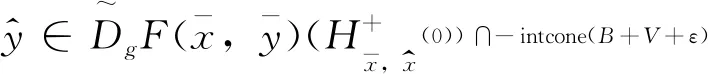
(3)
由广义Y-切上图导数的定义得
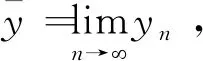
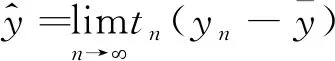
(4)
由(3),(4)式得∃n0∈N,使得
由-intcone(B+V+ε)是锥得
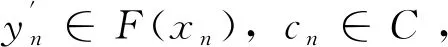
从而
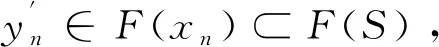
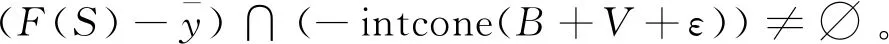
由文献[7]的定理2.1可知
此与(2)式矛盾,故定理得证。
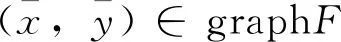
证 由(1)式及cone(B+V0+ε)是点凸锥知
由引理2.1,有
于是
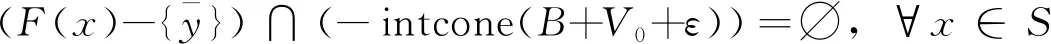
(6)
易证

(7)
于是有
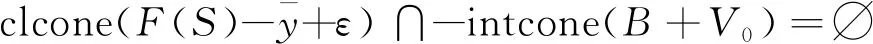
(8)
由凸集分离定理知存在0≠f∈Y*,使
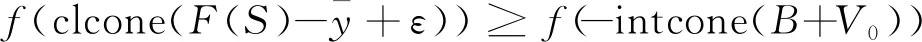
(9)
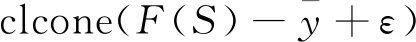

即
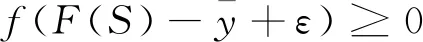
(10)
由V0=-V0及f(-intcone(B+V0))0,得
f(B)≥f(V0)。
于是
f∈Bst=C+i
(11)
