挤压式磁流变减振器力学模型研究

姚 军，张进秋，贾进峰，刘义乐（装甲兵工程学院装备试用与培训大队，北京100072）

挤压式磁流变减振器力学模型研究

姚 军，张进秋，贾进峰，刘义乐
（装甲兵工程学院装备试用与培训大队，北京100072）

为了克服剪切阀式磁流变减振器阻尼力最大值不够的缺陷，建立了挤压式磁流变减振器的数学模型，得出了挤压式磁流变减振器的阻尼力表达式，并定义了等效阻尼系数和可调倍数.根据理论推导的表达式，分析了磁流变液在平行圆盘间的流动特性以及影响阻尼力的因素.分析结果从理论上证明挤压式磁流变减振器是小位移大阻尼减振器，位移3mm情况下，最大阻尼力和可调倍数分别可达5000N和9.7947.

减振器；挤压流动；阻尼力；等效阻尼系数；可调倍数

按照磁流变液的工作模式，磁流变减振器可分为剪切式、阀式和挤压式3种.剪切式磁流变减振器磁路设计简单，但产生的阻尼力小；阀式磁流变阻尼器产生的阻尼力大，但磁路设计复杂.因而常见的磁流变减振器为这两种模式的复合形式，即剪切阀式磁流变减振器，它产生的阻尼力相对较大，磁路设计也相对简单.但该类减振器产生的阻尼力有限，不能满足重负荷减振需求，而挤压式磁流变减振器恰好具有产生大阻尼力的特性.

对于挤压式磁流变减振器力学模型的研究相对较少.闵峰［1］以实验方法测试了磁流变脂阻尼器的示功特性，定性找出了阻尼力与位移的关系及示功特性的变化规律.刘勇等［2］设计了一种小位移大阻尼的磁流变减振器，并进行了测试，但该研究集中于磁路设计，并没有提出力学模型.路国平等［3］和廖荣昌等［4］理论分析了挤压式磁流变减振器的力学特性，具有很强的指导意义，但没有考虑中间轴对减振器阻尼力的影响.郭朝阳［5］和章新杰［6］建立了挤压式磁流变减振器的力学模型，但公式复杂，不利于实际计算，所采用的经验公式存在误差.本文对挤压式磁流变减振器的力学模型作了进一步优化，以提高模型的准确性.

1　建立力学模型

1.1磁流变液本构方程

磁流变液在无外加磁场时，表现为牛顿流体状态；在外加磁场下，呈B i n g h a m流体，且随着场强的增大，磁流变液的剪切屈服强度提高.为了准确描述磁流变液上述两种状态，本文引入磁流变液的双黏度模型，即：

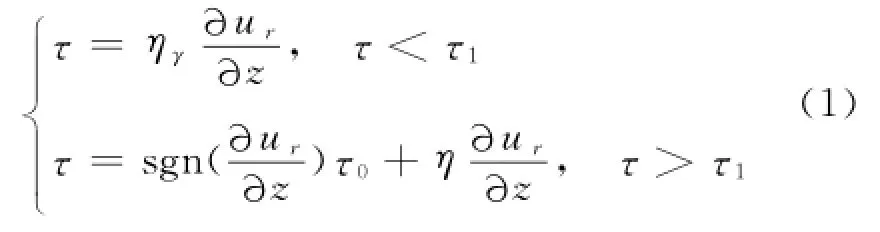
式中：磁流变液未屈服流动时的黏度是ηγ，磁流变液屈服流动时的黏度是η；τ0为静态屈服应力；τ1为动态剪切应力为磁流变液剪切

应变率.

ηγ，η，τ0和τ1应满足如图1所示的关系.

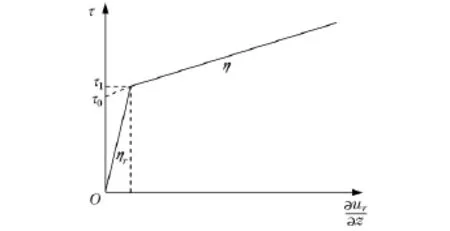
图1　磁流变液双黏度模型Fig.1 Double viscosity model ofmagnetoreological fluid

1.2圆盘式磁流变液挤压模型

由于圆盘间的磁流变液流动速度低，圆盘间隙小，假设磁流变液是不可压缩流体，可认为磁流变液在圆盘间的流动是定常流动.以圆盘间隙中心为原点O，半径方向为横轴r，圆盘垂直中心线为纵轴z，建立柱坐标系，如图2所示.圆盘间隙为2h0，半径为R，中间轴半径为r0，圆盘挤压速度为u0.

根据磁流变液的双黏度模型，圆盘间可分为2个区，中间部分剪切应力大于τ1，磁流变液屈服流动；靠近极板的磁流变液剪切应力小于τ1，未发生屈服；2个区域分界面上的磁流变液剪切应力等于τ1，分界面与上下圆盘的交点为R0.

1.3Navier边界条件

考虑到磁流变液壁面滑移效应，本文引入润滑理论的Navier边界条件.

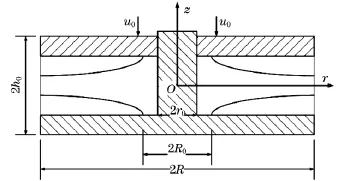
图2　圆盘挤压示意图Fig.2 Sketch map of squeeze flow

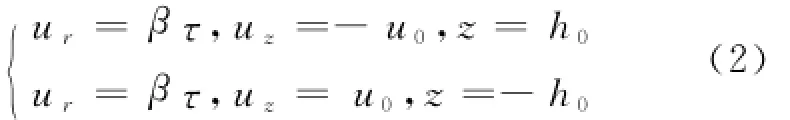
式中：β为滑移系数，β=0表示流体无滑移，β→∞表示流体充分润滑.研究表明，磁流变液在壁面存在滑移效应，但随着磁场的增强以及壁面材料选用高磁导率的材料，可认为磁流变液不存在壁面滑移效应，即β=0.

2　挤压流动分析

2.1径向速度和压力梯度分布

由于平行圆盘间的磁流变液可近似看成小雷诺数的蠕流问题，则Navier-S t Oc k s方程可近似为：

在r＞R0区域，对式（3）沿z轴积分，同时，z=0时，剪切应力τ=0，可得：

在屈服面上，τ=τ1，可得：

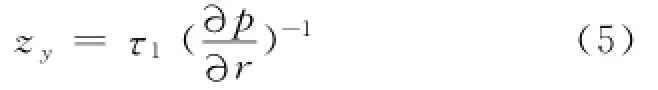
其中，zy是屈服分界面在z轴上的投影.在屈服区，将式（1）代入式（4）得：

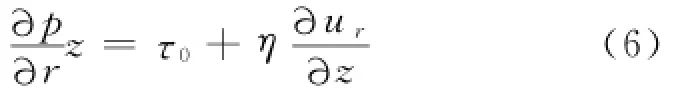
沿z轴积分得：由Navier边界条件，ur=βτ，z=-h0，得：

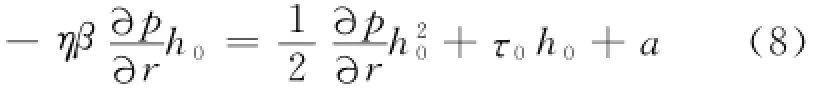
从而：

将式（9）代入式（7）得：

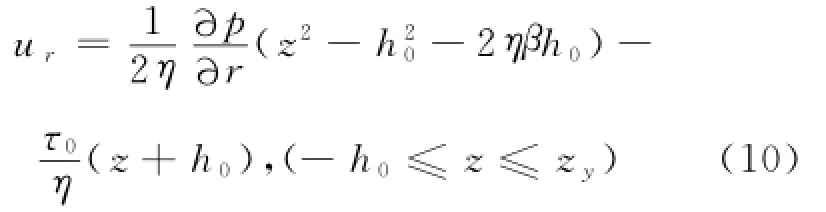
在未屈服区，将式（1）代入式（3）得：

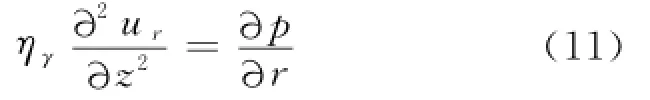
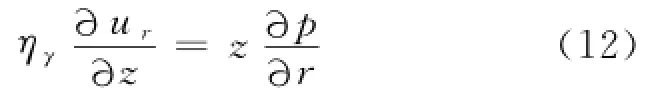
将式（12）沿z轴积分，得：

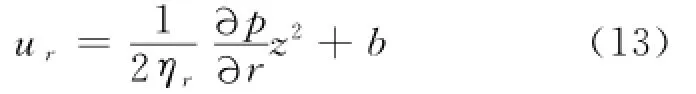
因为屈服面上速度连续，即式（10）和式（13）相等，得：

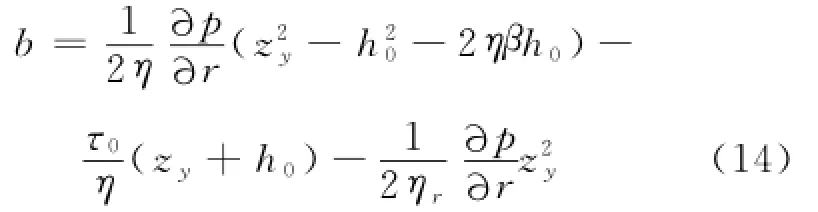
将式（14）代入式（13）得：

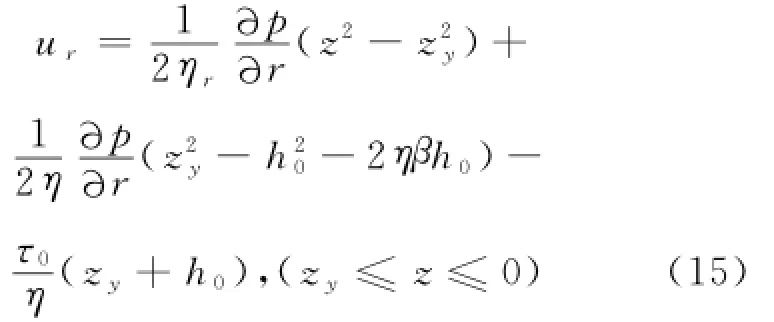
所以r＞R0区域内的速度分布为：

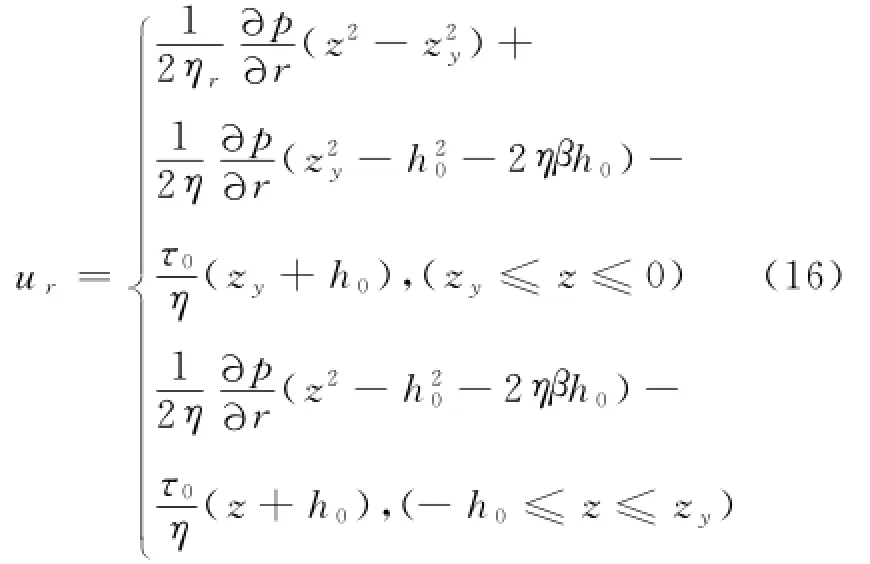
流体在圆盘间的流动满足质量守恒定律，由雷诺运输方程得：

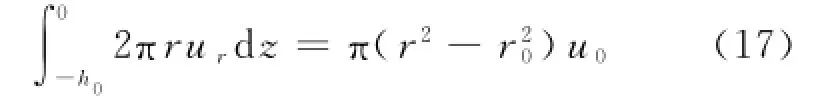
将式（16）代入式（17）得：

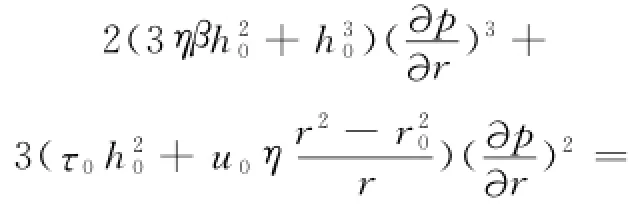
该方程为压力梯度的三次隐式方程，可以近似为压力梯度和半径的线性关系［7］，即：

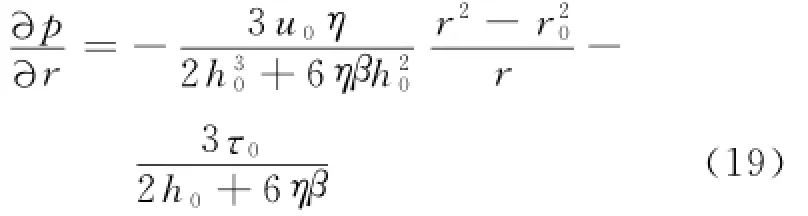
在r＜R0区域内，由式（17）变换可得：

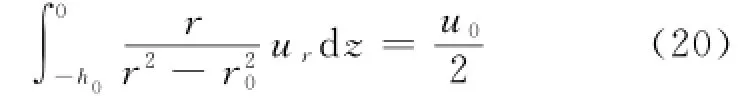
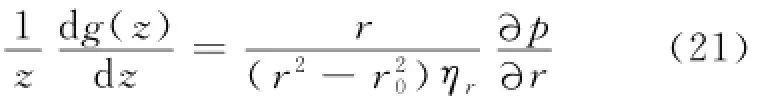
上述等式两边为z和r的函数，设等式等于常数a，则：

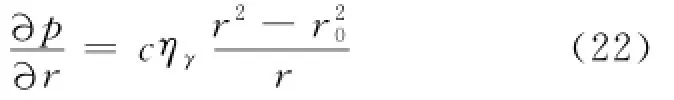
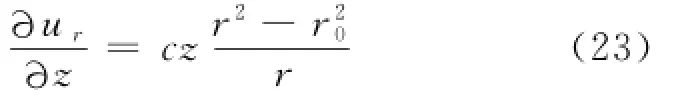
对式（23）沿z轴积分得：

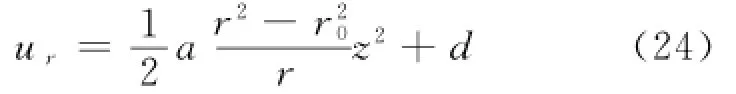
根据Navier边界条件ur=βτ，uz=u0，z=-h0，代入式（24）得：

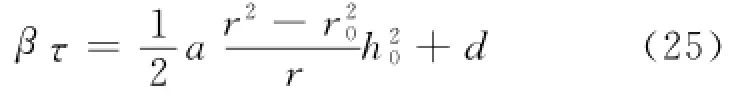
由式（1），（23），（25）以及边界条件得：

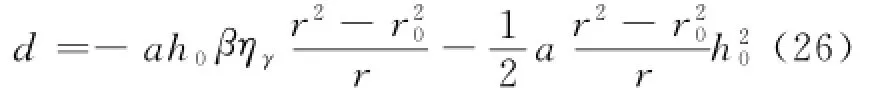
将式（26）代入式（24）得：

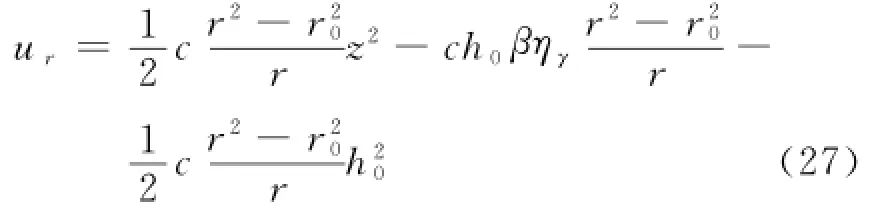
将式（27）代入式（20）得：

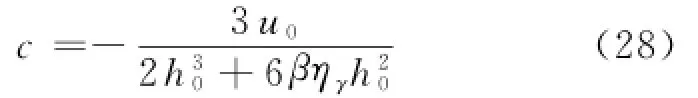
将式（28）代入式（27）得：

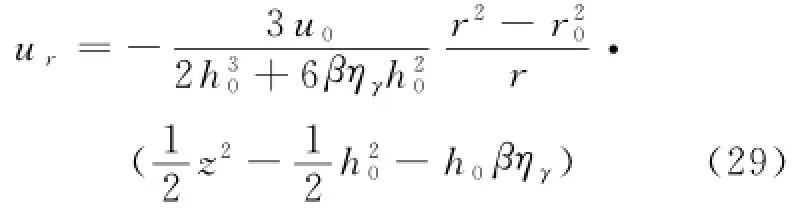
将式（28）代入式（22）得：

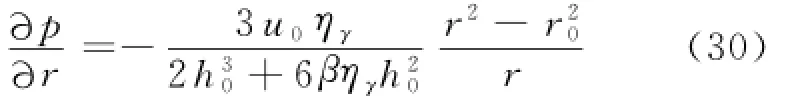
将式（30）代入式（3），并沿z轴积分得：

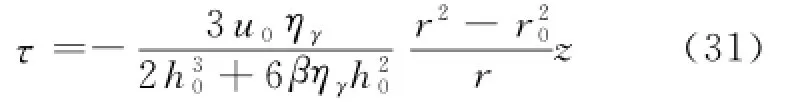
当r=R0时，τ=τ1，z=-h0，代入式（31），经过变换成二次方程，有2个实根，但只有其中1根符合要求，即：

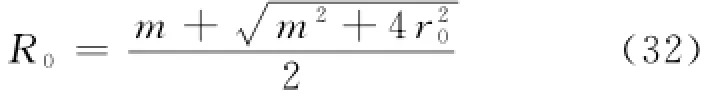
挤压式磁流变减振器的阻尼力F可用如下关系式计算得出：

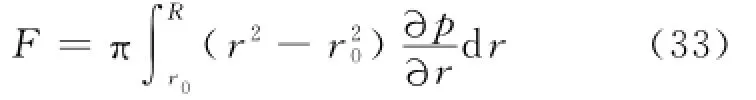
将式（19），（30）代入式（33），得到挤压式减振器的阻尼力为：

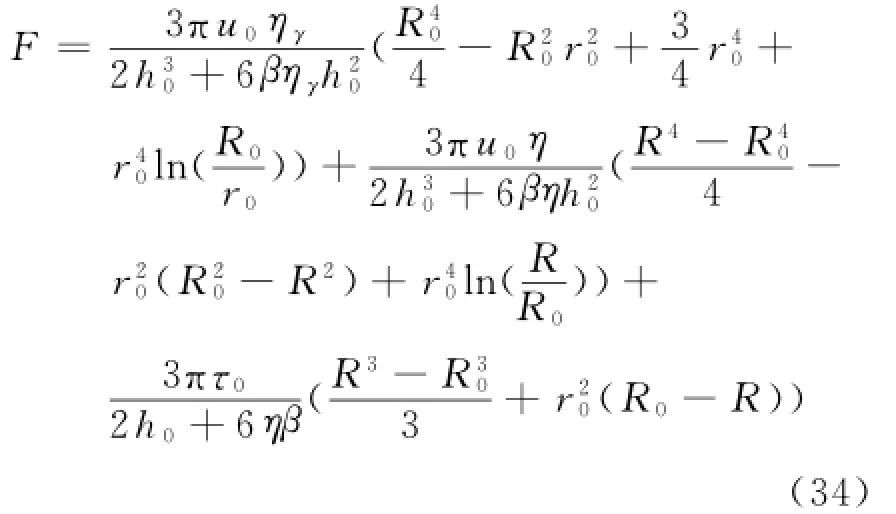
2.3可调倍数

可调倍数反映了变阻尼减振器的性能，是评价这类减振器好坏的重要指标.为了准确描述挤压式磁流变减振器的阻尼可调性能，本文进行如下推导：

其中：ce是等效阻尼系数：u是运动速度.

等式两边同时乘以2倍的运动位移h：

变换得：

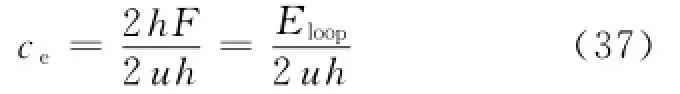
其中：El OOp是示功图的面积，即1个行程里阻尼力的消耗功.

定义可调倍数β′为：

3　结果讨论

3.1速度分布

在h0=3mm，u0=200mm/s，τ0=4k P a下，计算得出R0=10.8mm.分别计算不同半径位置处的

速度分布，得出图3的结果.

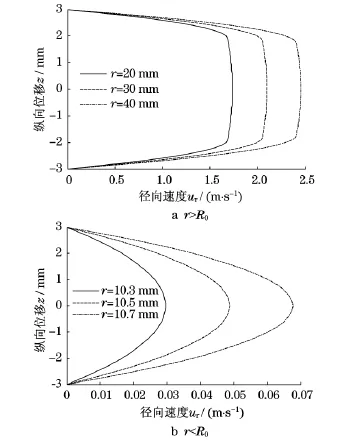
图3　径向速度分布Fig.3 Radial velocity distribution

由图3a可以看出，在r＞R0的区域内，由于存在屈服区和未屈服区，同一半径处的速度分布中间未屈服区速度变化小，上下屈服区的速度变化大，整体形成一个类似“塞子”的剖面分布.中间未屈服区的流体基本整体往外流动，速度转折点就是屈服分界面所在的位置.图3b反映r＜R0的速度分布，由于没有未屈服区的存在，因而速度没有明显的转折，速度分布为光滑的曲线，中间位置速度大，上下位置速度小.

3.2压力梯度分布

3.3屈服面位置

图5反映了以间隙中间平面为对称面，上下间隙内屈服面的情况.在r=R0处，屈服面位置zy并不等于3mm，这是由于从式（18）到式（19）的近似过程中，采用的是渐近线作为曲线的近似，r越大，近似误差越小，结果越精确，在本文中R=50mm，并没有远大于h，因而存在误差.

另一方面，τ0越大，磁流变液成链的结构越强，分散磁流变液内部有序颗粒所需的力就越大，因而，在其他因素不变的情况下，屈服面越靠近上下极板，中间的未屈服区厚度越大，“塞子”面积越大，同时，R0越大，远离圆心.

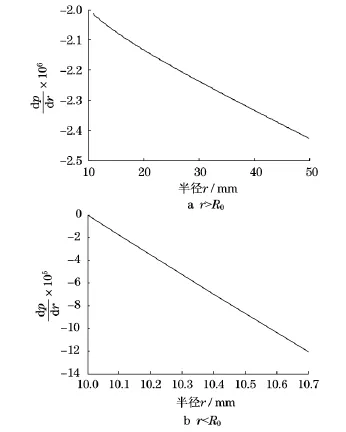
图4　压力梯度分布Fig.4 Pressure gradient distribution

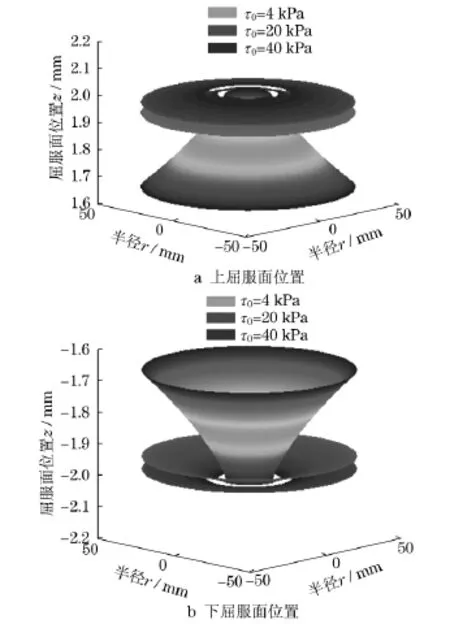
图5　屈服面位置Fig.5 Yield layer position

3.4阻尼力分析

图6分析了阻尼力的影响因素.由图6可以看出，初始间隙h0，挤压速度u0和磁流变液剪切屈服强度τ0都会影响阻尼力大小.

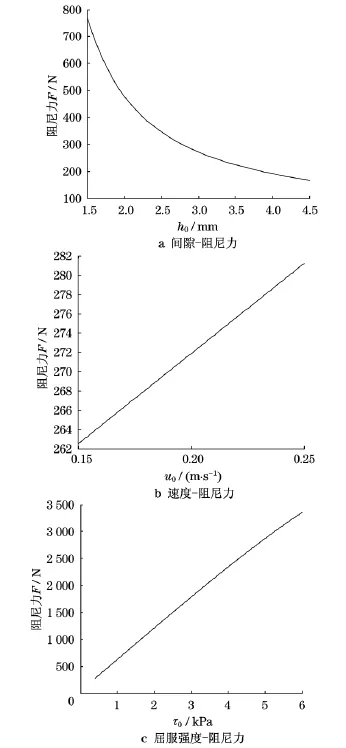
图6　剪切阻尼力单个影响因素分析Fig.6 Analize on single factor of damping force

挤压式磁流变减振器阻尼力大小随着初始间隙增大而减小，随着挤压速度增大而增大，随着磁流变液剪切屈服强度提高而增大.表1反映了上述3个因

素分别对阻尼力影响的权重大小，以阻尼力变化率与单个因素的变化率之比的大小来找出影响阻尼力的最大权重.表1中，Δ F=（Fm a x-Fm i n）/Fm i n；Δ h0= （h0m a x-h0m i n）/h0m i n；Δ u0，Δ τ0与此类似.

表1　单个因素对阻尼力的影响权重Tab.1 Influence of single factor on damping force

由表1可见，初始间隙影响阻尼力的权重最大，挤压速度影响阻尼力的权重最小，这正好从理论上说明了挤压式减振器的特性，即挤压式磁流变阻尼器属于小位移大阻尼的减振器，微小的位移变化就会显著改变阻尼力的大小.

图7说明了双因素相互作用对挤压式减振器阻尼力的共同影响.

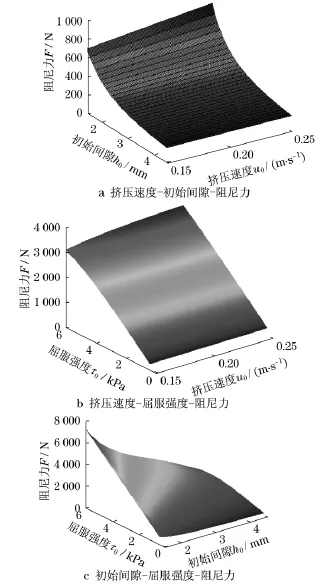
图7　阻尼力双影响因素分析Fig.7 Analize of double factors on damping force

由图7可以看出，初始间隙h0和磁流变液剪切屈服强度τ0对减振器阻尼力影响更大.这两个因素共同作用的效果要大于单个因素的影响效果，如图7c反映的阻尼力结果大于图7a和图7b反映的阻尼力结果.这说明，实际设计减振器时，为了获得最大的阻尼力，初始间隙h0应尽可能小，磁流变液剪切屈服强度τ0应尽可能大.

3.5示功特性

从挤压式减振器阻尼力的影响因素可以看出，阻尼力随着圆盘间隙的减小而增大.以圆盘间隙中间平面为对称面，挤压盘在中间上下运动，向下运动时，负向位移增大，距离下圆盘间隙减小，反向阻尼力增大；向上运动时，正向位移增大，距离上圆盘间隙减小，正向阻尼力增大.因而，该减振器的示功特性出现如图8所示的特征.这一特征说明，减振器在运动的上下两个端点出现阻尼力极值.从一个端点运动到另一个端点的过程中，阻尼力不断增大，相比于常见的剪切阀式减振器，能更快地衰减振动的能量.

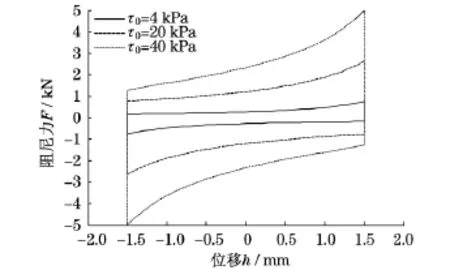
图8　示功图Fig.8 Indication resul

3.6可调倍数

由图9可以看出，减振器的等效阻尼系数随着磁流变液剪切屈服强度的提高而增大，也就是随着电流的增大而增大，由式（38）可算出其可调倍数β′最大可达9.7947.

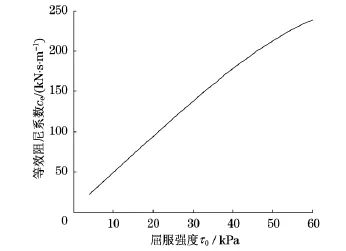
图9　等效阻尼系数Fig.9 Equivelant damping coefficient

4　结语

（1）挤压式磁流变减振器运动过程中，圆盘间的磁流变液受压分为屈服区和未屈服区两个部分，整体形成类似“塞子”的速度剖面向外流动，且随着磁流变液剪切屈服强度的提高，未屈服区的厚度增大，屈服分界面与圆盘的交点向外移动.

（2）根据双黏度模型，ηγ和η相差102个数量级，造成r＞R0和r＜R0两个区域内压力梯度相差101的数量级.因而，整个圆盘半径方向上压力梯度相差很大.

（3）挤压式磁流变减振器的阻尼力受初始间隙、挤压速度和磁流变液剪切屈服强度的共同影响，其中初始间隙的影响权重大于磁流变液剪切屈服强度及挤压速度的影响权重，从理论上证明了挤压式磁流变减振器是小位移大阻尼的减振器.

（4）挤压式磁流变减振器的等效阻尼系数随电流的增大而增大.在τ0=60k P a时，其可调倍数可达9.7947.

［1］ 闵峰，孙亮，王利伟，等.挤压式磁流变阻尼器示功特性［J］.重庆理工大学学报：自然科学版，2012，26（6）：13-17.

MIN Feng，SUN Liang，WANG Liwei，et al.Indication characteristic of squeeze-type magnetorheologic grease damper［J］.Journal of Chongqing University of Technology：Natural Science，2012，26（6）：13-17.

［2］ 刘勇，周瑾，徐龙祥.一种小位移大阻尼力磁流变阻尼器的设计与研究［J］.机械工程与自动化，2009（3）：29-31.

LIU Yong，ZHOU Jin，XU Longxiang.Design and research of MR damper for small displacement &big damping force［J］.Mechanical Engineering &Automation，2009（3）：29-31.

［3］ 路国平，邓国红.磁流变液在平行圆盘间的挤压流动分析［J］.重庆理工大学学报：自然科学版，2011，25（12）：55-59.

LU Guoping，DENG Guohong.Squeeze flow analysis of magnetoreological fluids between two parallel disks［J］.Journal of Chongqing University of Technology：Natural Science，2011，25（12）：55-59.

［4］ 廖荣昌，骆静，李锐，等.基于圆盘挤压模式的磁流变液阻尼器特性分析［J］.中国公路学报，2010，23（4）：107-112.

LIAO Rongchang，LUO Jing，LI Rui，et al.Characteristic analysis for magnetoreological fluid damper based on disksqueeze mode［J］.China Journal of Highway and Transport，2010，23（4）：107-112.

［5］ 郭朝阳.磁流变液法向力及减振器研究［D］.合肥：中国科学技术大学，2013.

GUO Chaoyang.Study on normal force of magnetoreological fluid and magnetoreological damper［D］.Hefei：University of Science and Technology of China，2013.

［6］ 章新杰.磁流变挤压悬置动态特性研究及其在汽车仿真中的应用［D］.长春：吉林大学，2011.

ZHANG Xinjie.Research on the dynamic property of amagnetoreological squeeze mount and its applicationsimulation on a vehicle ［D ］. Changchun： JilinUniversity，2011.

［7］ 杨仕普，任玲，朱克勤.平行圆盘间电流变液的挤压流研究［J］.功能材料，2006，37（5）：690-696.

YANG Shipu，REN Ling，ZHU Keqin.A study of squeeze flow of ER fluis between two parallel disks［J］.Function Material，2006，37（5）：690-696.

［8］ 路国平.汽车发动机用磁流变隔振器的分析和设计［D］.重庆：重庆理工大学，2012.

LU Guoping.Analysis and design of magnetoreological isolator used on automobile engine ［D］.Chongqing：Chongqing University of Technology，2012.

作者简介：陈 克（1965-），男，教授，博士.E-mail：chen_ke@163.com

Study on mechanics model of squeeze flow type ofmagnetoreological fluid damper

YAO Jun，ZHANG Jin-qiu，JIA Jin-feng，LIU Yi-le
（Bragade of Armorment Trial and Training，Academy of Armed Force Engineering，Beijing 100072，China）

In order to solve the problem that the damping force of shear-valve type of magnetoreological fluid damper is limited，a mechanics model of squeeze flow type of magnetoreological fluid damper is established.A damping force expression is concluded and the equivelant damping coefficient as well as the adjustable ratio are defined.According to deduced expression，the flow pattern of magnetoreological fluid intwo parallel disks is analized and the factors which relate to damping force are found out.Theanalysisresult proves that the squeeze flow type of magnetoreological fluid damper belongs to those which cangenerate high damping force in small displacement and it reaches 5 000N with only 3 mm displacement.Besides，the adjustable ratio can be reach 9.794 7.

damper； squeeze flow； damping force； equivelant damping coefficient；adjustable ratio

T B 381

A

1672-5581（2015）06-0497-07

姚 军（1991-），男，硕士.主要从事智能材料与振动控制研究.E-mail：2013yaojun@sina.com