基于A D AMS仿真的机器人用高精度RV减速器轮齿间隙研究*

奚 鹰，张 攀，卜王辉，华滨滨，王志成，柳先辉（同济大学机械与能源工程学院，上海0804；.同济大学电子与信息工程学院，上海0804）

基于A D AMS仿真的机器人用高精度RV减速器轮齿间隙研究*

奚 鹰1，张 攀1，卜王辉1，华滨滨1，王志成2，柳先辉2
（同济大学机械与能源工程学院，上海201804；2.同济大学电子与信息工程学院，上海201804）

为了保证机器人用高精度R V减速器的运动精度、扭转刚度、传动效率、总体回差和承载能力等要求，分析了摆线轮各齿的接触变形关系，计算了摆线轮齿与针齿的啮合力，进而获得了摆线轮与针轮的同时啮合齿数.采用UG软件建立了R V-40E型减速器模型，并进行A D AM S动力学仿真，探求了含有初始间隙的R V减速器传动时的啮合齿数，为提高减速器整体的传动稳定性、承载能力、扭转刚度等性能提供了理论基础.

R V减速器；啮合齿数；虚拟样机；工业机器人

机器人用高精度R V传动与传统的传动不同，它的传动比大，承载力高，刚度较大，同时运动精度高，回差小［1］，因此其在机器人中获得广泛应用.摆线轮是R V减速器中的核心部件，其齿形需保证瞬时传动比恒定，高传动精度，还要使得摆线轮齿形与针轮齿间的侧隙满足间隙回差要求，且同时需保证摆线齿与针齿的同时多齿啮合，因为这样可以使得轮齿啮合刚度增大，传动更加平稳.

为了达到这些要求，摆线轮必须要修形.本文采用理论计算和虚拟仿真结合的方式，分析经过修形组合之后的摆线轮与针齿的啮合齿数以及轮齿受力情况，为探求提高啮合刚度和传动稳定性的新方法提供理论基础.

1　RV减速器的技术参数

R V减速器的基本传动方式是行星轮系传动，但它与一般的减速器不同，采用的是摆线针轮传动，其齿廓是外摆线齿廓.图1为R V减速器的整体结构图，其基本参数如表1所示［2］.

图1　RV减速器的组成结构图Fig.1 Composition structure diagram of RV reducer

表1　RV-40E减速器基本技术参数Tab.1 Basic technical parameters of RV-40Ereducer

2　理论探求同时啮合齿数

2.1摆线轮修形方式的选取

本次研究采用的摆线齿轮，选择正移距负等距的修形方式，移距修形量Δrp=0.008mm，等距修形量Δrr p=-0.002mm，没有使用转角修形.摆线轮理论齿廓曲线的参数方程式为［3］：

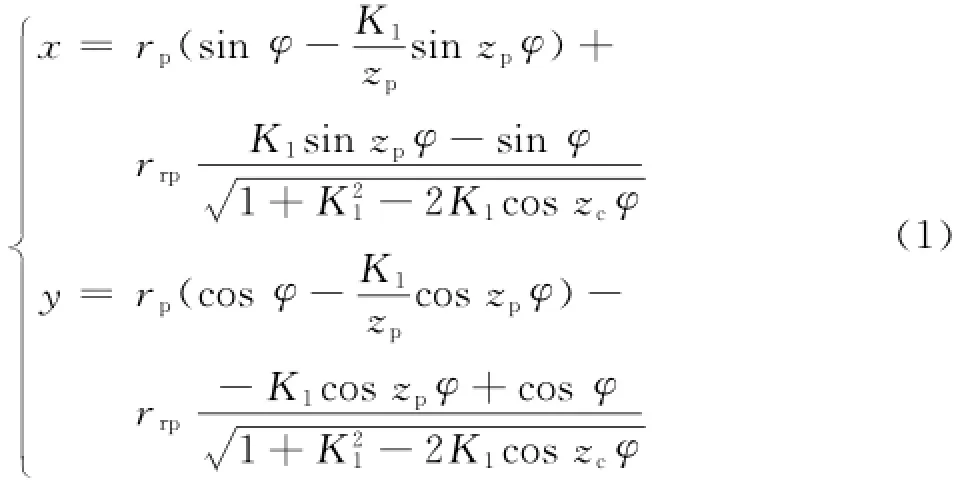
其中：K1为短幅系数，K1=a zp/rp（a为偏心距）；zp为针轮的齿数；zc为摆线轮的齿数；rp为针齿轮中心圆半径；rr p为针齿套半径，本文中均为针齿销半径.

R V-40E摆线轮基本参数如表2所示.

表2　RV-40E摆线针轮基本技术参数Tab.2 Basic technical parameters of RV-40Ecycloid

将表2所示摆线轮参数代入式（1）可以得到修形后的摆线轮齿形方程，见式（2）：

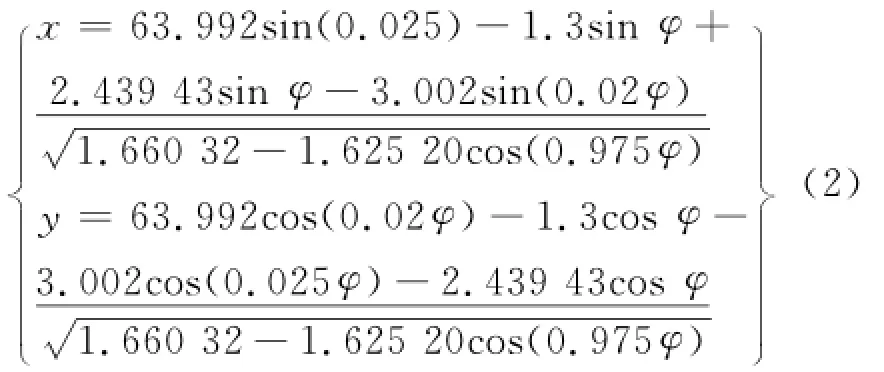
将修形后的齿形与标准齿形的曲线用MAT L A B绘制出来，取1个齿的齿顶部分，经过放大之后的对比情况如图2所示.

图2　标准齿形与修形齿形对比图Fig.2 Comparison of standard tooth and modification tooth

图2中，标准摆线轮的齿形曲线要明显大于修形后的摆线轮曲线.这样在修形后的摆线轮与标准针齿啮合时就会存在啮合间隙.间隙的存在有利于补偿制造误差，保证齿间的润滑，减少噪声，使得运行更加平稳，但是也造成了同时啮合齿数的变化. 2.2计算初始间隙

摆线轮传动初始间隙的分布规律为：标准摆线轮及只经过转角修形的摆线轮与标准的针齿啮合，同时啮合齿数在理论上都可达到约为摆线轮齿数的一半［4］，但在经过等距移距修形或者移距修形后，若不考虑零件弹性变形的补偿作用，则多齿啮合的情况不再存在，而变为某一轮齿和针齿接触，其余的摆线齿轮和针齿之间都存在着大小不同的初始间隙［5］.

首先采用理论计算方法.摆线轮经过等距修形以及移距修形，法线方向的初始间隙Δφi可按下式计算［6］：

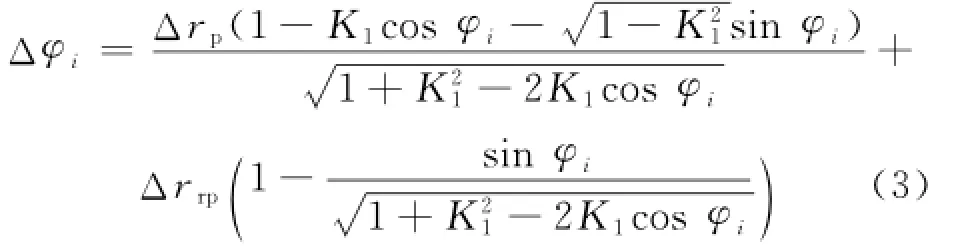
式中：φi为第i个针齿相对于转臂OpOc的转角，（°）.

当Δφi=0时，可以得到：

式中的φ0是使初始间隙为零的角度，空载时，只有在（或最靠近）φ0=c Os-1K1处的1对齿啮合.

以1°为步长，取0～180°部分（即摆线轮的左半边，如图3所示）进行研究.由于共有40个针齿，因此每隔9°就有1个针齿存在，由式（2）可以得到每个角度的初始啮合间隙，但是并不是每1°都能对应1个针齿的，这并不影响接下来的研究.计算出初始啮合间隙后再通过MA T L A B绘出其图像，如图4所示. 2.3判定摆线轮与针轮同时啮合的齿数

图3　针齿均布图（1～20为针齿号）Fig.3 Needle and teeth chart（1-20for the pin tooth number）

由于针轮与摆线轮在啮合时肯定都存在弹性变形，这样就使得摆线轮各个啮合点的公法线方向存在一个总变形或在待啮合点法线方向存在一定的位移，当这个总变形或者位移大于该位置对应的初始间隙时，则在这个角度范围内的各齿都将啮合，反之就不会进入啮合.由此可以计算啮合齿数.

设传递载荷时，每片摆线轮受到的转矩为Tc，

图4　摆线轮初始啮合间隙曲线Fig.4 Cycloid initial teeth clearances curve

摆线轮会出现接触变形，针齿销会出现弯曲变形，摆线轮摆过一个角度β，则摆线轮各啮合点的公法线方向总变形或待啮合点法线方向的位移为［6］：

δi=liβ（i=1，2，…，zp/2）（5）

式中：β为受到载荷作用后，由于零件变形引起的摆线轮的转角，r a d；li为第i个针齿啮合点的公法线或待啮合点的法线至摆线轮中心Oc的距离，mm.设受力最大的一对摆线轮齿与针轮齿的接触变形和针齿销的弯曲变形之和为δm a x，其啮合点公法线到摆线轮中心Oc的距离为lm a x，可以得到式（6）：

结合各个数据以及公式，可以计算出摆线轮与针齿轮的接触变形和针齿销的弯曲变形之和δi，并通过MAT L A B软件绘出其图像如图5所示.图5中，在接近φ0=c Os-1K1处摆线轮与针齿轮的接触变形和针齿销的弯曲变形之和最大，即说明该处受力最大，产生的变形与位移最大，而在该处两侧的啮合点受力逐渐减小.若将由于齿形修形所产生的第i对轮齿沿待啮合点法线方向的初始间隙Δφi与摆线轮在各啮合点公法线方向的总变形或待啮合点法线方向的位移δi绘制在1张图中，可以得到图6.

图6中2条曲线有2个交点，分别在3.18°和150.02°处.根据前述摆线轮与针轮啮合的原理，在3.18°至150.02°之间的摆线轮齿与针轮齿是啮合的，由于针轮有40个轮齿，故每9°有1个轮齿，因此在该角度区间共有16个轮齿，所以同时有16个摆线轮齿与针轮齿处于啮合状态.

3　轮齿啮合受力分析

修形摆线轮与针轮啮合时的受力分析：空载时，经过修形的摆线轮在（或最接近）φ0=c Os-1K1处接触，其余各齿与针轮齿在沿待啮合点的法线方向上均存在初始间隙，且大小不同，这种差别在修形量较大时特别明显，因此，这时就不能假设各齿受力Fi与总变形δi=liβ成线性正比关系，只能假设Fi与δi-Δφi成线性正比关系.这一假设考虑了起到主要作用的初始间隙以及受力弹性变形和弯曲变形，因而用于受力分析足够准确.

图5　摆线轮受载后沿啮合点法线方向的总位移曲线Fig.5 Total displacement curves of cycloid along the meshing point normal direction under load

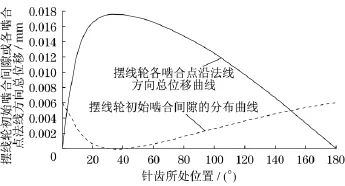
图6　初始啮合间隙与受载后沿啮合点法线方向总位移g.6 Initial clearances and total displacement contrast

图7　摆线轮的受力图Fig.7 Forceanalysis of cycloid

图7为摆线轮的受力图，由于同时啮合的齿比较多，故只标出其中几个啮合力示意一下.

在同时啮合受力的各个齿中，第i个齿受力Fi可用下式表示［6］：

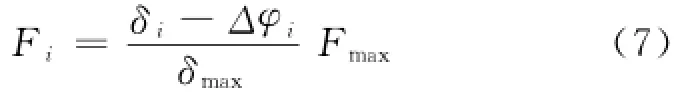
因为在（或最接近）φ0=c Os-1K1处的齿最先接触受力，很明显，该齿在同时受力的各齿中受力最大，故以Fm a x表示该齿受力.

利用计算机迭代的方法计算得到各个齿受力的大小，用MAT L A B绘图可得图8.图8中，在接近φ0=c Os-1K1处的齿受力最大，与理论符合得很好.

图8　摆线轮各啮合齿受力曲线图Fig.8 Tooth forces graph on cycloid

4　摆线轮虚拟样机的建立

4.1实体模型的建立以及简化

利用UG进行三维实体建模.根据摆线轮的方程参数化建立了摆线轮，同时对针轮、输入轴、法兰、行星架、外壳等各部件进行了三维实体建模，并把各零件组装成装配图.为了节约存储空间，提高运算速度，对模型进行了简化，例如：用圆柱代替渐开线齿轮并与曲柄轴合为一体；法兰与行星架合为一体，删除挡圈、轴承、螺栓等无关部件；删除所有不影响传动的倒角、圆角.简化模型如图9所示（隐藏行星架）.模型建立后还需要进行零件干涉检查，包括静态干涉检测和动态干涉检测，本次仿真已调整至不存在任何干涉.

4.2模型的导入和定义

仿真分析方法：将U G简化后的装配模型另存为X_T格式，再通过A D AM S的I m p Or t命令导入A D AM S软件来进行运动仿真和分析.由于U G和A D AM S所用的P a r a s Ol i d格式为两者内核格式，因此本次仿真的可信度较高.在UG中已经将各部件装配完毕，因此各部件的位置已经调整完毕，在A D AMS中只需要调整各部件的颜色和材料特性.

图9　RV-40E简化模型（隐藏行星架）Fig.9 RV-40Esimplified model（planet carrier hided）

材料设置如表3所示.

本次共导入刚体47个，约束50个，接触82个，旋转驱动1个，齿轮副2个，与模型自检结果一致.设置负载扭矩为572N·m，设置旋转驱动输入转速为525r/m i n，定义输入转速函数为1s内缓慢增长的曲线，并至1s内恒定及F（t i m e）=3150d *t i m e*s t e p（t i m e，0，0，0.1，1）［8］，定义负载扭矩为s t e p（t i m e，1.0，0，1.5，572000）.自行定义5s仿真时间，500步仿真步数.

5　虚拟样机仿真结果

图10为R V减速器空载时输入轴角速度曲线.由图10可见，输入轴转速从0到1s内缓慢增加，加速至输入转速后角速度恒定.图11为输入轴角加速度曲线，由图11可知，角加速度至1s时变为0.

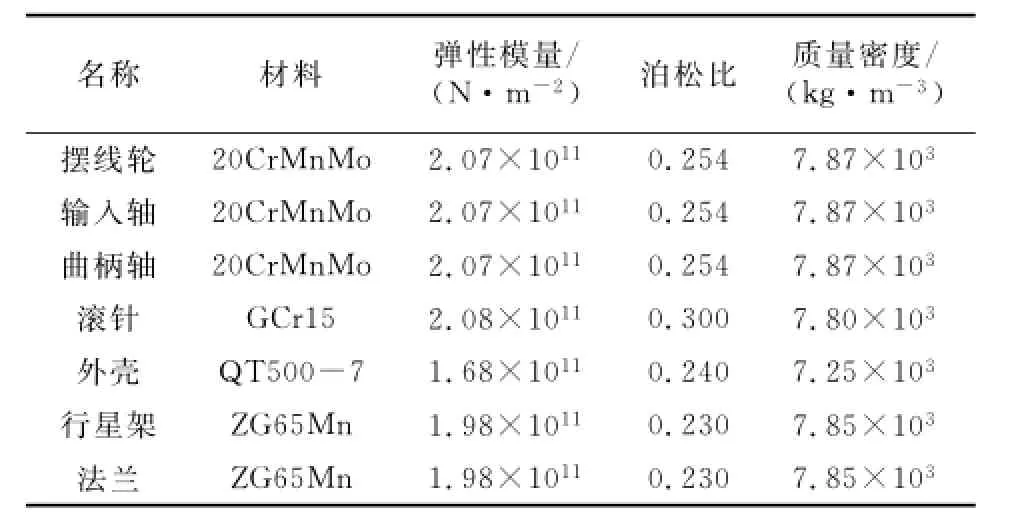
表3　RV减速器各个零件材料特性Tab.3 Material properties of various parts of RV reducer

4.3约束的添加

约束的类型如表4所示，接触的类型如表5所示，并给输入轴和2个直齿轮设置2个齿轮副［7］.

表4　RV减速器仿真的约束类型Tab.4 Constraint types of RV reducer simulation

表5　RV减速器仿真的接触设置类型TTab.5 Contact setting types of RV reducer simulation

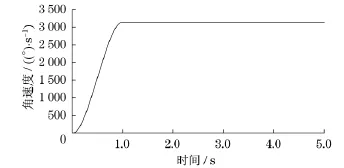
图10　输入轴角速度曲线Fig.10Angular velocity curve of input shaft

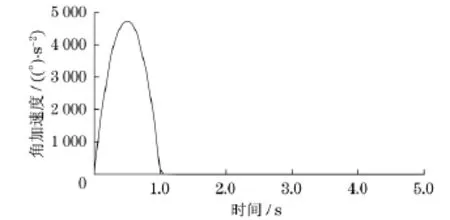
图11　输入轴角加速度曲线Fig.11 Angular acceleration velocity curve of input shaft

图12为输出轴（行星架）角速度曲线，可见输出轴角速度在缓慢增加后，达到输出转速后恒定.图13为输出轴（行星架）角加速度曲线，由于各部件存在冲击振动，因此该角加速度存在波动.

如图14所示，最终仿真所得经修形后的减速器摆线轮与针轮同时接触的数量有16对，即摆线轮与滚针同时啮合齿数为16对，这与理论计算的同时啮合齿数相同.由关键部件的仿真结果和理论计算结果可知，本次仿真结果正确合理并且所得结果比较准确稳定.

图12　输出轴（行星架）角速度曲线Fig.12 Angular velocity curve of output shaft

图13　输出轴（行星架）角加速度曲线F i g.13A n g u l a r a c c e l e r a t i On v e l Oc i t y c u r v e Of Ou t p u t s h a f t

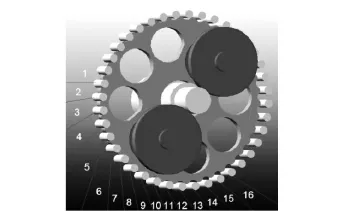
图14　RV减速器A D AMS接触动力学仿真Fig.13 Angular acceleration velocity curve of output shaft

6　结语

（1）机器人用R V减速器需要多齿啮合，同时还要有合理的啮合间隙来补偿误差及满足润滑条件，因此探求摆线轮与针轮同时啮合齿数具有重要意义.

（2）本文从理论计算和虚拟样机仿真两方面对摆线针轮传动中的针齿啮合受力和啮合齿数进行了计算和分析.

（3）本文为研究提高同时啮合齿数的齿廓修形方法提供了理论基础，为在保证精度的前提下有效提高传动平稳性、承载能力、扭转刚度和传动效率提供了理论支撑.

［1］ 松本和幸.偏心差动方式减速机“RV减速机”［J］.机械设计（日），1987，31（8）：58-64.

MATSUMOTTO Kazuyuki.Differentially eccentric reducer“RV reducer”［J］.Machine Design（Japan），1987，31（8）：58-64.

［2］ 齿轮手册编委会.齿轮手册［M］.北京：机械工业出版社，2008：112-115.

Gear Manual Editorial Board.Gear manual［M］.Beijing：Mechanical Industry Press，2008：112-115.

［3］ 庞素敏，陈小安.摆线轮齿廓参数化设计及动力学仿真［J］.现代制造工程，2008（3）：50-53.

PANG Sumin， CHEN Xiaoan. The cycloid profile parameterization design and dynamic verification［J］.ModernManufacturing Engineering，2008（3）：50-53.

［4］ 何卫东，李欣.机器人用高精度RV减速器中摆线轮的优化新齿形［J］.机械工程学报，2000，36（3）：51-55.

HE Weidong，Li Xin.A new optimized tooth of the cycloid in high-precision robot RV reducer ［J］. Mechanical Engineering，2000，36（3）：51-55.

［5］ YU Hongliu，YI Jinhua，HU Xin，et al.Study on teeth profile modification of cycloid reducer based on non-hertz elastic contact analysis［J］.Mechanics Research Communications，2013，48：87-92.

［6］ 李力行.摆线针轮行星传动的齿形修正及受力分析［J］.大连铁道学院学报，1984（4）：29-40.

LI Lixing.Profile modification and behavior analysis of cycloid transmission［J］.Journal of Dalian Railway Institute，1984（4）：29-40.

［7］ 陈来利，姚辰龙，王海生.基于A D AM S的RV减速器虚拟样机设计及仿真分析［J］.机械工程师，2013（9）：102-105.

CHEN Laili，YAO Chenlong，WANG Haisheng.Virtual prototyping and simulation analysis of the RV reducer based on ADAMS［J］.Mechanical Engineers，2013（9）：102-105.

［8］ 吴素珍，何卫东，陈卓，等.RV减速器虚拟样机仿真技术研究［J］.机械传动，2014（9）：20-23.

WU Suzheng，HE Weidong，CHEN Zhuo，et al.RV reducervirtual prototype simulation［J］.Mechanical Transmission，2014（9）：20-23.

Analysis of teeth clearances in robotic high precision RV reducer based on ADAMS

XI Ying1，ZHANG Pan1，BU Wang-hui1，HUA Bin-bin1，WANG Zhi-cheng2，LIU Xian-hui2
（1.School of Mechanical Engineering，Tongji University，Shanghai 201804，China；School of Electronic and Information Engineering，Tongji University，Shanghai 201804，China）

There are clearances between cycloid gear and pins in robotic high precision RV reducer.To ensure the output accuracy，torsional stiffness，transmission efficiency，overall hysteresis，carrying capacity and other requirements，the meshing teeth between cycloid gear and pins should be as many as possible iflubricating condition is satisfied.Hence，the deformation relationship among cycloid teeth is analyzed，andthe number of meshing teeth is calculated based on the meshing force between the cycloid tooth and thepin.The UG software is adopted to model RV-40E reducer and the ADAMS software to perform dynamicsanalysis.The number of meshing teeth with initial clearances is studied based on virtual prototypingsimulation.A theoretical foundation for the improvement of the overall stability，carrying capacity，torsional stiffness and other performances of the RV reducer is provided.

RV reducer；meshing teeth；virtual prototype；industrial robot

T P 242.2

A

1672-5581（2015）06-0509-06

国家自然科学基金资助项目（51475331）；“十二五”国家科技支撑计划项目（2012B A F 12B 01）；上海市科委资助项目（13111101704）

奚 鹰（1957-），男，博士，教授.E-mail：yingxi@tongji.edu.cn