双调节挤压式磁流变减振器特性研究

2017-11-07张进秋毕占东刘义乐

振动、测试与诊断 2017年5期

关键词：阻尼力滚珠丝杠

姚军，张进秋，毕占东，刘义乐

(装甲兵工程学院装备试用与培训大队北京，100072)

10.16450/j.cnki.issn.1004-6801.2017.05.010

双调节挤压式磁流变减振器特性研究

姚军，张进秋，毕占东，刘义乐

(装甲兵工程学院装备试用与培训大队北京，100072)

为了解决挤压式磁流变减振器大阻尼小位移这一特性不适用于车辆的不足，设计外部滚珠丝杠结构，建立运动学、动力学模型，理论计算和仿真分析减振器外部连杆运动速度、位移和磁流变液剪切屈服强度对阻尼力的影响。对该减振器的示功特性和连杆长度比对阻尼力的调节作用进行了分析，最后进行了台架实验。实验得到该减振器不同电流下的示功图，和理论分析的结果基本一致，说明该阻尼力表达式正确，滚珠丝杠结构可以增大挤压式减振器位移和阻尼力的调节范围，使之适用于车辆，并使其具备机械电磁双调节模式。

挤压式；滚珠丝杠；磁流变减振器；机械电磁调节；阻尼力

引言

磁流变减振器(magnetoreological damper, 简称MRD)是应用了磁流变液(magnetoreological fluid, 简称MRF)这种可控流体的新型减振器。在不同磁场下，磁流变液剪切屈服强度不同，迫使磁流变液流动的剪切力也就不一样，也就是磁流变减振器所提供的阻尼力可变。因而，通过控制外加磁场，便可达到磁流变减振器阻尼可调的目的。正是这一具有重要工程应用价值的特性，引起磁流变减振器的广泛研究，并成功应用在多种场合[1]。

根据磁流变液的流动模式，磁流变减振器可分为剪切式，阀式，挤压式以及两者相互间的混合工作模式。Potnuru等[2-3]对剪切模式下筒式和叶片式减振器进行了改进和优化，实现阻尼力和体积比最大化，但磁流变液用量大。基于阀式流动的磁流变减振器[4-5]按照多级串联的思想提高了磁流变减振器的阻尼力，但调节范围有限。章新杰等[6-7]研究了挤压式磁流变减振器在发动机隔振系统中的应用，发现该类减振器可产生的阻尼力很大，磁流变液用量很少；此外，基于挤压薄膜的滚子减振器[8-9]也可在提供较大阻尼力的同时减少磁流变液的用量。这说明挤压式磁流变减振器克服了剪切式式减振器的不足，但挤压式减振器自身也存在不足，主要是其大阻尼小位移特性适用范围受限。为了解决挤压式这一问题，借鉴主动悬挂系统中滚珠丝杠结构，齿轮齿条结构和行星齿轮结构[10-11]的应用，将滚珠丝杠结构应用在减振上，并对其外特性进行研究。

1 挤压式磁流变减振器力学模型

1.1 挤压式减振器结构

为了解决剪切式磁流变减振器的磁流变液用量多而实际发生磁流变效应的量很少导致磁流变液利用率不高，以及阀式减振器阻尼力调节范围有限的不足，设计了带有滚珠丝杠的挤压模式减振器。

挤压式磁流变减振器的特点是小位移大阻尼，其外形结构呈扁平状，减振器内部空间主要是平行圆盘围成的空间，所需磁流变液少；同时，圆盘间的间隙也是减振器发生磁流变效应的区域，因而磁流变液利用率极高。为了满足车辆悬挂系统车轮动行程大的要求，利用滚珠丝杠将位移放大，阻尼力缩小，使减振器阻尼力调节范围增大，从而满足车辆减振器的要求，车用挤压式减振器结构如图1(a)所示。此减振器主要由圆盘形挤压式减振器和滚珠丝杠传动结构组成。滚珠丝杠结构通过两个连杆将大行程的直线运动转化为圆盘微小的挤压运动。挤压式减振器几何关系如图1(b)所示。

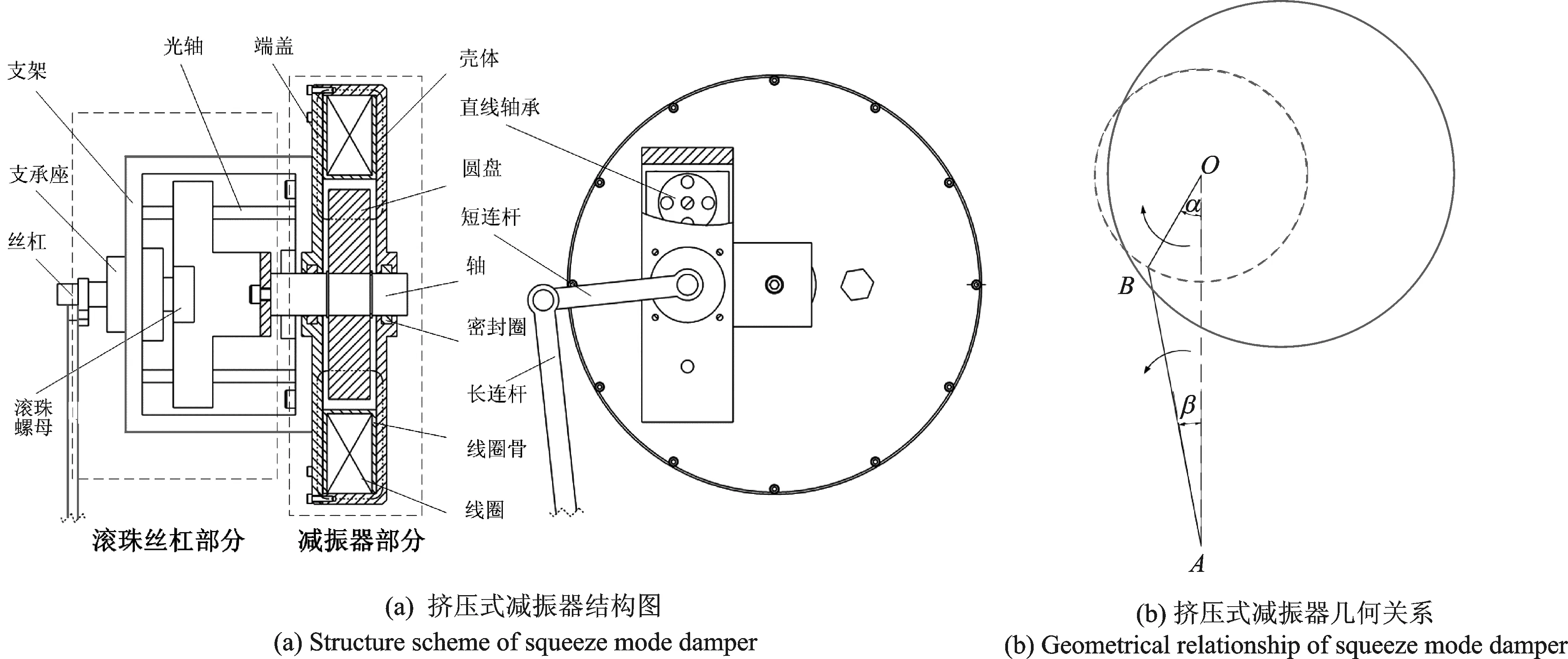
图1 车用挤压式减振器Fig．1 Squeeze mode damper used on a vehicle

1.2 连杆运动学方程

如图1(b)所示，连杆OA长度为l，转动角速度为w，连杆OA与竖直方向夹角为α，连杆AB长度为L，转动角速度为wAB，质量为mAB，连杆AB与竖直方向夹角为β。A点与O点竖直，且A点沿竖直方向运动。根据运动学关系，挤压式减振器上A点和B点的速度，加速度和力的关系可表示为

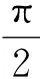
(1)

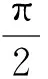
(2)

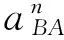
(3)

(4)

(5)

(6)

1.3 滚珠丝杠动力学方程

滚珠丝杠是将连杆的运动转化为减振器的挤压运动，选取丝杠和螺母的接触位置进行分析，将丝杠展开形成平面楔形，γ由丝杠的导程和直径共同决定，丝杠直径为d，质量为md，如图2所示。

根据刚体动力学理论有

Fjcosγ-F=mam

(7)

(8)

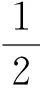
(9)

图2 滚珠丝杠力学关系Fig．2 Mechanic relationship of ball-screw

其中：Fj为螺母和丝杠间的挤压力；F为减振器的阻尼力；α=at/l表示丝杠旋转角加速度；am为减振器圆盘的加速度。

1.4 阻尼力方程

根据前期减振器内特性的研究，挤压式减振器的阻尼力可表示为

(10)

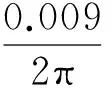
联立以上式子，得到该减振器提供的外阻尼力和位移以及速度的关系

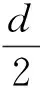
(11)

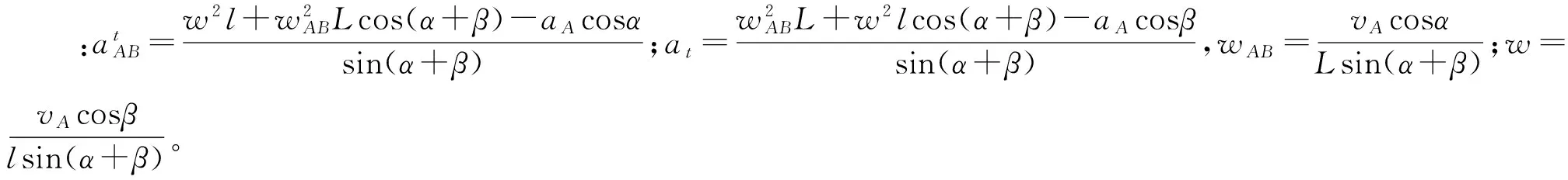
此时，建立起外阻尼力和外部位移以及速度的关系FA(s)和FA(vA)。

2 理论仿真分析

2.1 速度、加速度及剪切屈服强度对阻尼力的复合影响

考虑两个因素对阻尼力的复合影响，拟定连长杆L=400 mm，l=70 mm，丝杠导程10 mm，分别令旋转角α=π/2，磁流变液剪切屈服强度τ0=4 kPa，A点速度vA=1.6 m/s，计算阻尼力随另外两个因素变化的规律，分别得到图3(a)～( c)。

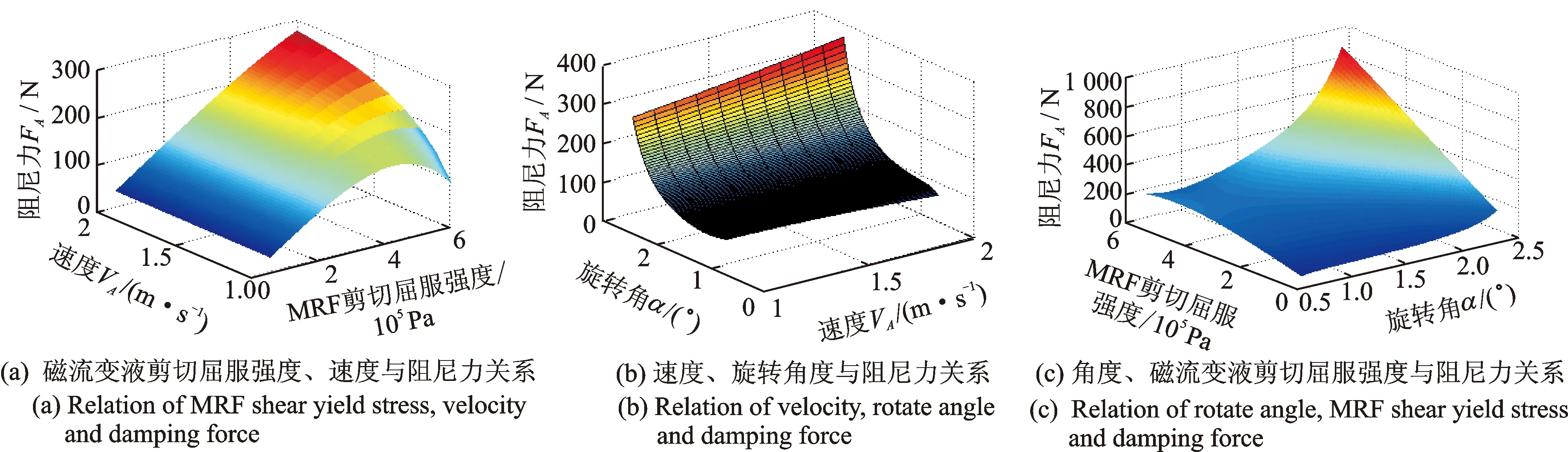
图3 复合因素影响Fig.3 Influence of two factors

图3(a)表示磁流变液屈服强度τ0和外部速度vA与外部阻尼力FA的关系。可以看出，速度较大时，阻尼力随剪切屈服强度增大而增大，速度较小时，由于R0增大已超过圆盘半径R，根据式(10)阻尼力减小，这与单个因素对阻尼力影响的图3(c)分析一致。

图3(b)为旋转角度α，外部速度vA对外部阻尼力FA的关系。外部阻尼力FA随着连杆旋转角度α和连杆端点运动速度vA增大而增大，但在不同的旋转角度或不同的运动速度下，阻尼力的增长率不同，旋转角越大，运动速度越大，阻尼力增长率越大，且旋转角对阻尼力的影响更大。

图3(c)表示不同旋转角α和MRF不同剪切屈服强度τ0对阻尼力FA的影响。对应不同旋转角，阻尼力随磁流变液剪切屈服强度增大的增长率变化不一致。旋转角较小时，MRF剪切屈服强度对阻尼力的影响不大；旋转角较大时，此时减振器内部间隙变小，磁流变效应明显，因而此时MRF剪切屈服强度对阻尼力的影响明显增大。

从以上的复合因素分析来看，由于外部滚珠丝杠和连杆的结构存在，A点阻尼力FA与A点位移s，A点速度vA和磁流变液剪切屈服强度τ0的关系变得复杂。位移s对阻尼力的影响本质上是旋转角α对阻尼力的影响。旋转过程中，当两根连杆OB和AB垂直，此时，AB与竖直方向夹角β最大，这一位置形成了阻尼力的一个临界点。外部速度vA和磁流变液剪切屈服强度τ0对阻尼力FA的影响，实际上是两者对减振器内部间隙处磁流变液屈服面位置所在半径R0的影响。R0不得大于圆盘半径，否则阻尼力将不再变化。理论计算上，根据式(10)，阻尼力将减小，因为出现了负值。

2.2 挤压式磁流变减振器示功特性

根据以上的分析，外部阻尼力FA受多个因素的相互影响。主要影响因素还是间隙处磁流变液剪切屈服强度的影响。设定旋转角α变化范围是3π/18～15π/18。示功图如图4所示。

图4 示功图Fig．4 Indication result

旋转角α在小于3π/18大于15π/18的作用域里，阻尼力随位移的增大的而增大，当应用车辆上时，表现为从偏离平衡位置最远处向平衡位置靠近时，阻尼力从最小逐渐增大。这一过程的意义在于使车辆尽快回到平衡位置，减振器继续从平衡位置向远处运动时，阻尼力增大，表现为尽可能保持车辆在平衡位置，增大偏离平衡位置的阻尼。相反过程具有同样的意义。

2.3 连杆长度对阻尼力的影响

由于外部机构的特殊作用，两连杆的长度对减振器也存在很大影响。定义长连杆对短连杆的长度比值是k，图5给出了不同的比值下，阻尼力和位移的关系。其中，长连杆长度为400 mm，在相同旋转角度下，k值越小，减振器阻尼力范围越大；k值越大，减振器阻尼力范围越小，且随着k值的增大，阻尼力变化范围幅度逐渐减小，从而形成机械调节阻尼力大小。

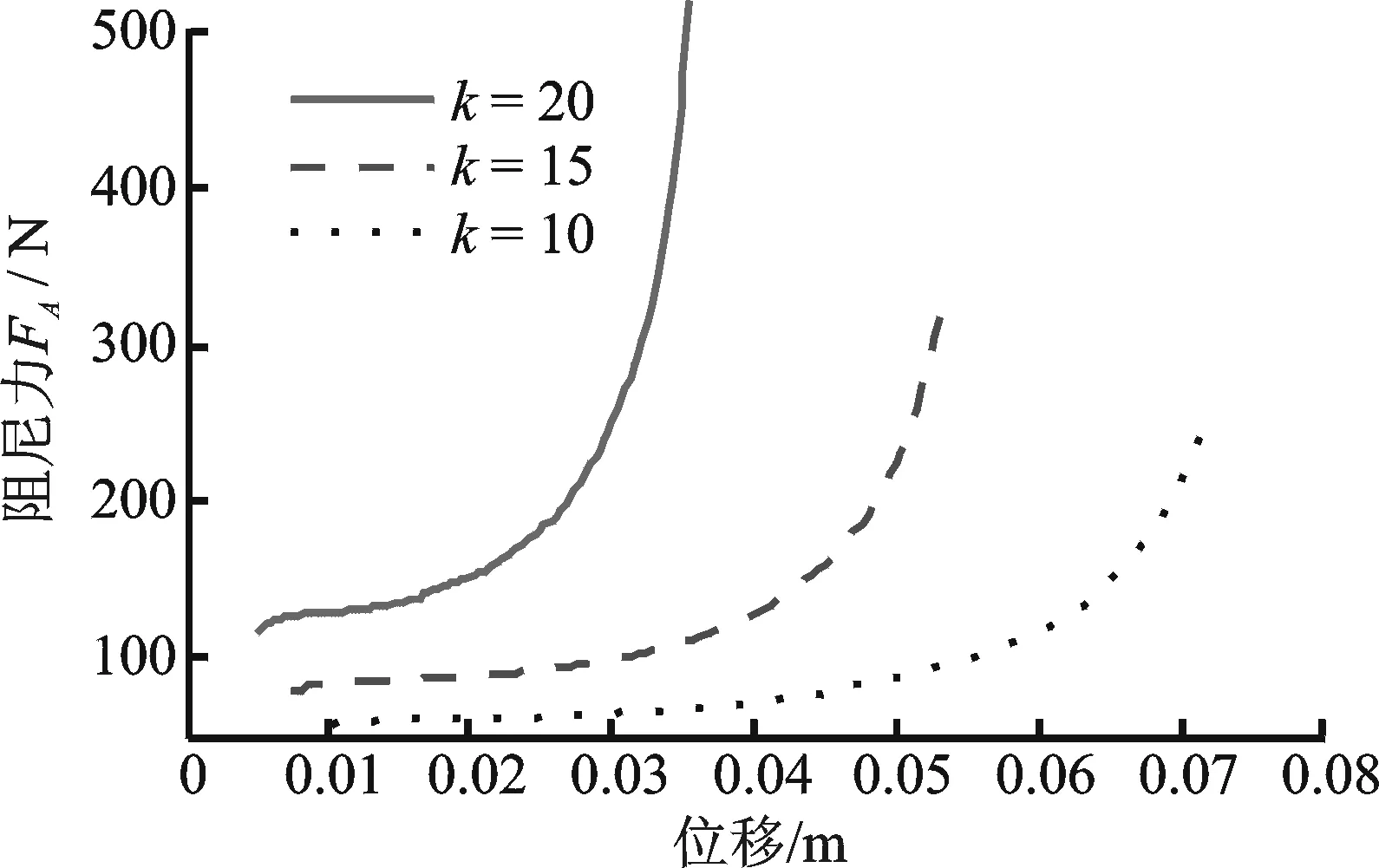
图5 连杆长度对阻尼力影响Fig.5 Influence on damping force of the length of connecting rod

3 实验验证

根据以上推导的理论模型，笔者设计了基于挤压模式的减振器模型，用于验证理论模型的正确性，采用滚珠丝杠结构将减振器内部的直线挤压运动转变为外部的旋转运动。其基本参数如表1所示。

表1 减振器基本参数

3.1 实验结果

实验主要检验推导理论模型的正确性，设定比值k较小，是考虑滚珠丝杠结构的受力特性，在小阻尼力范围进行试验，并和理论进行对比。重点分析磁流变液的剪切屈服强度对减振器阻尼力的影响。将实测数据与理论数据进行对比。图6为α=π/2的理论与实测数据的对比。

图6 数据对比Fig．6 Comparison of data

由于短连杆长度l=70 mm，比值k较小，因而滚珠丝杠结构将位移放大的幅度很大，则根据能量守恒，阻尼力就很小。从图中可以看出，实测数据与理论值接近，存在较大误差。在旋转角度α固定的前提下，减振器的阻尼力随着磁流变液剪切屈服强度的增大而增大，说明模型的正确性。为了更进一步分析理论模型的精确性，当有不同电流时，用减振器的往复运动过程形成的示功图分析模型的误差。

利用采集的数据，绘制不同电流时的示功图。从图7(a)明显看出，电流小，阻尼力小，电流大，阻尼力大，即阻尼力随线圈的电流增大而增大。图7(b，c，d)是不同电流时的示功图对比结果。实验结果在趋势上和理论基本一致，证实了所建模型的正确性，但还存在较大误差，且误差随着电流的增大而增大。

图7 示功图结果Fig．7 Indication result

3.2 误差分析

由于试验台液压油缸不能高速运动，虽然减振器的阻尼力随运动速度增大而增大，但是增大的幅度很小。图7(a)说明此实验减振器运动速度小于0.15 m/s。此速度经过滚珠丝杠转化为减振器的内部挤压速度，变化幅度很小，只有0.003 m/s。此外，所设计的减振器在电流I=2 A时，间隙处磁感应强度约为0.6 T，对应的磁流变液剪切屈服强度约为10 kPa。当速度恒定，磁流变液剪切屈服强度较小时，阻尼力随位移增大而增大，在旋转角较小时，也就是位移较小时，阻尼力变化不大，如图3(c)的分析结果。这就导致图7中位移初始位置位置存有较大的空白，形成较大误差。

同时，滚珠丝杠结构本身存在一个传递效率，约为90%～95%，而理论计算并没有考虑这一点，这也是误差来源之一。

4 结论

1) 挤压模式的减振器，结构呈扁平状，减振器内部空间主要是平行圆盘围成的空间，所需磁流变液少，同时，圆盘间的间隙也是减振器发生磁流变效应的区域，因而磁流变液利用率高。

2) 利用外部滚珠丝杠结构，可以将挤压式磁流变减振器的大阻尼小位移特性改变为适用于车辆的常规阻尼力和位移的特性。这一转换过程能量损失小，转换效率大。

3) 除了改变线圈电流大小而调节减振器阻尼力这一方法外，笔者所设计的减振器还可通过调节外部连杆的长度比改变减振器阻尼力和位移的相互关系，从而达到机械调节阻尼力的目的，具备机械电磁双调节模式。

[1] 卫丽君，李书. 磁流变减摆器对直升机空中共振的影响分析[J]. 振动、测试与诊断, 2013，33(6)：981-986.

Wei Lijun, Li Shu. Analysis of impact of MRD on resonate of helicopter[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(6): 981-986. (in Chinese)

[2] Potnuru M R, Wang X J, Mantripragada S, et al. A compressible magneto-rheological fluid damper - liquid spring system[J]. International Journal of Vehicle Design, 2013, 63(2/3): 256-274.

[3] 张进秋, 彭志召, 张建, 等. 叶片式磁流变液减振器结构设计与优化[J].振动、测试与诊断，2013，33(1)：132-137.

Zhang Jinqiu, Peng Zhizhao, Zhang Jian, et al. Design and optimization of vane magneto-rheological fluid damper[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(1): 132-137. (in Chinese)

[4] 廖昌荣，赵丹侠，刘琼. 面向轨道车辆抗蛇行振动的磁流变脂阻尼器设计与台架测试[J].振动与冲击，2013，32(4)：54-58.

Liao Changrong，Zhao Danxia，Liu Qiong. A design method of magneto-rheological grease damper for railway vehicle anti-hunting vibration and tests[J]. Journal of Vibration and Shock, 2013, 32(4): 54-58. (in Chinese)

[5] Liao Changrong，Zhao Danxia，Liu Qiong. A design methodology for a magnetorheological fluid damper based on a multi-stage radial flow mode[J]. Smart Materials and Structures, 2012, 21(8): 085005.

[6] 章新杰. 磁流变挤压悬置动态特性研究及其在汽车中的仿真应用[D].长春：吉林大学，2011.

[7] Zhao Danxia，Liao Changrong， Liu Qiong. Analytical study on damping performances of magnetorheological grease damper based on disk squeeze mode and experimental test[J]. Frontiers of Mechanical Engineering,2011, 6(3): 312-317.

[8] Hemmatian M, Ohadi A. Sliding mode control of flexible rotor based on estimated model of magnetorheological squeeze film damper[J]. Journal of Vibration and Acoustics, 2013, 135: 1-11.

[9] Hemmatian M, Ohadi A. Vibration behavior of lexible rotor system mounted on MR squeeze film damper with thermal growth effect[J]. Journal of Vibration and Acoustics, 2012, 134: 1-10.

[10] 王庆年，刘松山，王伟华，等. 滚珠丝杠式馈能型减振器的结构设计及参数匹配[J]. 吉林大学学报:工学版,2012,42(5):1100-1106.

Wang Qingnian, Liu Songshan, Wang Weihua, et al. Structure design and parameter matching of ball-screw regenerative damper[J]. Journal of Jilin University:Engineering and Technology Edition, 2012, 42(5): 1100-1106. (in Chinese)

[11] Zhang Peisheng. Design of electromagnetic shock absorbers for energy harvesting from vehicle suspensions[D]. New York, USA: University of Stony Brook, 2010.

军队创新工程计划项目

2015-08-20；

2015-11-20

TM153; TB126; TH11