基于三坐标测量机的采样点数及其分布策略研究

苏长青，孙业翔，屈力刚，叶柏超，陈靖乐（.沈阳航空航天大学安全工程学院，辽宁沈阳036；.沈阳航空航天大学航空制造工艺数字化国防重点学科实验室，辽宁沈阳036）

基于三坐标测量机的采样点数及其分布策略研究

苏长青1，孙业翔2，屈力刚2，叶柏超2，陈靖乐2
（1.沈阳航空航天大学安全工程学院，辽宁沈阳110136；2.沈阳航空航天大学航空制造工艺数字化国防重点学科实验室，辽宁沈阳110136）

在测量过程中，圆柱度是经常需要测量及评价的形状误差参数，测量点数的选取会对其测量精度和测量成本造成一定的影响.综合考虑了径向谐波误差、轴向误差、特征尺寸、特征形状位置等影响测量结果的因素，提出了一种测量时确定采样点数的公式，并应用Hamme rsley序列、Halton序列、叶序理论来确定其坐标分布情况.在测量机中进行了实际测量，结果表明，结合3种成熟的布点策略，利用所提出的公式得到的采样精度均高于测量机自身软件的采样精度.

圆柱度；采样点数公式；分布策略；采样精度

随着现代制造业的飞速发展，人们对零件精度的要求越来越高，质量检验作为产品制造的“眼睛”，成为工业生产中极为重要的一环.三坐标测量机已成为质量检测环节中至关重要的设备，它不仅可用于评价零件的尺寸公差、形状误差和位置误差，还可以与上游设计、制造环节实现数据传递和数字驱动的基于MB D的数字化检测，形成设计、制造、检测的数字化闭环控制系统［1］.

三坐标测量机通过在产品上自动或半自动地采集测量点，利用测量软件算法来进行误差计算，测量结果主要由测量点的数量及其分布情况来决定.一些学者在研究了G P S（几何产品技术规范）的基础上，提出了一种新的基于特征的采样策略，完善了现有的评价标准.他们根据具体的圆柱特征，提出了采样密度与采样频率的概念［2-3］.这种方法的优点是方法简单，便于工程实现，但也存在着布点策略单一，测量精度偏低的不足.另一些学者则是在研究了实际零件的误差来源和精度影响因素的基础上，利用采样定理和谐波分析等方法研究了测量点数与测量精度的关系［4］.这种方法的优点是测量精度高，布点策略较为灵活，但算法较复杂，测量效率较低.

三坐标测量机对圆柱度误差进行测量时，会采用分层布点的方式，而分层布点后的采样点不能同时满足径向圆度和轴向直线度的测量精度和效率要求.针对此问题，本文提出了一种确定采样点数的数学模型，综合考虑了轴向采样点和径向采样点，并基于Hammersley序列、Halton序列及叶序理论确定了采样点的分布，较好地克服了测量机自身软件采样的缺点，为圆柱度测量时采样点的选取提供了新的思路.

1　测量点数的数学模型

1.1径向采样点数的确定

目前国内外公认的采样点数确定依据是Nyquist采样定理［5］.在实际测量过程中，圆柱的径向误差是由被测表面轮廓的极值点来决定的，故在测量时采样点应尽量接近这些极值点.

图1　采样周期与极值点位置的关系Fig.1Relation of sampling period and the extreme value point position

如图1所示，首先考察第一极值点A附近采样情况.假设在被测圆柱表面一个谐波变化周期内采样N个点（N≥2），谐波幅值为Cm，则采样点位置变化最大值为2π/N［6-7］.从E点开始采样，且A点落在δ和δ+1之间（δ=1，2，3，…，N），则δ点处采样值与极值点A处采样值之差为：

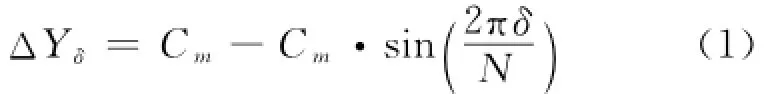
δ+1点采样值与A处采样值之差为：

但在实际测量过程中，采样点的位置是随机的，设采样点实际位置与理论位置的偏差为ΔX，为消除测量误差ΔX，设ΔYδ与ΔYδ+1相等，则：

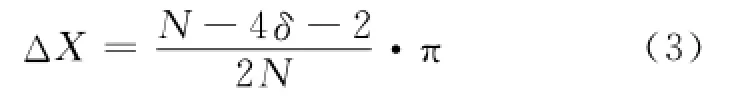
此时极值点A处附近的测量极限误差为：

同理可得第二极值点B处的测量极限误差为：

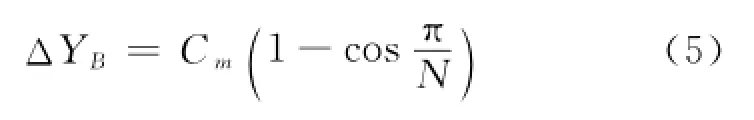
因此圆柱径向圆度的测量极限误差为：

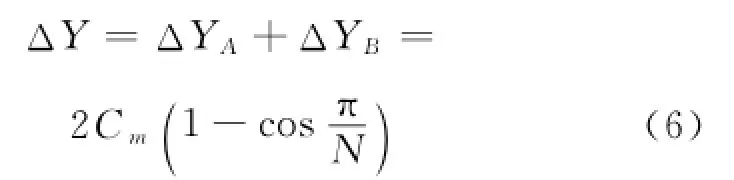
1.2轴向采样点数的确定

在轴向采样的过程中，为保证圆柱素线和轴线采样精度要求，采样时应考虑以下几方面因素：

（1）圆柱的长径比.设圆柱的长径比为i，当i ＞1时，圆柱素线与轴线之间的平行度公差值必须相应大于其圆度公差值；当i≤1时，圆柱素线与轴线之间的平行度公差值必须相应小于等于其圆度公差值.

（2）圆柱的柱面面积.在圆柱轴向采样时，圆柱面的面积也是需要考虑的主要因素之一.圆柱的柱面面积越大，为保证采样精度，则单位面积所需采样点数越多.设圆柱的柱面面积为S，则S =πDH.

（3）测量机测针红宝石球直径d.测量机在测量零件时，测头传感器记录的是红宝石球的球心位置，因此在无工装的情况下，测量的有效范围P=H-，如图2b所示.因此红宝石球直径越大，测量机的2有效测量范围就越小.当工装对其测量范围无影响时，则测量机的有效测量范围如图2a所示.

图2　测量机有效测量范围Fig.2Effective measurement range of coordinate measuring machine

综上所述，圆柱的径向采样点数N1与圆柱长径比i、圆柱表面积S、测针红宝石球直径d之间的关系为：

圆柱素线的直线度也是圆柱轴向误差的主要影响因素，如图3所示.由前述分析可知其测量精度要求和测量点数满足下列公式［8］：

式中：Δ Y为理论直线度误差；Cm为误差谐波分量最大振幅；M为在最大谐波分量下一个周期内的采样点数.

式中：N2为在整个测量行程内所需测量点数；K为获得最大谐波分量的谐波次数.

图3　圆柱素线直线度示意图Fig.3Schematic diagram of straightness of cylindrical generatrix

假设特征尺寸因素与特征形位因素对轴向采样精度的影响程度相同，则式（10）即为轴向采样点数公式：

1.3圆柱总采样点数

设圆柱总采样点数为N；轴向采样点数为N轴，轴向误差对圆柱度影响因数为φ1；径向采样点数为N径，径向误差对圆柱度影响因数为φ2，则圆柱总采样点数为：

φ1和φ2的选取与轴向公差、径向公差对圆柱度的影响程度有关，选取原则为：

（1）当轴向公差大于径向公差时，轴向公差对圆柱度误差的影响程度高于径向公差，应选取φ1＞φ2.

（2）当轴向公差小于径向公差时，轴向公差对圆柱度误差的影响程度小于等于径向公差，应选取φ1≤φ2.

2测量点的布置策略

2.1Hammersley序列及Halton序列布点

对于每个非负整数k和素数p，定义［9］：

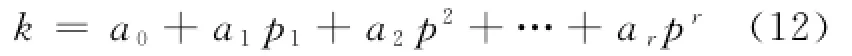
其中：ai∈［0，p-1］.

定义方程φp（k）为：

由式（12），（13）可推得：φp（k）∈［0，1］.

在d维采样空间中，设由互异的素数序列p1，p2，p3，…，pd-1定义序列φp1（k），φp2（k），φp3（k），…，φpd-1（k），第k个点的Hammersley序列为：

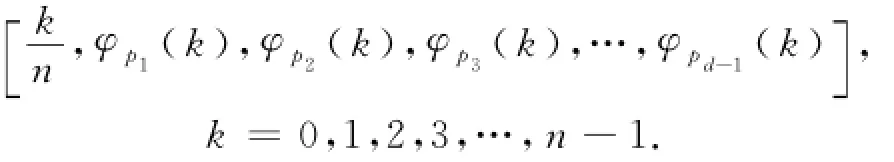
在Hammersley序列中，将第一项k/n去除后剩下项的集合即为Halton序列［10］.

2.2叶序理论布点

叶序理论是以斐波那契数列为基础来研究植物叶片沿径向排布情况的一种理论，其特点就是测量点按照叶序分布，其表达式为［11］：

φ=n·α，ρ=R，H=h·n（14）

式中：n为圆柱表面上点的序数；（ρ，φ，H）为第n个点的柱坐标；α为序数相邻两点之间的发散角；h为沿圆柱轴向测量的序数相邻两点之间的垂直距离.

3　试验验证

应用海克斯康HEXAGON-GLBALPERFORMANCE测量机，如图4所示；选取红宝石球直径为4mm的测针对φ=15，H=20的待测特征进行测量，测量情况如图5所示；测量结果如表1所示.

由表1可知，当K=2时，径向谐波幅值C2= 0.162773，将C2与精度要求ΔY=0.1mm代入式（6）中，可得在整个测量行程内径向测量点数为N径=KM=2×3.9=7.8，故可取N径=8.同理可得精度要求ΔY=0.05mm，圆柱轴向在整个测量行程内的测量点数N2=KM=1×3=3.

将待测圆柱的长径比i，侧面积S，红宝石球直径d代入式（7）中可得N1=10.23.将N1和N2代入式（10）中，可得轴线方向所需的测量采样点数（11）中，即可得到圆柱在测量时所需要的总的测量采样点数.根据φ1和φ2的选取原则，可取φ1=2，φ2=1.5，故圆柱所需总的测量点数为26个.

表1　径向和轴向各次谐波幅值Tab.1Every harmonic amplitude of radial and axial directions

图4　测量设备与试件Fig.4Measuring equipment and experimental part

图5　测量点分布示意图Fig.5Schematic diagram of measuring point distribution

在待测圆柱上分别采用Hammersley序列、Halton序列、叶序理论进行测量点的布置，选取测量点数为10，15，20，25，26，30，35，40，45，50个时测量机所测得的圆柱度误差如图6和表2所示.

图6　各布点方法圆柱度误差测量结果的比较Fig.6Comparison of measurements results using different sampling methods

表2　不同布点方式在三坐标测量机中圆柱度误差的测量结果Tab.2Measurement results of coordinate measuring machine using different sampling methods

4　结语

（1）圆柱采样点公式为N=φ1N轴+φ2N径，其中φ1，φ2分别为轴向和径向精度要求对采样点数的影响程度.

（2）按照H ammersley序列、Halton序列及叶序理论进行测量点的布置时，采样精度均高于测量软件的布点策略.

（3）本文所提出的数学模型适用于大量同批次零件检测时测量点的选取，可明显提高批量检测的效率和准确性.

［1］ 张国雄.三坐标测量机的发展趋势［J］.中国机械工程，2000，11（1/2）：222-226.

ZHANG Guoxiong.The development tendency of coordinate measuring machines［J］.China Mechanical Engineering，2000，11（1/2）：222-226.

［2］ 张琳娜，郑玉花，郑鹏.基于G P S的提取操作模型及其应用规范研究［J］.机械强度，2007，29（4）：632-636.

ZHANG Linna，ZHENG Yuhua，ZHENG Peng.Model of extraction operation and the research of it’s application specification based on GPS［J］.Journal of Mechanical Strength，2007，29（4）：632-636.

［3］ 郑鹏，张琳娜，陈明仪.现行圆柱度测量方法分析及采样方案新策略［J］.机械强度，2011，33（1）：152-158.

ZHENG Peng，ZHANG Linna，CHEN Mingyi.Analysis of current cylindricity measurement method and new sampling strategy［J］.Journal of Mechanical Strength，2011，33（1）：152-158.

［4］ 陈隆德，王锡琨，王振明.圆度误差测且中测点数的确定［J］.大连理工大学学报，1990，30（3）：307-400.

CHEN Longde， WANG Xikun， WANG Zhenming.Determining points number for measurement of circularity error［J］.Journal of Dalian University of Technology，1990， 30（3）：307-400.

［5］ 金伟.现代检测技术［M］.3版.北京：北京邮电大学出版社，2012.

JIN Wei.Modern detection techniques［M］.3th ed.Beijing：Beijing University of Posts and Telecommunications Publishing House，2012.

［6］ 张凤翔，赵辉.直线度测量中采样间距与偏差形状关系的理论研究［J］.航空计测技术，1995，12（2）：9-13.

ZHANG Fengxiang，ZHAO Hui.Theory research between sample step and deviation shape in linearty measurement［J］.Aviation Metrology & Measurement Technology，1995，12（2）：9-13.

［7］ 林家风，顾伯达.圆度误差的富里叶分析［J］.武汉工学院学报，1990，12（1）：24-31.

LIN Jiafeng，GU Boda.Fourier analysis of roundness error［J］.Journal of Wuhan Institute of Technology，1990，12（1）：24-31.

［8］ 董玉德，汪玉玺，刘达新，等.三角平面Halton点采样策略及其性能分析［J］.计算机辅助设计与图形学学报，2007，19（8）：1063-1068.

DONG Yude，WANG Yuxi，LIU Daxin，et al.Halton points sampling strategy and performance analysis for triangle plane［J］.Journal of Computer-Aided Design & Computer Graphics，2007，19（8）：1063-1068.

［9］ WONG Tientsin， LUK Waishing， HENG Phengann.Sampling with hammersley and halton points［J］.Journal ofGraphics Tools，1997，2（2）：9-24.

［10］ LEE G，MOU J，SHEN Y.Sampling strategy design for dimensional measurement of geometric feature using coordinate measuring machine［J］.International Journal ofMachine Tools and Manufacture，1996，37（7）：917-934.

［11］van ITERSON G. Mathematische und mikroskopishanatomische studien iiuber blattstel Lungen［M］.Jena： Gustav Fischer，1907.

Sampling points and distribution strategy for coordinate measuring machines

SUChang-qing1，SUNYe-xiang2，QULi-gang2，YEBai-chao2，CHENJing-le2
（1.School of Safety Engineering，Shenyang Aerospace University，Shenyang 110136，China；2.Key Laboratory of Fundamental Science for National Defense of Aeronautical Digital Manufacturring Process，Shenyang Aerospace University，Shenyang 110136，China）

Due that the cylindricity is frequently used as a measurement and evaluation parameter for shape error，the number selection of measurement points impacts the measurement precision and cost.By comprehensively considering such impact factors as radial harmonic error，axial error，feature size，feature shape location，a formula is proposed to determine sampling points.The coordinate distribution is obtained using the Hammersley sequence，Halton sequence and phyllotaxis theories.With practical measurement on measuring machine，it is indicated that the sampling precision with integration of three stationing strategies is higher than the attached software of measuring machine

cylindricity；sampling point number formula；distribution strategy；sampling precision

T P 391.7；TH 721

A

1672-5581（2015）06-0566-05

苏长青（1979-），男，副教授，硕士生导师，博士后.主要研究方向为机械系统可靠性及优化设计、复杂结构系统模拟仿真、数字化检测技术.E-mail：sucq@sau.edu.cn