刍议“构造法”在中学数学教学中的应用

☉江苏省南京市金陵中学 严 飞

现今的高中生数学的学习偏重于演绎推理的训练，过分强调形式论证的严密逻辑性，忽视数学知识形成、发生、发展过程中生动活泼的一面，以及包含着大量的可进行创造性理解的素材，把数学思维能力的培养基本上局限于逻辑推理上，无形中造成了对数学思维的偏见，这不仅不利于数学创造性思维能力的培养，而且也削弱了数学教学的作用.数学不但要培养学生的思维能力，还要培养学生的数学素质，培养学生灵活运用知识的能力，培养学生的创造性思维能力.高中数学的构造法是一种培养学生创造性思维的教学方法.构造法的内容十分丰富，形式多样.它主要将数学中普遍性与现实性的问题特殊化，抽象性的问题实质化，并根据具体的数学问题采取相应的解决办法，进而激发学生的学习热情.

一、高中数学构造式解题教学应遵循的原则

（一）要求通过构造教学模式将所要解决的数学问题的本质形象直观地显示出来，缩短学生的思维过程，引导学生逐步建立模式识别的方法，提高教学效率.

（二）在教师的引导下使学生能够顺利实现问题的转化，创设的问题符合学生的认知水平，提高学生的解题能力.

（三）合理运用直觉、化归等方式，找到问题的“相似结构”的原型，对现有问题进行联想并作出判断，从综合分析层面引导学生解决数学难题.

二、高中数学构造式解题教学培养学生创造性思维能力的途径

通过构造教学模式培养学生的创造性思维能力的途径有：（1）深入观察，洞察实质；（2）善于联想，促进迁移；（3）着意类比，启发直觉；（4）纵横延伸，广泛联系.

1.构造时深入观察，洞察实质

仔细观察问题，有可能发现问题的突破口，想出某种解决问题的方法.对某些数学问题，观察题设和结论的结构、解析式或图形的变化规律、题目所给出的数据关系等显信息，以及问题所联系的背景知识和隐含条件等隐信息，有利于洞察数量关系和结构关系，进行跳跃性思维，缩减某些推理环节，增强直觉意识，为创造思维能力的发挥奠定基础.

（1）构造函数与方程.

用构造方程法解题培养学生的观察能力是一种新型的教学理念，因为方程是学生解题中最常用的模式，也是学生如何将新的问题化归为已学知识的一种途径，这将有助于培养学生的直观思维能力.方程与函数有必然的联系，是数学的两种解题形式.例如，函数y＝f（x）的图像与x轴的交点的横坐标就是方程f（x）＝0的解.在解数学题时，若要确定函数中变化的某些量，可以将其转化为求出这些量满足的方程，通过构造函数图像将要解决的函数问题形象地展现出来，然后解方程得到最终解，提高解题效率.

（2）构造几何图形.

我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事非.”数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”，即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的.

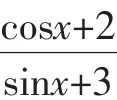
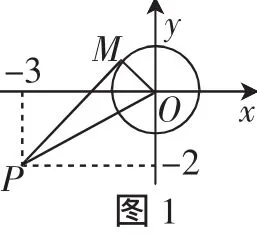
分析： 从函数的表达式上来看，函数（fx）的几何意义是：单位圆上的点M与定点P（-3，-2）的连线的斜率.如图1，设单位圆x2+y2=1过定点P（-3，-2）的切线PM的斜率为k，则切线PM的方程为y+2=k（x+3），即kx-y+3k-2=0.

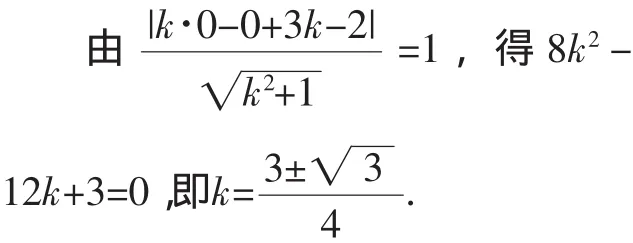
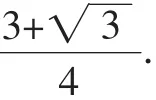
（3）构造新数列.

在高中数学中，数列的通项公式的求法有多种，但利用构造新数列把非特殊数列转化为等差、等比两种典型的特殊数列是最为重要的.构造新数列需要比较灵活的变形技巧，可以培养学生的创新能力.

例3 设数列{an}的前n项和为Sn.已知a1=a，an+1=Sn+3n，n∈N*，求数列{an}的通项公式.

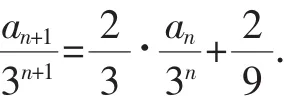
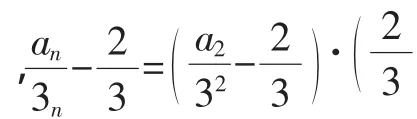
故数列{an}的通项公式为：

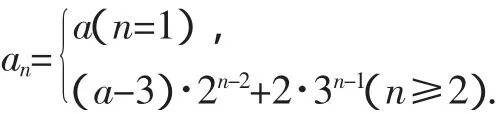
求由an=pan-1+f（n）·rn确定的数列的通项公式，一般可以通过左右两边同除以rn，消除不和谐的rn.

2.构造时善于联想，促进迁移

联想是由此及彼的思考方法.联想要以一定的数学知识、解题经验及技能为基础.对于某些数学问题，若能联想一些形式相同的、思考方法相似的、结构类似的数学问题或常规问题，通过迁移将会悟出解决问题的思路.心理学家认为：把不同事物联系起来思考，是人类进行创造性思维活动的重要形式.创造性联想就是由一个事物联想到另一个事物的思维过程.各种不同属性的事物反映在头脑中，并形成了各种不同的联想.常见的联想方式有：类比联想、相似联想、对比联想、化归联想、属性联想、反向联想和因果联想等.联想是创造性思维的一种常用思考方法.

例4 求函数y=的最小值.

分析：若用代数方法求解本题，较难入手.

思路1：联想到两点间的距离公式，将函数解析式改写为y=，则此函数表达式的几何意义是x轴上的动点P（x，0）到两定点A（4，1）、B（-2，-5）的距离之和，而A、B分布于x轴的上下两侧，则ymin=|AB|=

思路2：联想到向量，构造向量.

设a=（4-x，1），b=（x+2，5），则a+b=（6，6）.

根据向量不等式|a|+|b|≥|a+b|，得y=

3.构造时着意类比，启发直觉

类比是一种推理形式，是联想的一种特殊形式和常用的推理方法.类比的具体形式有：问题形式类比（提出新问题）、结构类比（发现新解法）等.通过类比，调动大脑中贮存的信息，进行知识组块，启迪思维，出现“顿悟”，顿悟的出现是解决问题的关键，顿悟是创造性思维的一种表现形式.数学研究的对象主要是数和形，两者往往有着紧密的联系.俗话说：“数离形时少直观，形离数时难入微”.因此，对数学问题的直观理解是非常重要的.引导学生通过深入的观察、联想，由形思数，由数想形，利用数形直观诱发直觉，对培养直觉思维的敏感性和提高其准确性，对诱发创造性思维的产生，大有益处.

例如，函数的单调性与函数的奇偶性是函数的两个最基本的性质，将这两个性质结合起来研究，学生都能理解：若函数f（x）是偶函数，且f（x）在x≥0时是单调增（减）函数，则函数f（x）在x≤0时是单调减（增）函数，即偶函数在对称轴的两侧有相反的单调性.通过观察函数f（x）=x2的图像，可以发现函数f（x）=x2的图像的形状像一个喇叭，像这样的函数，我们不妨形象地给它一个名字——“喇叭型函数”.“喇叭型函数”的特点是：函数的图形有对称轴，在对称轴的两侧函数有相反的单调性.不难证明，满足f（a-x）=f（a+x），且在x≥a时单调的函数f（x）是“喇叭型函数”.当“喇叭”的开口向上（左减右增）时，距对称轴距离相等的点纵坐标相等，即函数值相等；距对称轴距离大的点纵坐标也大，即函数值也大；距对称轴距离小的点纵坐标也小，即函数值也小.反之，当“喇叭”的开口向下（左增右减）时，距对称轴距离相等的点纵坐标相等，即函数值相等；距对称轴距离大的点纵坐标却小，即函数值小；距对称轴距离越小的点纵坐标却大，即函数值大（如图2所示）.

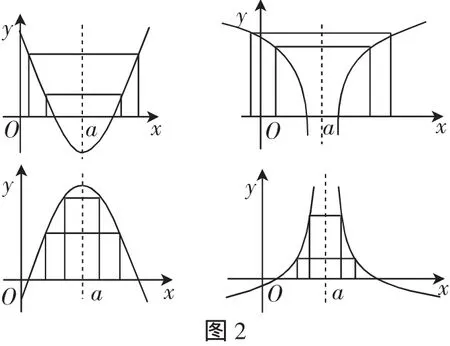
4.构造时纵横延伸，广泛联系

知识的更新和扩充，在于对所学知识的延伸，在于当前知识与已学知识的广泛联系.构造教学中应引导学生在更广、更深的领域内挖掘知识的内在联系，探究问题的纵横延伸，从而在实施转化的过程中培养学生思维的广阔性，达到培养学生创造性思维的目的.

例5 当0＜a＜1时，试判断sin（1+a）与sin（1-a）的大小.

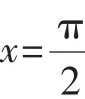
这样，代数函数的性质在三角函数的领域内就有了应用的可能，既体现了知识的系统性，又培养了学生的扩散思维，使学生尝到了创造的滋味，亲身体验到了创造的意义，使创造性思维的形成成为可能，以致必然.

三、高中数学构造式解题教学应避免为讲构造法而人为构造

在教学中对学生的思维能力应有正确的认识，用构造法要达到化繁为简、化难为易的目的，应避免在教学时为了讲构造法而人为构造，增加学生对数学的畏惧感和挫折感.

例6 设a、b、c是三角形的三边长，证明不等式2（ab+bc+ac）＞a2+b2+c2.

用构造法证明：因为a、b、c是三角形的三边长，所以a＜b+c，b＜a+c，c＜a+b.不妨设0＜a≤b≤c＜a+b，则a＜4b.

令（fc）=c2-2（a+b）c+a2+b2-2ab（b≤c＜a+b）.

则f（b）=b2-2（a+b）b+a2+b2-2ab=a2-4ab=a（a-4b）＜0.

又因为y=f（c）为开口向上的抛物线，且a+b为抛物线的顶点的横坐标，所以当b≤c＜a+b时，恒有f（c）＜0，即c2-2（a+b）c+a2+b2-2ab＜0，所以2（ab+bc+ac）＞a2+b2+c2.

本题一经构造反而让学生感觉数学深不可测，没有达到化繁为简的目的，反而让学生更糊涂了.事实上，由a、b、c是三角形的三边长，得到a+b＞c，a+c＞b，c+b＞a，且a＞0，b＞0，c＞0，于是有ac+bc＞c2，ab+bc＞b2，ac+ab＞a2，三式相加即得2（ab+bc+ac）＞a2+b2+c2.

四、结束语

有一些问题看似简单，但真正处理起来非难则繁，如能合理、巧妙地构造一些情境，不但易使问题“柳暗花明”，而且其新颖独特的解题模式让人深刻感受到数学思想的美妙.但我们的教学不应是在追求美妙上下功夫，更主要的是把解题用到的数学思想和方法介绍给学生.运用构造方法解题也是这样，不应为了讲解构造法而人为构造，更应启发学生从多角度、多渠道进行广泛的联想，从而获得许多构思巧妙、新颖独特、简捷有效的解题方法.通过解题活动加强学生对知识的理解，培养思维的灵活性，提高学生分析问题的创新能力.

1.单墫.普通高中课程标准实验教科书数学·选修2-1［M］.南京：江苏教育出版社，2012.

2.张定强，赵宏渊，杨红.高中生数学反思能力培养的基本模式与实践探索［J］.数学教育学报，2008（1）.

3.章建跃.中学数学课改的十个论题［J］.中学数学教学参考（上），2010（3）.

4.郭玉峰，史宁中.数学基本活动经验：提出、理解与实践［J］.中国教育学刊，2012（4）.

5.宋玉连.构造法在解题中的应用刍议［J］.连云港教育学院学报，1999（2）.

6.田发胜，例谈构造复数解题［J］.中学数学教与学，2000（9）.