“多想少算”思想下对立体几何问题的解答

☉江苏省江浦高级中学 刘金勇

对考生分析问题、解决问题能力的考查是高考重要考查点之一，考试说明中明确要求：解题中能选择有效的方法和手段对新颖的信息、情境和设问进行独立思考与探究，建设性地解决问题.本文以立体几何问题为例说明“多想少算”思想的运用，以期对同学们解题有所帮助.

一、构造特殊模型，化抽象为直观

例1 （2015年北京西城一模）如图1，四面体ABCD的一条棱长为x，其余棱长均为1，记四面体ABCD的体积为F（x），则函数F（x）的单调增区间是_____；最大值为______.

解：联想特殊几何模型，该四面体可视为菱形ACBD（其中∠CAD=60°）沿对角线CD折叠而成.

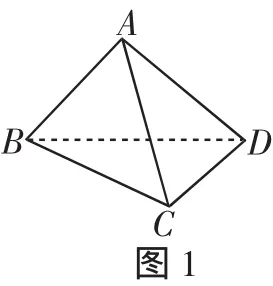
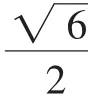
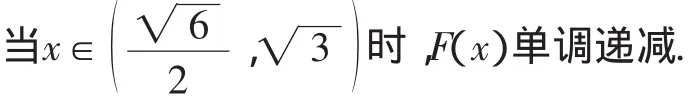
评析：本解法通过构造特殊模型，将复杂的运算孕于简单的推理之中，符合高考命题“小题小做”“多想少算”的理念.

二、还原于规则几何体，化隐为显

例2 如图2，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且△ADE、△BCF均为正三角形，EF∥AB，EF=2，则该多面体的体积为________.

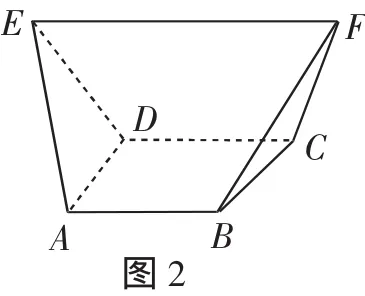
分析：由于本题中多面体ABCDEF为非规则几何体，不能直接求其体积，因此可以考虑用分割法，使其分割为两个体积相等的三棱锥与一个直三棱柱.

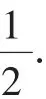
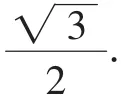
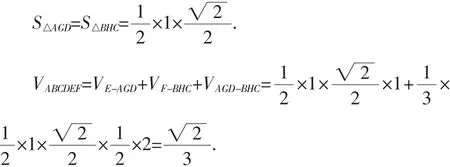
评析：某些问题中所给出的几何体虽然并不规则，但通过深思不难发现其都有规则之处，即这些几何体都可以视作由规则的几何体即长方体或正方体切割而得，进而使其隐含的性质得以直观体现，使问题简洁得解.

拓展：本题还可以这样来分割：取EF的中点P，则多面体ABCDEF分割成正四面体ADEP、正四面体PBCF和正四棱锥P-ABCD，也易于计算.

三、空间化平面，三维降二维

例3 如图3，一圆锥的底面半径为2，母线PB的长为6，D为PB的中点.一只蚂蚁从点A出发，沿着圆锥的侧面爬行到点D，则蚂蚁爬行的最短路程为（ ）.

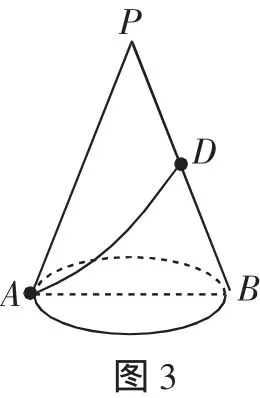
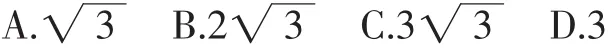
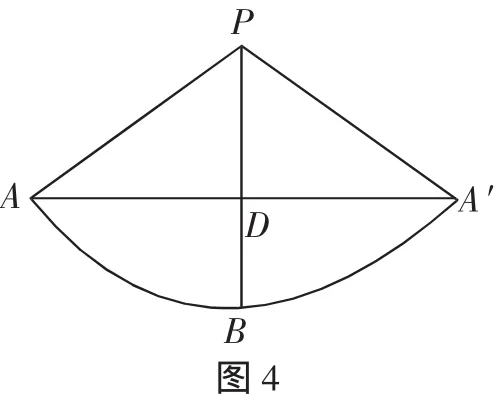
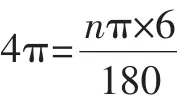
评析：对空间想象能力的考查，是考试大纲提出的对考生能力点的考查之一.圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形，“化曲面为平面”，用勾股定理解决.本解法将三维化二维，有效降低了对空间想象能力的要求，将几何量隐含的关系直观显现出来.

四、动中有静，寻找不变量

例4 如图5，在长方体ABCD-A1B1C1D1中，AB=4，BC=CC1=，M是BC1的中点，N是MC1的中点，若异面直线AN与CM所成的角为θ，距离为d，则dsinθ=__________.

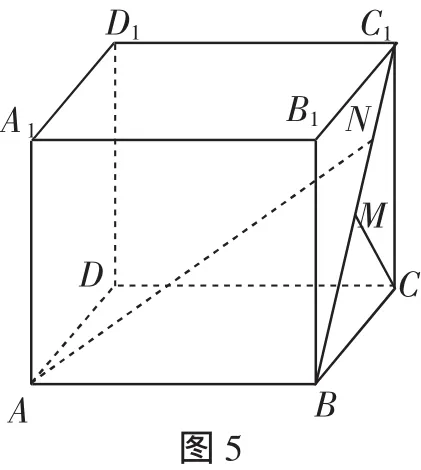
解：取CC1的中点K，则KN∥CM，故∠ANK为异面直线AN与CM所成的角或其补角.

因为AB⊥面BCC1B1，CM⊥BC1，所以CM⊥AN.又KN∥CM，所以KN⊥AN，即θ=90°.

因为CM∥KN，所以CM∥平面ANK，故异面直线AN与CM的距离等于直线CM与平面ANK的距离，即等于点M到平面ANK的距离.而平面AKN⊥平面BCC1，所以点M到平面ANK的距离等于点M到直线AN的距离.

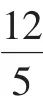
评析：长方体中不仅包含了所有的数学思想方法，密切了与中学数学中其他内容的联系，更体现着从静到动，从单一到多方面，从长方体本身应用问题到利用长方体去解决问题的发展变化.仔细研究这些变化对学好空间几何无疑是有裨益的.

五、化动为静，以直代曲

例5 如图6，已知正四棱锥V-ABCD可绕着AB任意旋转，AB⊂平面α.若AB=2，VA=，点V在平面α上的射影为O，则CO的最大值为______.

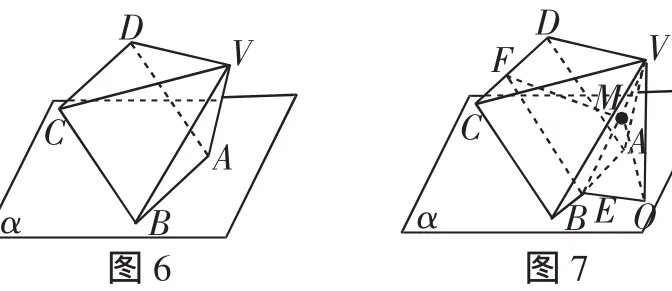
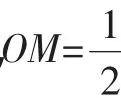
要求CO的最大值，可以转化为先求OF的最大值.

OC2=CF2+OF2≤CF2+（OM+MF）2=，当且仅当O、M、F三点共线时取到等号，所以CO的最大值为

评析：本题中除了固定不变的长度、线线、线面、面面关系外，还渗透了一些“动态”的点、线、面元素，给静态的立体几何题赋予了活力，使题意更加新颖，解法更加灵活，思维更加广阔.也正因为某些点、线、面位置的不确定，成为学生进行常规思考、转化的障碍；但又因为其是可变的、开放的，更有助于学生空间想象能力及综合能力的培养.只有多方着力，寻求转化，才能摸索出解决动态立体几何问题的基本策略.

综上，对学生数学解题能力的培养，是高中数学教学目标之一，教学中教师应注意从解题思路的寻找上多下功夫，如此题如何解，为什么这样解，这种解法是如何想到的等，建立知识间的有效关联，进而在解题中迅速寻找到简洁的解题途径.