润物细无声——谈数学教学中的思维训练
2015-08-27江苏省西亭高级中学
☉江苏省西亭高级中学 王 进
我们都听过一句名言:数学是思维的体操.其实这句名言最早是由十八世纪俄国元帅苏沃洛夫——一位军事家说的,后来不断被前苏联教育家引用至今.我们很纳闷:为什么这句话首先是一位军事家想到的呢?其实,在军事作战中不断需要使用各种思维辨解、判断,需要极强的逻辑分析能力,可以这么说,军事家都是不折不扣的数学大师.无独有偶,我国古代军事家孙子所著的《孙子兵法》正是对数学思维训练的一种体现!其虽然所讲的是对敌作战的用兵之道,但是也可以将它活用为教师对学生课堂思维训练培养之术,从“善战”与“谋略”巧妙地研究思维规律,到“知彼知己,百战不殆”与“待敌者佚”正确形成思维定势;从“深入则专,主人不克”进一步提高思维品质,将会出奇制胜,使学生越学越聪明,何乐而不为呢?
我们设计和组织的教学过程,不应该仅仅是传授知识、形成技能的教学过程,它应该是在进行“双基”教学的同时,既是学生学会学习的过程,又是开发智力、培养能力的过程,也是发展学生个性品质,给以教养的过程.因此,数学教学是思维活动的教学.那么如何在数学教学过程中提高思维品质、发展思维能力呢?笔者以孙子兵法之谋略结合案例给予说明.
一、“善战”与“谋略”研究思维规律,提高课堂教学质量
孙子曰:“见胜不过众人之所知,非善之善者也;战胜而天下曰善,非善之善者也.”孙子认为战争是一门复杂的综合艺术,它需要指挥员全面掌握战争取胜之道.苦战赢来的胜利,虽值得称道,但也难得称之为“善战”.所以真正“善战”者,必须是有较强的实力和充分的准备,且在知己知彼的情况下大获全胜.孙子揭示的这一现象,不仅是揭示战争的普遍规律,也是批判传统教学,重视了“双基”,重视了演绎论证能力的训练,这是必要的.但是现阶段数学教学,笔者也发现这样的现象:我们一直偏重知识性的训练、熟练程度的训练,却忽视对学生思维方向的训练,这也是受限于应试的影响.笔者始终认为:对学生思维的培养与应试不存在必然的不可兼得性,因为有了扎实的基本功,所以会追求更深层次的问题,必然加深学生对深层次问题的思考,促进了其思维的发展;反之,有了深刻思维的发展,使学生考虑问题的全面性、深刻性、反思性等都有了长足的进步,这也加深了学生对数学问题解决和应试的促进作用.
因此,“谋略”即要丰富联想,加强思维能力培养,为“善战”做准备.但必须提高认识:现阶段数学教学是一种思维化的教学活动,在这样的教学活动中要努力提高学生数学思维的可塑性,加强知识发生、整合、发展、联系的全过程.那么思维的过程是怎样进行的呢?笔者以解题为例,做简单剖析.
案例1:求函数y=2sin2x+sin2x的值域.
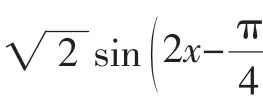
孙子曰:“夫未战而庙算胜者,得算多也;未战而庙算不胜者,得算少也.多算胜,少算不胜,而况于无算乎.吾以此观之,胜负见矣.”孙子主要讲的是“谋略”,其强调的是战争前的预测,强调对敌情的判断,不对战情进行预测,不对战情加以了解,一般不可能取得胜利.由此笔者分析上述解题的思考过程,经过审题,我们同时从题给条件和结论中获得有关信息——条件信息和目标信息.在获得信息的过程中,“联想”(即“谋略”)已经在起作用:数学符号和数学概念的相互转化和翻译;由条件信息进一步发散众多的结果,这里联想又一次起作用:由有关数学概念和性质,推导、演变出更多的结果;条件信息和目标信息联系起来思考,初步设想解题方向,我们称之为思维定向(即“吾以此观之,胜负见矣”),这里更离不开丰富的联想(即“谋略”).可以将从孙子用兵中得到的解决问题的数学思维活动用框图表示如下:
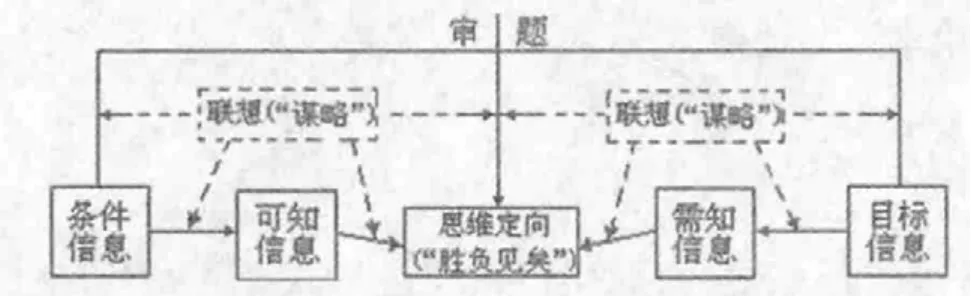
可以这么说,在解题过程中思维的定向并不见得一次完成,它往往是由大到小,由粗到细,逐步完成的.从上述思维过程的分析可以看出:联想(即“谋略”)在思维活动中占据着重要的地位.
二、“知彼知己,百战不殆”与“待敌者佚”形成思维定势,发展思维能力
人们的思维活动离不开丰富的联想.当一个学生获得信息之后,能否产生丰富的广阔的联想,一是取决于该学生大脑中储存的思维定势的质量,二是取决于该学生的思维品质,特别是思维的深刻性和灵活性.
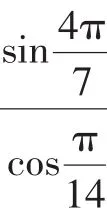
孙之曰:“知彼知己,百战不殆;不知彼而知己,一胜一负;不知彼,不知己,每战必殆”,即了解敌人,又了解自己,百战都不会有任何危险.因此,如果在教学中,概念一带而过,结论和盘拖出,靠反复练习建立“条件反射”,这种条件反射式形成的思维定势,就容易起负迁移的作用,即形成不知彼而知己.相反地,在教学中如果注意知识发生过程的教学,使学生在积极参加思维活动中,尽可能主动地获得思维的成果——概念、公式、定理等,这样形成的思维定势,就能较好地起正迁移作用,即知己知彼,对整个知识体系的形成过程了如指掌,运用自如,百战而不殆.
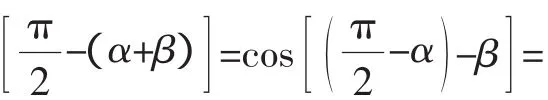
这个结果也很漂亮.只不过书本上并没有把它作为公式.因此,不要把教学停留在抠题型、对套路,只讲小巧、不要大巧的讲解解题术的水平上,企图通过强化解题模式,形成众多的定势来对付考试,会破坏人的灵感,使人呆板.当然,数学离不开做题.加深概念的理解,领会公式的实质,都要通过反复练习来进行.但是思维的问题是一个教师如何教,怎样讲,不能仅限于大量试题的重复训练.
三、润物细无声般渗透思维训练
上述谈到怎么教,怎么讲,笔者认为,通过数学试题去渗透思维训练需要一种多角度,并且是慢调细语式的训练.心理学家德诺普说过:对于思维训练,从心理认知来看,是一种新、旧知识的碰撞和冲突,当这种冲突渐渐向旧知靠拢时,思维的含量就渐渐被提升起来,但是这种过程必须是依赖受教者自身不断的认知基础,外界强加的力量并不能使其真正领悟.因此,笔者认为润物细无声般的渗透是对思维训练比较好的方式,这需要教师提供足够的思考空间和时间.
案例3:高一学生解一元二次方程时,教师会涉及换元法.精选出一组例题,解下列方程:
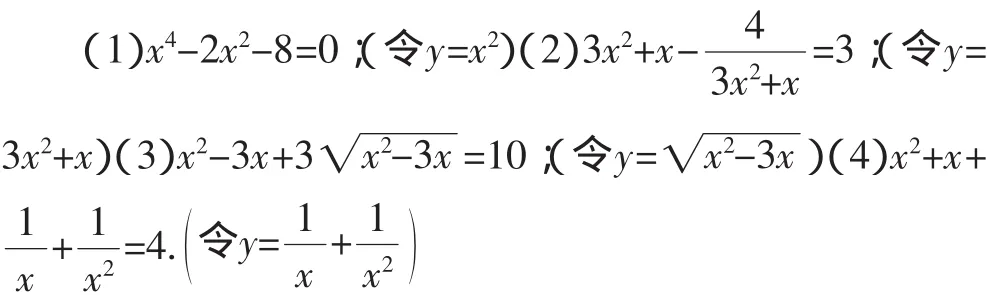
一种教法是一道道地讲授如何通过换元把它们转化为一元二次方程求解,然后总结:“凡是遇到无理方程、倒数方程,可以考虑用换元法.”但笔者认为,要培训思维,可以采用另一种教法即“奇道”.
师:同学们看看方程(1),这是个什么方程?
生1:一元四次方程.
师:我们学过这样的方程的解法吗?我们会解哪些方程?
生2:我们学过一元一次方程、一元二次方程和二元一次方程组的解法.
师:那么怎么解这个四次方程?
生3:想办法变成我们会解的方程就好了.
师:同学们看看方程(1),在构造上有什么特点(将方程(1)写成:(x2)2-2(x2)-8=0).
生4:可以把x2看成一个未知量y,即令y=x2,方程可以变成一元二次方程y2-2y-8=0.
师:四次方程虽然没有学,我们注意到它构造的特殊性——双二次结构,于是可采用变量替换的办法,即用换元法将它化成我们熟悉的一元二次方程来解决.利用类似的思想和方法,大家能不能解方程(2)、(3)、(4)呢?(此处不赘述)
师:这些方程的解决都是借助换元法.同学们想一想:为什么要换元?换元有什么好处?
生5:通过换元,把生疏的方程转化为我们熟悉的一元二次方程,从而能够解出这些方程.
师:换元法即通过变量替换,达到化繁为简、化“生”为“熟”的目的.这种转化问题的思想、化归的意识是我们处理问题的常用数学思维.
对于思维训练,正如后一种教师的教法,使学生体会到为什么要用换元法,使用换元法的好处是什么.其思维最大训练正是体现了数学中最重要的思想——转化与化归思想.
总之,本文用于无声处听惊雷的方式阐述了思维训练的几个方式.既讲了问题解决的方向性策略,又引导了思维训练中定势思维在解决一般性问题中的用处,结合案例做了一些浅显的分析,不足之处请读者海涵.
1.方明.陶行知教育名篇[M].北京:教育科学出版社,2005.
2.姜兴荣.探求解题思路的几种有效策略[J].中小学数学,2013(7-8).
3.朱永祥.再谈数学思想方法的挖掘和应用[J].中学数学(上),2008(2).
