透视问题本质 培养解决能力
2015-08-27江苏省海安县曲塘中学王正余
☉江苏省海安县曲塘中学 王正余
数学教学的最终目的是要培养学生解决问题的能力.波利亚在解题中谈到:“提高学生问题解决能力的关键是让学生能够清晰地透视问题的本质!问题的本质是如何找到的?那就离不开三件事,其一是分析问题,即对问题进行解剖,了解条件和所需结论之间的关系和链接,找到一个或多个突破口进行尝试;其二是透视本质,即在分析问题的基础上找到问题的本质,站在更高的地方来看问题解决需要联系的数学知识和解决方法,能够想到存储在脑海中最基本的数学知识和基本技能;最后是转化解决问题,即将陌生问题进行合理的转化划归,每一个陌生的数学问题都需要转化为熟悉的模式进行求解.”波利亚的解题经验告诉我们,数学问题解决的三个步骤.在三个步骤中,笔者认为最重要的是第二个环节,即如何解剖问题,认知问题的本质!
华师大张奠宙教授说起过一个解题的案例,让人忍俊不禁:一个三层饭店的电线坏了,因为电工请假几天,于是大家束手无策暂时查不出哪里出了问题,于是用电源器械一个一个的试,终于找到了问题,只不过花了半天时间.其实,若电工查只需要用欧姆表将导线之间连接,看线路的电阻值就可以查询问题,区区几分钟就可以解决.这个案例告诉我们,电工知道反应电路问题最本质的原因,而门外汉自然是只能用穷举的方式来解决问题.笔者认为,这正是我们学生对于现阶段数学学习问题解决中出现的情况类似,下文笔者谈谈如何透视问题本质,培养问题解决能力.
一、通过模式识别透视本质
模式识别是数学解题教学中最基本的运用,高考问题的解决也是对学生进行长时间的模拟训练,模式识别是操作后进行的应试.北师大张英伯教授就模式识别的优点进行过指出:“模式识别是中学数学解题教学中比较高效有效的模式,它把学生对于数学知识将面临的问题考向进行了甄别和归类,对于形式化思维比较弱的中学生而言是有好处的,也有利于应试稳定性.”比如,高中数学中的解析几何一章,是模式识别观察问题本质较为显著的章节.笔者思考:解析几何问题很少用来压轴,为什么?正是因为其问题本质通过模式识别容易掌握,思维考查量不大,其最难的部分来源于数学运算能力的考查,因此解析几何问题的本质是比较容易把握的,解析几何问题解决能力是可以通过训练得到提升的.
具体谈谈解析几何,在解析几何一章的教学中,一类重点、难点同时也是考试热点的就是直线与圆锥曲线的位置关系.这类问题的解决往往有一个固定的套路,那就是联立直线与圆锥曲线方程,消元后使用判别式、韦达定理等工具.但是这类问题传统解法的一个最大特点是运算量比较大,而且一般还综合一个或更多的字母参数,所以学生对这类题特别“感冒”,然后就寻思着特殊方法和技巧,一心想走捷径.针对这种现象,笔者采取的招数是让他们“打擂台”:女生用常规的套路演算,男生则找捷径,让他们尝到“绞尽脑汁,伤透脑筋”,最终以失败而告终的苦果.
教师:这是一道高考改编题,主要是对于直线和圆锥曲线位置关系的考查.
学生众:(很关注,迫不及待的神情)读题.
教师:很经典的问法,很古老的问题:直线过定点.
学生众:有些失望.
教师:很明显我们应该先求出直线MN的方程.
学生众:更大的失望.
学生A:(与同桌窃窃私语)这样的问题似乎有些陈旧,不新鲜.
教师:(看到这种形势,又听到学生A的这句话,话锋一转)有的同学轻视老一套,总想走捷径.俗话说得好,“条条大路通罗马”.我们今天就来一个老题新解法,比比谁先到罗马.咱们女同学吃点亏,踏踏实实走老路,男同学好好发挥你们的智慧,找找捷径试试看.
学生众:顿时气氛又高涨起来.女同学忙碌着,男同学有画图的,有凝神苦思的,有紧锁双眉的……(时间在一分一秒地过去,沙沙声不绝于耳)
学生C(男生):啊!还没有解答完毕!
教师:感觉怎样?
学生D(女生):运算是繁了一些,但是很有效.
教师:遇到问题多问一个为什么,试着多找几条路是应该的,但过分追求就等于舍本逐末.而考试又是在规定时间内解题,所以捷径在有限的时间内一旦难于寻找,不妨回到最基本的方式.总之,还是这句话,要重视通性通法(即解析几何问题最一般的模式处理方式).
说明:解析几何问题最根本的处理方式自然是联立直线和圆锥曲线方程,利用题中条件,解决直线方程,解决直线过定点.解析几何问题最难的并不是思维方式,而是在合理的模式识别中进行正确的代数运算,以及保持清醒的计算头脑、长时间训练的熟练程度,正是有了这样的问题本质的透视,才能给解析几何问题的解决带来更高的效率.
二、通过知识积累透视本质
知识重在积累、重在经验.我们知道教材中有很多概念、性质、定理,但是用这些来解决问题还不够,现阶段的应试还需要对于知识本质的理解和熟练.大量调查研究表明,要在中学应试中取得较为优秀的成绩,仅理解数学概念、性质是远远不够的.还需要对于很多知识进行额外的积累.以数学为例,我们都知道等差数列最基本的通项公式和求和公式,但是学生对于等差数列的认知却仅限于这几个基本公式,很多学生并不知道数列是一种特殊的函数,也没将等差通项公式的函数本质和求和公式的函数本质进行知识的积累(教材中并未对这些公式进行函数本质的挖掘),因此,需要不断积累增强问题理解的本质,进行培养问题解决的能力.
案例2:关于等差数列前n项和的最值问题,笔者设计了如下题组.学生通过解题回顾,总结规律,轻松习得知识.
题组一:等差数列的公差为d,a1=-24,从第10项开始为正数,则公差d的取值范围为________.
题组二:等差数列的公差为d,a1=-24,从第10项开始为正数,试分析其前n项和Sn的单调性;有无最值?若有,是最大值还是最小值?
学生众:在上一题的基础上,学生很快抓住了问题的实质,轻松获解.
题组三:等差数列{an}中,an=24-2n,试问其前n项和Sn有最值吗?若有,是最大值还是最小值?当n为何值时取得?
学生众:在上两题的基础上,迅速得出a12=0,a11>0,a13<0,从而得出(Sn)min=S11=S12.
教师:请回顾以上解题过程,归纳等差数列前n项和Sn,何时有最值?是最大值还是最小值?
学生众:讨论片刻,达成共识.
学生甲:若等差数列的首项a1>0,公差d<0,则前n项和Sn有最大值;若等差数列的首项a1<0,公差d>0,则前n项和Sn有最小值.问题的关键是寻找等差数列的正数项和负数项的分界.
说明:等差数列的通项公式本质是一次函数,求和公式本质是必经过原点的二次函数(公差不为0时),这些经验积累有助于学生在解决相关问题时迅速调用其本质模型解决问题,增强了问题解决的能力.
三、通过数学思想透视本质
数学思想是认知数学问题本质的又一途径,也是课程标准中一直致力于学生思维培养的终极目标.培养学生问题解决能力,要让学生从问题中找到解决的最好思路,需要站在更高的视角来看待问题.课程制定组组长东北师大史宁中教授在一次讲解课程标准中指出:“数学解题学到最后是学思想方法,有思想方法就可以认识问题的本质,就可以比较轻松地解决问题.”中学数学有很多思想方法,但是比较重要的还是转化化归思想、数形结合思想等少数几个.笔者认为,想要更好地提高学生问题解决的能力,也可以从思想方法的视角去透视数学问题的本质.

(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
解析:(1)求函数f(x)的导数f′(x)=ax2-2bx+2-b,由函数f(x)在x=x1处取得极大值,在x=x2处取得极小值,知x1、x2是f′(x)=0的两个根,所以f′(x)=a(x-x1)(x-x2).当x<x1时,f(x)为增函数,f′(x)>0,由x-x1<0,x-x2<0,得a>0.
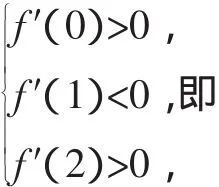
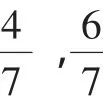
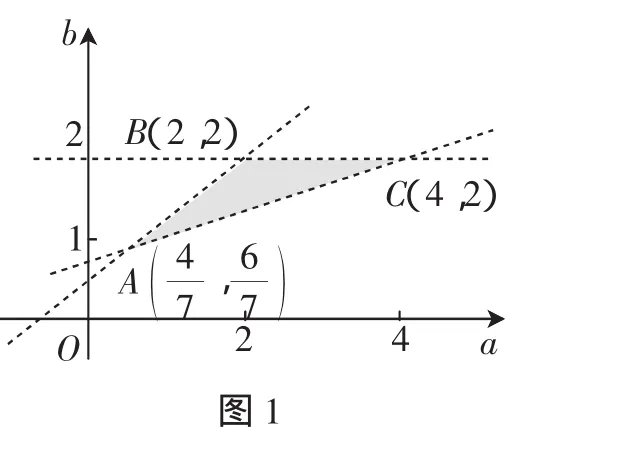
说明:本题第(2)问是从根的关系入手解决代数式z=a+2b,通过简单分析我们可以知道,其实质是线性规划问题,是利用图形的方式解决代数问题.这些问题只要学生在得到类似的三组导数关系式时就可以比较轻松地感受到数形结合思想的存在,其本质线性规划的使用,这样的问题尝试解决有助于问题解决能力的培养.
总之,数学问题本质有很多方面值得教师去挖掘和探索,只有将数学问题解决的本质给予呈现,才有利于学生对于数学知识的理解和运用,才能真正培养其问题解决的能力.本文从三个方面进行了一些论述,以笔者自身的经验和认知做出了一些浅显的描述,恳请读者以笔者之砖进行更细致的探索.
1.武瑞雪.对中学数学建模教学的探讨[J].教学月刊,2012(12).
2.朱永祥.再谈数学思想方法的挖掘和运用[J].中学数学(上),2013(2).F
