空间向量在立体几何存在性问题中的应用探究
2015-08-27江苏省海门中学徐巧石
☉江苏省海门中学 徐巧石
向量是近代数学中基本和重要的数学概念之一,它沟通了代数、几何和三角,是一种工具性的知识,有着极为丰富的实际背景.空间向量为处理立体几何问题提供了新的视角.空间向量的引入,为解决三维空间中的图形位置关系与度量问题提供了一个十分有效的工具.
对于空间向量的考查,通常是以立体几何为载体,“落脚点”在于应用.应用分两个方面:一是空间图形位置关系的判定,二是角度的度量.本文主要探讨空间向量在立体几何存在性问题中的应用.此类问题通常也称为探索性问题,具有一定的难度,需要学生熟练掌握空间图形的位置关系,通过反复尝试寻找到问题的答案.
一、回归课本,寻根探源
存在性问题在课本中共有五道习题涉及,这为此类问题回归课本找到了依据.
1.(苏教版选修2-1,第119页,13)如图1,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AF=1,M是线段EF的中点.
(1)略;
(2)略;
(3)试在线段AC上确定一点P,使PF与BC所成的角是60°.
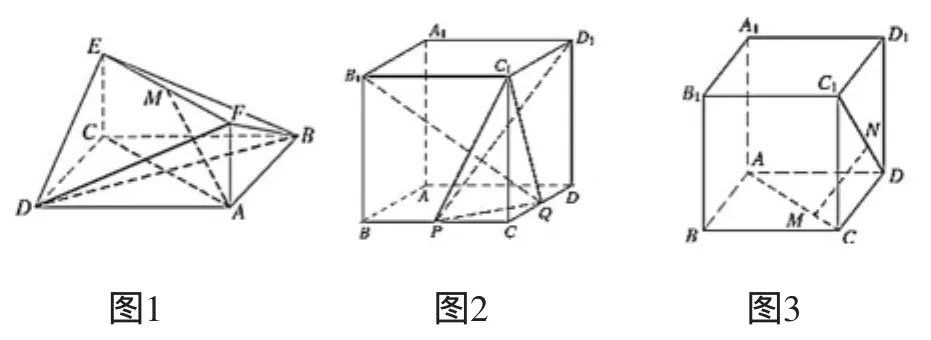
评注:(3)考查的是两直线夹角的计算,与直接求夹角不同,它是从相反的方向出发,已知两直线的夹角,求满足条件的动点.解这个问题有两个注意点:①设点P的坐标时需要注意动点P在线段AC上,其横、纵坐标相等并且满足0≤x=y≤;②两直线的夹角θ与两直线的方向向量的夹角α之间满足|cosα|=cosθ.
2.(苏教版选修2-1,第115页,15)在如图2所示的坐标系中,正方体ABCD-A1B1C1D1的棱长为2,P、Q分别是BC、CD上的动点,且PQ=
(1)确定点P、Q的位置,使得B1Q⊥D1P;
(2)略.
评注:(1)同样考查的是两直线夹角的计算,与1(3)的区别是:①两直线的夹角是特殊值直角;②动点增加为两个.两个注意点:①P、Q两点的坐标满足点P在线段BC上,点Q在线段CD上,并且PQ=;②对于两直线的夹角为直角,可直接利用=0找到等量关系.
3.(苏教版选修2-1,第119页,9)如图3,已知正方体ABCD-A1B1C1D1的棱长为1,MN是异面直线AC与C1D的公垂线段,试确定点M在AC上及点N在C1D上的位置.
评注:本题仍是对两直线夹角的计算的考查,与1、2两题不同之处在于它有两组直线MN和AC、MN和C1D分别垂直且含有两个动点M、N,从动点个数和直线夹角数两方面进行了延伸,解答时仍需要注意两动点M、N的坐标所满足的条件.
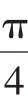
(1)略.
(2)在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定点E的位置;若不存在,试说明理由.
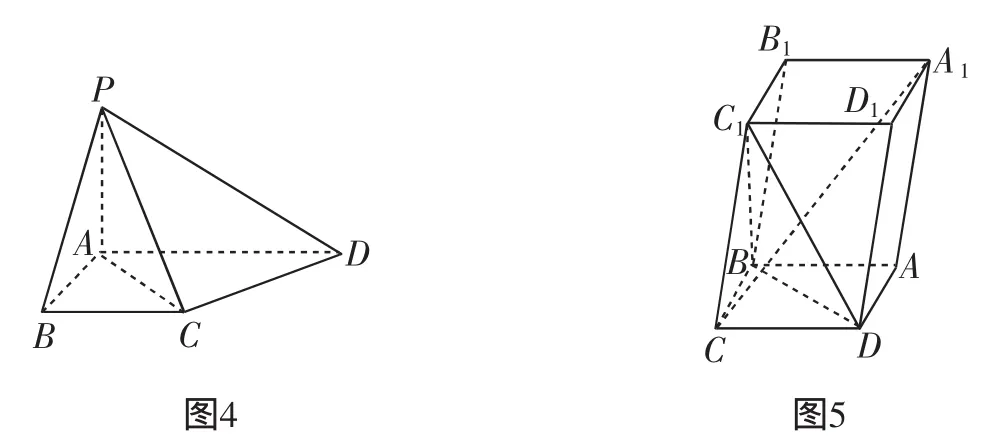
评注:(2)考查的是直线与平面的位置关系,已知直线与平面平行求相应点的坐标.若直线CE与平面PAB平行,只需满足CE的方向向量与平面PAB的法向量垂直,且直线CE不在平面PAB上即可.
5.(苏教版选修2-1,第118页,8)如图5,平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=θ.
(1)略;
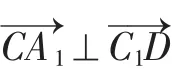
二、转换角度,识其本质
上述5题都是存在性问题,对于它们的求解,只需将题中所给的结论当做已知条件进行反推找到相应的等价条件即可,这也体现了数学思想中等价转化思想和解题时的逆向思维.
对于这5道题的考查载体,我们可以进一步进行划分.1、2、3题考查的是直线与直线的夹角.如果两直线的夹角是直角,则只需利用两直线的方向向量的数量积为0即可,如果不是直角,则要利用两直线的方向向量的夹角α与两直线的夹角θ之间满足的等式|cosα|=cosθ.4、5两题考查的是直线与平面的夹角中的两类特殊情况平行和垂直.如果平行,则利用直线的方向向量与平面的法向量垂直,如果垂直,则利用直线的方向向量与平面的法向量平行即可.
从角的角度来讲,线线角、线面角的存在性问题书中习题都已经有所涉及,面面角的存在性问题没涉及,因此很有可能以考查面面角为载体,出存在性的问题.
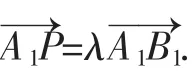
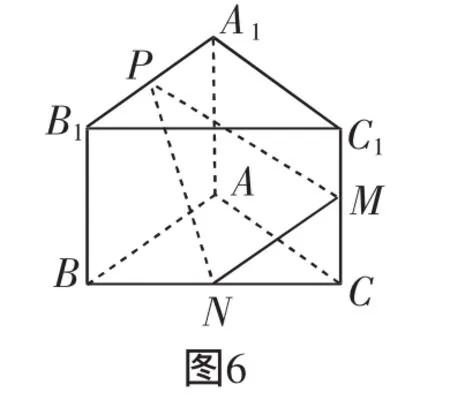
若平面PMN与平面ABC所成的二面角为45°,试确定点P的位置.
评注:解题的关键是利用二面角θ与两平面的法向量的夹角α之间满足|cosθ|=|cosα|,sinθ=sinα.
三、链接高考,推测可能

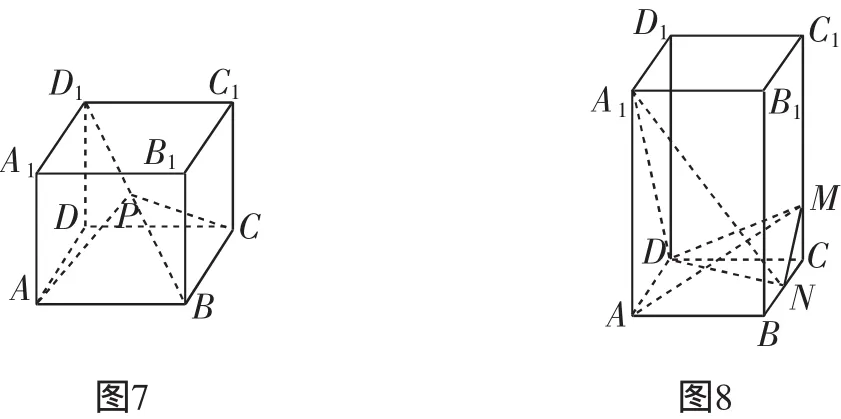
8.(2011年高考江苏附加题,22)如图8,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,点N是BC的中点,点M在CC1上.设二面角A1-DN-M的大小为θ.
(1)当θ=90°时,求AM的长;
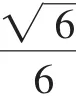
纵观这两题,共同点是都存在一个动点,所求问题都和这个动点有关.7中通过两直线的夹角把动点联系起来,8中通过二面角将动点联系起来.由已知条件先确定动点位置,再求解其他结果.以角为着眼点,动点还有可能通过线面角联系起来.
对于空间向量在立体几何存在性问题中的应用问题,只要紧紧抓住两角之间满足的关系这一主线,同时注意动点的坐标所满足的条件,建立等式,万变不离其宗,问题可迎刃而解.
