图的(2,1)-点面标号*1
2015-08-18陈东
陈 东
(浙江师范大学 行知学院,浙江 金华 321004)
图的(2,1)-点面标号*1
陈 东
(浙江师范大学 行知学院,浙江 金华 321004)
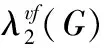
图;距离2标号;(2,1)-点面标号;外平面图
0 引 言
著名的距离 2 标号问题源于这样的一个无线电频道分配问题:给一个无线电网络中的发射站分配频道,为了避免干扰,要求相邻的发射站使用的无线电频道差值至少为2,同时要求距离为2的2个发射站使用不同的频道.该问题也被称为L(2,1)-标号问题.1992年,Griggs等[1]首先提出并研究了图的L(2,1)-标号问题.此后,这个概念被国内外同行广泛研究,详见文献[2-7].
把一个平面图看作是一个无线电网络,并为网络中的所有发射站分配无线电频率:在平面图上的每个顶点处设置一个发射站,要求图上相邻2个顶点所对应的发射站使用不同的频道;并在图上的每个面内设置一个发射站,要求图上相邻2个面所对应的发射站使用不同的频道;此外,为了避免干扰,要求图上每个顶点及其所在面所对应的发射站使用的频道差值至少为2.
为解决上述问题,可以构建如下数学模型:设G是一个可平面图,G(V,E,F)是G在平面上的一个嵌入,其中V,E,F分别代表G的顶点集合、边集合及面集合.

设c是图G的一个k-(2,1)-点面标号.对于任意的元素x∈V∪F,定义c′(x)=k-c(x).显然,c′也是图G的一个k-(2,1)-点面标号,于是称c和c′为对称标号.
根据定义1,很容易得到一个平面图G的(2,1)-点面标号数的平凡上下界
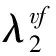

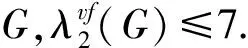
本文首先研究了一些简单图类的(2,1)-点面标号问题,给出了树、圈、欧拉二部图、K4、外平面图等图类的(2,1)-点面标号数的上界.此外,重点讨论了外平面图的(2,1)-点面标号问题,完全刻画了至多含有一个闭内面的外平面图的(2,1)-点面标号数.
1 一些简单图类的(2,1)-点面标号
若无特殊说明,本文只考虑简单的平面图,并且直接使用G表示它在平面上的嵌入.对于一个面及其边界路上的点和边,称这三者是两两关联的.一个面的度定义为该面上边界路中出现的边的数量.若f的度是奇数,则称f为奇面,否则称为偶面.下面将给出几个简单图类的(2,1)-点面标号数的上界.
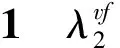

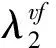
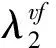
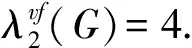
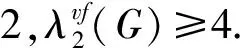
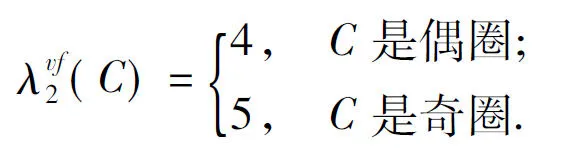
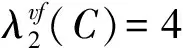
设c是图G的一个(2,1)-点面标号,uv是G中的一条边.若{c(u),c(v)}={a,b},为方便叙述,则可将uv称为一条(a,b)e-边.
引理1设c是2-连通图G的一个5-(2,1)-点面标号,那么G中只可能有(0,1)e-边,(0,2)e-边,(0,5)e-边,(1,2)e-边,(2,3)e-边,(3,4)e-边,(3,5)e-边及(4,5)e-边.
证明 因为G是2-连通图,所以每条边至少关联2个面.注意到,c所使用的标号集合为{0,1,2,3,4,5}.如果G中有(0,3)e-边,那么该边关联的2个面无法正常标号,这是一个矛盾.对于其他的边,同理可以推出矛盾.引理1证毕.
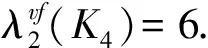
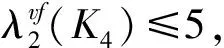
接下来直接给出K4的一个6-(2,1)-点面标号,如图1所示.
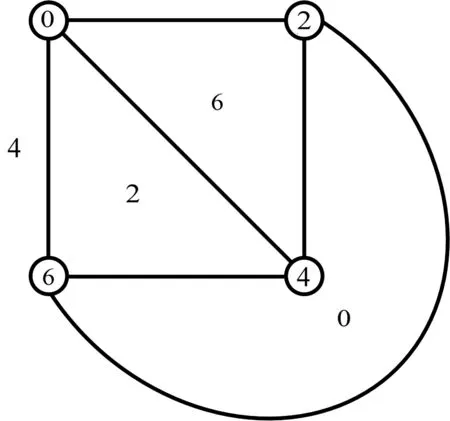
图1 K4的一个6-(2,1)-点面标号
为方面叙述,定义
Fabc={f∈F(K4)|f关联的3个点的标号分别为a,b,c}.

2 外平面图的(2,1)-点面标号
设G是一个外平面图,令f0是G的外面.若G的某一个内面全是由内边组成,则称其为闭内面,反之为开内面.若一个外平面图不存在闭内面,则称其为开外平面图.另外,定义G的内面对偶图G*如下:把G的每一个内面看作是G*的一个点,G*中2个点有边连接当且仅当它们在G中对应的内面有公共边,同时删除重边使得G*是一个简单图.
引理2设G是一个连通的外平面图,如果G*是G的内面对偶图,那么G*是一个森林.

设f1,f2是外平面图G的2个内面,把f1与f2在G*中对应点间的距离定义为G中这2个内面f1与f2之间的距离,记为d(f1,f2).由引理2可知,G的任意2个内面之间的距离是唯一的.

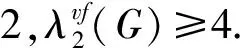
因为G是外平面图,所以G的点色数是3,因此,可以对G中的点使用标号0,1,2.根据引理2,G的内面对偶图是树,那么可以为G的所有内面指定标号4和5.最后,令G的外面的标号为6.这样,就得到了G的一个6-(2,1)-点面标号.定理6证毕.
根据定理6,一个2-连通外平面图的(2,1)-点面标号数只有3种可能:4,5或6.再根据定理3,当2-连通外平面图不是欧拉二部图时,其(2,1)-点面标号数不是5就是6.那么,寻找2-连通外平面图(2,1)-点面标号数的刻画条件就变得非常有意义.
引理3设G是一个2-连通外平面图,并且G含有一个奇内面f1.如果G有一个5-(2,1)-点面标号c,那么f1上一定有标号为2或3的点;如果G还是一个2-连通开外平面图,那么G的点标号集合一定是{0,1,2}或{3,4,5},对应的面标号集合一定是{3,4,5}或{0,1,2}.
证明 利用反证法,首先假设f1上没有标号为2或3的点.注意到,c所使用的标号集合为{0,1,2,3,4,5}.根据标号的对称性,对于f1上任意的一条边e,e只可能为(0,1)e-边,(0,4)e-边,(0,5)e-边和(1,4)e-边,但是这些可能性都与引理1矛盾.根据e的任意性,奇面f1中的点标号都是0或1.事实上,奇面上的点至少需要3个标号,这是一个矛盾.因此,f1上一定有标号为 2 或 3 的点.
下面考虑当G是一个2-连通开外平面图时的情况.假设G中点的标号集合既不是{0,1,2},也不是{3,4,5}.根据之前的讨论及标号的对称性,不妨设f1中的点u的标号为2.显然,f1上不存在标号为4或者5的点,否则f1和外面f0必须使用同一个标号0,这是一个矛盾.于是,假设f1上存在点v使得c(v)=3,那么{c(f1),c(f2)}={0,5}.进而推知,f1上的点的标号只能是2或者3,这与奇圈f1上的点至少需要3个标号矛盾.因此,f1上的点标号集合是{0,1,2},并且标号集合中的每个标号都会被用到.容易推断,G中其他点的标号也只能来自于{0,1,2},否则会造成外面f0无标号可用.引理3证毕.
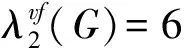
1)假设G存在一个无2-点的奇内面f1.根据引理3及标号的对称性,不妨设f1上有个点u使得c(u)=2.又因为f1上没有2-点,所以d(u)≥3.于是,假设uv是f1关联的一条内边,f2是uv关联的另一个内面.因为c(u)=2,所以c(f0),c(f1),c(f2)∈{0,4,5}.又因为G是一个开外平面图,所以f0,f1,f2两两相邻,也就是说,它们的标号必须两两不同.因此,{c(f0),c(f1),c(f2)}={0,4,5}.但是,标号为0和4的这2个面是相邻的,这会导致这2个面公共边上的2个顶点无标号可用,矛盾.
2)假设G存在2个距离为奇数的奇内面f1和f2.根据引理3及标号的对称性,不妨设G的每一个奇内面上有点标2,并且G的点标号集为{0,1,2},那么奇面与外面f0的标号集合就是{4,5},偶面的标号集合就是{3,4,5}.设c(f0)=a∈{4,5},则G中所有奇面的标号都是b={4,5}{a}.因为G是开外平面图,每个内面都与外面相邻,所以内面可用的标号集就是{3,b}.根据引理2,G的内面标号一定是3和b交替分布.也就是说,奇面f1和f2之间的距离应该是偶数,这与假设矛盾.
1)任意选择G的一个终端面,并为这个终端面及其关联的点分配标号.
易知,这样的终端面是存在的,并且这个终端面一定是由一条内边e=uv及一条除端点u,v外都是2-点的路P围成.首先,令u和v的标号分别为0和1.然后,除u,v外,如果P中还有偶数个点,那么对它们依次使用标号0和1;如果还有奇数个点,那么可以使用0,1和2为这些点标号.容易验证,这种标号分配方式是合理的,并且唯一的内边e的2个端点的标号为0和1.
2)任意选取一个只有一条获得标号的内边且其标号是0和1的内面,并对这个面及其关联的点标号.
如果这个内面是偶面,那么按照已有的标号顺序,为剩下的点依次分配标号0和1;如果这个内面是奇面,那么按照已有的标号顺序,为剩下的同时属于内边的点(一定恰好就是该面中度数至少为3的点)依次分配标号0和1.因为每个奇内面都有2-点,所以可以为剩下的2-点依次分配标号0,1和2.容易验证,这种标号分配方式也是合理的,并且每条内边的2个端点的标号为0和1.
3)重复2),直到G的每个点都有标号.
至此,每条内边所对应的点的标号都是0和1,奇内面至少有一个2-点标号为2,偶内面所有点的标号都是0和1.
4)令外面的标号为5,奇内面的标号为4,其他内面的标号用3和4交替分配.
因为任意2个奇内面的距离都是偶数,所以由引理2可以确定这种标号分配方式是合理的.

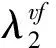
注1根据定理7必要性的证明可以发现如下事实:一个好的2-连通开外平面图G,一定存在着一个5-(2,1)-点面标号使得下列命题成立:1)G中的点的标号集为{0,1,2},只有2-点的标号可能为2,度数至少为3的点的标号一定是0或者1;2)G中内面的标号集为{3,4},奇内面的标号一定为4;3)G的外面标号为5.
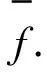

例1如图2(a)所示,G是一个2-连通外平面图,v1,v4,v10构成的G的唯一闭内面.图2(b)中3个部分按顺时针顺序分别是G的v1v4-极大开子图Gv1v4,v4v10-极大开子图Gv4v10及v10v1-极大开子图Gv10v1.
图2 G和G的极大开子图

证明 由于G的每个极大开子图都是一个2-连通的开外平面图,所以根据定理6和定理7,充分性显然成立.对于命题的必要性,使用反证法,只要证明:当G的每一个极大开子图都是好的,G却存在一个5-(2,1)-点面标号.
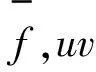

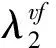

1)每个极大开子图点的标号集为{0,1,2},只有2-点的标号可能为2,度数至少为3的点的标号一定是0或者1;
2)每个极大开子图中内面的标号集为{3,4},奇内面的标号一定为4;
3)每个极大开子图的外面标号为5.

必要性 使用反证法,只需证明G在下述3种不同情况下都不存在5-(2,1)-点面标号即可:
1)G有一个极大开子图Guv是坏的.
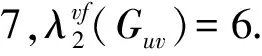



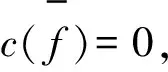
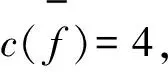
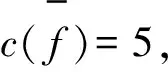


另一方面,因为Guv是一个2-连通的开外平面图,并且Guv中有奇内面f1,由引理3及c(f2)∈{4,5}可知,f1上一定有标号为 2的点.那么,c(f1),c(f0)∈{4,5}并且c(f1)≠c(f0).
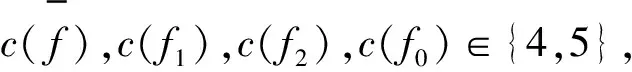
[1]Griggs J R,Yeh R K.Labelling graphs with a condition at distance two[J].SIAM J Discrete Math,1992,5(4):586-595.
[2]Chang G J,Guo D.TheL(2,1)-labelling problem on graphs[J].SIAM J Discrete Math,1996,9(2):309-316.
[3]Borodin O V.A new proof of the 6 color theorem[J].J Graph Theory,1995,19(4):507-521.
[4]Sakai D.Labelling chordal graphs: distance two condition[J].SIAM J Discrete Math,1994,7(1):133-140.
[5]Wang Weifan,Liu Jiazhuang.On the vertex face total chromatic number of planar graphs[J].J Graph Theory,1996,22(1):29-37.
[6]Wang Weifan,Lih K W.Labelling planar graphs with conditions on girth and distance two[J].SIAM J Discrete Math,2004,17(2):264-275.
[7]Zhu Haiyang,Hou Lifeng,Chen Wei,et al.TheL(p,q)-labelling of planar graphs without 4-cycles[J].Discrete Appl Math,2014,162(1):355-363.
(责任编辑 陶立方)
The(2,1)-totallabellingoftheproductoftwokindsofgraphs
CHEN Dong
(XingzhiCollege,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)
Ak-(2,1)-coupled labelling of a plane graphGwas defined as a mapping fromV(G)∪F(G) to {0,1,…,k} such that adjacent vertices or adjacent faces
different numbers, and numbers of the vertex and the face incidentally received differed by at least 2. The (2,1)-coupled labelling numberλvf2(G) ofGwas defined as the smallest integerksuch thatGhad ak-(2,1)-coupled labelling. A tight upper bounds of (2,1)-total labelling number were given for trees, cycles,K4, Eulerian bipartite graphs, outerplanar graphs, etc. In addition, a complete characterization of (2,1)-coupled labelling numbers for outerplanar graphs with at most one closed inner face was presented.
graph; distance two labelling; (2,1)-coupled labelling; outerplanar graph
10.16218/j.issn.1001-5051.2015.02.005
2015-03-21
国家自然科学基金资助项目(11401535)
陈 东(1981-),男,浙江金华人,讲师.研究方向:图论与组合数学.>
O157.5
A
1001-5051(2015)02-0148-08
