具有自旋轨道耦合的冷原子费米气中的拓扑超流和FFLO超流*1

王 俊， 高先龙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

具有自旋轨道耦合的冷原子费米气中的拓扑超流和FFLO超流*1

王 俊， 高先龙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

研究了具有自旋轨道耦合的冷原子费米气在外磁场作用下的物理性质.通过自洽求解Bogoliubove-de Gennes方程，发现了在不同磁场强度和粒子填充数下，体系分别存在拓扑超流态和Fulde-Ferrell-Larkin-Ovchinnikov超流态.当体系处于拓扑超流态时，存在零能Majorana费米子.

自旋轨道耦合；拓扑超流；Majorana费米子；FFLO超流

0 引 言

最近几年，冷原子物理实验取得了突破性的进展，实验人员先后实现了多种凝聚态强关联体系的模拟，如费米超流、Hubbard模型[1]等.但是由于原子是中性粒子，所以利用冷原子模拟带电粒子在电磁场中的运动一直是件困难的事.不过自2009年以来，美国国家标准局的Spielman小组根据双光子拉曼耦合方案，先后实现了人造规范场、自旋轨道耦合的玻色-爱因斯坦凝聚体[2].随后,山西大学王鹏军等[3]实现了费米子的自旋轨道耦合.这些技术的突破不仅为模拟研究许多量子现象提供新的实验平台，也为理论研究带来了更大的机遇与挑战.

研究发现，当s波配对的简并费米气加上自旋轨道耦合和外磁场后，可以形成一种新的量子态：拓扑超流态[4-5]，它具有零能的准粒子激发态，正是所谓的Majorana费米子[6].Majorana 费米子遵循非阿贝尔[7]交换统计，并且不受局域微扰影响而导致退相干，可以用来进行拓扑量子计算[8]，因此，在更多的材料中找到Majorana费米子已成为最近研究的热点[9].

另外，当简并费米气体不存在自旋轨道耦合、只加入足够大的外磁场时，研究表明，此时体系也会发生奇异的、质心动量不为零的Cooper配对，即所谓的Fulde-Ferrell-Larkin-Ovchinnikov(FFLO)配对[10-11].FFLO 超流不同于拓扑超流，并不产生零能的Majorana费米子.因此，在具有自旋轨道耦合的费米气中，能否发现FFLO 超流态，也引起了关注[12-13].

本文主要研究了一维光晶格中具有自旋轨道耦合的量子简并费米气体，探究其在不同外磁场强度和不同粒子填充数时的状态性质.因为在冷原子物理实验中，已经能够实现人造磁场、自旋轨道耦合等技术，并且参数完全可控.所以,该理论模型研究可以应用到冷原子实验中，为实验研究提供理论依据.

1 理论模型

考虑光晶格中具有自旋轨道耦合和外磁场的一维简并费米气体.该体系的哈密顿量可描述为

H=H0+HZ+HSO. (1)

式(1)中，第1项就是标准的费米哈伯德模型：

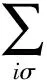
式(2)中：t表示跃迁振幅；μ是化学势；U为吸引相互作用.

另外,式(1)中第2项是Zeeman场项:

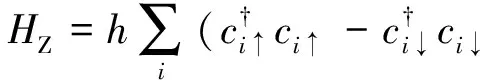
式(1)的第3项是自旋轨道耦合项：

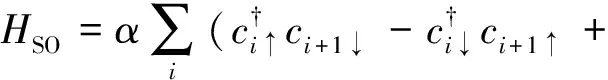
对上述哈密顿量进行平均场处理，可以得到一个有效哈密顿量

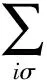
式(5)中，Δi=-U〈ci↓ci↑〉为超流配对序参量，它描述了格点i处由吸引相互作用诱发的s波配对的强度.由于在一维s波配对体系中引入自旋轨道耦合，所以通过自旋轨道耦合效应并利用外磁场破坏时间反演对称性，可得到类似于p波配对的超流体，而Kitaev已经论证了一维p波配对体系的两端会出现Majorana费米子[14].

这里

h0=-t(δi+1j+δi-1j)-μiδij+hδijσz+iσyα(δi+1j-δi-1j).

(8)

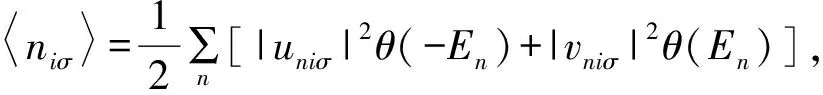
(9)

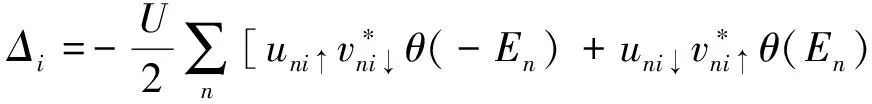
式(10)中，函数θ(En)表示零温时的费米-狄拉克分布.通过粒子平均占据数方程(9)和超流序参量方程(10)，BdG方程(6)可以自洽地求解.在下面的分析中，令跃迁振幅t为单位能量，吸引相互作用强度U=4.5，自旋轨道耦合强度α=1.0，并选用开边界条件.

2 结果分析与讨论

2.1拓扑超流与Majorana费米子

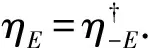
笔者用数值求解了体系在平均粒子填充数n=0.3时的情况,发现当磁场强度h≥1.0时，能谱的能隙关闭，即出现零能解，且此时超流序参量并不为零.上述特征表明，体系进入到拓扑超流态.另外,也可以通过探测Majorana费米子是否存在来作为体系是否进入拓扑超流态的依据.在实验上，可以运用空间分辨的射频谱(radio-frequency spectroscopy)技术[17]测量局域态密度来探讨Majorana费米子.其中,局域态密度定义为

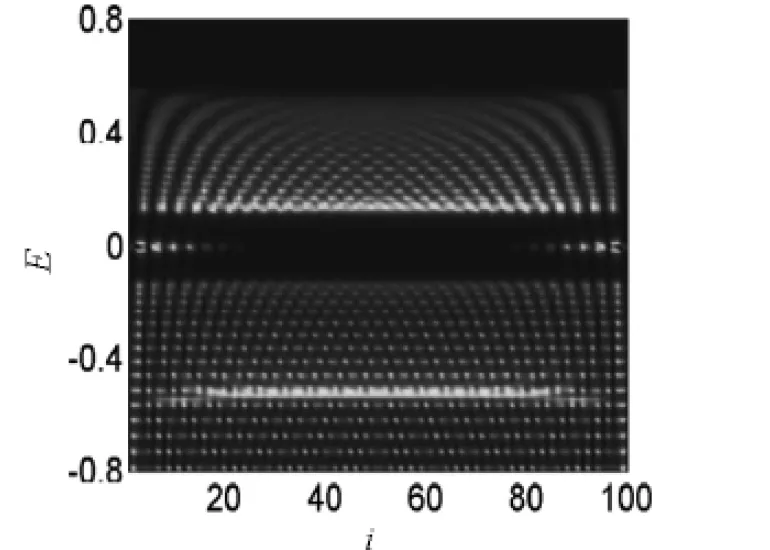
图1 h=1.1时，自旋向上粒子的局域态密度ρ↑(i,E)

图2 h=1.1时，自旋向下粒子的局域态密度ρ↓(i,E)

图3 h=1.4时，配对序参量Δi随格点的变化

图1和图2分别为外磁场强度h=1.1时，自旋向上粒子的局域态密度ρ↑(i,E)和自旋向下粒子的局域态密度ρ↓(i,E).从图1和图2可以看到，在零能附近，局域态密度于体系的两端各有一个极大值，这正是来自于一对Majorana费米子波函数的贡献.另外，笔者还发现，区别于其他准粒子，Majorana费米子局域在体系的两端彼此空间分离.

2.2FFLO超流现象

在不考虑自旋轨道耦合时,自旋向上的粒子和自旋向下的粒子由于外磁场对电子磁矩的作用使得2种费米子的费米面错开.两费米面的自旋完全极化，配对只能发生在2个费米面之间.若此时2组分不均匀(N↑≠N↓)，则可发生FFLO配对，其特点是配对序参量Δi随格点振荡.但是，当体系存在自旋轨道耦合时，自旋轨道耦合会使自旋发生翻转.这时处于同一费米面的2个粒子也有可能发生配对，形成BCS超流[18].所以,当体系存在自旋轨道耦合时，FFLO超流现象是否还能存在引起了我们的关注.

通过研究发现，在平均粒子填充数n=1.0附近，当外磁场的强度达到一定值时，体系仍然可以发生FFLO超流现象.当外磁场强度h=1.4时，体系的配对序参量如图3所示.从图3中明显可以看到，序参量Δi随格点振荡，这正是体系处于FFLO超流态的特征.

3 总 结

本文研究了一维光晶格中具有自旋轨道耦合的冷原子费米气体系的物理性质，发现存在自旋轨道耦合时，当外磁场的强度增大到一定值时，能谱会出现零能简并，体系会进入拓扑超流态,并且此时会有一对Majorana费米子分别局域在体系的两端.另外,笔者还发现，具有自旋轨道耦合时，在粒子填充数n=1.0附近体系仍然可以发生FFLO超流现象.

下一步，笔者将进一步研究不同自旋轨道耦合强度、吸引相互作用强度等对体系状态的影响，解决各个参数平面下的相图问题.另外，若在体系中引入无序，考虑无序对该体系状态的影响，也是一个有意义的问题.

[1]Lewenstein M,Sanpera A,Ahufinger V,et al.Ultracold atomic gases in optical lattices:mimicking condensed matter physics and beyond[J].Advances in Physics,2007,56(2):243-379.

[2]Lin Yuju,Jimenez-Garcia K,Spielman I B.Spin-orbit-coupled Bose-Einstein condensates[J].Nature,2011,471(7336):83-86.

[3]Wang Pengjun,Yu Zengqiang,Fu Zhengkun,et al.Spin-orbit coupled degenerate Fermi gases[J].Physical Review Letters,2012,109(9):095301.

[4]Zhang Chuanwei,Tewari S,Lutchyn R M,et al.Px+ipysuperfluid froms-wave interactions of fermionic cold atoms[J].Physical Review Letters,2008,101(16):160401.

[5]Liu Xiaji,Jiang Lei,Pu Han,et al.Probing majorana fermions in spin-orbit-coupled atomic Fermi gases[J].Physical Review A,2012,85(2):021603.

[6]Wilczek F.Majorana returns[J].Nature Physics,2009,5(9):614-618.

[7]王一飞,龚昌德.拓扑平带上的分数量子反常霍尔效应 (一)[J].浙江师范大学学报:自然科学版,2013,36(4):361-371.

[8]Nayak C,Simon S H,Stern A,et al.Non-Abelian anyons and topological quantum computation[J].Reviews of Modern Physics,2008,80(3):1083.

[9]高先龙,陈捷,陈阿海.一维费米原子系统中的拓扑超流和Majorana费米子[J].浙江师范大学学报:自然科学版,2013,36(4):372-378.

[10]Wu Fan,Guo Guangcan,Zhang Wei,et al.Unconventional superfluid in a two-dimensional Fermi gas with anisotropic spin-orbit coupling and Zeeman fields[J].Physical Review Letters,2013,110(11):110401.

[11]Liao Y A,Rittner A S C,Paprotta T,et al.Spin-imbalance in a one-dimensional Fermi gas[J].Nature,2010,467(7315):567-569.

[12]Liu Xiaji,Hu Hui.Topological superfluid in one-dimensional spin-orbit-coupled atomic Fermi gases[J].Physical Review A,2012,85(3):033622.

[13]Qu Chunlei,Gong Ming,Zhang Chuanwei.Fulde-Ferrell-Larkin-Ovchinnikov or Majorana superfluids:The fate of fermionic cold atoms in spin-orbit-coupled optical lattices[J].Physical Review A,2014,89(5):053618.

[14]Kitaev A Y.Unpaired Majorana fermions in quantum wires[J].Physics-Uspekhi,2001,44(S10):131.

[15]De Gennes P G.Superconductivity of metals and alloys(advanced book classics)[M].Boston:Addison-Wesley Publ,1999.

[16]Lutchyn R M,Sau J D,Sarma S D.Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures[J].Physical Review Letters,2010,105(7):077001.

[17]Shin Y,Schunck C H,Schirotzek A,et al.Tomographic rfspectroscopy of a trapped Fermi gas at unitarity[J].Physical Review Letters,2007,99(9):090403.

[18]Liang Junjun,Zhou Xiaofan,Chui P H,et al.Spin-orbit coupling induced unconventional pairings in a one-dimensional lattice[J].arXiv preprint arXiv:1404.3009,2014.

(责任编辑 杜利民)

TopologicalsuperfluidsandFFLOsuperfluidsinspin-orbitcoupledatomicFermigases

WANG Jun, GAO Xianlong

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was investigated the properties of spin-orbit coupled atomic fermi gases under a Zeeman field. By solving the Bogoliubove-de Gennes equation self-consistently, it was found that the system supported the topological superfluid state and the Fulde-Ferrell-Larkin-Ovchinnikov superfluid state respectively when the system under the different strength of Zeeman field and filling factors. When the system turned into topological superfluid state, a pair of zero-energy Majorana fermions were found.

spin-orbit coupling; topological superfluids; Majorana fermion; FFLO superfluids

10.16218/j.issn.1001-5051.2015.02.002

2015-01-10

国家自然科学基金资助项目(11374266;11174253)

王 俊(1989-),男，浙江台州人，硕士研究生.研究方向：凝聚态物理.

高先龙.E-mail: gaoxl@zjnu.cn

O562.4

A

1001-5051(2015)02-0129-04