三条路的笛卡尔乘积图的L（1，2）-标号数

饶威丽，吴 琼，李 莹

（天津职业技术师范大学理学院，天津 300222）

当今世界，随着计算机无线网络的迅猛发展，网络代码资源日渐紧缺，因此对有限的无线网络代码资源进行合理优化分配显得尤为重要。在计算机无线网络中，如果2 个站点距离“非常近”，则存在直接干扰，为了避免直接干扰，要求站点的代码不同，假设差异为j；而如果2 个站点距离“比较近”且与同一个站点距离“非常近”，则存在间接干扰，而这样距离较近的站点之间为了避免直接干扰，同时也要避免间接干扰，就要求这2 个站点的代码差异更大，假设差异为k，则有j≤k。基于这些条件，代码分配问题可抽象为图的L（j，k）-标号问题，它不同于无线电的频率分配问题概括出来的 L（j，k）-标号问题，这里 j≤k。在20 世纪 90 年代，Bertossi 等[1]阐述了一种模型，只要求距离较近的站点发射不同的代码，而忽略站点间的直接干扰，可概括为L（0，1）-标号问题。但在实际问题中，无论直接干扰还是间接干扰，都需要进行规避，所以在2005 年，Jin 等[2]提出了基于代码分配问题的L（j，k）-标号问题。到目前为止，基于代码分配问题的图的L（j，k）-标号问题的研究成果并不多，相关结论主要有：2007 年，牛庆杰[3]确定了路、圈和轮的 L（j，k）-标号数；在文献[4]中，作者确定了树和完全图的2 类乘积图的 L（j，k）-圆标号数；2013 年，Shiu 等[5]得到了路和圈 Direct 乘积图的 L（j，k）-标号数；Wu 等[6]确定了路和圈 Direct 乘积图的 L（j，k）-圆标号数并在文献[7]中给出了路和圈笛卡尔乘积图的L（j，k）-标号数；另外，Wu 等[8-9]分别给出了路的平方的 L（j，k）-圆标号数以及 L（j，k）-标号数；2018 年，文献[10-11]给出了广义彼得森图以及 Cactus 图的 L（j，k）-标号数，这里的j≤k。随着无线网络的不断发展，人们居住环境的日益密集，解决二维平面图的代码分配问题已不能缓解目前代码匮乏的问题。而作为刻画三维无线网络的最重要的图——三条路的笛卡尔乘积图，关于它的研究就显得尤为重要了。本文确定了任意长度的三条路的笛卡尔乘积图的L（1，2）-标号数，给出了相应图的最优标号方案，可直接被利用到三维无线网络的代码分配问题中，从而达到节约资源，提高经济效益的目的。

1 基本定义

定义1[11]标号问题的定义如下

设f 为一个从图G 的顶点集到非负整数集的映射，若符合条件

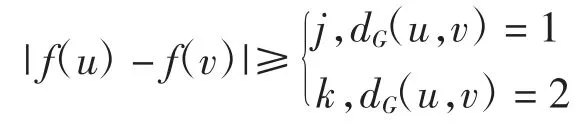
f 便为图 G 的一个 L（1，2）-标号。图 G 的 L（1，2）-标号数用λ1，2（G）表示，标号的最大值与最小值之间的差称为标号的跨度，而所有标号中最小的跨度则称为图 G 的 L（1，2）-标号数。

定义2设A、B、C 为集合，用A 中元素为第一元素，B 中元素为第二元素，C 中元素为第三元素构成有序组，所有这样的有序组组成的集合叫做集合A、B、C的笛卡尔积，记作A×B×C，即

A×B×C={（u，v，w）|u∈A∧v∈B∧w∈C}

定义3图G、图H 和图K 的笛卡尔乘积图是一个空间图，记为G▯H▯K，其顶点集合为V（G）×V（H）×V（K），顶点（u，v，w）和顶点（u′，v′，w′）相邻当且仅当（1）u=u′，v=v′且 ww′∈E（K）或者（2）u=u′，w=w′且 vv′∈E（H）或者（3）v=v′，w=w′且 uu′∈E（G）。

定义4[12]设G（V，E）是无向图，图G 中的一个顶点和边交替出现的非空序列P=v0e1v1e2…ekvk称为图G 的一条由顶点 v0到顶点 vk的路。其中 v0，v1，…，vk是图 G 的顶点，e1，e2，…，ek是图 G 的边。

定义 5图 Pl▯Pm▯Pn的顶点记为 va，b，c，其中 0≤a≤l-1，0≤b≤m-1，0≤c≤n-1 。为了方便叙述，把顶点 v0，0，0放在三维直角坐标系的原点，而顶点 va，b，c对应于空间直角坐标系中点（a，b，c）。

定义6设区间[M，N]，区间长度定义为N - M，记作|[M，N]|=N-M。

本文中涉及的其他相关概念请参阅文献[13]。

2 笛卡尔乘积图的 L（1，2）-标号数

引理1[4]令图H 是图G 的一个导出子图，则λ1，2（G）≥λ1，2（H）。

引理2[7]令 A、B、n 为正实数，有|[A]n- [B]n| =

引理 3令 A、B、n 为正实数，且 0≤A ＜ n，有[A+

证明

（1）若 0≤A+B ＜ n，0≤B ＜ n，即[A+B]n-[B]n=A+B-B=A。

（2）若 n≤A+B ＜ 2n，0≤B ＜ n，即[A+B]n-[B]n=A+B-n-B=A-n。

（3）若 B≥n，B=r+kn，kn≤B≤（k+1）n，kn≤A+B≤（k+2）n。

2.1 图P2▯Pm▯Pn的 L（1，2）-标号数

本节先讨论特殊情形 P2▯Pm▯Pn的 L（1，2）-标号数。

定理1λ1，2（P2▯P2▯P2）=6。

证明一方面，给图 P2▯P2▯P2一个标号 f 如下

f（v0，0，0）= f（v1，1，1）= 0；f（v0，1，0）= f（v1，0，1）= 2；

f（v1，0，0）=f（v0，1，1）=4；f（v1，1，0）=f（v0，0，1）=6。

不难验证，f 是图 P2▯P2▯P2的一个 L（1，2）-标号且跨度为6，即λ1，2（P2▯P2▯P2）≤6。

另一方面，因 v0，0，0、v1，0，1、v0，1，1、v1，1，0是互相距离为2 的4 个顶点，根据L（1，2）-标号的定义知λ1，2（P2▯P2▯P2）≥6 。

综上可得，λ1，2（P2▯P2▯P2）=6。

引理4设图H1如图1 所示，λ1，2（H1）=7。

图1 图H1

证明一方面，定义f 是图H1的一个标号，标号f如下

f（v0）=0；f（v1）=2；f（v2）=4；f（v3）=6；

f（u0）= 1；f（u1）=3；f（u2）=5；f（u3）=7。

不难验证，f 满足 L（1，2）-标号条件且跨度为 7，即λ1，2（H1）≤7。

另一方面，假设λ1，2（H1）＜7，令f 是图H1的一个L（1，2）-标号且其中标号子区间In=[n，n +1），n=0，1，…，6 。因为顶点 v0、v1、v2、v3相互之间距离为2，则它们的标号相互之间至少差2，即它们的标号应落在 I0∪I2∪I4∪I6中。又因为顶点 u1与 v0、v1、v2、v3这 4 个顶点都相邻，且标号子区间 I0、I2、I4、I6的长度均小于1，故f（u1）∈I1∪I3∪I5。又因顶点u0、u1、u2、u3相互之间距离为2。若f（u1）∈Ii，则

f（u0），f（u2），f（u3）∈[0，i - 1）∪[i + 2，7），其中i =1，3，5。

（1）若f（u1）∈I1∪I5，则f（u0），f（u2），f（u3）∈[3，7），或f（u0），f（u2），f（u3）∈[0，4）。因为f（u0），f（u2），f（u3）中任意2 个标号至少差2，所以它们最大标号和最小标号之间的差至少为 4，而区间[3，7）或[0，4）的长度小于 4，所以矛盾。

（2） 若 f（u1）∈I3，则 f（u0），f（u2），f（u3）∈[0，2）∪[5，7）。因为f（u0）、f（u2）、f（u3）中任意2 个标号至少差2，而区间[0，2）∪[5，7）的长度都小于 2，所以它们一共至多包含f（u0）、f（u2）、f（u3）中2 个标号，所以矛盾。故λ1，2（H1）≥7。

综上所述，λ1，2（H1）=7。

定理2若n∈N 且n≥3，则λ1，2（P2▯P2▯Pn）=7。

证明一方面，给图P2▯P2▯Pn定义一个标号 f 为

f（v0，y，0）=[5[y]4]8；f（v0，y，1）=[3（[y]4+1）]8；

f（v1，y，0）=[3（[y+2]4+1）]8；f（v1，y，1）=[5[y+2]4]8。

这里的 0≤y≤n-1，如图 P2▯P2▯P8的一个 7-L（1，2）-标号如图 2 所示。不难验证 f 满足 L（1，2）-标号的条件，且跨度为7，即当n≥3 时，λ1，2（P2▯P2▯Pn）≤7。

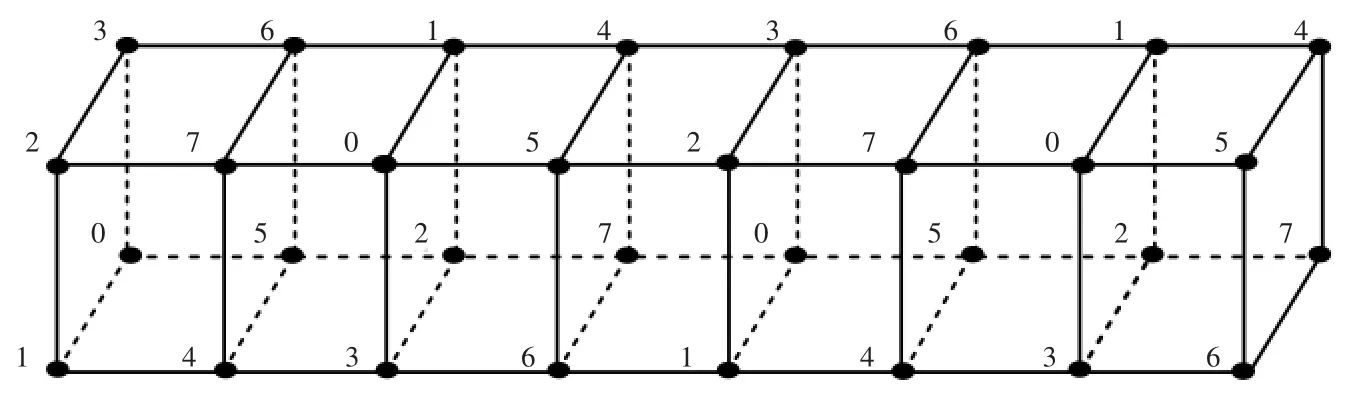
图 2 图 P2▯P2▯P8 的一个 7-L（1，2）-标号

另一方面，由引理4 可知λ1，2（H1）=7，又因图H1是图 P2▯P2▯Pn的一个导出子图，由引理 1 可知，λ1，2（P2▯P2▯Pn）≥λ1，2（H1）=7，这里的n≥3。

综上可得，当n≥3 时，λ1，2（P2▯P2▯Pn）=7。

引理5设图H2如图3 所示，λ1，2（H2）=9。

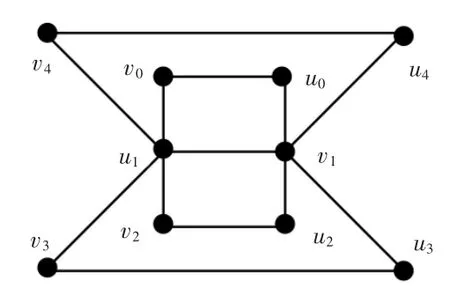
图3 图H2

证明一方面，定义f 是图H2的一个标号，标号f如下

f（v0）=0；f（v1）=2；f（v2）=4；f（v3）=6；f（v4）=8；

f（u0）=1；f（u1）=3；f（u2）=5；f（u3）=7；f（u4）=9。

不难验证，f 满足 L（1，2）-标号条件且跨度为 9，即λ1，2（H2）≤9。

另一方面，假设λ1，2（H2）＜9，令f 是图H2的一个L（1，2）-标号且其中标号子区间In=[n，n+1），n=0，1，…，8。因为顶点 v0、v1、v2、v3、v4相互之间距离为2，则它们的标号相互之间至少差2，即它们的标号应落在 I0∪I2∪I4∪I6∪I8中。又因为顶点 u0与 v0、v1、v2、v3、v4这 5 个顶点都相邻，且标号子区间 I0、I2、I4、I6、I8的长度均小于1，故f（u1）∈I1∪I3∪I5∪I7。又因顶点 u0、u1、u2、u3、u4相互之间距离为 2，若 f（u1）∈Ii，则f（u0），f（u2），f（u3），f（u4）∈[0，i-1）∪[i+2，9），其中i=1，3，5，7。

（1）若f（u1）∈I1∪I7，则f（u0），f（u2），f（u3），f（u4）∈[3，9），或f（u0），f（u2），f（u3），f（u4）∈[0，6）。因为f（u0）、f（u2）、f（u3）、f（u4）中任意2 个标号至少差2，所以它们的最大标号与最小标号的差至少为6，而区间[3，9）或[0，6）的长度小于 6，所以矛盾。

（2）若f（u1）∈I3∪I5，则f（u0），f（u2），f（u3），f（u4）∈[0，2）∪[5，9），或f（u0），f（u2），f（u3），f（u4）∈[0，4）∪[7，9）。

因为f（u0）、f（u2）、f（u3）、f（u4）中任意2 个标号至少差2，而区间[0，2）或[7，9）的长度小于2，所以f（u0）、f（u2）、f（u3）、f（u4）中至多只有 1 个标号落在区间[0，2）或[7，9）中。又因f（u0）、f（u2）、f（u3）、f（u4）中任意3 个标号的最大标号与最小标号的差至少为4，而区间[5，9）或[0，4）的长度小于4，所以矛盾。故λ1，2（H2）≥9。

综上可得，λ1，2（H2）=9。

定理3若m，n∈N 且m，n≥3，λ1，2（P2▯Pm▯Pn）=9。

证明一方面，给图P2▯Pm▯Pn定义一个标号f 如下

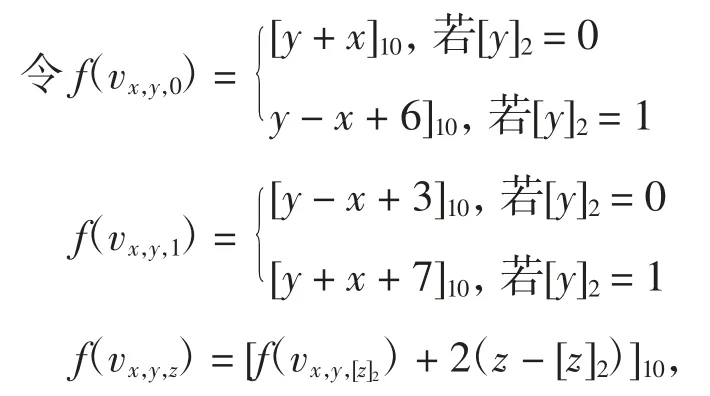
式中：x∈{0，1}；0≤y≤m-1；2≤z≤n-1。

验证 f 满足 L（1，2）-标号的条件：任取 vx，y，z∈V（P2▯Pm▯Pn），由图的对称性，与vx，y，z相邻的顶点，只需验证vx，y，z与 vx，y+1，z、v1-x，y，z、vx，y，z+1的标号差至少为 1 即可；与距离为 2 的顶点，只需验证 vx，y，z与 vx，y+2，z、v1-x，y+1，z、v1-x，y，z+1、vx，y+1，z+1、vx，y，z+2的标号差至少为 2 即可。而根据标号函数直接可知，在 vx，y+1，z、v1-x，y，z与 vx，y，z的标号差异至少为1，vx，y+2，z与 vx，y，z的标号差异至少为 2。下面利用引理 2和引理3，对其他标号进行验证。

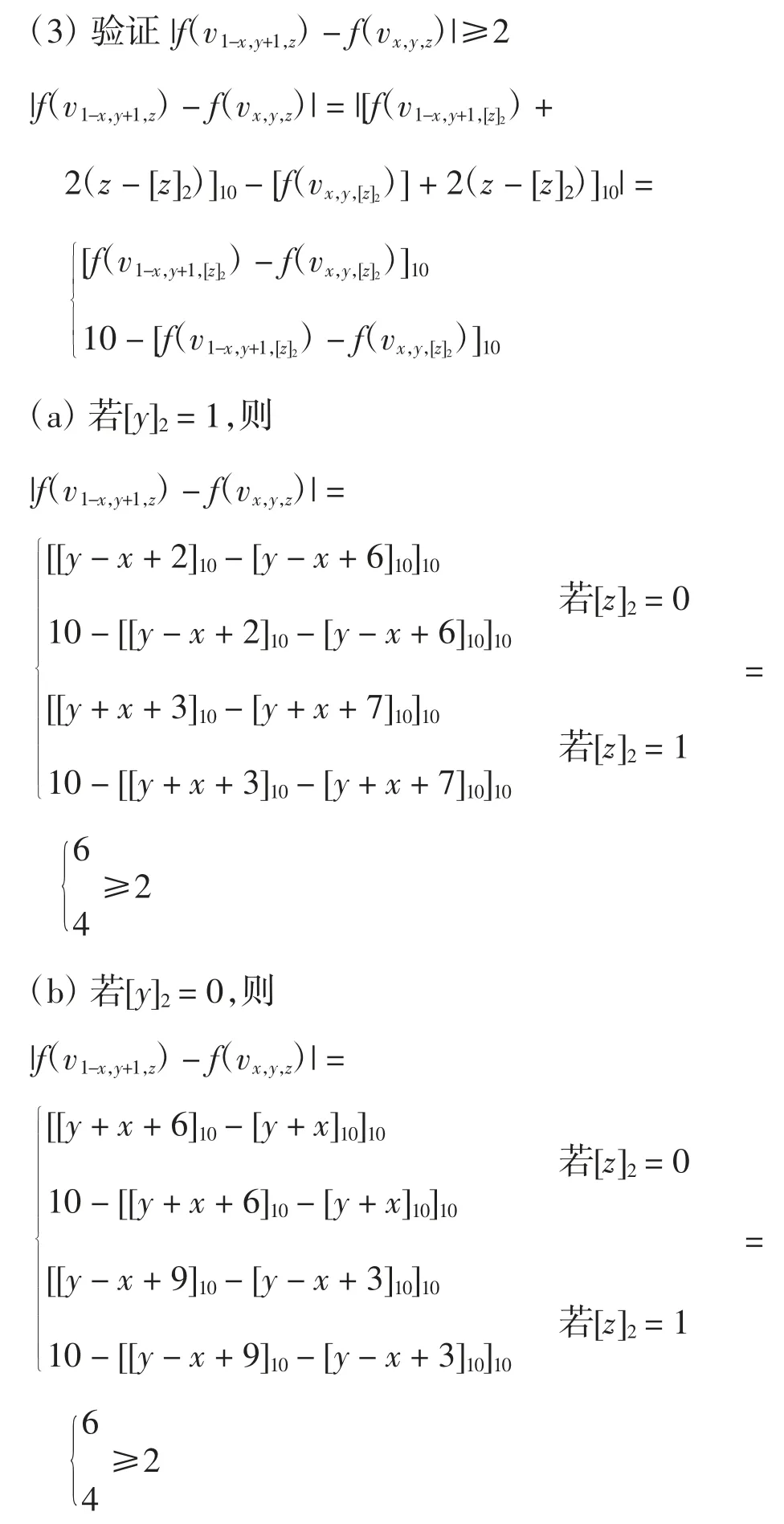
类似地，可验证|f（v1-x，y，z+1）-f（vx，y，z）|≥2，|f（vx，y+1，z+1）-f（vx，y，z）|≥2，这里不再详细列出。因此，f 满足L（1，2）-标号条件且跨度是9，即λ1，2（P2▯Pm▯Pn）≤9，这里的m，n≥3。

另一方面，由引理5 得λ1，2（H2）=9，又因H2是图P2▯Pm▯Pn的一个导出子图，由引理1 可知，λ1，2（P2▯Pm▯Pn）≥λ1，2（H2）=9，这里的m，n≥3。

综上可得，当m，n≥3 时，λ1，2（P2▯Pm▯Pn）=9。

2.2 图Pl▯Pm▯Pn 的L（1，2）-标号数

这一节主要介绍 Pl▯Pm▯Pn的 L（1，2）-标号数，这里的 l≥3，m≥3，n≥4。

引理6设图H3如图4 所示，λ1，2（H3）=11。

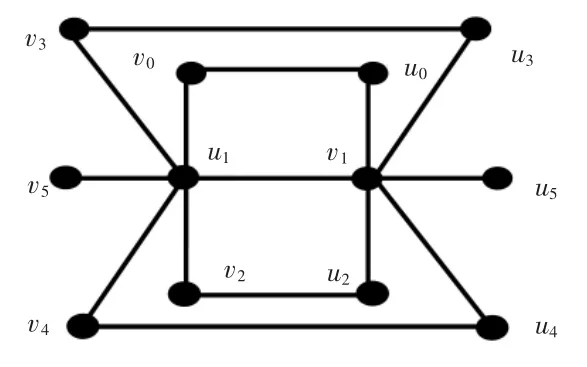
图4 图H3

证明一方面，定义f 是图H3的一个标号，标号f如下

f（v0）=0；f（v1）=2；f（v2）=4；

f（v3）=6；f（v4）=8；f（v5）=10；

f（u0）=1；f（u1）=3；f（u2）=5；

f（u3）=7；f（u4）=9；f（u5）=11。

不难验证，f 满足 L（1，2）-标号条件且跨度为 11，即λ1，2（H3）≤11。

另一方面，假设λ1，2（H3）＜11。令f 是图H3的一个 L（1，2）-标号且其中标号子区间In=[n，n+1），n=0，1，…，10。因为顶点 v0、v1、v2、v3、v4、v5相互之间距离为2，则它们的标号相互之间至少差2，即它们的标号应落在 I0∪I2∪I4∪I6∪I8∪I10。又因为顶点 u1与 v0、v1、v2、v3、v4、v5这 6 个顶点都相邻，且标号子区间I0、I2、I4、I6、I8、I10的长度均小于1，故f（u1）∈I1∪I3∪I5∪I7∪I9。又因 u0、u1、u2、u3、u4、u5相互之间距离为 2，若f（u1）∈Ii，则f（u0），f（u2），f（u3），f（u4），f（u5）∈[0，i-1）∪[i+2，11），其中 i=1，3，5，7，9。

（1）若 f（u1）∈ I1∪ I9，则 f（u0），f（u2），f（u3），f（u4），f（u5）∈[3，11），或f（u0），f（u2），f（u3），f（u4），f（u5）∈[0，8）。因为f（u0）、f（u2）、f（u3）、f（u4）、f（u5）中任意2 个标号至少差2，所以它们的最大标号与最小标号的差至少为 8，而区间[3，11）与[0，8）的长度均小于 8，所以矛盾。

（2）若f（u1）∈I3∪I7，则f（u0），f（u2），f（u3），f（u4），f（u5）∈[0，2）∪[5，11），或f（u0），f（u2），f（u3），f（u4），f（u5）∈[0，6）∪[9，11）。因为f（u0）、f（u2）、f（u3）、f（u4）、f（u5）中任意 2 个标号至少差 2，而区间[0，2）或[9，11）的长度小于2，所以至多包含f（u0）、f（u2）、f（u3）、f（u4）、f（u5）中一个标号。又因f（u0）、f（u2）、f（u3）、f（u4）、f（u5）中任意4 个标号的最大标号与最小标号的差至少为6，而区间[5，11）或[0，6）的长度均小于 6，所以矛盾。

（3）若f（u1）∈I5，则f（u0），f（u2），f（u3），f（u4），f（u5）∈[0，4）∪[7，11）。因为f（u0）、f（u2）、f（u3）、f（u4）、f（u5）中任意2 个标号至少差2，而区间[0，4）的长度小于4，所以至多包含2 个标号。又因f（u0）、f（u2）、f（u3）、f（u4）、f（u5）中任意3 个标号的最大标号与最小标号的差至少为4，而区间[7，11）的长度小于4，所以矛盾。故λ1，2（H3）≥11。

综上可得，λ1，2（H3）=11。

定理4λ1，2（P3▯P3▯P3）=10。

证明一方面，给图 P3▯P3▯P3一个标号 f 如下

f（v0，0，0）=f（v1，1，2）=0

f（v0，1，0）=f（v1，2，2）=f（v2，0，1）=1

f（v1，2，1）=10

f（v0，2，0）=f（v0，0，2）=f（v2，1，1）=2

f（v0，1，2）=f（v1，0，0）=f（v2，2，1）=3

f（v0，2，2）=f（v1，1，0）=f（v2，0，2）=4

f（v0，0，1）=f（v1，2，0）=f（v2，1，2）=5

f（v0，1，1）=f（v2，0，0）=f（v2，2，1）=6

f（v1，0，2）=f（v0，2，1）=f（v2，1，0）=7

f（v1，0，1）=f（v2，2，0）=8

f（v1，1，1）=9

不难验证，f 是图 P3▯P3▯P3的一个 L（1，2）-标号且跨度为10，即λ1，2（P3▯P3▯P3）≤10。

另一方面，因图 P3▯P3▯P3中 v1，1，2、v1，2，1、v2，1，1、v1，0，1、v0，1，1、v1，1，0是 6 个互相距离为 2 的顶点，根据 L（1，2）-标号的定义知，λ1，2（P3▯P3▯P3）≥10。综上可得，λ1，2（P3▯P3▯P3）=10。

定理5若l，m，n∈N 且l≥3，m≥3，n≥4，λ1，2（Pl▯Pm▯Pn）=11。

证明一方面，定义 f 是图 Pl▯Pm▯Pn的一个标号，标号f 如下

f（vx，y，z）=[3x+y+5z]12

式中：0≤x≤l-1；0≤y≤m-1；0≤z≤n-1。

验证f（vx，y，z）=[3x+y+5z]12满足L（1，2）-标号的条件：任取 vx，y，z∈V（Pl▯Pm▯Pn），由图的对称性，与 vx，y，z相邻的顶点，只需验证 vx，y，z与 vx，y+1，z、vx，y，z+1、vx+1，y，z的标号差至少为 1 即可；与 vx，y，z距离为 2 的顶点，只需验证的标号差至少为2 即可。

（1）验证|f（vx，y+1，z）-f（vx，y，z）|≥1 如下

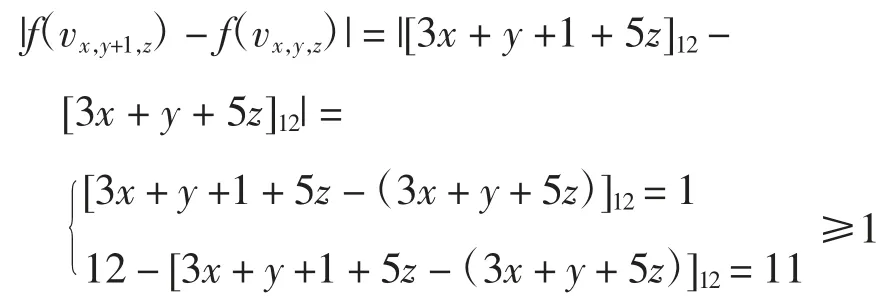
（2）验证|f（vx，y+2，z）-f（vx，y，z）|≥2 如下

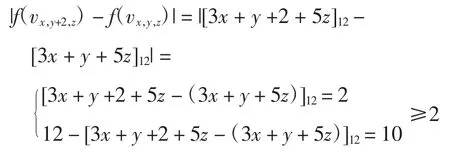
类似地，可利用引理3 对其他点标号进行验证f 满足L（1，2）-标号条件且最大跨度是11，即λ1，2（Pl▯Pm▯Pn）≤11，这里的 l≥3，m≥3，n≥4。

另一方面，由引理6 可知λ1，2（H3）= 11，又因H3是图Pl▯Pm▯Pn的一个导出子图，由引理1 可知λ1，2（Pl▯Pm▯Pn）≥λ1，2（H3）=11，这里的l≥3，m≥3，n≥4。

综上可得，当l≥3，m≥3，n≥4 时，λ1，2（Pl▯Pm▯Pn）=11。

3 结 论

本文针对三条路的笛卡尔乘积图L（1，2）-标号数展开研究，得出所有长度的三条路的笛卡尔乘积图的L（1，2）-标号数如下