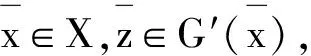集值优化问题广义近似解的性质和最优性条件*1
2015-08-18王定畅仇秋生
王定畅, 仇秋生
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
集值优化问题广义近似解的性质和最优性条件*1
王定畅, 仇秋生
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
引进了集值优化问题的一种广义近似解,统一了其他集值优化问题的近似解,研究了广义近似解的性质,获得了广义近似弱有效解的最优性条件.
集值优化;广义近似解;最优性条件;拉格朗日乘子定理
0 引 言
优化模型一般都是实际问题的简化表示.利用数值算法得到的解大多是近似解,特别在约束集非紧的情况下,有效解集(或弱有效解集)往往是空集,但近似解集在很弱的条件下都是非空的.因此,研究近似解集不仅有理论价值而且有实际意义.1979年,Kutateladz[1]首次提出了非控近似解的概念;Loridan[2]提出了拟近似解的概念.注意到近似解的集合太大,White[3]对多目标优化问题提出了5种近似有效解的概念;1995年,Tanaka[4]在赋范空间中引进了一种具有度量一致性质的近似解;1996 年,Yokoyama[5]讨论了Kutateladz,White和Tanaka意义下的近似解之间的联系;2006年,Gutierrez等[6]通过引进co-radiant集的概念定义了一个新的近似解的概念;2010 年,Gutierrez等[7]对序锥为闭凸锥的多目标优化问题引进了广义拟近似解;2012 年,高英等[8]对向量优化问题引进了一个更一般的近似有效解概念.
随着集值优化的发展,集值优化问题的近似解引起了许多学者的兴趣.1998年,陈光亚等[9]引进了集值优化问题的近似有效解;戎卫东等[10]引进了集值优化问题的近似弱有效解的概念;2011年,Gutierrez等[11]引进了更一般的G(ε)解.
综上所述,人们主要研究了向量优化问题的近似解及集值优化问题的近似有效解、近似弱有效解、近似Henig有效解,而对于集值优化问题更一般的拟近似解的研究并不多.因此,如何提出集值优化问题的拟近似解和更广义的近似解,在比较弱的条件下获得存在性定理及最优性条件,是一个值得研究的课题.本文在文献[8]的基础上,将广义近似解推广到集值优化问题,获得了更一般的近似解.
1 相关概念及引理
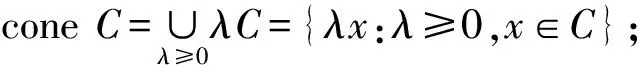
K+={l∈Y*:l(c)≥0,∀c∈C};K+i={l∈Y*:l(c)>0,∀c∈C}.
考虑下面带约束的集值优化问题:

其中:F:X→2Y;S⊂X且S≠Ø.若S=X,则(VPC)为无约束集值优化问题,记为

若无特别说明,总假设K是Y中内部非空的点凸锥,定义由K诱导出Y的偏序,即
x≤y⟸⟹y-x∈K.
2 集值优化问题的广义近似解
设G是Y中的非空子集,满足0∉clG,G∩(-K)=Ø.设φ:R+→R+为一非降的实值函数,满足φ(0)=0,φ(t)>0.记b=(G,φ).对于任意固定点x0∈X,定义集值映射φ:X→2Y,φx0(x)=φ(d(x,x0))G.
定义1[9]设ε>0,q∈K,则


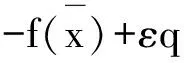
定义3[8]设f是X→Y的单值映射,ε≥0.
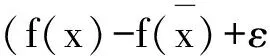
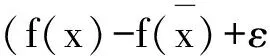
定义4设ε≥0.




注11)若取ε=0,则(VPC)相对于b的广义近似有效解和广义近似弱有效解即为集值优化问题的有效解和弱有效解.
2)若取φ(t)=1,∀t≥0,并设G∩K≠Ø,则对∀α∈G∩K,(VPC)相对于b的广义近似有效解和广义弱有效解即为定义1中的ε-有效解和ε-弱有效解.
3)设X是线性赋范空间,将F退化为单值映射,令q∈K{0},G={q},φ(d(x,y))=φ(‖x-y‖)=‖x-y‖,∀x,y∈X,则相对于b的广义近似有效解即为定义2中的拟(ε,q)-有效解.
4)若将F退化为单值映射,则(VPC)相对于b的广义近似有效解和广义近似弱有效解即为定义3中的广义ε-有效解和广义ε-弱有效解.
3 广义近似有效解和广义近似弱有效解的一些性质
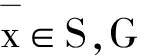
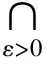
3)AE(F,K,b,ε1)⊂AE(F,K,b,ε2),∀ε2>ε1>0;
4)若G1⊂G+K,则I(F,K,b,ε)⊂I(F,K,b1,ε),∀ε>0,其中, b1=(G1,φ),I={AE,WAE};
5)若φ(t)≤φ1(t),∀t≥0,则I(F,K,b,ε)⊂I(F,K,b2,ε),∀ε>0,其中b2=(G,φ1),I={AE,WAE};
6)设b3=(G+K,φ),则I(F,K,b,ε)=I(F,K,b3,ε),其中I={AE,WAE}.
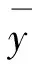

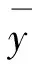

2)类似于1)的证明,故略.
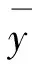

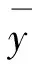
由K是凸锥知
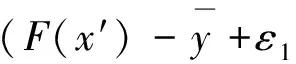
与式(2)矛盾,结论得证.
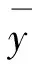

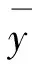
由于G1⊂G+K,故e′=e″+t,e″∈G,t∈K,代入式(4)有
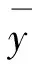
由K是凸锥知
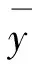
与式(3)矛盾.当I=AE,同理可证.故结论得证.
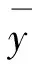

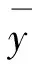

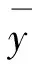
与式(5)矛盾.当I=AE时,同理可证.结论得证.
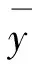

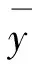

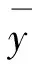

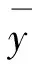
在式(7)中令t=0,有
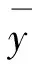
与式(8)矛盾.因此,WAE(F,K,b,ε)⊃WAE(F,K,b3,ε).类似可证当I=AE时也成立.结论得证.命题1证毕.
命题2(拓扑性质) 设X是线性度量空间,S⊂X是非空闭集,F:X→2Y上半连续.
1)若WAE(F,K,b,ε)≠Ø,则WAE(F,K,b,ε)是闭集.
2)若S为紧集,则WAE(F,K,b,ε)为紧集.


2)若S为紧集,则由1)知WAE(F,K,b,ε)是闭集,故易知WAE(F,K,b,ε)为紧集.
3)任取WEE(F,K,b,ε)中收敛的网{(xα,yα)}α∈I, 记(xα,yα)→(x0,y0).由S是闭集知x0∈S.
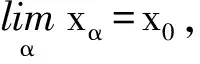
再证(x0,y0)∈WEE(F,K,b,ε).若不然,则对上述y0,存在x′∈S,e∈G,y′∈F(x′), 使得y′-y0+εφ(d(x′,x0))e∈-intK.
由φ的连续性知y′-yα+εφ(d(x′,xα))e→y′-y0+εφ(d(x′,x0))e,且-intK是开集,与(xα,yα)∈WEE(F,K,b,ε)矛盾.因此,(x0,y0)∈WEE(F,K,b,ε),即WEE(F,K,b,ε)是闭集.命题2证毕.
4 广义近似解的最优性条件
对集值映射F:X→2Y,若∀x,y∈X,λ∈[0,1], 有λF(x)+(1-λ)F(y)⊂F(λx+(1-λ)y)+K,则称集值映射F为凸的
注2易知若集值映射F:X→2Y为凸的,从而F(X)+K为凸集.
命题3设X是Banach空间,G⊂K是凸集,F是凸的,且φ是正齐次次可加的.任取x0∈X,定义集值映射φx0(x)=φ(d(x,x0))G.则F+εφx0是凸集值映射.
证明 任取x1,x2∈X,y1∈F(x1),y2∈F(x2),e1,e2∈G,λ∈(0,1).由φ正齐次和次可加知
λφ(d(x1,x0))+(1-λ)φ(d(x2,x0))≥φ(d(λx1+(1-λ)x2,x0)).
下证
y1+(1-λ)y2+λφ(d(x1,x0))e1+(1-λ)φ(d(x2,x0))e2∈F(λx1+(1-λ)x2)+
εφx0(λx1+(1-λ)x2)+K.
由题意知,
λφ(d(x1,x0))e1+(1-λ)φ(d(x2,x0))e2=(λφ(d(x1,x0))+(1-λ)φ(d(x2,x0)))e3.

λy1+(1-λ)y2+λφ(d(x1,x0))e1+(1-λ)φ(d(x2,x0))e2=
λy1+(1-λ)y2+(λφ(d(x1,x0))+(1-λ)φ(d(x2,x0)))e3=
λy1+(1-λ)y2+(φ(d(λx1+(1-λx2),x0)))e3+(λφ(d(x1,x0))+(1-λ)φ(d(x2,x0))-
φ(d(λx1+(1-λx2),x0)))e3∈F(λx1+(1-λ)x2)+εφx0(λx1+(1-λ)x2)+K,
即得F+εφx0是凸集值映射.命题3证毕.
定理1(择一性定理) 设X是Banach空间,G⊂K是凸集,F是凸的,且φ是正齐次次可加的,则以下结论有且仅有一个成立:
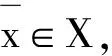
2)存在l∈K+{0},使得l(y0)≤l(y)+εφ(d(x,x0))l(e),∀x∈X,y∈F(x),e∈G.
证明 易知若1)成立,则2)不成立.下证若1)不成立,则2)成立,即对∀x∈X,(F(x)-y0+εφx0(x))∩(-intK)=Ø.由K是凸锥知(F(X)-y0+εφx0(X)+K)∩(-intK)=Ø.又由命题3和注2知F(X)+εφx0(X)+K是凸集.由凸集分离定理知,存在l∈Y*{0},使得

下证l∈K+{0}.若不然,则存在c0∈K,使得l(c0)<0.由K是凸锥知,固定y,q,e,∀λ>0,有

在式(10)中令λ→+∞,即得l(-q)=-∞,矛盾.故l∈K+{0}.在式(9)中令c→0,q→0,得
l(y0)≤l(y)+εφ(d(x,x0))l(e), ∀x∈X,y∈F(x),e∈G.
因此,2)成立.定理1证毕.
定理2设定理1中的条件均满足,则(x0,y0)是(VP)问题关于b的广义近似弱有效元当且仅当存在l∈K+{0},使得

证明 若(x0,y0)是(VP)关于b的广义近似弱有效元,则由定理1知存在l∈K+{0},使得

又由y0∈F(x0)+εφx0(x0)知式(12)的右端可达到下确界,即
inf{l(z) :z∈F(x)+εφx0(x),x∈X}=l(y0).
反之,若存在l∈K+{0},使得
inf{l(z) :z∈F(x)+εφx0(x),x∈X}=l(y0).
而(x0,y0)不是(VP)关于b 的广义近似弱有效解.因此,对上述y0,存在x′∈X,y′∈F(x′),e′∈G,使得y′-y0+εφ(d(x′,x0))e′∈-intK,故l(y′)+εφ(d(x′,x0))l(e′) 设Z是拓扑向量空间,G′:X→2Z是一集值映射,D为Z中的一内部非空的凸锥,K内部非空.记B(Z,Y)为Z→Y的所有连续线性算子,B+={s∈B(Z,Y) : s(D)⊂K}.现考虑集值优化问题 其中,A={x∈X : G′(x)∩(-D)≠Ø}. 定理3设: 1)(x0,y0)是(VP)关于b的广义近似弱有效元; 2)G′(X)∩(-intD)≠Ø; 3)F+εφx0和G′是凸集值映射. 则存在s∈B+(Z,Y),使得(x0,y0)是以下问题关于b的广义近似弱有效元: (LP) {minF(x)+s(G′(x))+εφx0(x) : x∈X}. 且存在z0∈G′(x0),使得s(z0)=0. 证明 由于(x0,y0)是(VP)关于b的广义近似弱有效元,故对∀x∈A,有 (F(x)-y0+εφ(d(x,x0))G)∩(-intK)=Ø. 而∀x∉A,G′(x)∩(-D)=Ø,故 ((F-y0+εφx0)(X),G′(X))∩(-intK,-intD)=Ø. 又由(F+εφx0,G′)是凸集值映射知((F-y0+εφx0)(X)+K,G′(X)+D)是凸集,且 ((F-y0+εφx0)(X)+K,G′(X)+D)∩(-intK,-intD)=Ø. 由定理1知存在(η,l)∈(K+,D+){0,0},使得 由G′(x0)∩(-D)≠Ø知,可任取z0∈G′(x0)∩(-D).令x=x0,y=y0,z=z0,代入式(13)得l(z0)≥0.又由l∈D+,z0∈-D知l(z0)≤0.因此,l(z0)=0. 由K内部非空知可取c∈K,l(c)=1.定义s(z)=l(z)c,∀z∈Z.易知s是Z→Y的连续线性算子,且满足s(D)=l(D)c⊂K.因此,s∈B+(Z,Y).由s(z0)=l(z0)c=0,∀z0∈G′(x0)∩(-D),可得0∈s(G′(x0)),故 y0∈F(x0)⊂F(x0)+s(G′(x0))+εφx0⊂F(X)+s(G′(X))+εφx0(X). 对∀x∈X,y∈F(x),z∈G′(x),e∈G,有 下证(x0,y0)是(LP)问题相对于b的广义近似弱有效元.反证,若不然,则对上述y0,存在x′∈X,y′∈F(x′),e′∈G,z′∈G′(x′),使得 (y′-s(z′)+εφ(d(x′,x0))e′-y0)∩(-intK)≠Ø. 因此,η(y0)>η(y′)+l(z′)+εφ(d(x′,x0))η(e′).与式(14)矛盾.定理3证毕. [1]Kuatateladze S S.Convexε-programing[J].Sov Math Dokl,1979,20(2):391-393. [2]Lordian P.ε-solution in vector minimization problem[J].J Optim Theory Appl,1984,43(2):265-272. [3]White D J.Epsilon efficiency[J].J Optim Theory Appl,1986,49(2):319-337. [4]Tanaka T.A new approach to approximation of solutions in vector optimization problems[C]//Fushimi M T.Proceedings of APORS.Singapore:World Scientific,1995:497-504. [5]Yokoyama K.Epsilon approximate solutions for multiobjective programming problems[J].J Math Anal Appl,1996,203(1):497-504. [6]Gutierrez C,Jimenez B,Novo V.A unified approach and optimality conditions for approximate solutions of vector optimization problems[J].SIAM J Optim Theory Appl,2006,17(3):688-710. [7]Gutierrez C,Lopez V,Novo V.Generalized quasi-solutions in multioblective optimization problems:Existence result and optimality conditions[J].Nonlinear Anal,2010,72(11):97-120. [8]Gao Y,Hou S H,Yang X M.Existence and optimality conditions for approximate solutions to vector optimization problems[J].J Optim Theory Appl,2012,152(1):97-120. [9]Chen Guangya,Huang X X.Ekeland′sε-variational principle for set-valued mappings[J].Math Method Oper Res,1998,48(1):181-186. [10]Rong W D,Wu Y N.ε-weak minimal solutions for vector optimization problems with set-valued maps[J].J Optim Theory Appl,2000,106(3):569-579. [11]Gutierrez C,Jimenez B,Novo V.A generic approach to approximate efficiency and applications to vector optimization with set-valued maps[J].J Global Optim,2011,49(2):313-342. [12]Beldiman M,Panaitescu E,Dogaru L.Approximate quasi efficient solutions in multiobjective optimization[J].Bull Math Soc Sci Math Roum,2008,99(2):109-121. (责任编辑 陶立方) Thepropertiesandoptimalityconditionsforgeneralizedapproximatesolutionstoset-valuedoptimizationproblems WANG Dingchang, QIU Qiusheng (CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China) A new concept of generalized approximate solution to set-valued optimization problems was introduced in order to unify the other apprximate solutions which had been inverstigated before. Some properties of generalized approximate solution were studied, and the optimality conditions for generalized approximate weak efficient solution were proposed. set-valued optimization; generalized approximate solution; optimality condition; Lagrange multiplier theorem 10.16218/j.issn.1001-5051.2015.02.006 2014-05-11 国家自然科学基金资助项目(11471291) 王定畅(1989-),男,浙江兰溪人,硕士研究生.研究方向:最优化理论. 仇秋生.E-mail: qsqiu@zjnu.cn O221.6 A 1001-5051(2015)02-0156-075 拉格朗日乘子定理