电镀电源控制算法的研究与仿真应用
2015-08-14顾蓉王宝忠刘浪
顾蓉+王宝忠+刘浪


摘 要: 在直流电镀工艺需要电源输出电流调节范围宽、输出电流值稳定的背景下,针对PID参数整定困难,积分分离的增量式PID阈值选定困难,智能算法结构复杂、不易实现这几个问题,首先改进了PID算法,然后将最小二乘法应用在PID参数整定中,最后将改进的PID算法应用在电镀电源的控制中,实现了对系统的精密控制。改进的PID算法结构简单,参数易于整定,阈值易于选取,仿真结果表明,改进的PID算法在电镀电源控制中取得了良好的效果。
关键词: 增量式PID; PID参数整定; 最小二乘法; 电镀电源
中图分类号: TN05?34; TP301.6 文献标识码: A 文章编号: 1004?373X(2015)15?0145?04
Research on electroplating power supply control algorithm and its simulation applications
GU Rong, WANG Baozhong, LIU Lang
(School of Electronics and Information, Jiangsu University of Science and Technology, Zhenjiang 212003, China)
Abstract: DC electroplating technique needs power supply output wide adjustment range current and stable current value. Under this background, the PID algorithm is improved because it is difficult to tune PID parameter, hard to choose integral se?parated incremental PID threshold, and intelligent algorithm has complex structure and is difficult to implement. Then the least square method is applied in PID parameter tuning. Then the improved PID algorithm is applied in electroplating power control, and the precise control to the system is achieved. The improved PID algorithm has the advantages of simple structure, easy to tuning, liable to select the threshold. The simulation results show that the improved PID algorithm has achieved good results in electroplating power supply control.
Keywords: incremental PID; PID parameter tuning; least square method; electroplating power supply
0 引 言
影响电镀质量的因素包括:阳极材料的质量、电镀液的成分、温度、通电时间、搅拌强度、析出的杂质、电流参数等[1],其中电源是电镀最主要的设备。不同的电镀工艺对电源的要求是不一样的,如镀铜,采用脉动直流电能提高镀层光亮度;相反,对于镀铬,就只能用直流电才能得到良好的镀层,如果有交流成份,铬镀层的亮度会降低,甚至发白,发雾,变灰,直流中所含的交流成份越大,这种现象就越严重。除用得很少的铝件交流氧化直接用可调低压交流电外,其他基本上都采用直流电源。任何镀液都有一个获得良好镀层的电流密度范围,获得良好镀层的最大电流密度称为电流密度上限,获得良好镀层的最小电流密度称为电流密度下限,这就要求电源的输出电流从开机开始迅速达到设定值并保持稳定,纹波系数小。使用符合要求的直流电源是精密电镀的基本要求。据此,对电镀电源的控制算法进行研究,以使电源响应速度快、纹波系数低、电流调节范围宽、稳定可靠。电镀电源的目标输出电流波形如图1所示。
图1 目标电流波形
1 系统仿真模型
利用Matlab/Simulink建立仿真模型如图2所示。
1.1 控制算法
PID控制器是目前应用最为广泛的一种控制器,它利用受控系统的输入输出数据来设计,结构简单,使用方便[2],因此本文拟采用PID算法控制电镀电源。PID算法原理框图如图3所示。
图2 电镀电源Matlab仿真模型
图3 PID控制系统原理框图
增量式PID算法是对PID算法公式进行变换得到的,由于增量式PID算法具有计算量小,易于实现的优点,所以首先采用增量式PID算法。
1.2 增量式PID算法
增量式PID算法中控制器的输出是系统控制量的增量[Δuk。]当系统的执行机构所需的不是控制量本身,而是控制量的增量时,应该使用增量式PID算法对系统进行控制。增量式PID的控制规律如下:
[Δuk=kp[e(k)-e(k-1)]+kie(k)+kd[e(k)-2e(k-1)+e(k-2)]] (1)
将增量式PID应用到系统中,设定值为4 000,得出仿真图如图4所示。
图4 增量式PID调节图
PID算法中的积分环节主要作用是消除静差,但如果积分作用参与了系统调节的整个过程,由于起始阶段系统偏差较大,很容易造成积分饱和,导致PID公式的运算结果超过执行机构的最大控制量,使系统输出量存在较大的超调,甚至引起大的振荡[3],如图4所示。这样的电源存在诸如响应不够快、超调、稳定性不够好等问题,这样的电源应用在电镀生产中势必会影响产品质量。为改善超调和振荡问题,将积分作用从PID算法中分离出来,即改为采用增量式积分分离PID算法。
1.3 增量式积分分离PID控制算法
积分分离的具体做法是:当系统的输出误差较大时,积分作用不参与调节;当系统的输出误差较小时,加入积分控制来消除静差。其具体实现步骤如下[4]:
(1) 根据实际情况,人为设定阈值[ε>0];
(2) 当[error(k)>ε]时,采用PD控制;
(3) 当[error(k)≤ε]时,采用PID控制。
增量式积分分离控制算法可表示为:
[Δuk=kp[e(k)-e(k-1)]+βkie(k)+kd[e(k)-2e(k-1)+e(k-2)]]
(2)
其中[β]为积分项的开关系数。
[β=1,error(k)≤ε0,error(k)>ε] (3)
将增量式积分分离PID算法应用到系统中,仿真得到如图5,图6所示波形,这两幅图为阈值分别是300和100,给定值分别为4 000和600时系统的输出电流波形。
图5 给定值为4 000时输出电流波形
图6 给定值为600时输出电流波形
由仿真图可知,增量式积分分离PID控制算法一定程度上解决了增量式PID算法中的超调和振荡问题,如图5中阈值为300时的情形,但是由于电镀电源输出电流大,调节范围宽,阈值设定就成了一个比较棘手的问题,对于小的设定值,阈值过大,达不到积分分离的目的,如图6所示,阈值为300时系统存在超调;对于大的设定值,阈值设定过小,系统可能进不了积分作用区间,会出现较大的残差,如图5所示,阈值为100时系统存在较大的静差,大约为200。仿真结果表明,对于调节范围宽的电镀电源系统,增量式积分分离PID控制算法不能兼顾各设定值下的系统输出电流波形。为了解决系统由于阈值选择不当而出现的超调或静差问题,拟改进增量式积分分离PID控制算法。
1.4 改进的增量式积分分离PID算法
即使是对于同一个系统,不同的输出值所允许的误差绝对值都是不一样的,系统通常会规定一个允许的误差百分比,即要求误差和设定值的比值在允许的范围内,据此,本文将系统给定值[r]引入算法,利用误差[error(k)]和给定值[r]的比值作为开关系数的判断条件,将误差和给定值的比值叫做误差百分比,改进的增量式积分分离PID算法具体实现步骤如下:
(1) 根据系统允许的误差百分比设定阈值[ε>0];
(2) 当[error(k)r>ε]时,采用PD控制;
(3) 当[error(k)r≤ε]时,采用PID控制。
改进的积分分离PID控制算法公式和增量式积分分离PID算法的公式无异,不同点在于开关系数的判断条件变为:
[β=1,error(k)r≤ε0,error(k)r>ε] (4)
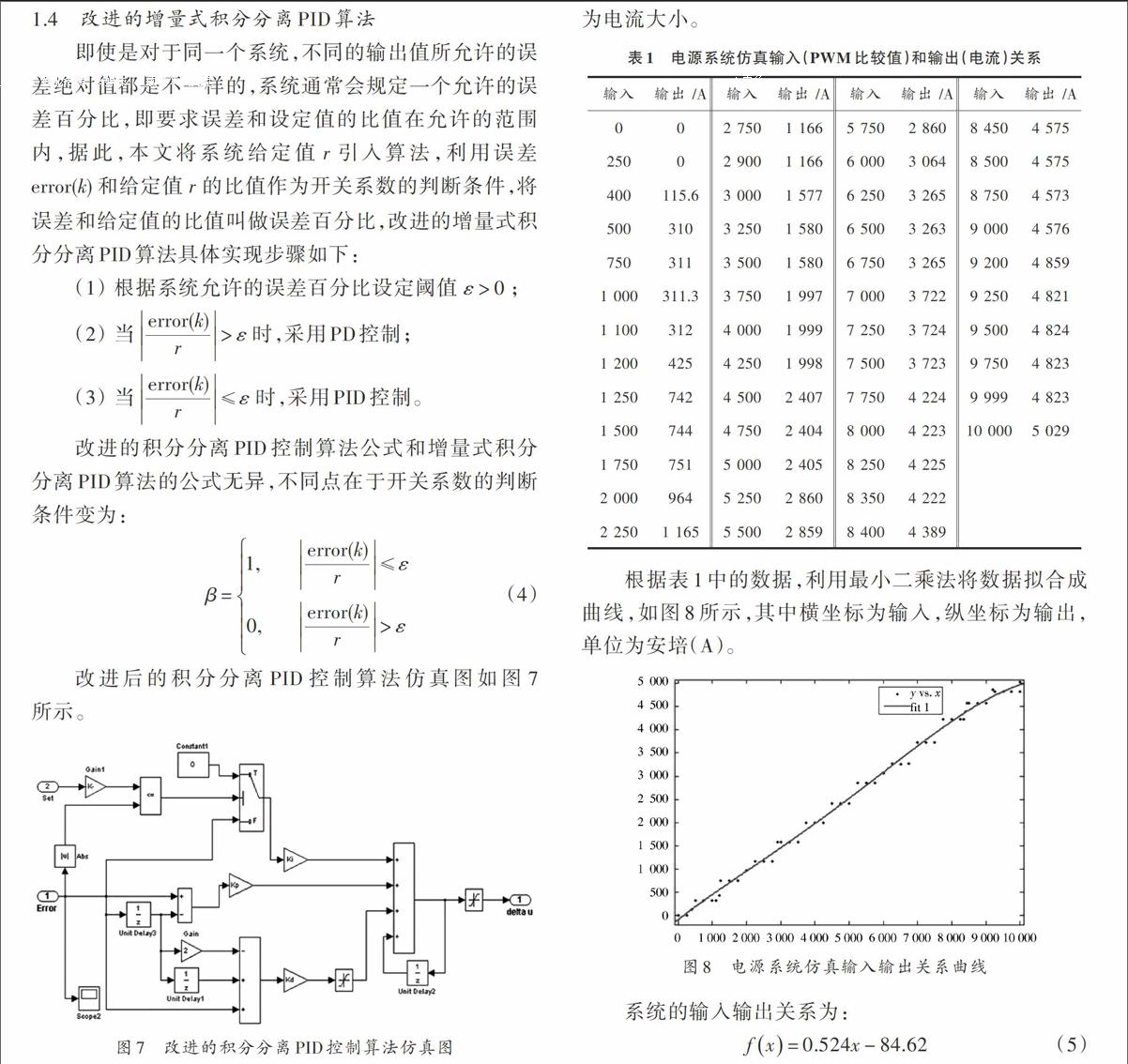
改进后的积分分离PID控制算法仿真图如图7所示。
图7 改进的积分分离PID控制算法仿真图
2 PID参数整定
PID算法的三个参数是应用该算法的重点和难点,它们共同决定系统最终的控制效果[5]。工程上,PID控制器的参数常常是通过试凑,或者通过实验经验来确定。这些方法不仅耗时,还依赖专家经验。利用Matlab可以在系统投入运行前对系统进行仿真,在此基础上,虽然不能准确建立系统的数学模型,但是可以降低系统的不确定性[6]。要了解系统,首先要了解系统的输入输出关系。通过对系统进行仿真得出了一组输入输出数据,如表1所示。系统的输入为PWM波的比较值,输出为电流大小。
表1 电源系统仿真输入(PWM比较值)和输出(电流)关系
[输入\&输出 /A\&输入\&输出 /A\&输入\&输出 /A\&输入\&输出 /A\&0\&0\&2 750\&1 166\&5 750\&2 860\&8 450\&4 575\&250\&0\&2 900\&1 166\&6 000\&3 064\&8 500\&4 575\&400\&115.6\&3 000\&1 577\&6 250\&3 265\&8 750\&4 573\&500\&310\&3 250\&1 580\&6 500\&3 263\&9 000\&4 576\&750\&311\&3 500\&1 580\&6 750\&3 265\&9 200\&4 859\&1 000\&311.3\&3 750\&1 997\&7 000\&3 722\&9 250\&4 821\&1 100\&312\&4 000\&1 999\&7 250\&3 724\&9 500\&4 824\&1 200\&425\&4 250\&1 998\&7 500\&3 723\&9 750\&4 823\&1 250\&742\&4 500\&2 407\&7 750\&4 224\&9 999\&4 823\&1 500\&744\&4 750\&2 404\&8 000\&4 223\&10 000\&5 029\&1 750\&751\&5 000\&2 405\&8 250\&4 225\&\&\&2 000\&964\&5 250\&2 860\&8 350\&4 222\&\&\&2 250\&1 165\&5 500\&2 859\&8 400\&4 389\&\&\&]
根据表1中的数据,利用最小二乘法将数据拟合成曲线,如图8所示,其中横坐标为输入,纵坐标为输出,单位为安培(A)。
图8 电源系统仿真输入输出关系曲线
系统的输入输出关系为:
[fx=0.524x-84.62] (5)
在系统中输入为控制算法的计算结果,输出为系统的稳定值。首先整定比例系数,为方便比例参数整定,将拟合曲线的方程式简化为[fx=0.5x。]仅在比例作用下,比例系数[Kp]和系统的稳定值[m]的关系为:
[m=Kpr-m×0.5]
仅在比例作用下,系统最终存在静差,值为[r-m,]将该静差取为给定值的1%,即系统仅在比例作用下最终输出电流达到给定值的99%,[m=]99%[r,]经计算得[Kp=198,][Kp]取200。这样仅在比例作用下,系统最终大致会稳定在99%[r]处。当系统的输出值达到给定值的[99%]时,即在[error(k)r≤]1%时,加入积分调节,由于开关电源是一个非线性系统,即便经过计算,但在比例作用下系统输出值也还并不十分确定,因此阈值要留有一定的裕量,因此取阈值为1.5%,即[ε=0.015。]由于积分作用受到了限制,积分参数的整定变得相对容易,由于比例作用下系统的静差很小,经试验,[Ki]取各数量级的值均能达到良好的控制效果,其中[Ki]取1效果最佳。最后整定微分系数,由于微分作用的存在,系统可能会出现较大的波动,于是给微分作用进行限幅,经整定,[Kd]取1最为合适[7]。
3 仿真结果及分析
首先将给定值设为2 000,调节给定值到4 000,再调节到3 000,系统仿真结果如图9及图10所示,其中图10为图9的细节图。
图9 改进的PID算法仿真结果
图10 仿真结果细节图
从仿真结果可以看出,应用改进算法的PID,系统对于各给定值既无超调也无静差,只是在稳定值附近有微小波动,和增量式积分分离PID算法相比,该系统阈值的选取容易很多。
以模糊算法为例,将改进的PID算法与模糊自适应PID算法分别应用到电镀电源系统中,并对效果进行比较[6]。图11为改进的PID算法控制效果与模糊自适应PID算法的控制效果对比图,给定值均为4 000。图12为系统稳定后放大的输出电流图。
图11 改进的PID算法控制与模糊PID算法控制对比
图12 放大的输出电流图
如图11,图12所示,系统采用改进的PID算法时,稳定时间约为0.006 s,稳定后波动约为±3,纹波系数<1‰,采用模糊自适应PID算法时,稳定时间约为0.02 s,稳定后波动约为±4;和采用模糊PID算法的系统相比,采用改进的PID算法系统响应更迅速,运行更稳定。且一般模糊逻辑系统的设计存在两个棘手的问题:一是隶属函数个数、形状的确定及其坐标位置的调节;二是模糊规则的确定[8?9],设计过程较复杂。相比来说,改进的PID算法结构简单,易于实现和应用。
4 结 语
综上所述,改进的增量式积分分离PID算法结构简单,易于实现;PID参数易于整定;阈值选取简单;纹波系数低;不必采用智能算法,省去了规则的制定,减少了系统的运算量,系统响应更快。采用改进后的PID算法,由于系统反应速度快(毫秒级),对于网电及负载变化具有极强的适应性,输出误差大约为0.1%,电源的控制精度高,电流稳定,对于使用直流电镀工艺的产品,有利于提高产品质量[10]。
在后续的工作中,将在系统中加入智能学习算法,自学习系统的输入输出关系,利用学习到的信息来整定PID参数,智能化地提高PID算法对系统的控制效果,实现系统的全面智能精确控制。
参考文献
[1] DATTA M. Electrochemical processing technologies in chip fabrication: challenges and opportunities [J]. Electrochimica Acta, 2003, 2(48): 2975? 2985.
[2] 晏静文,侯忠生.学习增强型PID控制系统的收敛性分析[J].控制理论与应用,2010,27(6):761?768.
[3] 刘金琨.先进PID控制Matlab仿真[M].3版.北京:电子工业出版社,2013.
[4] 傅信.过程计算机控制系统[M].西安:西北工业大学出版社,1995.
[5] 何佳佳,侯在恩.PID参数优化算法[J].化工自动化及仪表,2010,37(11):1?4.
[6] 王素青,姜维福.基于Matlab/Simulink的PID参数整定[J].自动化技术与应用,2009,28(3):24?28.
[7] 曾豪勇,周思柱,易文君.基于Matlab的增量式PID参数整定[J].工业控制计算机,2014(6):69?70.
[8] 艾学忠,金炳涛.具有安全监管的锂电池矿灯智能充电技术的研究[J].化工自动化及仪表,2010,37(2):100?101.
[9] 艾学忠,金炳涛,柳仁禹.精密智能电镀电源的设计[J].吉林化工学院学报,2013,30(11):76?78.
[10] 付瑞玲,乐丽琴.基于Matlab/Simulink的PID参数整定[J].工业控制计算机,2013,26(8):75?76.
